基于动态分级蝴蝶优化算法的WSN 节点覆盖优化*

吴 亮赵晴峰汤显峰

(1.中国科学院大学附属肿瘤医院(浙江省肿瘤医院)，浙江 杭州310022；2.中国科学院基础医学与肿瘤研究所，浙江 杭州310022；3.浙江大学信息技术中心，浙江 杭州310027)

无线传感器网络(Wireless Sensor Network，WSN)具有成本低、覆盖范围广、布署灵活的特点[1]，已经被广泛应用于环境监测、智慧交通、健康医疗等诸多领域[2-4]。 而监测区域内传感器节点分布是否均匀、是否具有高覆盖率成为决定影响无线传感器网络监测质量和网络生存时间的关键因素。若将大量传感器节点在区域内随机布署，容易出现节点聚集、覆盖盲区等问题。 若局部区域节点密度过高，不仅会产生过多的冗余数据传输和网络拥塞，还会导致过多的能量浪费。 而覆盖盲区则会降低区域的监测质量，影响网络的可靠性。 因此，优化传感器节点的布署和覆盖，以均衡的能耗要求，以尽可能少的布署节点完成高区域覆盖率对无线传感器网络的发展将具有重要的现实意义。

群智能优化算法因其强大的启发式搜索思维和全局搜索能力，近年来已被广泛应用于传感器节点的覆盖优化问题。 文献[5]针对不均匀问题提出了改进自适应粒子群(Improved Particle Swarm Optimization，IPSO)的节点覆盖优化算法，通过进化因子和聚合因子对惯性权重的改进，提升了传统粒子群的寻优性能，将网络覆盖率提高了2%～6%。 文献[6]设计了一种混沌优化细菌觅食算法(Chaos Optimization of Bacterial Foraging Algorithm，COBFA)对节点布署进行优化，构造了多目标优化模型，提高了覆盖率和网络综合利用率。 文献[7]设计基于虚拟力的改进粒子群优化算法(Virtual Force Particle Swarm Optimization，VFPSO)，引入维度选择策略，将传感节点布署后的覆盖率提升了约5%。 文献[8]设计了自适应动态混沌量子粒子群算法(Dynamic self-Adaptive Chaotic Quantum-behaved PSO，DACQPSO)，利用种群分布熵和平均粒距的概念，加速了量子粒子群的进化寻优过程，平均覆盖率提高了约2.7%，但依然存在覆盖盲区。 文献[9]提出了改进灰狼优化算法(Improved Grey Wolf Optimization，IGWO)，利用混沌机制、收敛因子非线性调节及混合变异对传统GWO 算法进行改进，网络覆盖率提升了3%，但仍存在部分区域布署过于集中、分布缺乏均匀性的问题。 文献[10]针对分布不均匀的低覆盖率问题，提出了改进鲸鱼优化(Improved Whale Optimization Algorithm，IWOA)的覆盖优化算法，最后以更少的传感节点布署得到更高的覆盖率，网络监测质量有所提高。 上述算法在优化传感器节点覆盖问题上虽然取得了性能提升，但群智能优化算法本身所固有的寻优精度不高、收敛速度慢、易于早熟收敛等问题还有待进一步解决，这使得在提高网络覆盖率、均衡节点能量使用等问题上仍然有进一步的优化空间。

蝴蝶优化算法(Butterfly Optimization Algorithm，BOA)是2019年提出的一种模拟蝴蝶种群觅食行为的智能优化算法[11]。 该算法易于实现，依赖参数少。 在求解高维度函数优化问题时，其性能已经优于传统粒子群算法(Particle Swarm Optimization，PSO)、差分进化算法(Differential Evolution，DE)和蜂群优化算法(Artificial Bee Colony，ABC)。 因此，已经广泛应用于特征选择[12]、图像分割[13]和工程设计优化[14]等问题。 然而，标准BOA 算法依然存在寻优精度低、收敛速度慢的不足，尤其在解决高维复杂问题时，算法的寻优稳定性、跳离局部最优能力的适应性依然还有很大改进空间。

为了更好地进行传感器节点的覆盖优化，提升传感器节点能量的均衡利用，本文设计了一种基于动态分级的改进蝴蝶优化算法(Dynamic Leveling Butterfly Optimization Algorithm，DLBOA)。 为了提高传统蝴蝶优化算法的寻优性能，通过混沌映射优化初始种群结构，提升种群多样性；设计动态分级策略，基于种群个体适应度，将种群划分为差、中、优三种等级，并分别利用黄金正弦算法、惯性权重位置更新和精英引导机制进行优化，以提高算法的收敛速度，增强脱离局部最优的能力。 将DLBOA 算法应用于求解WSN 中传感器节点的覆盖优化问题。 结果表明，改进算法实现了预期效果，在提升区域覆盖率和均衡能量利用方面具有明显效果。

1 模型描述

1.1 WSN 覆盖模型

将若干同质结构的传感器节点布署于规则的二维平面区域，布署后的传感节点不具备移动性。 同时，传感器节点可以感知在其感知半径以内的其他节点。 令无线传感器网络WSN 的节点布署区域大小S=L×M，单位:m2，可将其视为L×M的网格，单个网格大小为1，则区域内可监测的像素点数为L×M。令集合Z={Z1，Z2，…，ZV}表示待布署的传感器节点集合，节点总数为V。 令r为节点的感知半径，R为数据通信半径，且r≤2R。

假设传感器Zi的坐标位置为(xi，yi)，i=1，2，…，V，(xj，yj)为区域内某像素点gj的坐标，则传感器Zi与像素点gj的距离为:

若d(Zi，gj)≤r，则表明像素点gj可被传感器节点Zi感知并覆盖。 则可以通过布尔0-1 测量模型定义节点感知模型，定义点gj被传感节点Zi感知的概率为:

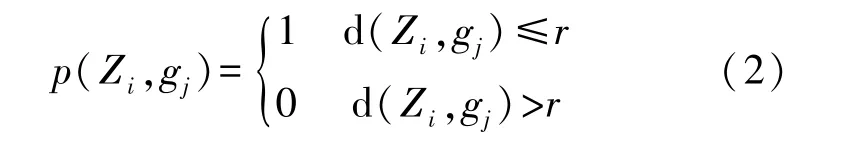
通常情况下，一个传感器节点可以被多个节点同时感知。 因此，为了提升无线传感器布署区域的感知概率，像素点gj被布署的传感器节点联合感知的概率可定义为:

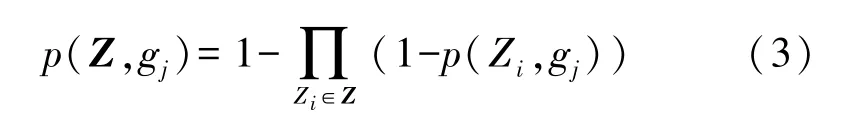
则网络整体覆盖率为所有传感器节点所覆盖的目标像素点数量与布署区域内的总像素点数量之比[9]，为:

1.2 能耗模型

传感器节点能耗主要由节点进行数据收发时的能耗组成，能耗模型如图1 所示。 功率放大器根据收发双方间距决定使用Friss 自由空间模型或者多路衰减模型。 令传感器节点间距为dis，数据发送量为lbit，则节点的发送能耗计算为[6]:

图1 传感器节点的能耗模型

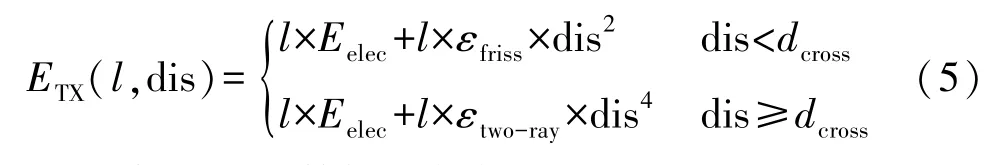
接收lbit 数据的能耗为:

式中:Eelec为射频电路/接收电路单位bit 数据的能耗，εfriss、εtwo-ray为自由空间模型和多路衰减模型中功率放大器的能耗，dcross为能耗模型距离阈值。

若令传感器节点的初始能量为Estart，则经过数据发送与接收后，其剩余能量为:

式中:α、β分别表示传感器节点发送与接收数据的次数。

1.3 目标函数

无线传感器网络WSN 中的节点覆盖优化问题，是以更少的传感器节点布署数量，在确保能耗均衡的前提下，尽可能得到更高的区域覆盖率。 将目标函数定义为:

式中:F1=COV(Z)，表示网络覆盖率；F2=(V-V′)/V，表示传感节点空闲率；F3为剩余能量均衡函数，定义为:

式中:Ei为目标节点所在局部区域的传感器剩余能量，E′i为传感节点剩余能量之和，W为感知像素点周围的传感节点数。w1、w2、w3分别表示网络覆盖率权重、传感节点节省权重和传感节点剩余能量权重，用于定义对目标的偏好程度，且w1＋w2＋w3=1。

2 BOA 算法

BOA 算法中，每只蝴蝶会散发一定浓度的香味，经过空气扩散后，其他个体会根据香味浓度被其吸引。 若嗅到最高浓度的香味，个体会向其靠近，该过程即为全局搜索。 若感知不到任何香味，个体将在空间内进行随机游走式飞行，该过程即为局部开发。 香味浓度的计算公式为:

式中:I为刺激强度，c为感知形态，a为幂指数，理解为不同程度香味的吸收，且a、c∈[0，1]，BOA 算法中，通常a= 0.1，c初值为0.01，其迭代变化公式为:

式中:Tmax为最大迭代次数。

蝴蝶个体全局搜索时的位置更新方式为:

式中:xi(t)为原始位置，xi＋1(t＋1)为迭代后的新位置，g*为当前最优位置(解)，r1∈[0，1]，为随机量，fi为蝴蝶i的香味浓度。

蝴蝶个体局部开发时的位置更新方式为:

式中:xj(t)、xk(t)为种群中随机选择的两只蝴蝶的位置，r2∈[0，1]，为随机量。

种群进行全局搜索或局部开发由切换概率P决定，P∈[0，1]，具体为:

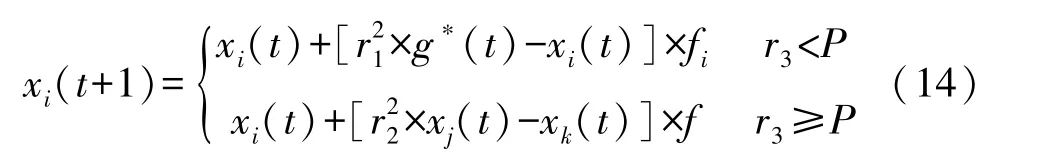
式中:r3∈[0，1]，为随机量。

3 动态分级蝴蝶优化算法DLBOA

3.1 基于混沌映射的种群初始化

研究表明，初始种群位置优劣直接影响着群智能优化算法的收敛速度和解的质量。 均匀的初始分布比随机分布对解空间的覆盖率更高，更容易生成质量更高的初始解。 标准BOA 算法采用随机方式生成初始种群的位置，具体方法是:

式中:Rand 为[0，1]间的随机生成量，xi为个体位置，[lbi，ubi]为个体i的搜索范围。 但这种方式并不能确保覆盖整个解空间。

混沌序列对比随机搜索，具有遍历性、随机性和规律性特征，可以更高的概率对解空间进行全局搜索，确保种群多样性。 根据以上分析，本文首先在改进算法中利用遍历均匀性和迭代速度更快的Tent混沌映射生成初始个体位置，尽可能覆盖整个解空间，具体公式为:

式中:yi(t＋1)为[0，1]间的混沌序列值。 根据混沌序列值可以逆映射到种群的初始位置，计算方式为:

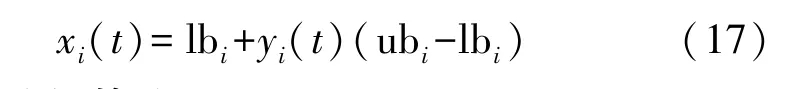
3.2 动态分级策略

对于基本BOA 算法而言，随着迭代更新，种群个体的适应度都有所不同。 邻近最优解的个体适应度更优，远离最优解的个体适应度则更差。 而为了同时兼顾种群的全局搜索和局部开发能力，种群也需要拥有这种多样性特征。 但所有个体如果采用相同的位置更新方式，势必会影响算法的寻优效率。为此，本文将引入一种动态分级方法，根据每次迭代中种群个体适应度值的升序排列，将种群动态地划分为差质种群个体、中等种群个体和优质种群个体。同时，对于不同的种群划分，利用不同策略对其个体进行位置更新。 算法结构如图2 所示。

图2 动态分级蝴蝶优化算法

令种群个体总数为n。 若令排序后的差质种群个体数量为p，中等种群个体数量为q-p，优势种群个体数量为n-q，则种群的动态分级模型可表示为:

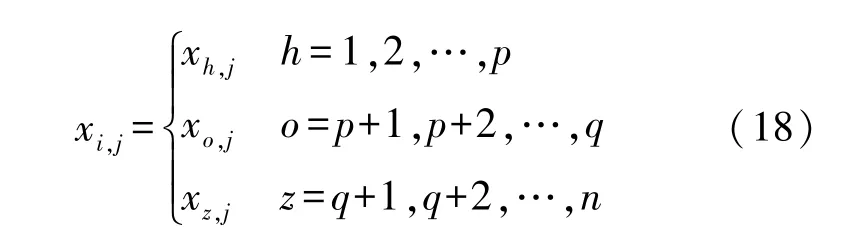
随着算法迭代，种群适应度会逐步提升，即优势种群规模会逐步扩大，此时应该控制不同分级种群的规模，扩大优势种群规模，使算法能够在精英引导机制下，实现算法的快速收敛。 具体地，将种群分级边界值动态地设置为:

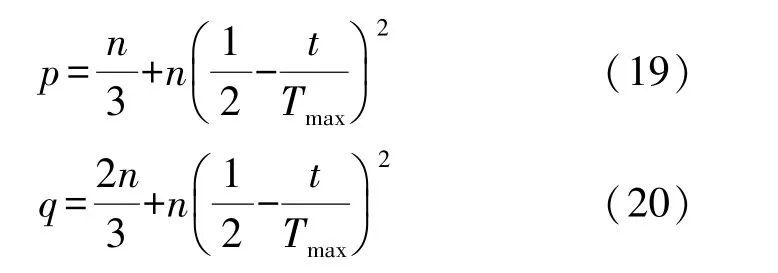
(1)针对差质种群的黄金正弦变异扰动机制

差质种群个体位置适应度较差，说明此时距离最优解区域较远，因此，为了避免局部最优，需要引入变异机制对差质个体进行扰动，以提高种群的多样性。 为此，本文引入一种基于黄金正弦算法(Golden-Sine Algorithm，GSA) 的变异扰动机制。GSA 算法是一种新型元启发式算法，受启发于正弦函数遍历单位圆所有正弦值等同于个体在搜索空间内的迭代寻优过程，通过构造正弦函数数学模型求解优化问题。 对于适应度较差的差质种群，引入黄金正弦的位置更新方式对个体进行更新，具体方式为:

式中:g*(t)为当前差质种群中的最优个体，R1∈[0，2π]，R2∈[0，π]，均为随机数，R1决定个体迭代时的移动距离，R2决定个体迭代时的移动方向，θ1、θ2是根据黄金分割数τ=(51/2-1)/2 得出的系数，且θ1=-π＋(1-τ)×2π，θ2=-π＋τ×2π，该系数缩小了算法的搜索空间，可引导个体向最优解逼近。

(2)针对中等种群的惯性权重位置更新机制

对于中等种群，其适应度处于中间部分，离最优解距离不是最远，但进化速度较慢。 为了加速算法收敛，中等种群位置更新在维持原始BOA 算法位置更新方式的基础上，引入粒子群算法PSO 中的惯性权重思维[15]，控制蝴蝶个体的社会学习与认知学习能力。 惯性权重的思想是:迭代早期，以较大惯性权重提升全局搜索能力；迭代晚期，以较小惯性权重增强局部开发能力，加速算法收敛。 此外，算法设计了一种自适应非线性惯性权重更新方法，具体公式为:

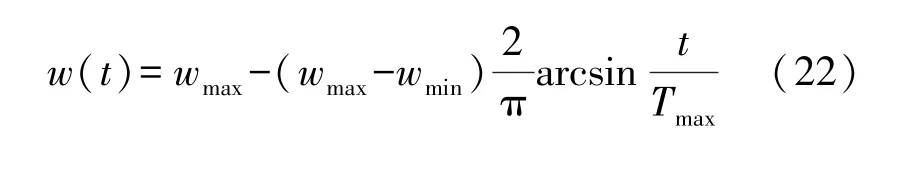
式中:wmax为初始惯性权重最大值，wmin为迭代结束时的惯性权重最小值。 则将中等种群的位置更新方式改进为:

(3)针对优势种群的精英引导机制

对于优质种群，由于已经接近于最优解，此时需要加快个体向最优解靠近。 为此，引入一种针对优质种群的精英引导策略，在位置更新中引入个体最优，通过精英引导加速算法收敛。 更新参数r1、r2后，利用控制参数cpi在精英引导方式和原种群更新方式之间切换，具体方式为:

式中:cp(t)为切换概率，设为cp(t)= 1/2-t/2Tmax，rand∈[0，1]，为随机数。 根据以上位置更新方式，迭代早期，cp(t)较大，个体倾向于用后两式更新位置，算法可以沿着最优解的方向加速进化；而迭代晚期，cp(t)较小，此时精英引导作用减弱，算法依然采用原始种群更新方式(前两式)更新种群位置。

DLBOA 算法的流程如图3。

图3 DLBOA 算法

4 DLBOA 算法求解WSN 节点覆盖

首先解决个体位置的编码映射问题。 传感器节点布署问题需要求解的是所布署的传感节点在区域内的横纵坐标值，可将DLBOA 算法中的蝴蝶个体位置编码为传感器节点的一个覆盖分布，蝴蝶位置的维度设置为传感器节点的两倍，即2V，并将维度2d-1 视为传感器节点d的横坐标，维度2d视为d的纵坐标。 如图4 是蝴蝶个体位置编码示意图，传感器节点Zi∈Z，i=1，2，…，V，Zi=(xi，yi)，xi∈[0，L]，yi∈[0，M]。

图4 个体位置编码

DLBOA 算法的优化目标是:将若干数量的传感器节点布署在监测区域S，在均衡能耗的要求下，以尽可能少的布署节点完成高区域覆盖率的目标，并求解相应节点布署的最优坐标位置。 此时，节点布署覆盖优化问题即适应度函数(8)为目标函数的高维复杂矢量寻优问题，节点布署位置的寻优过程可抽象为改进蝴蝶优化算法中蝴蝶的觅食寻优行为。

覆盖优化的具体求解步骤如下:

输入:布署区域大小S=L×M、传感器节点总数V、节点感知半径r、通信半径R；DLBOA 算法参数:种群规模n、迭代总次数Tmax、个体搜索区间[lb，ub](对应布署区域大小)、惯性权重初值wmax和终值wmin、切换概率P；

输出:传感节点布署的坐标位置及最优目标函数值；

步骤1 输入网络参数、DLBOA 算法参数；

步骤2 利用混沌映射进行种群初始化，生成初始传感节点布署位置坐标；

步骤3 令迭代t=1；

步骤4 计算种群适应度，确定全局最优解，并计算蝴蝶个体的香味浓度值；

步骤5 按适应度值对种群个体进行降序排列，按式(18)对种群动态分级，划分为差质种群、中等种群和优质种群；

步骤5a 对于差质种群个体，按式(21)进行位置更新；

步骤5b 对于中等种群个体，先以式(22)更新惯性权重，再以式(23)更新位置；

步骤5c 对于优质种群个体，以式(24)更新位置；

步骤6 重新计算种群适应度，并更新全局最优解；

步骤7t=t＋1；

步骤8 判断迭代条件t≤Tmax? 若满足，返回步骤4；否则，算法结束，输出传感节点布署的坐标位置及最优目标函数值。

5 实验分析

为了验证方法的有效性，利用两个实验场景进行性能分析。 实验场景1:令布署区域大小S=60 m×60 m，传感器节点总数V=80，传感器感知半径r=5 m，通信半径R=10 m。 实验场景2:令布署区域大小S=100 m×100 m，传感器节点总数V=100，传感器感知半径r=8 m，通信半径R=15 m。 传感器初始能量Estart=1 J，目标函数中的权重w1=0.6，w2=0.2，w3=0.2。 DLBOA 算法参数中，种群规模n=40，迭代总次数Tmax=400，惯性权重初值wmax=0.9，终值wmin= 0.4，切换概率P= 0.7。 实验环境为Windows10操作系统，CPU 主频为3.0 G，内存为8 GB，实验平台为MATLAB 2019b。 利用节点随机布署方法 RAND、 混沌优化细菌觅食算法COBFA[6]、自适应动态混沌量子粒子群算法DACQPSO[8]和本文的DLBOA 算法进行性能比较。

实验场景1 结果分析:图5～图8 是分别利用随机算法RAND、COBFA 算法、DACQPSO 算法和DLBOA算法得到传感器节点布署情况，区域内的黑色实心点代表传感器节点(位置坐标)，围绕节点周围的圆形为其覆盖区域。 由于前文覆盖模型中已将覆盖区域简化为L×M个像素点，则若总计有K个像素点被传感器节点覆盖，则其覆盖率为K/(L×M)。观察RAND 算法得到的节点布署结果，其覆盖盲区还是比较多，包括左下角、右侧边界、上边界以及中间位置区域均存在有覆盖盲区，同时在左侧上下区域和右上区域有明显的传感器节点密集分布，节点冗余度太高，这显然不能满足高覆盖率的传感器节点布署需求。 COBFA 算法和DACQPSO 算法得到的节点布署结果较明显地减少了覆盖盲区，节点分布的均匀性有所提升，但依然存在小面积的覆盖盲区。 在节点密度导致的冗余问题上，DACQPSO 算法略优于COBFA 算法，前者基本不存在较密集的节点分布，后者在中间区域的节点密度、重复覆盖位置略高，说明两种改进算法的位置精度还有提升空间。 而本文的DLBOA 算法可以在区域内得到更均匀的传感节点分布，基本没有覆盖盲区，节点间距更加平均，使得节点覆盖冗余更少，这说明算法在求解布署位置上具有更高的精度，更好地满足了目标函数的最优化。

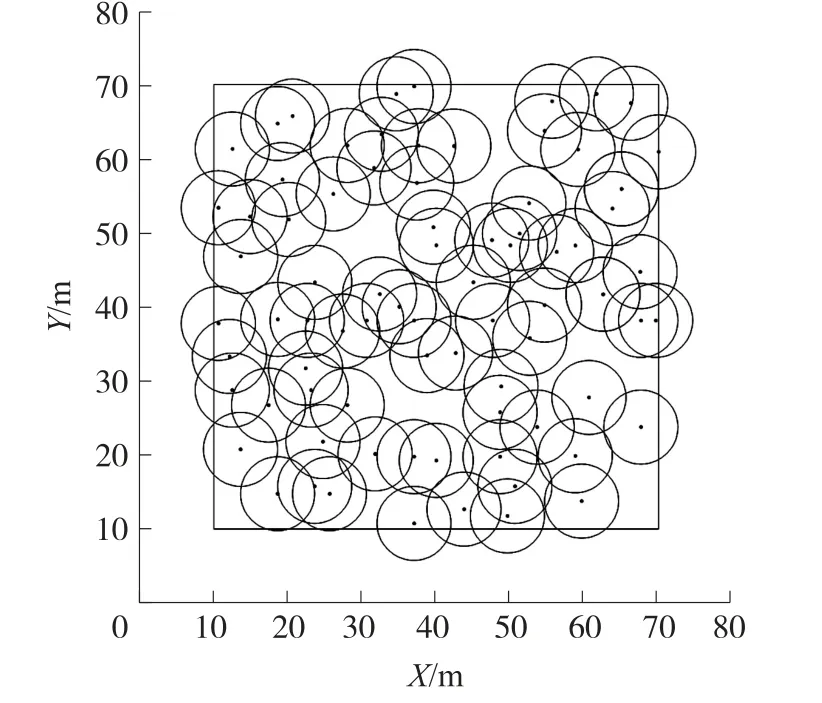
图5 实验场景1 RAND 算法节点随机布署

图7 实验场景1 DACQPSO 算法的节点覆盖图

图8 实验场景1 DLBOA 算法的节点覆盖图

图9 是网络覆盖率的收敛曲线。 从网络覆盖率上看，本文的DLBOA 算法在进行200 次迭代后，覆盖率已经接近100%，是四种算法中最好的。 其次是DACQPSO 算法和COBFA 算法。 曲线的斜率可以反映算法对前次迭代中传感器节点位置的修正情况，三种智能优化算法的曲线明显要更加陡峭，说明节点位置调整后对网络覆盖率有了较大提升。 而RAND 算法基本是平缓的直线走势，调整幅度有限，覆盖率也比较低。 DACQPSO 算法和COBFA 算法的网络覆盖率之所以无法进一步提升的原因在于，种群进化已经处于局部最优解处，算法无法跳离该位置，即无法进一步找到最佳的节点布署位置。 在网络覆盖率上，DLBOA 比DACQPSO、COBFA 和RAND 算法分别高出4.3%、11.5%和17.8%。 同时，DLBOA 算法可以以更少迭代次数得到更高的网络覆盖率，说明算法求解精度不仅更高，其演化速度也是更快的。

图9 实验场景1 覆盖率的变化

图10 是传感器节点布署数量对网络覆盖率的影响。 节点布署数量增加，势必会增加网络覆盖率，但算法表现各有不同。 RAND 算法的增长速度最为缓慢，节点布署位置并未得到优化。 DLBOA 算法增长速度最快，同时也是四种算法中覆盖率最高的。此外，若布署传感器节点较少，无论利用哪种算法，节点密集和交叉覆盖的情况会相对较少，所以算法之间在覆盖率上并没有较大差距。 但当传感节点数量增长到一定程度时，节点交叉区域变多，若不对布署位置精确求解，显然会出现覆盖空洞和节点密集等情况。 可以看到，DLBOA 算法在增加节点数量后的覆盖率增长明显更快，最后接近于全覆盖，这更加佐证了改进蝴蝶优化算法在求解精度上得到了进一步提高，可以较少的节点布署数量维持较高的网络覆盖率。

图10 实验场景1 传感器节点布署数量对覆盖率的影响

实验场景2 结果分析:场景2 的布署区域和节点覆盖半径都有相应增加，四种算法的节点分布情况如图11～图14 所示。 RAND 算法的覆盖盲区依然很多，部分区域的传感器节点分布也过于密集，冗余度过高。 COBFA 算法和DACQPSO 算法的节点布署明显减少了覆盖盲区，分布均匀性更好，但依然存在个别位置的空白。 此外，DACQPSO 算法在节点密集冗余分布上要优于COBFA 算法，COBFA 算法还是存在较严重的重复覆盖问题，说明算法的寻优性能、位置布署精度有待改善。 DLBOA 算法得到的节点具有更均匀的分布，覆盖冗余更少，更加有效地利用了传感节点的单点覆盖面积，节点间距也更加平均。

图11 实验场景2 RAND 算法节点随机布署

图12 实验场景2 COBFA 算法的节点覆盖图

图13 实验场景2 DACQPSO 算法的节点覆盖图

图14 实验场景2 DLBOA 算法的节点覆盖图

结合图15 给出的网络覆盖率收敛曲线可知，扩大布署区域后，DLBOA 算法迭代250 次左右后，覆盖率已接近100%，收敛速度要优于另外三种算法。两种智能算法处于收敛处的网络覆盖率无法接近于100%的原因在于，其算法求解的是局部最优解，算法无法有效跳离局部极值点而开拓新的搜索空间得到候选解。 在平均网络覆盖率上，DLBOA 算法比DACQPSO、COBFA 和RAND 算法分别高出8.2%、16.5%和22.6%。

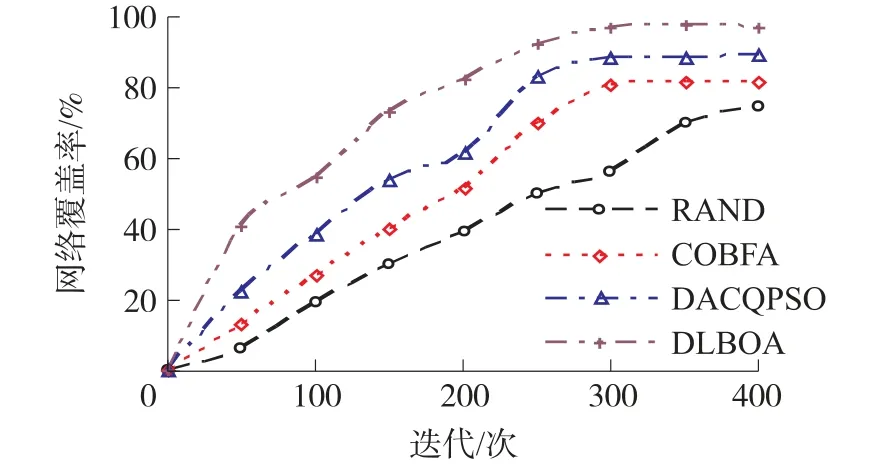
图15 实验场景2 覆盖率的变化

图16 是该场景下传感器节点布署数量对网络覆盖率的影响。 可见，DLBOA 算法在增加节点数量后的覆盖率增长依然是所有算法中更快的，最后的网络覆盖率也接近于全覆盖。 经过两个不同规模布署场景的验证，证明DLBOA 算法具备稳定的性能表现。

图16 实验场景2 传感器节点布署数量对覆盖率的影响

无线传感器网络的最终目标是通过传感节点的数据收集和自组网络将信息传输到远端的汇聚基站。 由于传感节点多由电池供电，能耗有限，节点布署位置直接影响数据传输距离。 结合节点的能耗模型，本部分进一步观察不同布署算法下网络的生存时间，且该生存时间直接由区域内存活的传感器节点数量决定。 选取经典的分簇路由协议LEACH 对传感器节点自组织成网，图17 是在实验场景1 下四种算法进行节点布署后，协议运行100 轮次过程中，网络节点存活量的变化情况。 根据实验结果，出现第一个死亡节点的轮次顺序是RAND 早于COBFA，COBFA 早于DACQPSO，DLBOA 算法最晚，由于传感节点主要能耗集中于数据传输能耗，因此该结果的原因可解释为:若节点布署不均匀，部分区域节点密度高，冗余节点多，数据重复传输过多，节点能耗更快；而未覆盖的空洞区域则需要更多次的远距离数据中继，同样会使节点能耗加快。 DLBOA 算法以更少的传感节点布署量覆盖更多区域，数据传输距离均等，避免了过多的远距离传输和近距离冗余传输，在有限的能量储备下延长了节点的工作时间，从而也延长了整个网络的工作时间。 表1 是各算法间的系统比较结果，可以看到，在平均网络覆盖率、布署节点数量以及剩余网络能量三个方面，DLBOA 算法均要优于另外三种算法。

表1 算法系统比较

图17 传感器网络的生存时间

影响DLBOA 算法性能的主要参数为惯性权重初值wmax和终值wmin以及切换概率P。 在前文场景1、场景2 中设置的参数wmax=0.9、wmin=0.4 和切换概率P=0.7 是根据文献阅读所取的经验值，也是多数算法中取值的最优组合。 为了算法的严谨性，本部分根据不同的取值组合验证算法的寻优性能。 惯性权重w和切换概率P均对DLBOA 算法在迭代前后期的全局搜索与局部开发能力的切换具有重要影响。 分别选取四组参数组合进行实验测试，惯性权重的四组取值组合为(wmin，wmax)=(0.2，0.7)、(0.3，0.8)、(0.4，0.9)和(0.5，0.8)，切换概率P=0.5、0.7、0.8 和0.9。

固定P=0.7，改变惯性权重取值进行第一组实验，利用场景1 配置实验环境，结果如图18 所示，柱状图对应左纵坐标取值，折线图对应右纵坐标取值。结合网络平均覆盖率和网络剩余能量指标看，惯性权重取值对DLBOA 算法的寻优结果具有一定影响。 (0.4，0.9)的取值组合下算法可以得到最优的覆盖率，虽然优势并不明显，但依然是四种取值中最佳的。 固定(wmin，wmax)= (0.4，0.9)，改变切换概率取值进行第二组实验，结果如图19。 概率阈值P直接决定了DLBOA 算法在全局搜索与局部开发间的切换。P取值越大，越易进入全局搜索阶段；反之，越易进入局部开发阶段。 结果显示，P=0.7 和0.8时，平均覆盖率较接近，几乎相等。 而网络剩余能量指标上，P=0.7 时略优于0.8。 对于蝴蝶种群进化过程而言，若P值较大，全局搜索比重则更大，会导致算法收敛慢；若P值过小，局部开发比重则增加，会导致算法种群多样性缺失，搜索精度下降。 合理的搜索应在迭代前期具有更强大的全局搜索能力，迭代后期则应加强局部开发能力，加快寻优收敛。 切换概率的常量设定也具有一定局限性，动态调整全局搜索与局部开发比重，以自适应方式设置切换概率将是下一步优化的目标。

图18 惯性权重取值的影响

图19 切换概率取值的影响

6 结束语

提出一种基于动态分级蝴蝶优化算法的节点布署策略。 为了提高传统蝴蝶优化算法的寻优精度和速度，引入混沌映射进行种群初始化，确保种群多样性；采用动态分级策略，根据种群个体适应度，将蝴蝶种群划分为差质、中等和优质三种等级，并分别利用黄金正弦算法、惯性权重位置更新和精英引导机制对三类种群进行优化，提高算法的收敛速度，增强脱离局部最优的能力。 将动态分级蝴蝶优化算法应用于求解传感器节点的覆盖优化问题，以融合区域覆盖率、能量均衡和节点闲置率的目标函数作为算法的适应度函数，对传感器节点的布署位置进行迭代寻优。 结果表明，改进算法能够有效优化传感节点布署，提高网络覆盖率，延迟节点死亡。 如何构建更加复杂的布署模型，如存在非均匀遮挡或衰减分布的实验场景，将是下一步需要深入研究的问题。