多策略混合的改进麻雀搜索算法

回立川，陈雪莲，孟嗣博

辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105

群智能优化算法的主要思想是从自然界的生物系统中寻求解决问题的灵感和方法[1]。目前主要的群智能算法有粒子群算法（particle swarm optimization，PSO）[2]、人工萤火虫群优化算法（glowworm swarm optimization，GSO）[3]、遗传算法（genetic algorithm，GA）[4]、灰狼优化算法（grey wolf optimizer，GWO）[5]、磷虾群算法（krill herd algorithm，KH）[6]等，这些典型的群智能优化算法已经被应用于解决许多经典优化算法难以解决的大规模优化问题。

薛建凯等[7]于2020年提出一种新型的群智能算法，即麻雀搜索算法（sparrow search algorithm，SSA）。与其他群智能算法相比，SSA 具有较高求解精度和效率，同时拥有鲁棒性强、稳定性好等优点。但在种群迭代后期，同其他群智能算法类似，出现收敛速度慢、易陷入局部最优等缺点[8]。

针对这些缺陷，吴丁杰等[9]将Logistic混沌映射和线性递减权重法引入SSA，使初始解的质量得到改善，降低了算法易早熟的风险。吕鑫等[10]将Tent 混沌高斯变异引入SSA，提高了寻优精度，具有优良的开拓能力且表现出良好的实时性和稳定性。毛清华等[11]将Sin混沌映射、动态自适应权重、柯西变异以及反向学习策略应用到SSA，有效提高了全局探索性能。张伟康等[12]将Circle 混沌映射、蝴蝶优化策略和逐维变异策略引入麻雀搜索算法，增加了搜索空间和种群多样性，提高了全局探索性能。李爱莲等[13]将折射反向学习、正余弦算法以及柯西变异引入麻雀搜索算法，解决了种群多样性不足造成的麻雀在迭代后期出现停滞问题，从而扩大了麻雀觅食范围。唐延强等[14]将猫映射混沌序列、柯西变异和Tent混沌扰动引入SSA，有效使陷入局部极值点的个体跳出限制。虽然以上学者对基本SSA 的改进在一定程度上丰富了种群多样性，提升了全局寻优能力，但仍存在算法求解精度不足、开发能力弱等缺陷。

本文提出一种多策略混合的改进麻雀搜索算法（improved sparrow search algorithm based on multistrategy mixing，IMSSA）。首先利用Sine混沌映射初始化麻雀个体位置，丰富种群多样性，解决种群分布不均匀、搜索空间不足等问题；然后引入带有惯性权重的多样性全局最优引导策略引领麻雀向最优位置迁徙，提升收敛速度，平衡算法的全局堪探与局部开拓能力；最后对跟随者使用双样本学习策略，使其跳出局部最优，提升麻雀种群的寻优性能。通过12个经典测试函数将6个算法和2个最新改进的SSA与本文所提算法进行对比，并对改进策略进行有效性验证，充分体现了IMSSA 在函数优化问题上的可行性和优越性。最后，选用5个性能优越的算法对支持向量机参数进行优化并建立轴承故障诊断模型，对比各模型的分类准确度，证明了IMSSA具有一定的应用价值。

1 基本麻雀搜索算法

SSA主要模仿麻雀群的觅食过程，麻雀群觅食过程也是一种探索者-跟随者模型，同时还叠加了侦查预警机制。探索者一般具有较好的适应度值，携带更多的优势信息，其附近往往能找到更好的觅食位置，搜索范围广。探索者一般占到种群的10%～20%。跟随者会跟随具有最佳适应度值的探索者来搜索和寻找食物，并且为了提高自己的捕食率可能会不断监视探索者，争夺食物源。当麻雀意识到危险时，会即刻表现出反捕食状态。

假设在D维解空间内存在N只麻雀，则每只麻雀的位置为X=[x1,x2,…,xN]T,适应度值为Fx=[f(x1),f(x2),…,f(xN)]T。

在SSA中，适应度值较好的探索者在觅食过程中可以优先获得食物，并为所有跟随者提供搜索方向。探索者的位置更新公式如下：

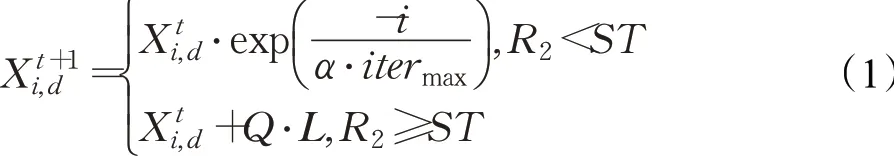
式中，t为当前迭代次数；itermax为最大迭代次数；Xi,d为第i只麻雀在第d维位置；Q为服从正态分布的随机数；随机数α∈( ]0,1 ；L为1×d的矩阵，且矩阵内每个元素为1；R2∈[0,1] 表示预警值；ST∈[0.5,1] 表示安全值。当R2＜ST时，表示觅食环境无害，探索者可以进行广泛搜索。

当R2≥ST时，表示警戒者已发现捕食者，并发出警报，此时所有麻雀都需要向安全区靠拢。

跟随者的位置更新公式如下：

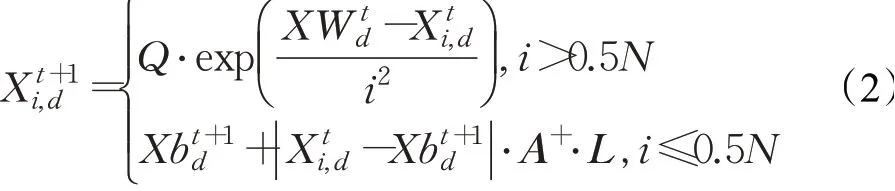
式中，XW表示当前种群中麻雀最差位置；Xb表示当前种群中麻雀最优位置；A为1×d的矩阵且元素随机赋值为1或-1，A+=AT(AAT)-1。

当i ＞0.5N时，表示适应度较差的第i个跟随者没有取得食物，能量极低，处于十分饥饿状态，需立即飞往其他区域觅食；当i≤0.5N时，表示第i个跟随者将在当前最优位置Xb附近寻找食物。

为了觅食过程的安全性，每代种群中会随机挑选10%～20%的麻雀负责警戒。警戒者位置更新公式如下：

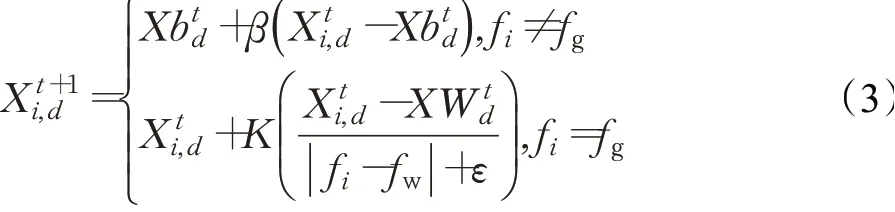
式中，ε为常数；β为步长控制参数；K∈[-1,1] 表示移动方向的随机数；fi为当前麻雀个体适应度值；fg为当前全局最佳适应度值；fw为当前全局最差适应度值。

当fi≠fg时，表示麻雀在种群边缘，极易被捕食者袭击；当fi=fg时，表示麻雀在种群中间，并且已经觉察到危险，为躲避袭击需及时向其他麻雀靠近。

2 麻雀搜索算法的改进

2.1 Sine混沌映射优化初始种群

SSA在搜索空间内随机建立初始种群，可能导致麻雀种群分布不均匀、搜索空间不足等问题。而混沌具有遍历性和随机性，可以很好解决这些问题[15]。

本文采用Sine混沌映射来初始化种群，Sine混沌映射定义如下：

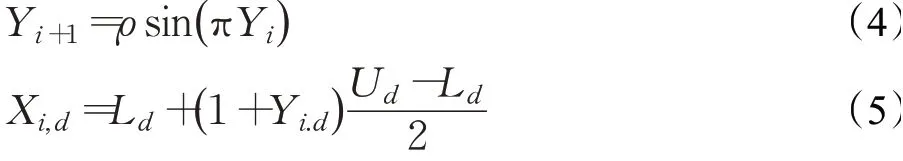
式中，Yi∈[ ]-1,1 为混沌序列；ρ为控制参数；Ud、Ld分别为麻雀个体在第d维的上下限。

Sine 映射具有较好的混沌特性，其混沌性与参数ρ的取值有着很大的关系。由图1 所示，ρ∈[ ]0.87,1 且ρ越接近1，混沌性能越好，Yi越均匀地分布在[ ]-1,1 区域内。当ρ=1 时，系统处于完全混沌状态，因此之后的实验都取ρ=1。根据式（5）将式（4）产生的变量值映射到麻雀个体上，可得到种群的初始解位置。

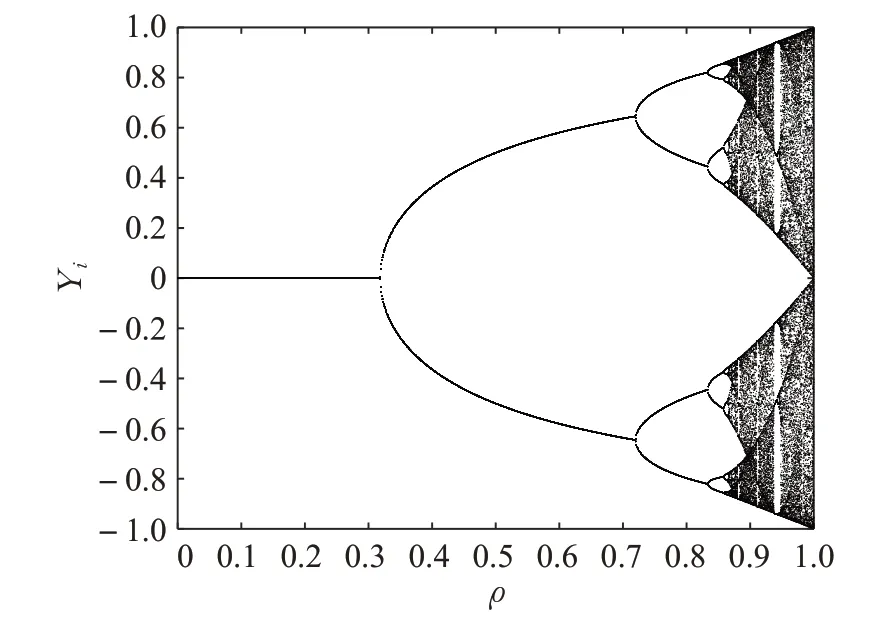
图1 Sine混沌序列分岔图Fig.1 Bifurcation diagram of Sine chaotic sequence

如图2 所示，搜索空间内种群分布的均匀性较好，因此将Sine混沌映射应用到SSA算法，可使初始解分布更均匀，扩大搜索范围，既能防止在搜索过程中陷入局部极小值，又可确保种群多样性，从而提高算法的寻优效率，改进基本麻雀算法的不足。

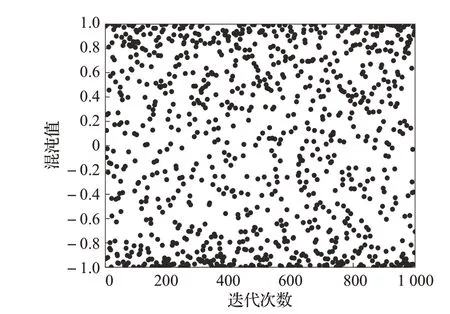
图2 Sine混沌序列分布图Fig.2 Distribution diagram of Sine chaotic sequence

2.2 带有惯性权重的多样性全局最优引导策略

2.2.1 多样性全局最优引导

探索是指在搜索空间中寻找未知领域，探索能力愈强，则全局寻优结果愈好，但会减缓收敛速度。开发是指利用前期所得的较好解去搜寻更优解的能力。开发能力愈强，则局部寻优效果愈好，收敛速度愈快，但易造成早熟现象，只有平衡好这两种能力才会使算法性能更优[16]。

标准的SSA算法中的发现者在寻找最优位置时，容易偏离方向，错过最优的觅食区域，导致算法陷入局部最优。鸽群优化算法[17]中鸽子利用磁接收在大脑中塑造地图来感知地球磁场，把太阳的高度当作指南针来调整方向，使算法收敛得更快、更稳定，改善了算法的局部开发和全局探索能力，具有鲁棒性较强等优点，并且使生成的最优路径更平滑、更令人满意。因此将鸽群优化算法中地图罗盘算子引入麻雀搜索算法中的探索者位置更新过程。

在探索者位置更新过程中增加全局引导项来提高算法的全局空间探测能力。种群中的麻雀个体主要由处于全局最优位置的麻雀引导，它引导整个种群去寻找最优食物源，因此种群中的麻雀个体可以在不受任何干扰的情况下移动到全局最优位置，加快了收敛至当前全局最优位置的速度[18]。

改进后的探索者的位置更新公式为：

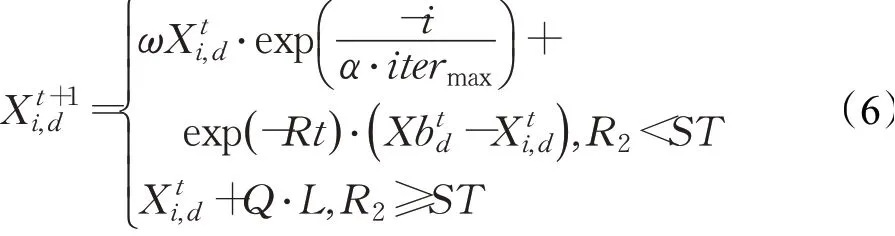
式中，R为地图罗盘算子，介于0到1之间；ω为惯性权重；t为当前迭代次数；Xbd是地图罗盘在第d维指示的位置，即当前全局最优位置，它引导着所有麻雀向着最优解靠拢，使算法全局探索能力增强。

2.2.2 自适应惯性权重

惯性权重对麻雀搜索算法性能影响巨大，在[0，1]范围内，惯性权重愈大，则全局探索能力愈强，种群的多样性愈丰富；惯性权重愈小，则算法的局部开采能力愈强，收敛速度愈快[19]。因此本文提出了一种非线性惯性权重公式如下：

当α=0.7,β=0.3 时，ω的值在[0，1]之间随着迭代次数的增加呈现非线性递减趋势。如图3所示，迭代前期，ω的衰减速度随着迭代次数的增加由快变慢，有利于全局搜索，以较快的速度向全局最优或较优的位置靠拢；迭代中后期，惯性权重的衰减速度缓慢下降，利于更精细地进行局部开采，提升算法的整体寻优能力，并且在一定程度上加快收敛速度，提高最优解的质量。随着惯性权重不断变化，全局探索阶段的麻雀个体可以更好寻得全局最优解或较优解的大概位置，因而该算法可以在局部精细搜索过程中更快、更容易地找到最优值。因此，加入非线性惯性权重有效增强了种群多样性，提高了算法的求解精度，平衡了算法在全局探索和局部开发时期的能力。

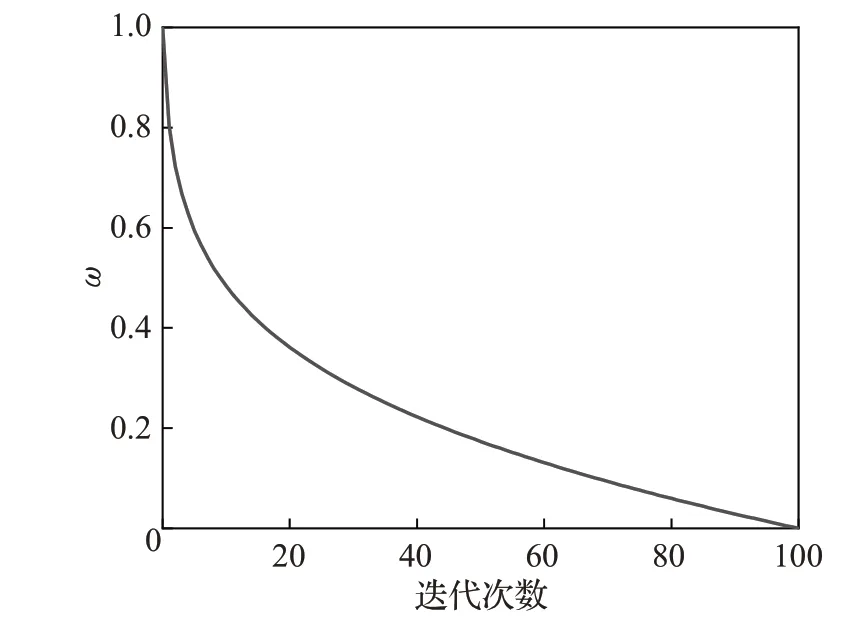
图3 惯性权重迭代过程Fig.3 Iterative process of inertia weight

2.3 双样本学习策略

在基本麻雀搜索算法中，麻雀的学习是盲目的，跟随者每次只选择一个比自身觅食位置好的探索者样本进行学习，但无法判断此次学习是否有利于找到最好的觅食区域，这种盲目的学习方法有益于算法对优化空间的探索，但也会使得种群的一部分重要位置信息丢失，导致算法开发能力弱、收敛速度慢以及易陷入局部最优。

为了解决这些问题，本文引入双样本学习[20]策略，改进SSA中跟随者的位置更新公式。如图4所示，解空间中有两个局部最优位置和一个全局最优位置，麻雀m和n已经陷入局部最优所处的区域，那么麻雀i无论是向m学习还是向n学习都会陷入局部最优解。

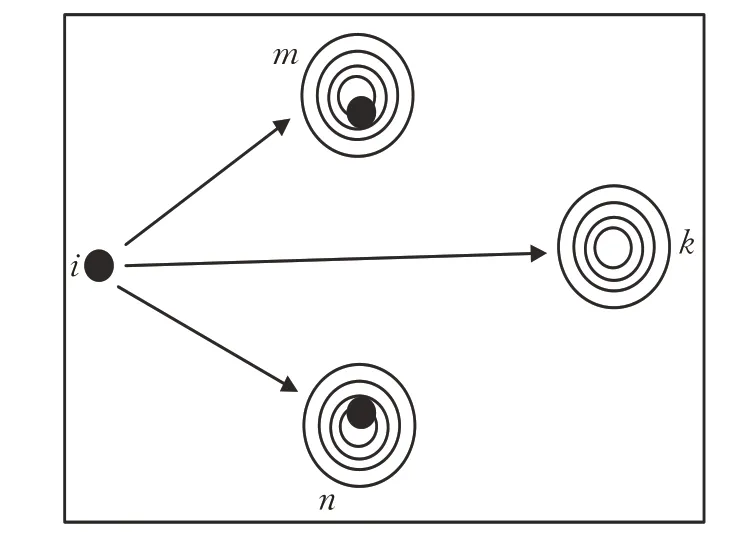
图4 双样本学习图Fig.4 Graph of double-sample learning

为了让i能探索到全局最优所处的区域k，令i同时向m和n学习，跟随者以两个探索者的混合信息为指引，这样便有更大的概率探索到当前优化空间未搜索到的食物源区域，使算法跳出局部最优，进一步提高种群对优化空间的堪探能力。改进后的跟随者位置更新公式如下所示：

2.4 改进算法的流程描述

基于前文所述的改进策略，本文改进麻雀搜索算法的具体流程如图5所示。

图5 改进麻雀搜索算法的流程图Fig.5 Flow chart of improved sparrow search algorithm

本文所提的多策略混合的改进麻雀搜索算法步骤如下：

步骤1 设置种群规模N，探索者比例PD，警戒者比例SD，定义迭代次数T，空间维度D，并根据式（4）和式（5）初始化种群位置。

步骤2 计算麻雀适应度值和平均适应度值并进行排序。

步骤3 以所有麻雀的平均适应度值作为界限，适应度值大于平均适应度值的麻雀划分为探索者，依据式（6）和（7）更新探索者位置。

步骤4 适应度值不大于平均适应度值的麻雀划分为跟随者，依据式（8）更新跟随者位置。

步骤5 根据式（3）更新警戒者的位置。

步骤6 更新整个种群所经历的最优位置Xb和其适应度值fg，以及最差位置XW和其适应度值fw。

步骤7 是否符合停止条件，符合则退出，输出结果，否则继续执行步骤2～步骤7。

3 算法的性能测试

3.1 仿真实验环境

为了实验结果的公平性，所有测试均在同一环境下进行。实验环境为Windows10，64 位操作系统，处理器为AMD Ryzen 5 4600U with Radeon Graphics 2.10 GHz，RAM为16.0 GB，编程软件为MATLAB R2018b。

3.2 比较对象和参数设置

为了验证算法的优越性和可行性，本文采用SSA、GA、GSO、文献[21]改进的粒子群算法SCDLPSO（particle swarm optimization with self-correcting and dimension by dimension learning capabilities）、文献[22]改进的灰狼优化算法COGWO（grey wolf optimization based on cubic mapping and opposition-based learning）和文献[23]改进的磷虾群算法NLKH（krill herd with nearest neighbor lasso operator）共六种算法，在选取的12 个测试函数[24]下与本文所提出的IMSSA进行综合性对比。测试函数具体信息如表1所示。本文定义的种群规模N=200，迭代次数T=100，空间维度D=30，其余各参数设置如表2所示。

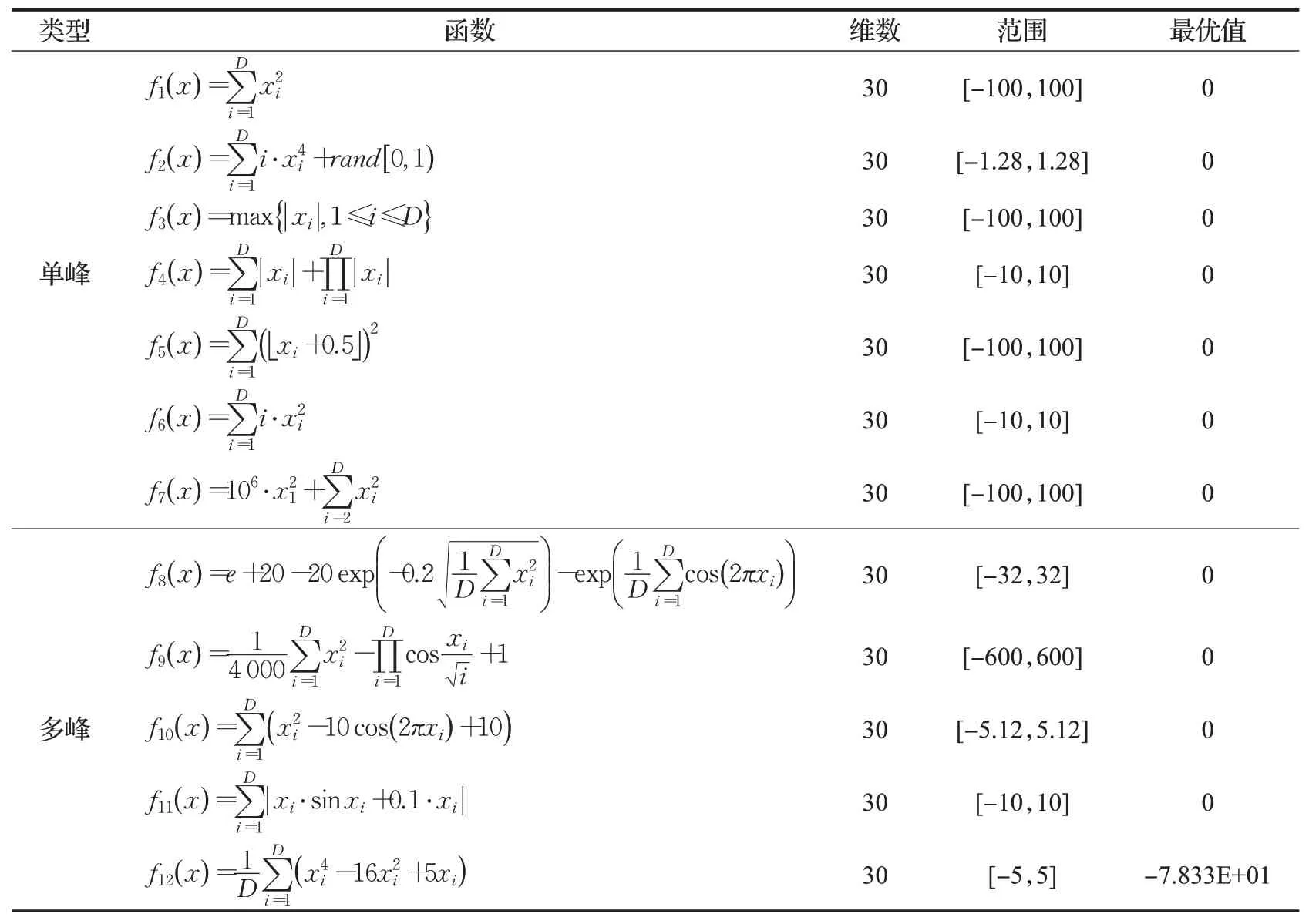
表1 测试函数Table 1 Test functions

表2 各算法参数设置Table 2 Parameter setting of each algorithm

3.3 算法性能对比分析

为验证IMSSA 寻优结果的准确性和稳定性，选取各测试函数独立运行50次的实验结果作为依据。针对12个测试函数，将各算法的最优值、最差值、平均值等作为最终评价指标，如表3所示。

由表3 中IMSSA 与其他六种算法的实验结果比较可以看出，IMSSA 虽在f2、f8下未达到理论最优值，但相比于SSA、SCDLPSO、GA、GSO、COGWO、NLKH 的求解精度仍有明显提高，并且非常接近理论最优解。IMSSA在其余10个测试函数下均取得理论最优值0，体现出了IMSSA 极强的寻优能力，说明本文采用的改进策略是可行有效的。在运行时间方面，IMSSA 运行时间最短，说明改进策略的引进没有提升SSA算法的时间复杂度，反而降低了执行时间。从各项指标均可看出，IMSSA 的值更小，表明了IMSSA 的鲁棒性和求解精度明显优于其余六种算法。

表3 （续）

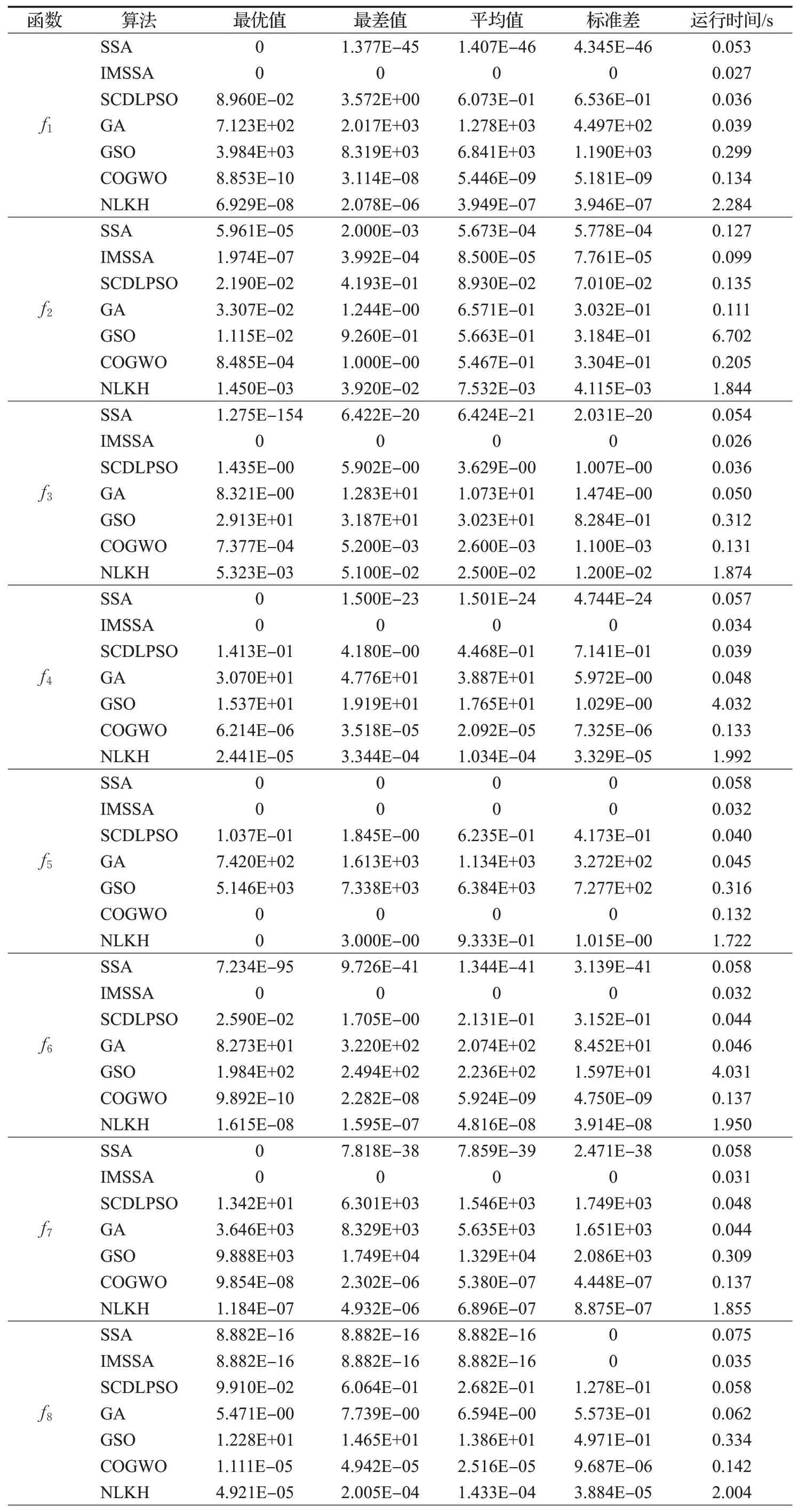
表3 测试函数结果比较Table 3 Comparison of test function results

3.4 算法收敛曲线对比分析

为了更直观地显示算法的收敛速度和寻优精度，并展示算法跳出局部空间的能力，本文依据迭代次数和适应度值得出了12 个测试函数的收敛曲线图。如图6 所示，IMSSA 在前期收敛速度相较于其他算法有着很大的提升，局部开发能力远高于其他算法，能够迅速地进行搜索空间的寻优遍历，从而大大缩短算法前期的探索周期，同时算法兼顾寻优精度，可以更加接近理想最优解。因为纵坐标是对数，而最小值0 没有对数，所以迭代后期没有出现相应的曲线。对于单峰函数f1、f3～f7，对比其他算法可以看出IMSSA的收敛速度最快且收敛精度最高，稳定性最强。对于单峰函数f2，虽然没有找到理论最优解，但IMSSA 的各项性能明显最优。对于多峰函数f9～f11,仍可以看出IMSSA具有较强的寻优能力，且抗停滞能力非常强，随着迭代次数的增加，其他算法逐渐趋于平缓，表明陷入不同程度的局部最优，且收敛精度较低，而IMSSA和SSA曲线仍呈下降趋势，尤其是IMSSA 下降速度最快，稳定性最好。对于多峰函数f8和f12，虽然IMSSA 与SSA 的收敛精度相同，但可以看出IMSSA的收敛速度明显优于SSA且不易陷入局部最优范围。综上所述，本文提出的IMSSA 不论是在单峰还是多峰测试函数上，都有较强的寻优性能和抗停滞能力，整体性能优于SSA和其他对比算法。

图6 测试函数收敛曲线图Fig.6 Convergence curves of test functions

3.5 与其他改进麻雀搜索算法比较分析

为了进一步体现本文提出的IMSSA 的优越性，选取了两个具有代表性的测试函数与吕鑫等[10]提出的混沌麻雀搜索算法（chaos sparrow search algorithm，CSSA）和张伟康等[12]提出的混合策略改进的麻雀搜索算法（mixed strategy to improved sparrow search algorithm，MSSSA）在同一条件下（以文献[12]中的条件为基准）得出的平均值与标准差进行了比较，实验结果如表4所示。

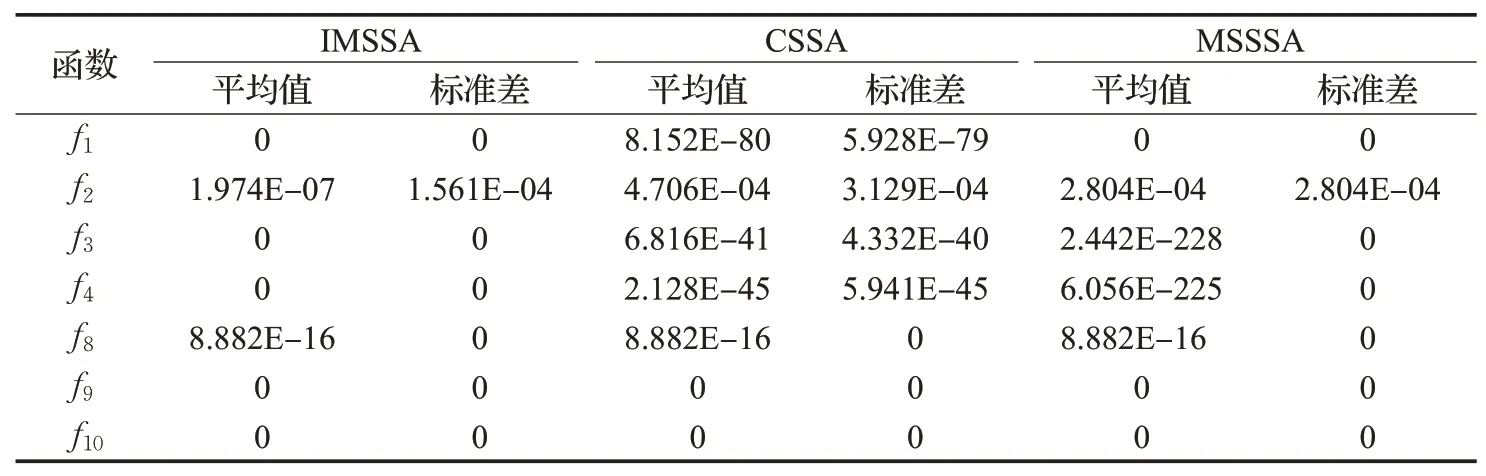
表4 IMSSA与CSSA、MSSSA算法性能比较Table 4 Performance comparison of IMSSA，CSSA and MSSSA algorithms

由表4 可知，对于单峰测试函数，IMSSA 的寻优性能和稳定性明显高于CSSA和MSSSA；相对于多峰测试函数，IMSSA 的优化效果与CSSA 和MSSSA 相当。总体而言，IMSSA 无论是在搜索精度还是稳定性方面均优于其他两种改进的麻雀搜索算法。

3.6 改进策略的有效性分析

因为IMSSA是在SSA的基础上使用三种策略改进才使其寻优能力变好，但是否会有策略不起作用还尚不知晓，所以需要进行验证。为比较不同改进策略对算法性能的影响，将SSA、IMSSA、仅采用Sine混沌映射改进的SSA算法（SSA-1）、仅采用带有惯性权重的多样性全局引导策略改进的SSA 算法（SSA-2）和仅采用双样本学习策略改进的SSA算法（SSA-3）在6个基准测试函数上做对比实验，实验结果如表5所示。

由表5可知，SSA-1、SSA-2、SSA-3和IMSSA在f6、f9～f11这4 个函数中的4 个评价指标均为0，说明4 个算法寻到理论最优值不是偶然性，而是算法的寻优能力强，稳定性好，说明本文采用的改进策略均提升了算法跳出局部最优的能力；在函数f2上，SSA-1、SSA-2、SSA-3 和IMSSA 虽然没有寻到最优，但与基本SSA 算法相比，寻优精度得到明显改善，且寻优能力和算法的稳定性都比SSA 强。IMSSA 比仅用单一策略改进的SSA算法在4个评价指标的求解上效果更好，说明在不同策略的共同影响下，算法的寻优能力和算法的稳定性得到最大程度的提升。在函数f8上，五种算法均未寻得最优解，但寻优性能相当。在运行时间方面，五种算法中IMSSA所耗时长相对较短。但会出现单一策略改进的SSA 耗时更短，由于在IMSSA 中加入改进策略之后，算法搜索区域更广，找到的解更多，导致算法的寻优时间变长，但均在合理范围之内。

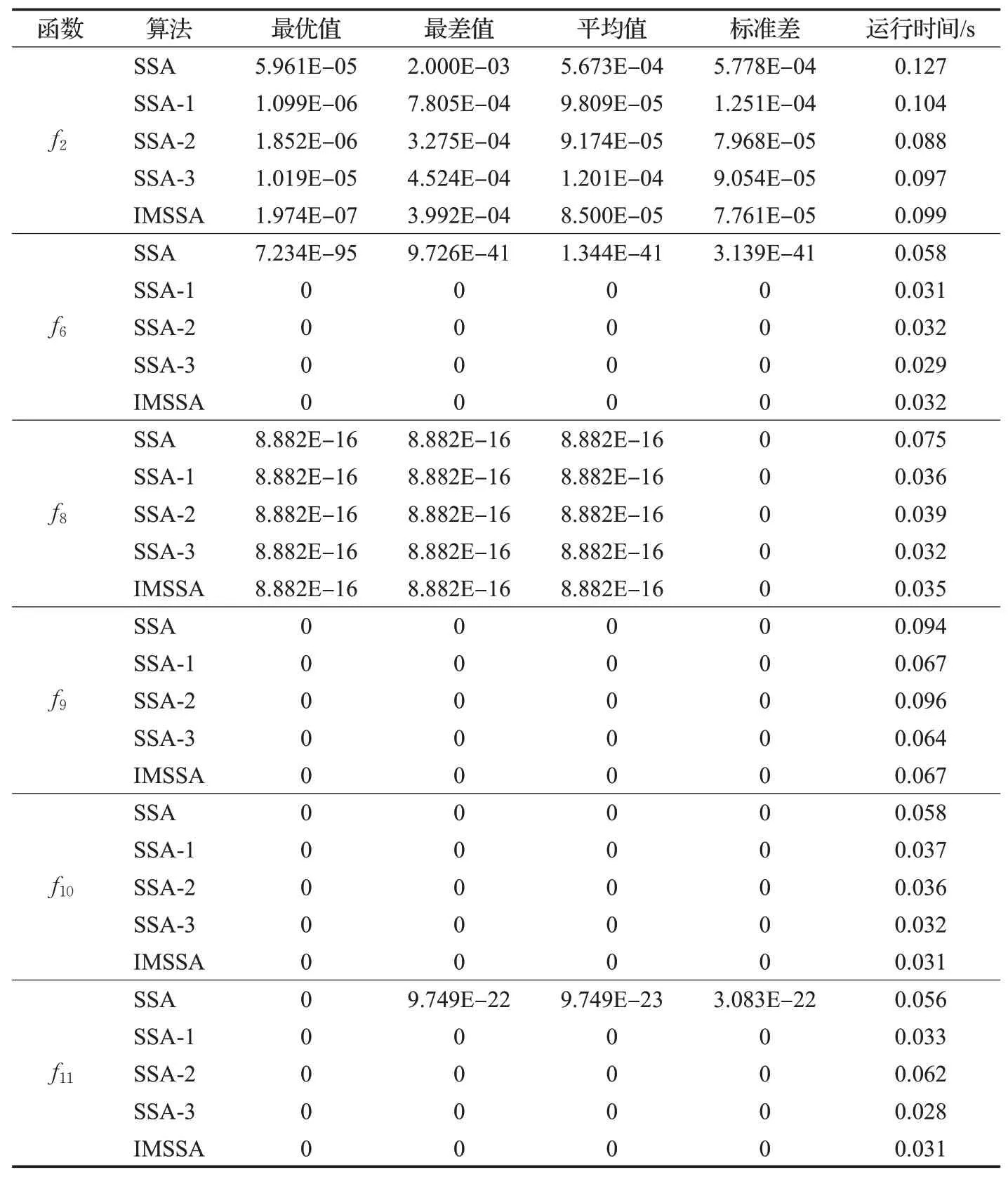
表5 不同改进策略实验测试结果Table 5 Experimental results of different improvement strategies

部分测试函数中每个策略都具有较强的寻优能力，无法清楚地反映出每个策略发挥的作用，因此需要由图7进一步地解释分析。

如图7所示，SSA-1、SSA-2、SSA-3比基本SSA算法的收敛速度快，而SSA-1、SSA-2、SSA-3 三者结合使IMSSA算法的整体收敛速度得到了有效的提升。在f2和f8测试函数中，IMSSA虽未达到理论最优值，但相较于其他四种对比算法，IMSSA 的寻优精度和收敛速度明显更优。在f6、f9～f11这4个测试函数中，五种算法的寻优能力都很强，但还是可以看出在迭代次数一样的条件下，IMSSA具有更高的收敛精度，在收敛精度一样的条件下，IMSSA具有更快的收敛速度。在6个测试函数中，三种单一策略改进的SSA在收敛速度和寻优精度方面较基本SSA 有略微提升，但是次于混合策略改进的IMSSA，说明每个策略都充分发挥了自己最大的作用，并且每个策略都是有效的。SSA-1 算法引入Sine 混沌映射保证了种群多样性，使搜索空间分布均匀；SSA-2算法引入带有惯性权重的多样性全局最优引导策略后，麻雀种群在最优个体和地图罗盘算子的引导下能够迅速聚集到最优食物源处；SSA-3算法引入双样本学习策略后，使算法跳出局部最优能力增强，进一步验证了本文采用三种策略混合改进算法的可行性。

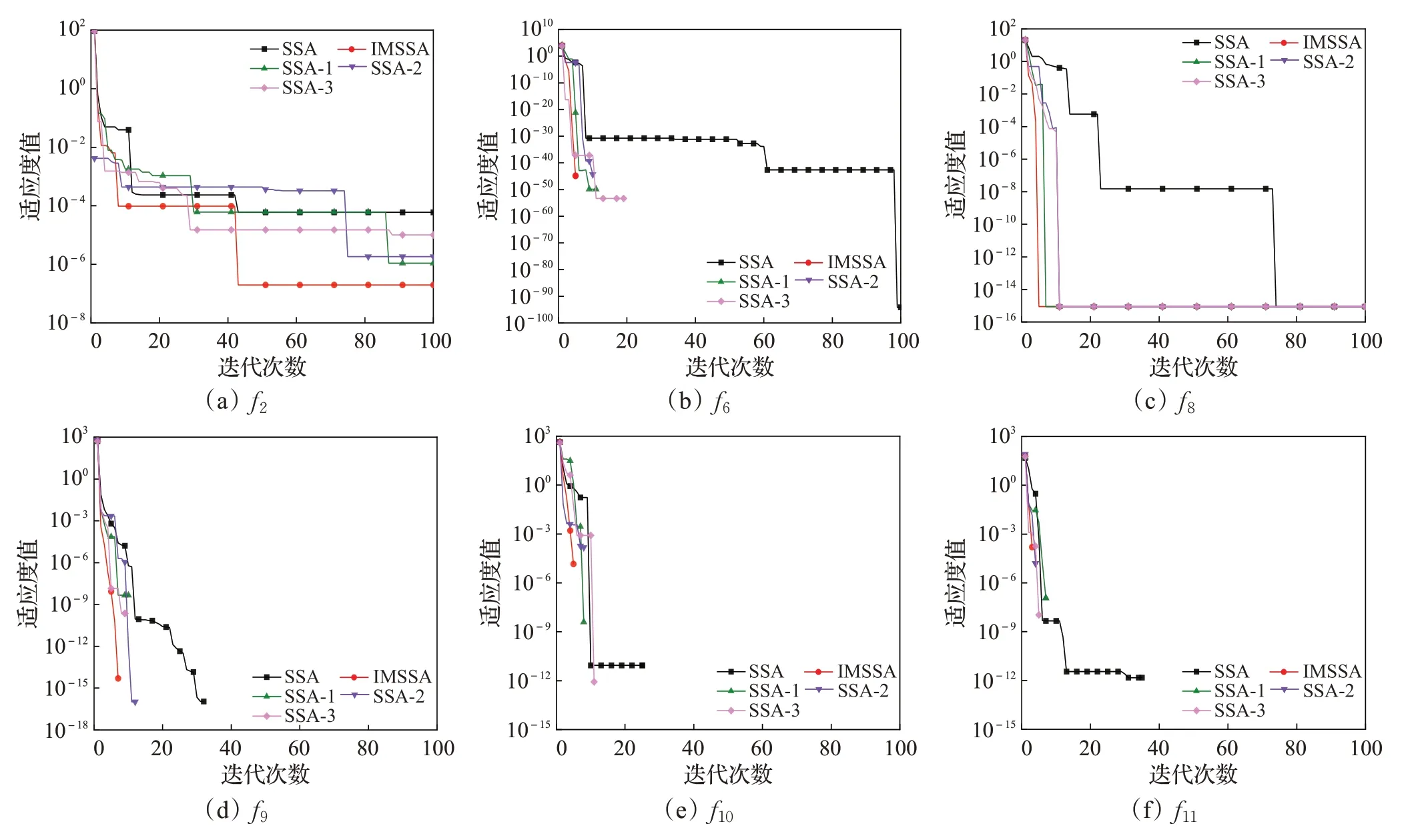
图7 部分测试函数收敛曲线图Fig.7 Convergence curves of partial test functions

3.7 Wilcoxon秩和检验

为了更加全面地检验算法性能，本文引入Wilcoxon秩和检验[25]对文中50次独立运算下的IMSSA算法与其他六种算法的最佳结果进行显著性检验，检验是否存在显著性差异，判断可靠性。原假设H0为：两种算法数据不存在显著差别；备选假设H1为：两种算法数据总体的差别显著。利用检验结果p值来比较两种算法是否存在差异，当p ＜0.05 时，拒绝H0假设接受备选假设H1，说明两种算法之间存在显著差别；当p ＞0.05 时，接受H0假设，说明两种算法寻优性能相当。

由于IMSSA不能与自身进行比较，将IMSSA与SSA、SCDLPSO、GA、GSO、COGWO、NLKH 进行比较，其中N/A表示相应算法在秩和检验中性能相当，“+/=/-”表示IMSSA 的性能优于、相当于和劣于所对比的算法。通过分析表6中的结果可以发现，在IMSSA与SSA对比的f5、f8～f10函数中，IMSSA 的性能与SSA 相当，这是因为SSA本身寻优性能较好，IMSSA与SSA皆能寻得最优解，只是IMSSA寻优性能提升不明显，不过胜在收敛速度较快，稳定性好。在测试函数f5中，IMSSA与COGWO的显著差异性不明显，优化性能相当。其余的p值基本都小于0.05，表明该算法的性能在统计上是显著的，从而表明IMSSA比其他算法拥有更好的优越性。

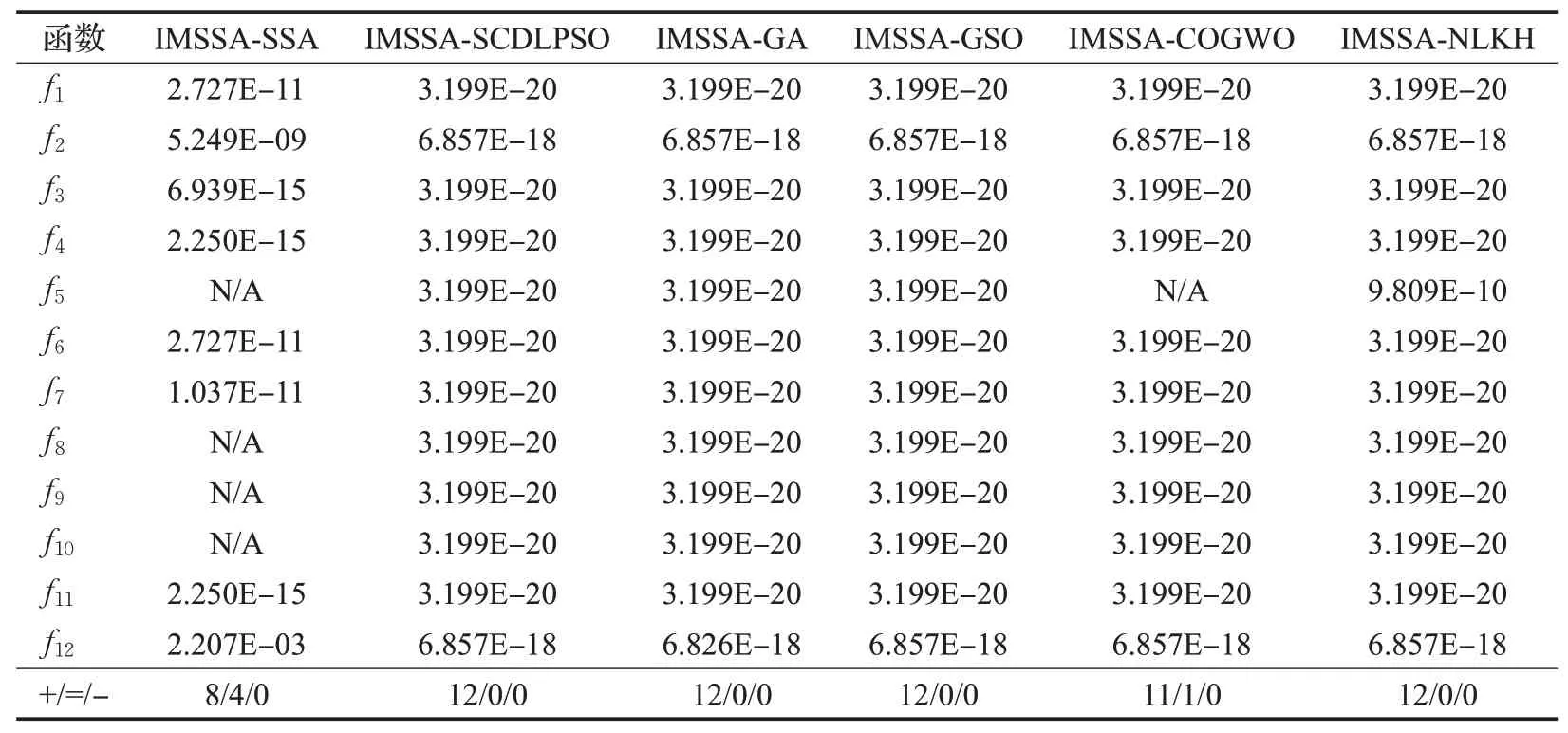
表6 Wilcoxon符号秩和检验结果Table 6 Wilcoxon signed rank sum test results

3.8 时间复杂度分析

设N为种群规模，D为空间维度，itermax为最大迭代次数，种群参数初始化时间为t0，每一维生成随机数的时间为t1，求解适应度值的时间为f(D)，将所有麻雀个体的适应度值进行排序的时间为t2，则基本SSA整体进行初始化的时间复杂度为：

在探索者阶段，麻雀种群中探索者的数量为r1N，r1为探索者比例，探索者适应度值计算时间为f( )

D，根

据式（1）更新探索者位置的时间为t3，两个随机参数Q和α产生的时间均为t4，则该阶段时间复杂度为：

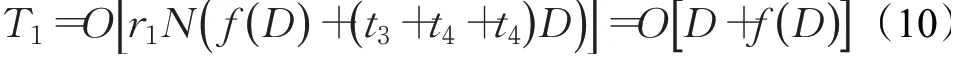
在跟随者阶段，麻雀种群中跟随者数量为(1-r1)N，计算跟随者适应度值的时间为f(D)，由式（2）更新跟随者位置的时间为t5，一个随机参数Q产生的时间记作t6，则该阶段时间复杂度为：

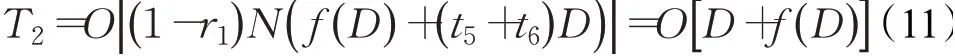
在警戒者阶段，麻雀种群中警戒者的数量为r2N，r2为警戒者比例，每一维按式（3）进行位置更新的时间为t7，两个随机参数β和K产生的时间均为t8，则该阶段时间复杂度为：

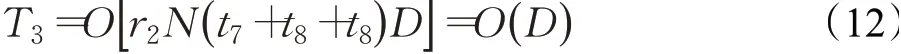
综上，基本SSA算法的时间复杂度为：

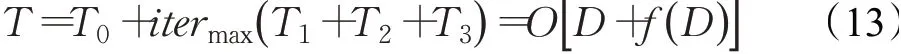
在改进算法（IMSSA）中，种群参数初始化时间为η0，根据式（4）和式（5）进行初始化种群位置的时间为η1，每一维生成随机数的时间为η2，求解适应度值的时间为f(D)，将所有麻雀个体的适应度值进行排序的时间为η3，则IMSSA整体进行初始化的时间复杂度为：

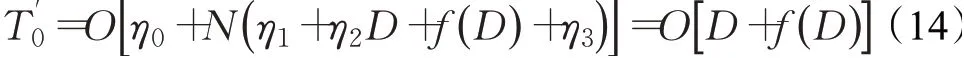
在改进后探索者阶段，麻雀种群中探索者的数量为r1N，根据式（6）产生惯性权重的时间为η4，探索者适应度值计算时间为f(D) ，每一维根据式（7）更新位置的时间为η5，两个随机参数α和Q产生的时间均为η6，地图罗盘算子产生的时间为η7，则该阶段时间复杂度为：

在改进后跟随者阶段，麻雀种群中跟随者的数量为(1-r1)N，探索者适应度值计算时间为f(D)，每一维根据式（8）更新位置的时间为η8，一个随机数Q产生的时间为η9，则该阶段时间复杂度为：

综上，IMSSA的时间复杂度为：

可见，IMSSA与SSA的总体时间复杂度相同，说明本文提出的改进策略不会增加SSA的时间复杂度。

3.9 SVM优化对比实验

支持向量机（support vector machines，SVM）中惩罚参数和核函数参数的取值对SVM的分类准确率有重要影响[26]。因此，利用SSA、IMSSA、SCDLPSO、COGWO和NLKH 这五种性能较好的算法优化惩罚因子和核函数参数，并建立相应的SVM 轴承故障诊断模型对样本进行分类。通过分类结果的准确程度反映改进算法在实际应用中的效果。本文采用美国凯斯西储大学滚动轴承数据中心提供的型号为SKF6205-2RS 的深沟球轴承驱动端数据进行仿真实验[27]。滚动轴承四种运行状态类型的标签和240个样本划分如表7所示。

表7 实验数据说明Table 7 Experimental data description

由分类结果图8～图12可以看出，SCDLPSO-SVM、NLKH-SVM、COGWO-SVM、SSA-SVM和IMSSA-SVM模型的轴承故障分类准确度依次为86.667%，90.000%，93.333%，95.000%，98.333%。相较于4 个对比模型，IMSSA-SVM 模型对于轴承故障诊断的准确率更高，更具优越性。

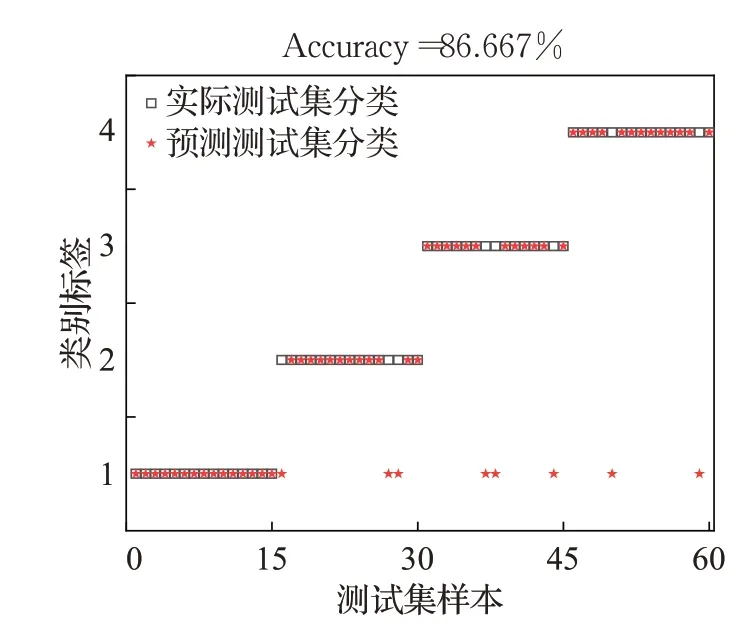
图8 SCDLPSO-SVM分类结果Fig.8 Classification results of SCDLPSO-SVM

图12 IMSSA-SVM分类结果Fig.12 Classification results of IMSSA-SVM

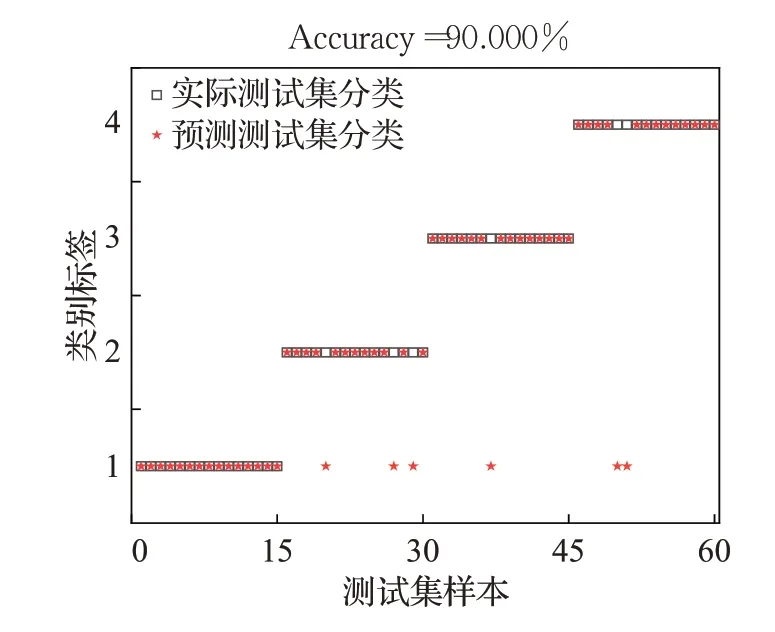
图9 NLKH-SVM分类结果Fig.9 Classification results of NLKH-SVM

图10 COGWO-SVM分类结果Fig.10 Classification results of COGWO-SVM

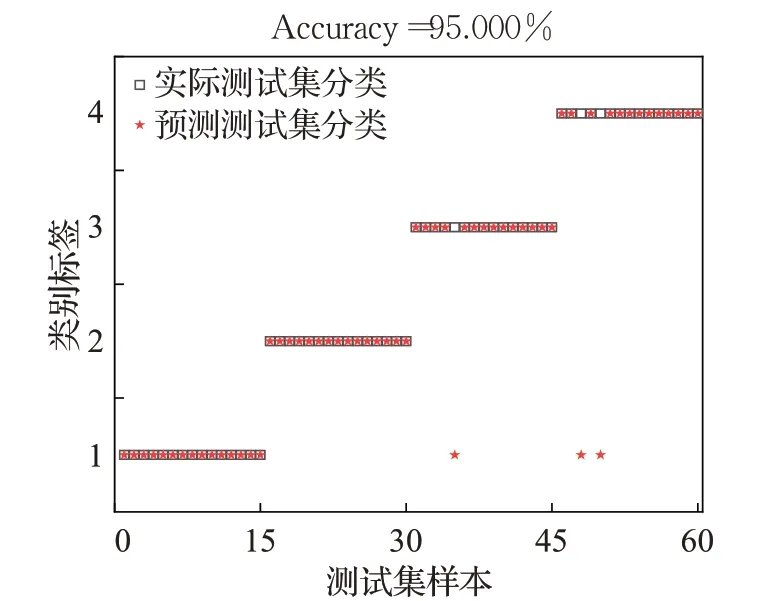
图11 SSA-SVM分类结果Fig.11 Classification results of SSA-SVM

4 结束语

本文提出了一种多策略混合的改进麻雀搜索算法（IMSSA）。首先，采用Sine混沌映射初始化麻雀个体位置，丰富种群多样性，解决种群分布不均匀、搜索空间不足等问题；其次，在探索者阶段引入带有惯性权重的多样性全局最优引导策略来引领种群寻找最好的食物源，平衡算法的全局探索与局部开发能力，加快收敛速度；最后，在跟随者阶段采用双样本学习策略使算法跳出局部最优，进一步提高麻雀种群的搜索能力。通过12 个测试函数进行仿真实验，同时选取了两个最新改进的麻雀搜索算法进行寻优对比，结果证明IMSSA 算法与其他算法相比各项性能均有明显提高。再通过各策略对比实验、Wilcoxon 秩和检验和时间复杂度分析，进一步证明了本文采用的改进策略是有效可行的。最后，验证了经IMSSA 优化后的SVM 轴承故障诊断模型在实际应用中的效果，实验表明IMSSA-SVM模型的准确率高达98.333%，具有一定的应用价值和优势。