基于离散小波变换的数字音频水印技术研究

温 雪

（青岛酒店管理职业技术学院 山东 青岛 266100）

0 引言

传统的数字音频水印处理，多是通过单质定向水印或者面积性水印来实现的，这种方式虽然可以完成预期的处理目标，但实际上在这个过程中，常常会出现水印混乱、层次不清晰或者音频损坏等问题，会极大地影响水印制作的效果[1-3]。因此，需要对基于离散小波变换的数字音频水印技术进行研究和分析，实现水印技术的优化、完善。考虑到最终处理结果的稳定性和可靠性，本文会选择在较为真实的环境之下，结合离散小波变换技术，以传统的处理标准为基础，构架更加灵活、多变的水印嵌入结构，在执行时，提取对应的水印问题，制定具有针对性的解决方案，合理均衡地消除存在的矛盾，实现空间数字音频水印转换，提升整体的水印抗信号处理能力，为后续水印的维护以及压缩提供更加合理的依据[4]。

1 离散小波变换下数字音频水印技术探析

1.1 数字音频水印感知预处理

利用小波变换技术，在音频内部形成一种自由转换模式，获取表征信号以及尺度域，促使音频的水印时域化，此时，将原始的音频进行小波变换，并计算出给定阈值，具体见公式1：

公式1 中：Y表示给定阈值，c表示重构距离，i表示转换序列范围[5]。通过上述计算，最终可以得出实际的给定阈值。根据得出的给定阈值，更改调整原音频中的小波变换重要系数，形成初始水印信号，将区域内的信号压缩成灰度嵌入包，发送到预设的音频处理地址[6]。然后，划定水印小波变换系数具体的嵌入位置，实现逆变换，完成数字音频水印感知预处理，为后续的水印嵌入奠定基础。

1.2 自适应嵌入目标设定

为了提升水印嵌入的贴合度，可以在预设的嵌入范围之内，假设原音频信号为单向指令协议，在区域之内设定对应数量的嵌入节点，计算出单向嵌入幅度值，具体见公式2：

公式2 中：W表示单向嵌入幅度值，j表示嵌入方向，N表示进制处理常数。通过上述计算，最终可以得出实际的单向嵌入幅度值[7-8]。在音频灰度处理中，在单向嵌入幅度值基础上作出对应调节，采用DCT 动态压缩执行处理技术，构建自适应量化嵌入范围，并计算出DCT 变换系数，具体见公式3：

公式3 中：K表示DCT 变换系数，T表示量化距离，R表示低频极限值。通过上述计算，最终可以得出实际的DCT 变换系数[9]。根据自适应的嵌入方式，划定小波变换的实际环节，将音频中的4 个低频AC 分量逐渐转换为8位的高频，形成动态自适应嵌入目标。

1.3 音频信号分段处理及嵌入重组

音频信号分段处理及嵌入重组，主要是对音频水印嵌入的分段处理。传统的嵌入会以综合复制的方式实现内部嵌入，但是这种方式一直存在弊端，很容易出现大面积的水印混乱。所以，需要进行一定的整改和调整。采用逆向处理法先将数字音频信号依据特征作出分段，并设定嵌入水印内部信息的执行协议，确保数字水印的透明度以及鲁棒性，单个音频的处理长度为6 为宜[10]。后续在每个音频段之中嵌入3 个单向比特水印信息，并构建具体的分段处理、重组结构，具体见图1。

根据图1，可以完成对音频水印嵌入分段处理、重组结构的设计。

1.4 音频离散加密变换处理

结合离散小波变换技术，进行音频离散加密变换处理。在目标音频段之中，选取一个核心嵌入点，制定变换信号，设定离散波动范围，形成动态加密嵌入原理，以金字塔的形式，布设对应的信号，假设二维信号子带分别是IL1、LH1、HL1 和HH1 上的双向变换系数，完成对音频水印嵌入信号金字塔处理结构的设计和构建。利用离散小波变换技术，对基础音频段作出二维信号高通和低通滤波处理，从多个方向，对HH1 的音频特征以及水印格式作出修改，核定实时的转换系数，一般需要控制在0.45～0.85之间即可。

根据人类视觉和听觉的需要，构建离散平滑水印的格式，并在嵌入区域设定加密协议，确保二通道滤波嵌入处理处于正交状态，可以在提升整体水印识别率以及加密程度同时，实现多方向的音频离散加密变换处理。

1.5 离散小波变换嵌入模型设计

设计离散小波变换嵌入模型，对音频中每一个水印的嵌入点进行定位，从鲁棒性的角度出发，核定嵌入的自适应路径，在加入水印的整个过程中，将原始音频的嵌入局部特征调整为重合整体特征，并逐渐增加入水印的强度，与此同时，对此时音频的小波变换状态做出引导与调整，形成基础嵌入建模。对音频段实时嵌入效果进行衡量，扩大具体的嵌入范围。

采用DWT 方法更改离散小波的变换频率，在对应的嵌入子带之上，对嵌入的水印信息压缩，传输至对应的叠加地址中。但是需要注意的是，部分的离散波段是动态的，并不固定，所以，获取的数据也并不精准。可以标记逆变系数，划定具体的嵌入范围，在频域和时域中同时形成小波变换叠加，在模型中形成比照标准，完成对小波变换叠加比照标准的设定与效果的呈现。将获取的数据以及标准设定在模型之中，增设对应的侵入模块，形成逆变处理嵌入模式，最终完成离散小波变换嵌入模型的设计。

1.6 Fibonacci 小波逆向置换法实现数字音频水印处理

采用Fibonacci 小波逆向置换法来最终实现数字音频水印处理。这部分可以采用置乱分散比特嵌入划分的形式来实现，可以预先划定具体的鲁棒处理范围，在离散波段的变化区域之内，对目标音频作出Fibonacci 变换预处理。

将逆向嵌入周期更改为2 或4，根据嵌入的途径，使水印均匀分散布设在数字音频之中，在确保标记的同时，还可以最大程度提升数字音频的安全性与稳定性，降低水印处理的误差与缺陷，减少破损以及残缺等水印问题。在等效变换的环境之下，形成稳定、安全的嵌入处理效果，增加嵌入的清晰度与持续性，最终通过Fibonacci 小波逆向置换法实现数字音频水印的最终处理。

2 方法测试

本次主要是对离散小波变换下数字音频水印技术的实际应用效果进行分析与研究。选取一段标准的数字音频A作为测试的主要目标对象，将A 音频均等地划定为3 个阶段。考虑到最终测试结果的精准度、可靠性，测试以较为真实的环境为背景，以比照的形式展开。选择3 种方法在相同的环境之下同时展开测试，第1 组为传统的时域数字音频处理方法，将其设定为传统时域数字音频处理测试组；第2 组为传统的自适应音频处理方法，将其设定为传统自适应音频处理测试组；第3 组为本文所设计的音频处理技术，需要设定为离散小波变换数字音频测试组。最终得出的结果对比分析，接下来，需要搭建相关的测试环境。

2.1 测试准备

在对离散小波变换下数字音频水印技术的实际应用效果进行分析与研究之前，需要先搭建相应的测试环境。利用专业的处理仪器，对目标A 音频进行基础性的处理和识别，并获取音频的灰度值，具体见公式4：

公式4 中：H表示音频灰度值，t表示水印进制距离，y表示逆向处理范围。通过上述计算，可以得出实际的音频灰度值。此时，将原始音频依据特征划分为不同的阶段，结合离散小波变换技术，构建3L+1 子带，并预设基础的指标参数，具体见表1。

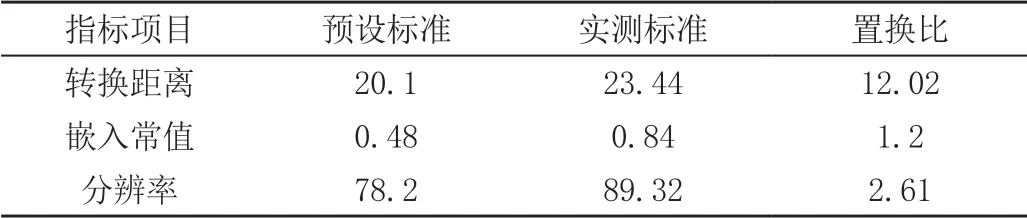
表1 基础数字音频水印指标参数预设表

根据表1，可以完成对基础数字音频水印指标参数的预设。随后，在目标音频A 中，对水印图像进行置乱，随机生成子集矩阵，并计算数字音频的水印重复比，具体见公式5：

公式5 中：U表示数字音频的水印重复比，e表示随机嵌入点，m表示波动系数。通过上述计算，可以得出实际的数字音频水印重复比。在矩阵中设定对应的嵌入节点，结合重复比，划定对应的处理区域，并分设逆变离散距离。

以此为基础，采用离散小波变换处理，将每一个节点与矩阵形成关联，获取首批水印处理数据，做好记录。随即在预设的小波系数矩阵之中，测定水印强度因子，计算出抗压强度值，具体见公式6：

公式6 中：B表示抗压强度值，x表示强度因子，f表示小波转换比。通过上述计算，可以得出实际的抗压强度值，对A 音频覆盖区域明确划定。核定测试的设备与装置是否处于稳定的运行状态，同时确保不存在影响最终测试结果的外部因素，核定无误后，开始具体的测试。

2.2 测试过程及结果分析

在上述搭建的测试环境之中，结合离散小波变换技术，对目标A 数字音频进行水印嵌入处理。根据小波变换的实际状态，获取基础水印数据，识别描绘嵌入的过程，具体见图2。

根据图2，可以完成对识别描绘嵌入过程的构建与状态把控。在音频处理中，对于水印的嵌入一般是单向的，会采用特定的格式实现，但是这种方法的效果并不好，对于后期的维护和调整也会形成不同程度的阻碍。

将目标音频进行二次嵌入处理，对音频中的嵌入强度因子作出识别，促使水印经过小波变换后自身的高频系数逐渐发生变化，由低至高逐步攀升，而此时音频的水印嵌入已经完成应变标记，确保低频系数在89%以上，高频系数在97%以上即可。依据原始音频小波系数的特征量，控制水印的嵌入强度，通过计算出实际的鲁棒系数来验证具体的处理效果，见表2。

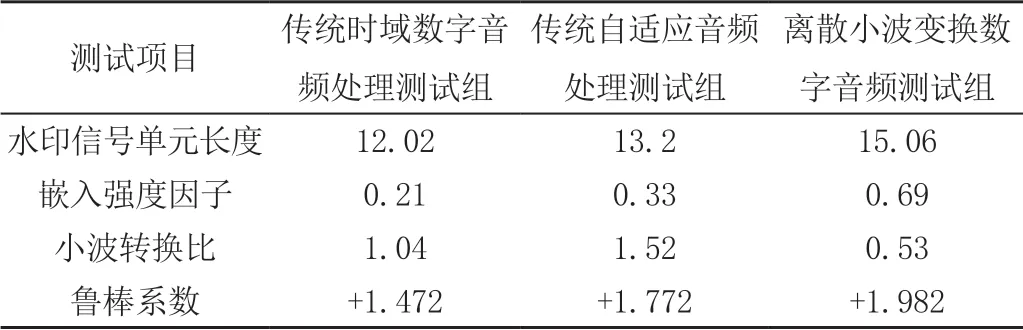
表2 测试结果对比分析表

根据表2，可以完成测试分析：与传统时域数字音频处理测试组以及传统自适应音频处理测试组相对比，本文所设计的离散小波变换数字音频测试组最终得出的鲁棒系数相对较高，并控制在合理的范围之内，表明对于水印的嵌入误差较少，效果更佳，具有实际的应用价值。

3 结语

综上所述，与传统的数字音频水印方法相比，本文所设计的处理模式，以离散小波变换技术作为辅助支持，营造更加稳定、安全的处理环境，并构建灵活的水印制作方法。在复杂的处理环境中，还需要加强对音频嵌入数据的核定以及计算，提升综合精准度，在合理的范围之内，扩大水印覆盖的区域，根据特定的层级，形成具体的水印样式，为相关技术和行业的进一步发展奠定更为坚实的基础条件。