新课程背景下高中数学变式题设计方法探析①——以“数形结合思想在函数问题中的应用”一课教学为例

马艳波

（延边州教育学院，吉林 延吉 133000）

高中数学新课程基本理念是：高中数学课程以学生发展为本，落实立德树人的任务，培养科学精神和创新意识，提高升数学学科核心素养。高中数学课程面向全体学生，实现：人人都能获得良好的教育，不同的人在数学上得到不同的发展。

数学作为基础学科，由于它抽象，思维严密，逻辑严谨，知识之间联系紧密，环环相扣，对学习者逻辑思维有很高的要求，所以，学生对它又爱又恨。逻辑思维能力强的人喜欢数学，他们享受问题被攻破以后那种成就感，自豪感，这些学生通过数学的学习，增强了自信心和学习上获得的幸福感，所以爱它；相反，学习者如果空间想象力或者逻辑思维能力差，那么数学对于他们就像天书一样，题干中短短几行字，寥寥几个字母就能让人费尽心思，绞尽脑汁。从哪入手？怎么想？为什么这么想？学习者感到非常困惑。作为教师，以答疑解惑，育人为根本，教给他们知识，教会他们学习，是每个教师的愿望。那么，怎样设计实施教学方案，才能使每个学生都得到不同程度的发展？笔者认为，对于数学来说，变式教学是一种尤为重要的教学方法。

以高三专题复习之《数形结合思想在函数问题中的应用》一课为例，谈一下如何进行教学设计，才能符合新课程教育理念。本节课采用了变式教学，整节课以变式题为线索，引导学生梳理何为“数”，怎样定“形”，以及何时使用“数形结合”，怎样使用“数形结合”等，思维上有梯度，让不同层次的学生都会在课堂上有收获。

一、通过变化问题的表达形式设计变式，实现多题归一，夯实数学基础

通过变化问题的表达形式设计出来的变式，可以帮助学生从多角度探索同一类问题的解题策略，借助于等价转化实现多题归一。在实际操作过程中，可以考虑设计具有等价关系的变式，对一类问题进行规律总结。同时,因为这类变式虽然引导学生多角度观察，但却只需要解决一个问题，这就大大地提高了课堂效率。

比如，在《数形结合思想在函数问题中的应用》一课中，教师可设计问题探究，以五个具有等价关系的变式作为一节课的开篇：

教师以等式“loga x=4x”为原型，不断变化形式，设计出问题探究1 中的1 题到5 题共五个小问题。表面上看是五道不同的题，而且题的难度逐渐加大，但学生分别用移项、提取公因式、消元、换元、配方等常见的运算手段进行变形整理，就会发现四个问题都还原为方程“loga x=4x”有解的问题。所以只需在同一个坐标系中画出y=logax和y=4x函数图象，观察交点位置即可。

这样的设计可以让学生了解到很多看似复杂的问题，只要通过变形、化简、整理，就可以将问题大大简化，问题变得简单，很容易找到问题的实质。通过该题的设计，又可以让学生体会到“数学运算”是“数形结合思想”中的“数”众多表现形式中最重要的一种，这种设计发展了数学运算的核心素养，同时，将四个问题归结为一个问题，教师只需引导学生分析出问题的实质，解决起来不会占用太长的课堂时间，不会出现“本末倒置”的状况。

二、通过转变问题的陈述方向设计变式，揭露问题本质，渗透数学思想

通过转变问题的陈述方向设计出来的变式，学生会感受不同陈述方向下相同的问题本质，可以充分体验多题一解，收敛数学思维。而在探索、发现，探寻解题方法的过程中，也会潜移默化地渗透转化与化归、数形结合、函数与方程等数学思想。

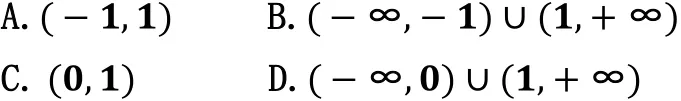
例1.（2020 北京卷6 题改编题）方程2x+x −1=0的根有__________个。

2020 北京卷6 题求不等式的解集，与2020 北京卷6题相比较，例1 改变了所求问题，由“不等式的解集”变为“方程的根的个数问题”。学生对方程的根，不等式的解集，函数零点三者的关系并不陌生，三者表现形式不同，但实质是一样的，是函数的几种不同求解方向，其实质就是利用函数解决问题。对于这样的问题，如果从已知的角度不好求解，我们可以换一个角度去考虑它。但在求解过程中，函数的选择对解题的难易程度有影响，所以，数形结合法解题时，所选择的函数一定是容易画出图象的。

比如例1，我们可以把它看成y=2x-1与y=-x的交点问题；也可以把它看成y=2x与y=-x+1的交点问题，绝不能看成y=2x+x与y=1交点问题。

这样的变式有利于学生进一步理解概念。在例1 的基础上进一步变式，由不含参数问题拓展到含参数问题,题的难度加大，构造函数的类型变多，解法也增多。课堂教学中，教师放开手，让学生就这两道题进行再变式，使问题不断拓展，加深学生对问题的理解，思维能力不断提升。

三、通过更改问题的等量关系设计变式，挖掘知识内涵，发散数学思维

通过更改问题的等量关系设计出来的变式有两种：一种是从等式到不等式的变式，一种是从不等式到等式的变式。这类变式被广泛地应用在课堂教学中，学生在解决完一个等式问题后，教师将等号变为不等号，抛出一个不等式问题，可以深入挖掘知识内涵，延展解题思路，发散数学思维。

《数形结合思想在函数问题中的应用》一课中两次使用这种变式：

例1：方程2x+x −1=0的根有__________个。

一次是例1 改变了2020 北京卷6 题所求问题，由“不等式的解集”变为“方程的根的个数问题”，再一次是不等式到等式的变式。解方程与解不等式相比较，学生更了解方程问题。就本题而言，等号左侧的函数是单调递增的，且当x 趋向正负无穷大时，函数可正可负，所以有一个根。这种方法只需观察，不需计算，非常容易求解。这样做的目的是让学生从熟悉的问题入手，解题思路要开阔，不拘泥于某一种解法，符合学生的思维逐层深入的思维过程。这样的变式可以让一道题的解法增多，增加学生的入手点，增多问题的解题方向。学生既可比较两种方法的优劣，又可以体会“数形结合思想”既不万能，也不是解题的唯一方法。

问题探究：

教师在《数形结合思想在函数问题中的应用》一课中，在得到等式问题的解题策略之后，再重新解决问题探究1的第1 个小题，并将等式问题变式为不等式问题，数学思维过渡自然，自然而然地联想到用图象方法解决不等式问题。有效实现了不同层次的学生逐渐进入思维深度。

四、通过隐匿问题的几何背景设计变式，拓宽审题视角，发展直观想象的素养

通过隐匿问题的几何背景设计出来的变式，学生需要从代数表达式出发联想其几何意义，构造几何模型，将代数问题转化为几何问题求解。这类变式可以拓宽审题视角，发展数学建模、直观想象等数学核心素养。

例2.（2020 北京卷6 题）已知函数f （x）=2x−x −1，则不等式f （x）＞0的解集是（ ）。

变式1.若对任意的x，不等式ex−x −k ＞0恒成立，求k的取值范围；

变式2.对于任意的x1、x2，求的最小值；

这三道变式题看起来有一定难度，变式题之间看似毫不相干，部分学生看到以后不知如何入手。其实，它们都是教师针对例2（即：2020 年北京卷的第6 题）进行的变式。它们在解题思想上是紧密相连的，层次递进，难度逐渐加大。变式1 由例2 中不含参问题变形为含参问题，将变成，学生根据例1 的讲解很容易找到解法，教师也可以适时地让学生自己编题，开拓学生的思维；第二次变2x式将变e式x1 的问题等价转化为y=ex图像上的点到函数图像上的点距离最小值，并将这个问题隐藏在函数表达式之中。由刚刚做过的变式y=1x学生知道，只需将变式1 中的k 看成0 即可；第三次变式是对变式2 解题思路的变式，用数形结合法求解，变式3 可以看成两点（cosx,sinx）与(2,0)连线的斜率；变式3 解法不唯一，教学时 可以多种方法求解。教师通过这种变式设计引领学生从几何意义角度思考问题，有效地实现“数”与“形”的统一，发展了直观想象的数学核心素养。

总之，合理使用变式题无论是对于帮助学生实现规律的总结，还是对解题方法的探索与发现都极具好处,同时也可以帮助学生逐步实现思维的深入，培养学生发现问题、分析问题、思考问题直至解决问题的学习习惯。当然，变式题的选择贵在精，而不在多,需要教师严格筛选，合理变式，以便更好地提高课堂教学效率。