一道教材习题的变式
⦿西华师范大学数学与信息学院
王小梅
1 引言
习题是教科书的重要组成部分,具有一定的典型性与示范性,很多高考题就来源于教材的习题.教师应当充分发挥教材习题的功能,合理运用例题、习题.基本不等式是高中数学的重要知识,在最值问题中发挥着重要作用.但由于基本不等式的灵活多变,学生在学习中难以灵活应用其结论(“积定和最小,和定积最大”)解决最值问题,因此,有必要对其深入研究.而“变式训练”为此提供了一个很好的突破口.对教材习题进行变式,一方面,加深学生对数学知识的理解,有助于学生发现数学问题的本质;另一方面,提高学生解题能力,达到举一反三的效果.与基本不等式有关的问题很多,本研究将通过教材一道习题的变式加深学生对“积定和最小”这一结论的理解与运用.
2 原题呈现
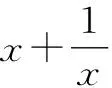
分析:该题是教材的一道习题(解法略),主要是对基本不等式的考查,属于基础题,直接利用基本不等式即可解决,但是不少高考题就源于这道题.另外补充,由基本不等式推广的n元的基本不等式:

3 习题变式
3.1 数量变式
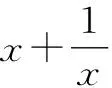

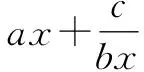
分析:变式1和变式2均是在“量”上进行改变,变式1是改变自变量的范围,变式2是改变式子的系数,式子的结构仍不变,与原题解法一致.需要注意的是,变式1要使用基本不等式,需要满足基本不等式的条件,可通过换元法改变自变量的范围.
3.2 结构变式



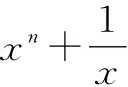



3.3 多元变式
前面所有的题目都只有一个变量,还可以增加变量的个数.



下面一道高考题与之类似.


A.1 B.2 C.3 D.4
变式9已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是.(2020江苏,第12题)
分析:变式6与原题解法一致,只是增加一个自变量;变式7与变式4类似,可通过拆项法进行构造,除此之外,还可两次利用基本不等式解决.需要注意的是,每次使用基本不等式时,取等号的条件不能遗漏,并且所有的条件都要满足.变式8中式子的结构比上述其他题要复杂,不难发现:


3.4 延伸变式
以上变式主要是对基本不等式本身的运用.此外,我们还可以对基本不等式进行延伸,可得到如下推论:

该结论是由重要不等式(a2+b2≥2ab,a,b∈R,当且仅当a=b时,等号成立)变形而来.该结论应用广泛.一方面,能够起到降次的作用;另一方面,将分式不等式转化为整式不等式,使问题得到简化.下面举例说明.
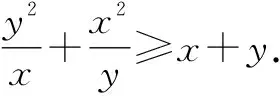
解法1:因为x>0,y>0,所以

=2x+2y,
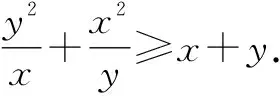
解法2:由推论可得
当且仅当x=y时,等号成立.
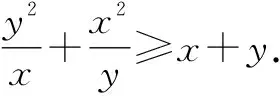
分析:解法1需要构造成恰当的形式,具有一定的技巧性.相比之下,解法2更加自然,实际上就是基本不等式的变形应用.
变式11设a≥b>0,求证3a3+2b3≥3a2b+2ab2.(2009江苏,第21题)
解析:可以看出,式子结构对称,左右两边次数不同,可利用前面的结论进行降次.首先,两边同时除以ab,那么,只需证
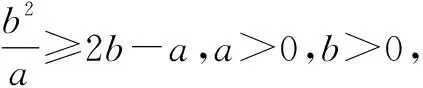
又因为a≥b>0,所以4a+b≥3a+2b.

所以,3a3+2b3≥3a2b+2ab2,得证.
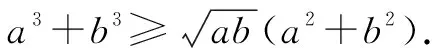
解析:为了简化不等式,可平方去根号,得
a6+b6+2a3b3≥ab(a4+b4+2a2b2).
当a>0,b>0时,与变式11类似,两边同除以ab,只需证


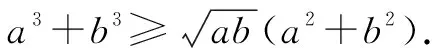
当a,b至少一个为0时,所证不等式也显然成立.
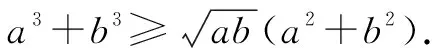
4 总结
从上述分析可以看出,利用基本不等式解决相关问题可用换元法、构造法,通过拆项或添项构造出“积定”的形式.一系列的变式题也充分体现了化归思想在解题中的应用,可以将分式化为整式,二元化为一元,高次化为低次,等等.另外,对教材习题进行深入研究十分有必要,高考题往往来源于教材例题、习题.教师可以通过一题多变,在变换中找不变,引导学生发现数学的本质.

