例谈含参数问题的运算优化策略*
⦿启东市教师发展中心
沈 辉
1 引言
含参数问题主要考查函数的单调性、最值和分类讨论思想,是高考、模拟考试中重要考点.如果方法选择不当,计算起来会比较复杂,甚至做不下去,或出现遗漏等情况.本文主要谈谈几个含参数问题如何回避讨论,或降低讨论难度的方法.
2 运算优化策略
2.1 特殊值法——局部缩小
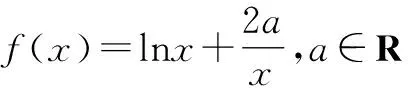
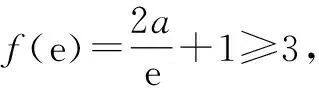
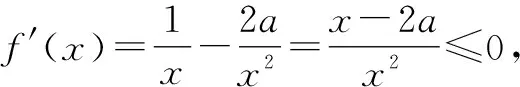
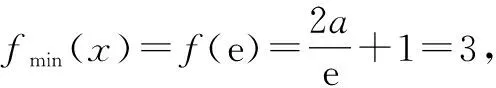
综上得,a=e.
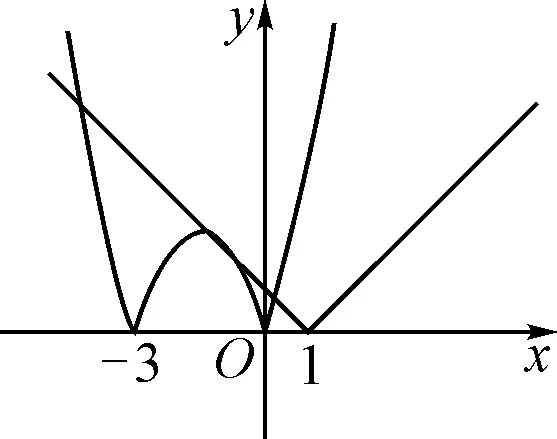
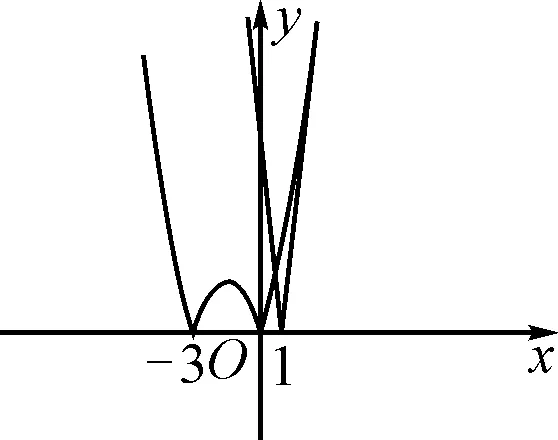
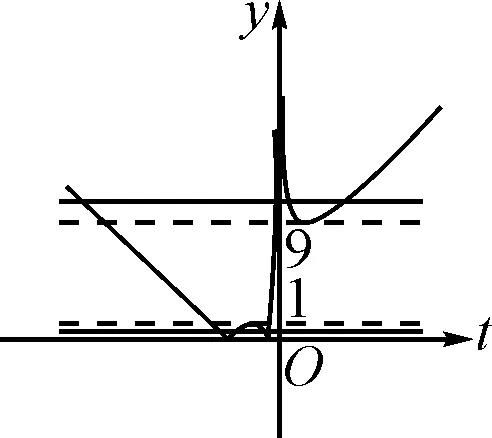
点评:如果由f′(x)的表达式研究函数的单调性讨论其最小值,则需分①2a≤1,②1<2a 例2(2008年江苏高考卷第14题)f(x)=ax3-3x+1对于x∈[-1,1]总有f(x)≥0成立,则a=. 解析:由f(1)=a-2≥0,f(-1)=-a+4≥0,解得2≤a≤4. 故a=4. 点评:本题若化为fmin(x)≥0,但在求f(x)的最小值时需要对a分大于、等于、小于0三种情况讨论,计算繁琐,小题大做.利用上述特值限定参数范围,则无需讨论,简洁明快. 方程有解(函数存在零点)、不等式恒成立、不等式存在性等含参数问题,很多情形下可以把参数和变量分离,将式子变成其中一边不含参数的形式,从而避免讨论. 例4(2014年江苏卷第19题第Ⅱ问)已知函数f(x)=ex+e-x,其中e是自然对数的底数.若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求实数m的取值范围. 解:由mf(x)≤e-x+m-1,得m(ex+e-x-1)≤e-x-1. 因为ex+e-x-1≥2-1>0,所以 评注:上述例3、例4两题分别是含参数的方程有解问题和不等式恒成立问题,采用参变量分离法,避免了分类讨论. 例5(2012年浙江理第22题第Ⅱ问)已知a>0,b∈R,函数f(x)=4ax3-2bx-a+b. 证明:当0≤x≤1时,f(x)+|2a-b|+a≥0. 分析:要证f(x)+|2a-b|+a≥0,即证4ax3-2bx+b+|2a-b|≥0.注意到不等式左边含有x,a,b三个字母,如果把它们看成地位相当的三个变量,几乎无处发力,很难展开研究.所以需要根据题目结构特征,人为划分主从地位,选择适当变量作为主元.本题如果将x看作主元,字母a,b当作参数,则不等式左边是一个关于x的三次函数,研究起来较繁.换一个研究视角,将字母b看作主元,这样不等式左边就是一个关于b的一次分段函数,且每段的单调性很容易得出.选择字母a为主元,虽然也是一次分段函数,但每段的单调性还需讨论. 又a>0,故gmin(b)≥0,即4ax3-2bx+b+|2a-b|≥0得证. 例6( 2014年江苏苏北四市二模15)设函数f(x)=log4(4x+1)+ax(a∈R).若不等式f(x)+f(-x)≥mt+m对任意的x∈R,t∈[-2,1]恒成立, 求实数m的取值范围. 分析:本题含有x,m,t三个字母,如果视三个字母地位相等,平均使用力气,则无助于解决问题.读题后发现,可以先把x看成变量,m,t看成常量,逐个击破. 解:设g(x)=f(x)+f(-x)=log4(4x+4-x+2)≥log44=1,则由题意得mt+m≤gmin(x)=1. 所以,问题转化为“mt+m≤1 对∀t∈[-2,1]恒成立,求m的取值范围”.这时,就可以把t看成变量,把m看成参数,则把mt+m≤1看成关于变量t的一次函数(m≠0时) . 评注:解答上述一类含多个参数的问题,关键是对变量和参数关系的转换.而变量和参数是相对的,在一定条件下可以相互转换,需依次进行,逐次变化,体现了事物是联系、变化、发展的辩证观. 有些含多个参数的分类讨论问题,如果是从局部出发,看成是几个不相干的变量来处理,则难以奏效或计算冗繁.因此,需要调整视角,把一些关于多个变量的代数式作为一个有机整体,对整体结构进行全面深刻地分析改造,找到解决问题的途径和办法. 分析:根据两点之间线段最短,可以得到a,b,c之间满足一些不等关系,利用这些不等关系,逐步缩小,最后化成一元问题解决. “数缺形时少直观,形缺数时难入微”.在含参数问题的处理中,如果从“数”的角度解答困难,不妨转换角度,从“形”入手,根据数的几何意义,画出图形,数形结合的思想往往能起到重要的作用,便于解答. 例8(2014年天津第14题)已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为______. 解析1:显然a>0. 如图1,当y=-a(x-1)与y=-x2-3x相切时,a=1,此时f(x)-a|x-1|=0恰有3个互异的实数根. 图1 图2 如图2,当直线y=a(x-1)与函数y=x2+3x相切时,a=9,此时f(x)-a|x-1|=0恰有2个互异的实数根. 结合图象可知,a的取值范围是(0,1)∪(9,+∞). 图3 含参的数学问题是高中各级各类考试中常见的题型,解决的通法是对参数的取值进行分类讨论.但有时候通过分类讨论去解决,情况多,计算量大,学生解答思维混乱,容易卡壳或算错.上面探讨了几种转化方法优化运算解决参数问题的策略.因此,在让学生掌握通性通法的基础上,还要教会学生根据不同的条件具体分析,充分理解参数的意义及参数与主元的关系,对症下药,找出灵活有效的解决办法.
2.2 参变分离——避免讨论
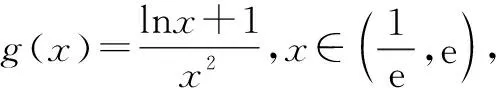
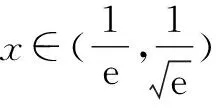
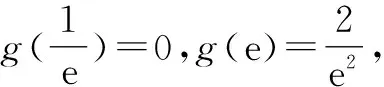
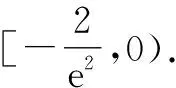
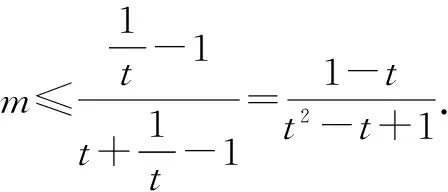
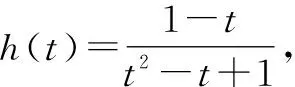
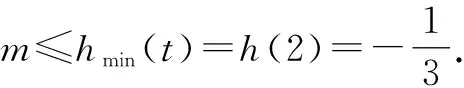
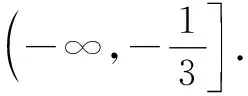
2.3 转换视角——选择主元
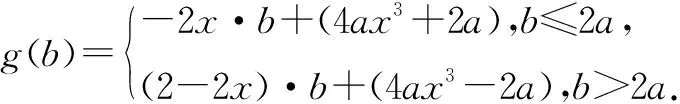
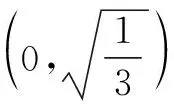
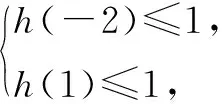
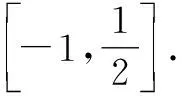
2.4 整体思想——消元减参
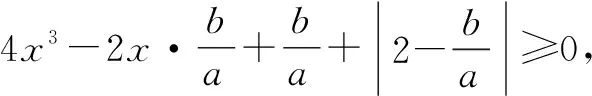
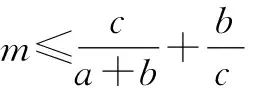
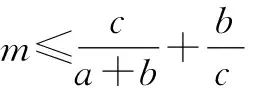

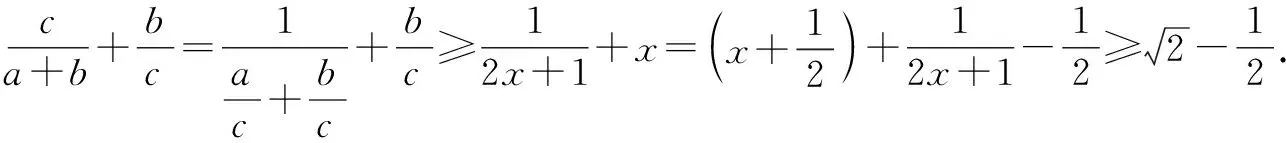
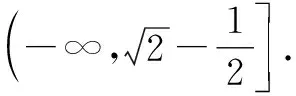
2.5 数形结合——形象直观
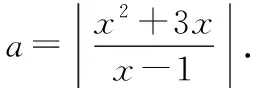
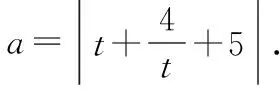
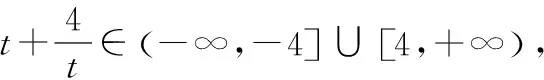
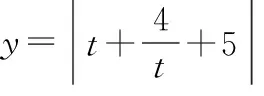
3 结语

