基于改进西原体模型的岩石流变特性分析

朱帅，李明飞，姜丽萍，窦益华，王智勇

1.陕西铁路工程职业技术学院（陕西 渭南 714000）

2.西安石油大学 机械工程学院（陕西 西安 710065）

0 引言

岩石的流变包括蠕变、松弛和弹性后效，岩石的流变影响油气井等岩石工程结构的稳定性和安全性，因此，岩石流变特性的研究引起了人们的重视[1-2]。目前岩石流变研究的一般做法是：根据岩石流变的机理，建立描述岩石流变的模型和方程，实验测量模型和方程中的关键参数，再将包含这些参数的模型和方程用于岩石流变分析[3-4]。

目前，不同工程领域的学者结合自身学科特点，有针对性地开展岩石流变特征研究。肖欣宏等人针对水环境下的软岩工程安全问题，研究了低应力作用下的蠕变特性和该特性相同水压条件下的瞬时应变，得出水压高低和应力大小对蠕变特性的影响[5]。刘颖等人从工程施工及运行实际中发现不同含水状态下的岩石蠕变特性问题，对砂岩工程试样进行了蠕变力学试验，对比干燥状态下的砂岩变化得出其受含水量的影响情况[6]。贵州大学的王唯等人为了探索岩石全过程蠕变特性，改进传统的Bingham模型，对比天然页岩蠕变试验结果，验证其模型的适用性和可行性[7]。黄海军对隧道围岩在不同冻融循环次数下的蠕变特性进行试验研究[8]。安徽理工大学的王游等为了克服传统元件模型组合难以对岩石非线性蠕变特性具体描述的问题，改进广义Kelvin 模型进行参数确定和验证，为类似问题研究提供思路和借鉴[9]。很多学者通过改变流变元件组合，改进了岩石蠕变模型以验证具体工程领域的岩石蠕变问题[10-11]。高子璐等人给改进模型的参数反演提供思路和方法[12]。国内外相关专家学者也采用大边界地层条件仿真方法对岩石流变现象进行推演和性能研究[13-14]。复杂的工程背景下岩石的流变特性是复杂多变的，而西原体模型可较好地模拟岩石流变过程中的蠕变阶段，这对研究流变地层岩石变化很有意义。

借鉴先进的研究经验，以流变岩层与井筒的相互作用为工程背景，针对流变岩层与井筒相互作用时的力学行为变化问题，基于改进西原体模型的岩石蠕变，继续探索岩石流变特性的后续松弛过程。

1 岩石流变本构关系及其改进

1.1 传统西原体模型

岩石流变学理论主要研究岩石的应力-应变状态及其随时间增长的变化规律，建立恰当的本构模型显得尤为重要。如图1 所示，传统岩石力学西原体模型包括胡克体，黏弹性体（凯尔文体），理想黏塑性体，能够反映岩石的弹性、黏弹性、黏塑性[1]。

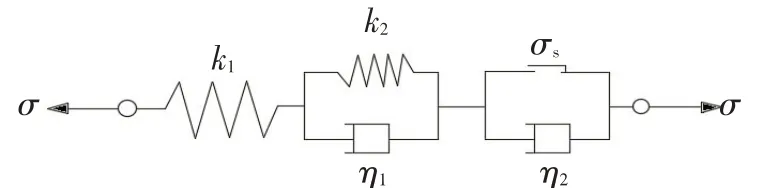
图1 传统的西原体力学模型

文章公式中涉及到的应力单位均为MPa，应变无量纲，时间以d计。图1中，σ为模型应力；ε为应变；σs为岩石的屈服应力；k为弹簧的弹性系数；η为黏性元件的牛顿黏性系数；t为时间。其本构方程和蠕变方程如下[1]：

1）本构方程

当σ＜σs时，

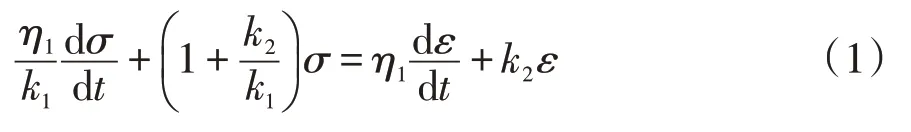
当σ≥σs时，

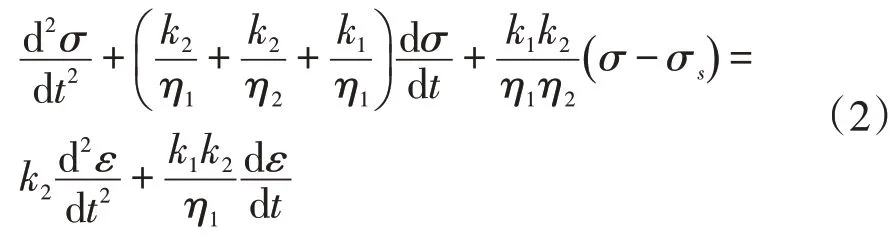
2）蠕变方程

当σ＜σs时，

当σ≥σs时，

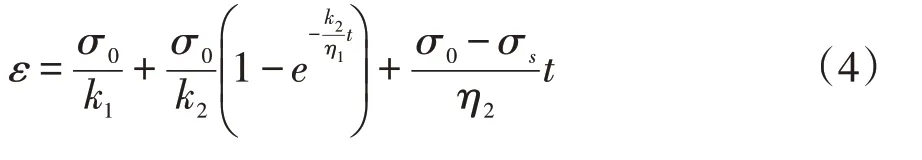
西原体模型可反映出当应力水平较低时，开始模型变形较快，一段时间后逐渐趋于稳定，发生稳定蠕变；当应力水平达到或超过材料某一临界应力值后，渐渐转化为不稳定蠕变。因此，该模型在岩石流变特性研究应用中使用广泛，特别在软岩流变特性的描述中适用。传统西原体模型的元件为理想的线性元件，只反映出蠕变的前两个阶段，不易完整描述岩石的其他流变特性。因此，为更全面地描述岩石的流变过程，在传统西原体模型的基础上，引入能够表征岩石材料变形停止、应力随时间增长而下降的参数[3]。为便于说明问题，以盐膏岩地层中油气井井筒应力变化为例进行研究。

1.2 改进后的流变模型本构关系

马克斯威尔体模型是由弹簧和阻尼器串联组合成的一种黏弹性体，该模型能对流变特征中的蠕变现象和松弛现象较好表达，符合钻井初期井壁岩石的流变规律。为此，结合前人对西原模型的改进，将马克斯威尔体与西原体模型结合起来，在模型的建立中串联阻尼器，建立改进的岩石流变西原体模型，如图2 所示。该模型阻尼器触发条件是当模型应变达到某一应变值εA时，岩石进入加速蠕变阶段对应的起始应变。

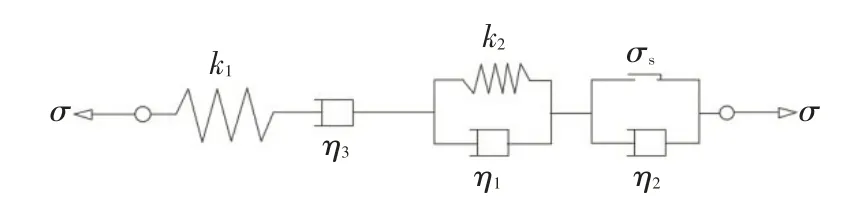
图2 改进的西原体模型

图2 中，σ为模型施加的总应力,MPa，σs为岩石的屈服应力，MPa；k为弹簧的弹性系数；η为黏性元件的牛顿黏性系数；ε为应变。依据文献[3]，得到改进后的模型在加速蠕变阶段的本构方程为[3]：

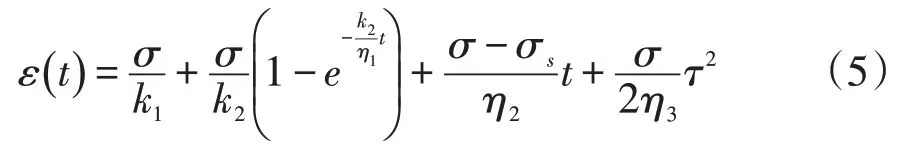
其中τ=t- |tε=εA,t｜ε=εA为岩石进入加速蠕变阶段的时刻。

当t=0 时，施加应力σ0，并保持σ=σ0不变，得到该过程下的蠕变方程为：

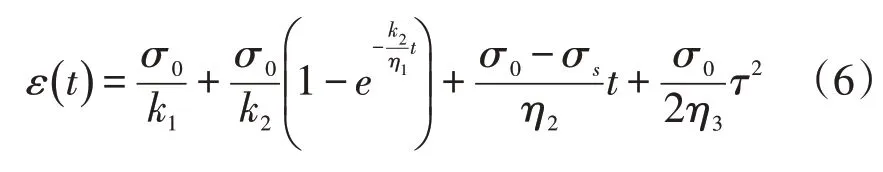
为了验证改进西原体模型分析岩石流变的准确性，假设应力大于摩擦片屈服应力（σ＞σs），取弹簧元件的弹性系数k1、k2为10 MPa，牛顿黏性体的黏性系数η1、η2为10 MPa·d ，η3为50 MPa·d ，σ0为10 MPa，模型屈服应力分别取90、80、70、60和50 MPa，得到不同屈服压力下改进西原体蠕变曲线，如图3 所示。从蠕变曲线变化趋势上看，岩石蠕变发生至第20 d时进入加速阶段，直至第26 d蠕变加速结束。整体看，改进后的西原体模型完成了从蠕变减速到等速，再到加速的全过程，证明改进模型对蠕变过程描述的适用性，可进行后续流变特性的探索[15]。

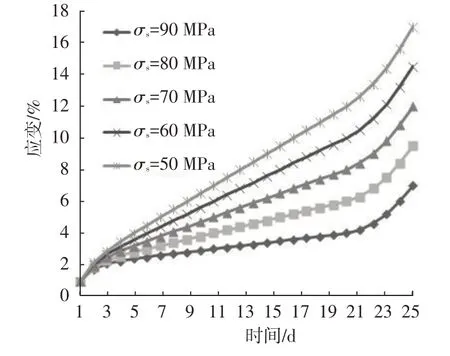
图3 改进后的西原体模型蠕变曲线示意图

1.3 改进后流变模型的松弛方程及其特征

当蠕变发生至一定程度时，岩石的变形将会保持在某一时刻的大小并且变化很小，此时认为应变ε为定值，此时，将模型的本构方程进行一阶微分后得到：

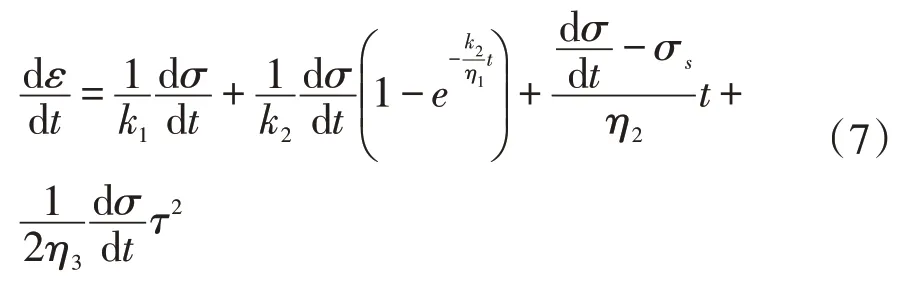
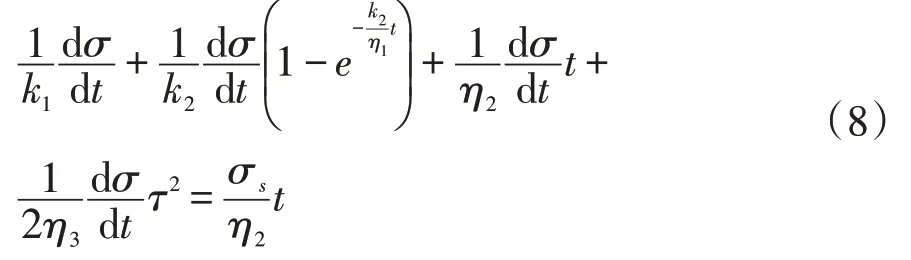
等式两边同时积分可得：

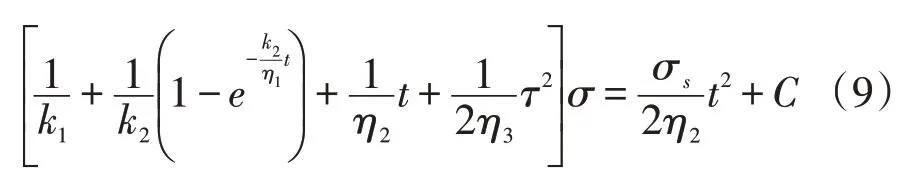
当t=0时，模型受到瞬时应力σ0，可得常数计算式：

得到的模型松弛方程表达为：

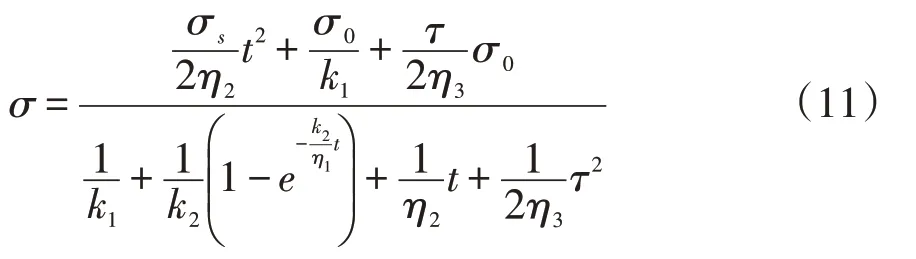
为了与岩石蠕变现象衔接，从蠕变过程结束后对松弛方程进行准确性验证，保持模型相同赋值条件，对方程进行模拟。模型分别赋予50、60、70、80和90 MPa 等屈服应力值[15]。模拟出的松弛结果如图4 所示，结合钻井初期井壁岩石后续流变特性发展，对蠕变发生后一段时间内的松弛方程进行模拟，从蠕变全过程结束起认为变形停止，从曲线中应力随时间的变化趋势上看，模型受到的应力从27 d 开始逐渐减小，符合松弛现象发生的应力变化情况，说明该过程为岩石松弛阶段。

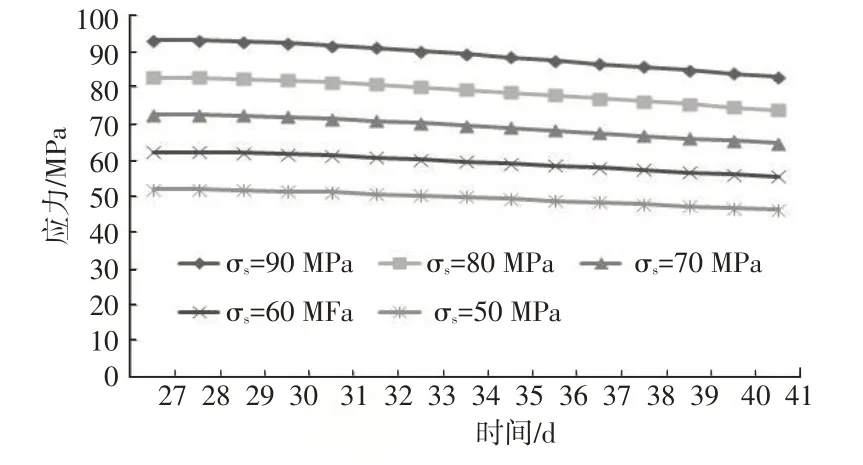
图4 改进后的西原体模型松弛模拟结果

结合改进模型后的松弛方程和模拟松弛曲线结果分析看，方程中的岩石应力值在发生蠕变之后开始减小，松弛曲线中的应力随时间的增长呈下降趋势。结合钻井初期井壁岩石的流变规律可以推断，当岩石的应变值达到松弛发生条件时刻对应的应变值时，此后岩石流变特征就进入了松弛阶段。在此之前，由图3 可知模型处于蠕变阶段的各个过程，在钻井初期的流变地层中，由于该段地层岩石在钻井后会发生应力变形，达到一定程度会贴合井壁，可以看成经历了从蠕变开始到蠕变结束的过程，即受岩层自身地应力下的应变逐渐减小直至停止的过程。可以判断流变地层岩石在蠕变之后产生松弛现象。为进一步验证推断，对松弛方程式（11）利用数学极限思想进行求解计算，过程如下。

随着时间的推移，当t→∞时，松弛方程为“型”极限函数，随即对方程进行求极限得：

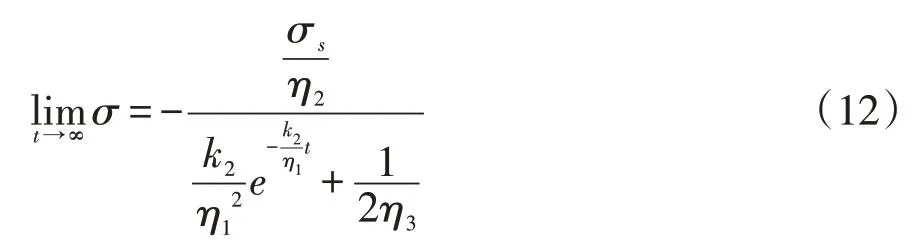
对于钻井初期的井壁岩石流变的工程问题，钻井导致的地层破坏，打破了流变地层原始地应力平衡，为平衡受力，应力则集中在井筒周围，该状态下的岩石就会发生蠕变现象。随着蠕变全过程结束，地层与井筒紧密贴合，岩石停止蠕变变形，接着表现出应力随时间的增长而减小的松弛现象，岩石流变特征会因实际工程条件的改变发生变化。

2 地应力计算及数值模拟

2.1 地应力计算验证松弛方程

利用松弛方程进行应力计算时，存在黏性系数和弹性系数等5 个未知量，必须确定松弛方程中涉及到的这些系数。通常以实验的方式对岩石流变本构关系中的方程进行参数识别，现有文献对该方面的实验研究较多，为方便计算，选用最贴近钻井初期岩石流变特性的蠕变数据对松弛方程进行参数识别，取长山岩的蠕变数据作为计算条件，改进后得到的蠕变方程存在5 个参数[15]，相应取5 组数据，其中100、200、300、350 和400 h 时的应变值分别为0.051、0.054、0.058、0.063 和0.067 mm，初始应力为14.72 MPa，屈服应力为11.34 MPa，代入公式（11）可得到弹性系数和黏滞系数值分别为：

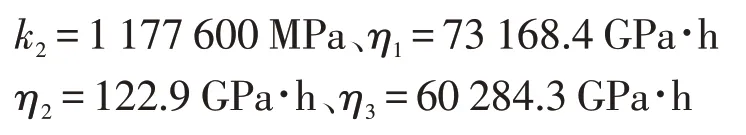
得到含具体参数的松弛方程：

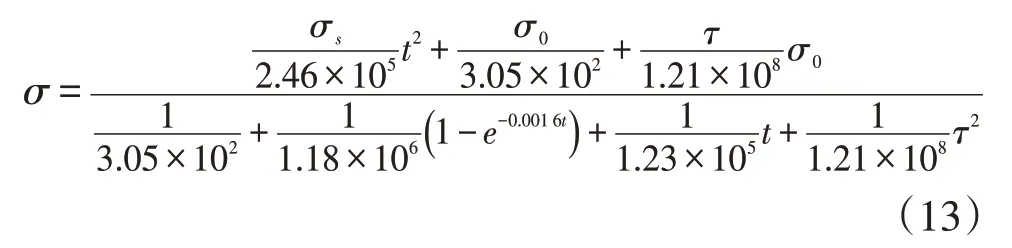
为了论证松弛方程结论的准确性，以某油田井区盐膏岩地层中岩石力学参数为例，结合地应力理论公式和有限差分数值模拟两种方法进行该地层地应力计算，结果与推导的流变松弛方程结果对比并分析误差。根据某油田实际地质数据和测井资料可知，该井区东西埋深在3 522～4 468 m，南北埋深在3 768～4 428 m 的盐膏岩蠕变地层，符合岩石流变特性的地层最大厚度约220 m，最小厚度约142 m，大部分厚度平均在142～168 m，符合条件的岩层包括泥岩夹层和泥膏岩夹层。该段地层岩石平均密度为2.186 g/cm3，屈服强度测算为65.4 MPa。其具体岩石力学参数见表1。

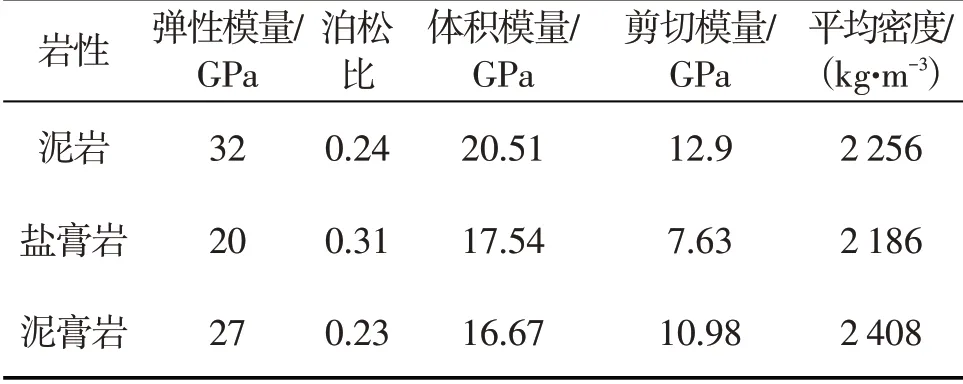
表1 某油田地层岩石力学参数

根据上覆岩层压力计算公式计算地层初始地应力，可得所取地层垂直地应力为112.05 MPa。结合我国地理条件现状，根据平均水平应力计算公式得116.4 MPa，水平主应力系数比值取0.7[1]，得到的水平最大主应力和水平最小主应力分别为136.94、95.86 MPa。

结合该地层岩石力学参数及理论计算的地应力结果，对含参数的松弛方程公式（13）进行赋值计算地应力。取屈服强度65.4 MPa，初始应力116.4 MPa，得到应力随时间变化情况如图5 所示，在26 h左右时应力值与理论计算结果大小相对应，水平应力平均值随即呈现出下降趋势，直至30.9 h时，平均应力值逐渐稳定在113.08 MPa，与地应力理论计算结果对比，平均误差为3.83%。

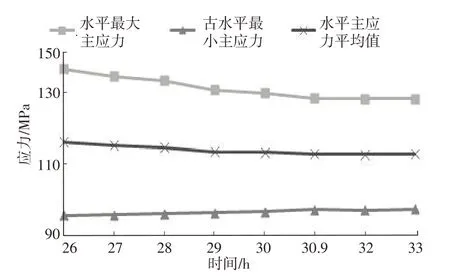
图5 松弛方程应力随时间的变化趋势

2.2 数值模拟验证松弛方程

为了多角度验证流变松弛方程的准确性和可行性，再进行数值模拟计算。FLAC3D 有限差分软件在大边界模型下的数值计算较其他数值模拟软件精度更高，计算更为准确，故选用该软件对上述井区流变地层简化进行建模计算。设定模型在水平方向上长度均为100 m，依据表1 中岩石力学参数，厚度方向自上而下按照20 m 泥岩层，30 m 盐膏岩层、30 m 泥膏岩层进行划分，模型总厚度为80 m。对整体模型统一划分网格，单元格个数为1 000，共1 000个正方体网格单元。

选用软件自带流变模型中的cwipp盐岩变形模型代替盐膏岩层，弹性模量取20 GPa，泊松比取0.31，体积模量取17.54 GPa，剪切模量取7.63 GPa，地层中的重力加速度9.8 m/s2，与表1保持一致。设置模型上表面压力为112.05 MPa，水平最大主应力为136.94 MPa，水平最小主应力为95.86 MPa。采用深埋工程初始地应力场的S-B 法计算生成，得到X方向上的水平应力云图，如图6所示[15]。

图6的计算结果显示，模型的x方向水平应力最大值为144.38 MPa；模型的y 方向水平应力最大值为99.62 MPa。利用FLAC3D 有限差分数值模拟结果对流变本构关系的计算结果进行校验，水平方向应力平均误差为7.25%。整体误差较小，验证了岩石流变本构松弛的准确性，可以用来计算流变地层的应力值。

图6 初始地应力场x方向应力云图

3 结论

1）改进的西原体模型适用于流变地层中的岩石变化规律。

2）在岩石发生蠕变之后，推导出的松弛方程体现出应力值随着时间的增长而下降，说明岩石进入松弛阶段。

3）将流变地层物理特征代入松弛方程进行计算，与地应力计算结果相比误差为3.83%；与FLAC3D有限差分软件数值模拟计算结果相比，平均误差为7.25%，推导的松弛方程可计算流变地层的应力值。