基于线结构光的型钢自动焊接位置检测技术
刘洪伟, 马立东, 马自勇, 张富泉, 杭嘉濠
(1.太原科技大学, 太原030024;2.太原重型机械装备协同创新中心,太原 030024;3.海安太原科大高端装备及轨道交通技术研发中心,江苏 海安 226600)
0 前言
H型钢是一种具有较高抗弯、抗扭、抗压等力学性能的钢材,因其重量轻、性能好、规格多、断面经济合理、使用方便和节省金属等特点,它在世界各国中正在逐步替代工字钢,占比也愈来愈大。研究发现,在不改变壁厚的条件下,适当的使用钢结构加强筋可以很大程度上增强钢结构建筑的强度和刚性,节约材料用量,减轻重量,降低成本。因此在H型钢上焊接加强筋不失为一种可行的方法。但在型钢加强筋的焊接过程中,型钢截面尺寸的测量是其焊接工艺的一个重要步骤,其检测精度关系着整个H型钢的焊接质量最终影响H型钢的强度与刚度。对于型钢的测量与检测,目前大部分都是接触式测量。接触式测量具有抗干扰能力强,检测精度高等优点但检测仪器精密且操作复杂,人工操作随意性大,而且接触式测量使用的工具会产生不可避免的磨损,对测量精度造成严重影响。非接触式测量排除接触式测量对柔性物体测量的人为等受力干扰,可以测量一些不可接触的物体,如辐射体、高温物体等。显然,非接触式测量相对于接触式测量,非接触式测量方式更符合发展趋势。作为非接触式测量方法中的典型方法,线结构测量技术是目前工业上最实用的非接触三维测量技术之一,具有原理简单、高精度、光条图像易于提取、易于实现、测试过程自动化等特点。因此,研究工业现场中的H型钢截面非接触式测量方法,对于型钢的准确焊接有着重要的意义和实际应用价值。
针对型钢的测量,刘燕[1]研究了一套H型钢截面尺寸结构光测量系统,采用九点标定法,标定方法简单,测量精度高,但图像处理算法较复杂,时间花费较多,实时性较差。刘庆纲等人[2]采用结构光的测量方法实现H型钢精密视觉检测,具有较高的测量精度,建立的测量系统满足大景深的测量需要,且具有较好的测量重复性和稳定性,满足测量需要。但所用标定方法忽略畸变的影响,标定的准确性需通过提高相机分辨率来保证。陈龙[3]采用激光位移传感器为测距元件,由计算机控制步进电机转动及发出数据采集命令。通过传感器和试件的相对运动对试件表面进行自动连续的扫描测量,测量数据经相关处理分析后导入软件,绘制出被测试件的三维图形,测量速度快且性能稳定但需要高精度的直线导轨。王肃伟[4]所研究的H型钢在线检测系统设计,有良好的设计方案,但是未进行试验验证,所以无法确定其性能。刘亚姣[5]提出一种基于可变形卷积与多尺度-密集金字塔的型钢表面缺陷检测算法Steel-YOLOv3,将深度学习思想应用到型钢表面缺陷检测中,检测精度与已有方法相比提高一些,满足实时性要求。于龙龙等人[6]基于平面靶标方法,提取照射在平面靶标的直线,提取多组直线通过最小二乘法拟合出激光平面,结合基于二维平面靶标标定完成整个系统的标定,计算简单,精度有了很大提高。但最终只得出一些标准量块的尺寸误差,对坐标误差这方面没有提及。王迪[7]提出了一种基于双目线结构光的传感器测量模型,并巧妙地采用柱形纸筒作为标定靶,简化结构光参数的标定流程,最终恢复物体的三维点云数据。段发阶等人[8]提出齿形靶标法,采用齿形靶标与一维运动相结合完成标定,但要求齿形靶标精度高。Liu等人[9-10]分别提出对球形目标的摄像机标定技术和线结构光标定技术,同样也是利用高精度靶标进行标定,简化了靶标点提取方式,提高了检测精度但靶标加工要求较高。张瑞峰等人[11]研究了一种新的线结构光标定方法:利用平面靶标上的点与相机光心所构成的关系,选取多组点求解2条及以上的光条中心点在相机坐标系下的坐标并基于最小二乘法,利用所有光条中心特征点计算光平面在相机坐标系下的方程。鉴于前人所研究的H型钢检测大都对尺寸精度行分析而对坐标精度研究较少,采用基于线结构光的H型钢测量系统与焊接机器人相结合的方法来评价坐标精度并对深度方向坐标存在误差问题提出一种误差补偿方法,减小坐标误差。
文中主要分为3个部分:系统的标定、图像处理和试验验证。第1部分为系统的标定,这部分又分为2个部分:①相机标定,主要求出相机内参和畸变参数,用于后续的计算与畸变矫正;②激光面与相机位置的标定,主要确定激光上的点相对于相机的位置关系,最终根据设立的世界坐标系及转换关系求得三维坐标并利用ABB机器人来验证准确性。第2部分为图像处理部分,给出关键点数据,用于计算最终结果。第3部分为试验验证,验证模型检测的数据和实际测得的数据的近似程度。
1 H型钢视觉标定原理
针对摄像机的标定方法已经非常成熟,例如基于径向约束的方法[12]、基于主动视觉的方法[13]、基于二维平面靶标的方法[14]等,基于数值拟合的线结构光视觉传感器的标定方法[15]。尽管那么多人提出标定方法,而关于结构光面的现场标定方法仍在不断研究之中。
1.1 相机成像原理
空间三维坐标到图像像素坐标的线性变换关系可由以下步骤实现。
设某一点的世界坐标为(xw,yw,zw),它在相机坐标系下的坐标为(xc,yc,zc),在图像物理坐标系下的坐标为(x,y),在像素坐标系下的坐标为(u,v)。世界坐标系到摄像机坐标系变化:
[xcyczc1]=[RT0T1]·[xwywzw1]=M2·[xwywzw1]
(1)
式中:R为3×3单位正交矩阵;T为平移矩阵;R矩阵和T矩阵是世界坐标系向相机坐标系变换的旋转矩阵和平移矩阵。以下为摄像机坐标系到图像物理坐标系变换。
由经典的成像原理知:
{x=f·xc/zcy=f·yc/zc
(2)
用归一化坐标(x′,y′)表示为:
{x′=xc/zcy′=yc/zc
(3)
归一化坐标与图像像素坐标的变换为:
[uv1]=[>fx0u00fyv0001]·[x′y′1]
(4)
由式(3)和式(4)联立得出像素坐标与相机坐标的关系:
zc·[uv1]=[>fx0u00fyv0001]·[xcyczc]
(5)
式中:fx,fy分别为u轴、v轴的有效焦距,且fx=f/dx,fy=f/dy;dx,dy分别为每个像素在x轴、y轴方向的物理尺寸;(u0,v0)为相机光轴与成像面的交点的像素坐标。进一步推导可得某一点的相机坐标之间的关系为:
{>xc=(u-u0)·zcfxyc=(v-v0)·zcfy
(6)
式中:u,v可以通过图像处理提取到;u0,v0,fx,fy可由相机标定得到,如果知道zc那么一个点的相机坐标都可求得。最终由式(1)、式(5)可得空间点与图像像素坐标点的对应关系:
zc·[uv1]=[fx0u00fyv0001]·[RT]·[xwywzw1]=M1·M2·[xwywzw1]
(7)
式中:M1为系统的内参数;M2为系统的外参数;对于固定测量系统,摄像机的内参数为常数。该模型为理想上的相机成像模型,用于工程上还是有一定的误差和不足,在实际生产中相机成像不可能完全满足中心投影关系,相机的中心线难免会产生弯曲现象出现光学畸变。除此之外,摄像机还可能由于成像过程的复杂性、图像分辨率低等因素造成成像点与空间点之间的非线性关系。所以考虑到相机具有径向畸变和切向畸变,切向畸变几乎没有,文中没有考虑切向畸变的影响,只考虑径向畸变的影响。由张正友标定法知:
{u′=u+(u-u0)[k1(x2+y2)+k2(x2+y2)]v′=v+(v-v0)[k1(x2+y2)+k2(x2+y2)]
(8)
式中:(u′,v′)为经畸变矫正后的像素坐标;(u,v)为未经畸变矫正的像素坐标。x与y为未考虑畸变情况下的归一化坐标,k1,k2为2个径向畸变系数。将式(8)代入理想的未考虑相机畸变的模型中,即代入式(5),可得
zc·[u′v′1]=[>fx0u00fyv0001]·[xcyczc]
(9)
1.2 线结构光测量原理
文中采用平面靶标进行相机的标定和激光平面的标定。单相机标定采用张正友标定法标定,技术已经很成熟,这里不再一一赘述。激光平面标定的目的是为了拿到激光平面与相机的位置关系,通过结合求得的内参得到激光平面在相机坐标系下的平面方程。
激光线照射在平面靶标,如图1所示。图1中所用棋盘格规格为23×22,一个方格是15 mm。
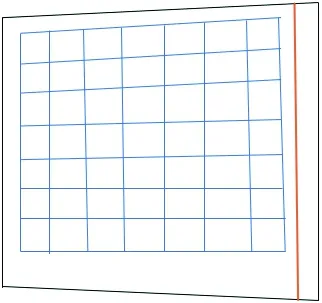
图1 激光条纹位置
通过拟合激光线提取激光线的直线像素坐标方程为:
a·u+b·v+c=0
(10)
式中:a,b,c为激光线上的像素点在像素坐标系下的直线方程系数。根据像素坐标与图像坐标的转换关系可以将得到的直线像素坐标方程转化为直线的图像坐标方程:
A·x+B·y+C=0
(11)
式中:A,B,C为激光线上的像素点在图像坐标系下的直线方程系数。根据像素坐标与图像坐标的转换关系可知:
(A,B,C)=(a,b,c)·[>1dx0u001dyv0001]
(12)
由这条激光线与相机光心所组成的平面方程为:
A·f·xc+B·f·yc+C·zc=0
(13)
将世界坐标系建在棋盘格上,即棋盘格平面在zw=0的平面上(在世界坐标系下),由此可以得出棋盘格平面在相机坐标系下的方程如下:
(0010)·[RT0T1]·[xcyczc1]=0
(14)
式中:R为相机坐标系与世界坐标系之间的旋转矩阵;T为相机坐标系与世界坐标系平移向量。联立式(13)与式(14) 可得激光中心线在相机坐标系下的坐标方程为:
{A1·xc+B1·yc+C1·zc+Dl=0A·f·xc+B·f·yc+C·zc=0
(15)
式中:A1,B1,C1,D1为棋盘靶标平面在相机坐标系下的平面方程的各个系数。多次转动棋盘格并使激光条纹射在棋盘靶标空白处,采用相同方法求得激光线上各点相应相机坐标,最后通过最小二乘拟合方法将这些点拟合成一个激光面,由此求得激光平面在相机坐标系下的平面方程为:
Ac·xc+Bc·yc+Cc·zc+Dc=0
(16)
式中:Ac,Bc,Cc,Dc为激光平面在在相机坐标系下的平面方程的各个系数。至此,可以得到激光平面相对于相机的位置关系,激光平面标定完成。最终与单相机标定得到的方程联立,即与式(9)联立实现整个系统的标定:
{f1(u,zc)=xcf2(v,zc)=ycAc·xc+Bc·yc+Cc·zc+Dc=0
(17)
式中:f1与f2分别代表u,v与xc,yc的关系3个方程,有xc,yc,zc3个未知量,其他参数和关系通过相机标定和激光平面标定获得。
2 H型钢视觉标定图像处理
文中基于MFC编写图像显示与处理界面程序,图像处理方面基于OpenCV库。除上面提到的标定方法比较核心,另外一个核心的就是图像处理的算法。文中搭建试验台如图2所示。

图2 试验台
线结构光增强特征,将复杂的三维轮廓转化为二维图像,因为激光线碰到不同的三维物体表面会被调制形成变形条,呈现在图像中的是不一样的折线,通过识别二维图像中折线的关键点,利用标定方法转化为机器人坐标系下的三维坐标从而实现三维轮廓的。考虑到所获取图像中的激光线是有宽度的,它不是单像素的,拟对激光线进行细化,细化成以单像素为单位的轮廓线,以便接下来的关键点提取。
2.1 提取激光线条纹中心
如何精准、完整地提取投射到物体表面的线结构光是结构光视觉测量的关键问题,而结构光的中心线提取是不得不面临的问题。可将当前所发展的线结构光中心线提取模型大致分为2类:采用传统算法的提取模型和基于深度学习算法的提取模型。简单地说前者算法简单,后者适应复杂环境,算法复杂。Nguyen等人[16]提出了利用高斯峰值评判激光条纹中心线像素位置,简单高效。鉴于型钢的形状轮廓较为单一,选用传统算法的提取模型。
文中提取激光线的过程大体如下:对激光线图像进行高斯滤波,并采用大津阈值法进行阈值分割,之后提取轮廓并画出轮廓,将这些轮廓点都存到容量里去,基于几何中心提取法,取轮廓点对的中心作为激光条纹中心,并在图像中用相应颜色线画出来,在通过几个关键点的像素或位置关系准确求得它们的图像坐标,并将需要的几个点坐标存写入文件,为接下来坐标转换做准备。处理的图片如下所示:图3为提取到的激光线轮廓图,图4为找到的几个关键点位置显示图,图5为关键点位置示意图。

图3 提取的轮廓图
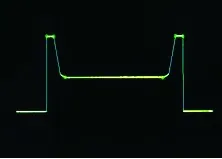
图4 关键点图

图5 点示意图
2.2 拟合激光直线
对于关键点的检测,思路是通过拟合细化之后的激光直线并根据拟合的直线与原图像的交点作为关键点,作为2.1章节的检验与补充,比较两者的找到的点的位置,对图像处理结果的准确性作判断。
图6为拟合的激光线的直线,蓝色线表示拟合的线,红色为未经处理的激光线。通过图5中4个示意点的位置及图6中右边直线的位置,可对焊接轨迹进行规划,即知道焊缝的位置,联合焊接机器人完成焊接任务。根据相应关键点像素位置找到的几个点坐标见表1。
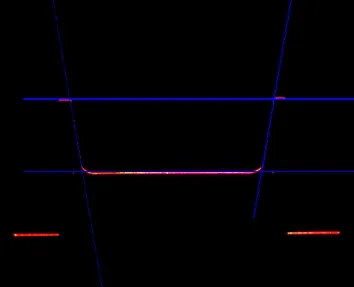
图6 拟合的直线
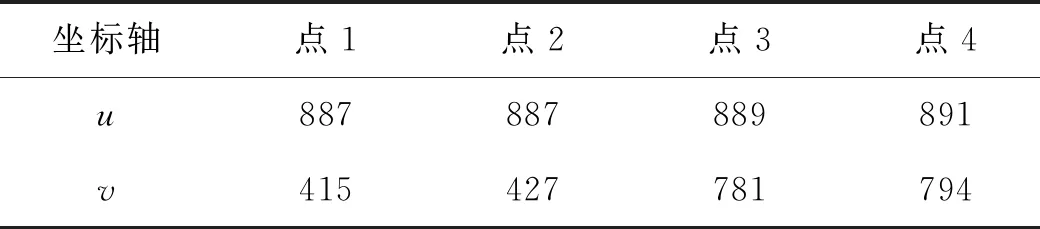
表1 关键点的图像坐标
3 试验与结果分析
3.1 线结构光标定试验
为更好提取激光线,应确保激光线不与棋盘格上角点所在直线相交叉,激光条纹位置最好是在平面靶标的空白部分,试验过程大体如下:①将标定板调整任意位置,注意要让激光线照射在棋盘平面空白部分并采集每个位置的照片,必须视野中的棋盘格完整无缺;②按步骤一采集10~20组照片,文中采集了18组照片,控制相机进行拍照,图7和图8为2个不同位置采集的照片;③根据前文线结构光测量原理部分求得这18组激光线在相机坐标系下的直线方程;④18组直线方程根据最小二乘法原则拟合出一个激光光平面得到的平面方程为:

图7 状态A下的标定板

图8 状态B下的标定板
2.302xc-0.014 03yc-zc+1 219=0
(18)
图9为用Matlab拟合得到的激光平面,RMSE为16.296 5。可以看出通过多组激光线上的点拟合的激光平面还是比较符合的。
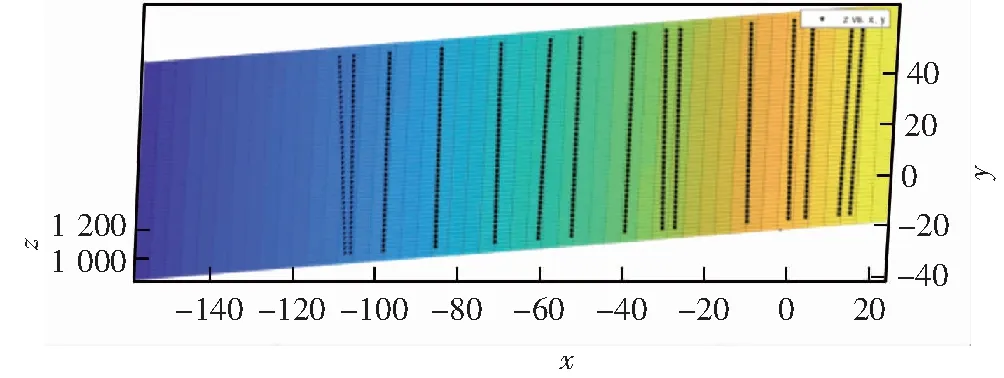
图9 拟合的激光平面
3.2 系统测量试验
搭建试验平台如下:相机采用大恒公司的Mer-231-41-GC-P相机,激光器采用FU650AB100-GB16线激光器,单相机标定采用张正友标定法,采用Matlab APP中的标定工具箱标定相机内外参数,用18组标定板求得其中内部参数见表2。

表2 摄像机内部参数标定结果
张氏标定法相对其他标定法来说操作简单,标定精度高,适合快速标定,满足一般精度的需求,针该系统的测量的任务,张氏标定法较为契合,故选用此法来标定单相机。将相机标定结果与要处理得到的图像像素坐标代入式得各个点的相机坐标,并最终转换成所设的一个世界坐标系下的世界坐标,转换关系如式(19)所示,这将用于机器人的运动指导。
[xwywzw]=[RT0T1]-1·[xcyczc]
(19)
设的世界坐标系如图10所示。其中,z坐标垂直于x轴与y轴构成的平面且符合右手坐标系垂直向外,通过相机标定得到外参及拟合的激光平面方程和提取的像素点最终得到所测关键点的世界坐标。

图10 世界坐标系
前面系统已经搭建好了,接下来就是测量。针对坐标转换后世界坐标深度方向存在偏差问题,提出一种误差多项式拟合方法,能有效减小坐标误差,实现准确点到点定位,为焊接机器人引导焊接提供可能。
方案步骤为:测量多种规格的标准量块,通过上文提到的测量系统算出每个量块的深度方向坐标z及测量结果与真值的偏差值dz,通过170组数据反映两者的函数关系,采用多项式拟合得到不同高度下被测物体的偏差值,将偏差值补偿到计算的被测点深度方向的坐标上。表3为拟合多项式的指标参数。

表3 指标参数
将此方法应用到型钢测量上,针对的是3种不同型号的型钢,检测的点选择了3种型号H型钢中1, 4示意点,结果见表4。
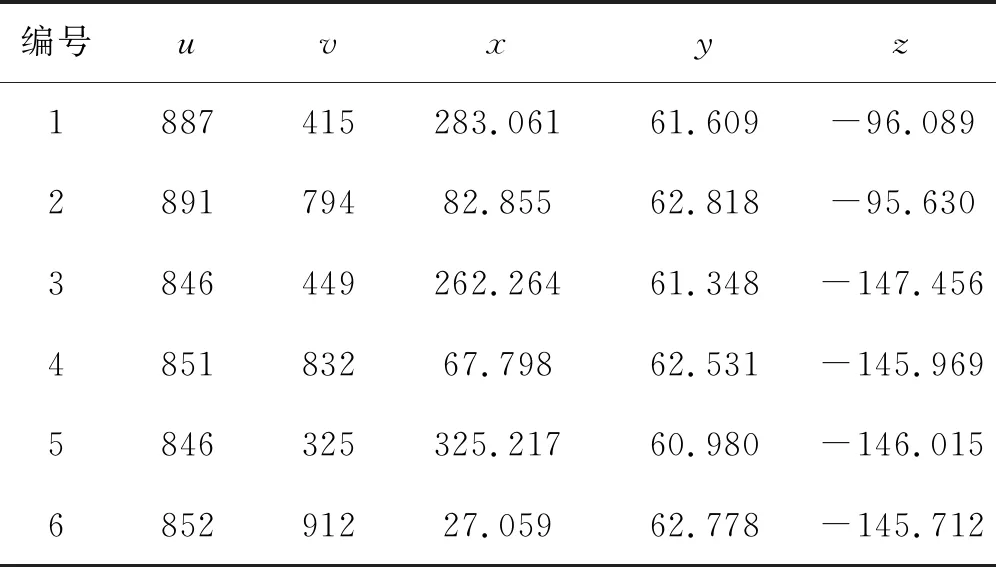
表4 测量结果
3.3 误差分析
在机器人示教器中设立工件坐标系为前言所说的世界坐标系,通过机器人来起到一个三维测量仪的作用,手动控制机器人到每一个激光关键点上,读取当时的工件坐标作为测量数据的依据,对比测量系统检测求得的世界坐标数据做误差分析。图11是表4中的测量值与机器人测量之间的坐标误差。由图11可知误差大致在3 mm以内,坐标误差是综合了x,y,z方向的坐标误差,其中y方向为主要误差,考虑到用机器人测坐标时探针在沿着激光线法线方向也就是y方向上难以精确定位到激光线中心位置,存在1~2 mm的偏差实属意料之内。显然如果不考虑y误差,坐标误差就显著减小,当然,这是人为因素造成的误差,可以避免,结果预计可以到1 mm以下。如果坐标误差降到 1 mm以下,对于指导机器人焊接是可能的。
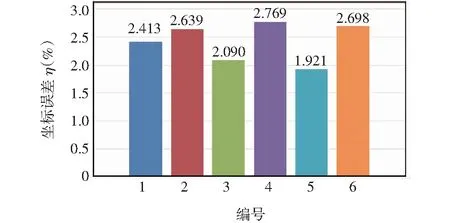
图11 坐标误差图
4 结论
(1)提出一种基于线结构光的型钢焊接位置检测方法与系统,该方法利用二维平面靶标与相机的相对位置关系及激光平面与相机的相对位置关系完成标定工作,提出了适用于H型钢的图像处理方法可以实时获得关键点的三维坐标,并且与机器人坐标系连接起来实现指导机器人进行下一步的焊接动作,实现简单操作性强,而且图像处理算法简单计算量小,适合实时处理。
(2)针对关键点坐标误差较大的问题,提出一种误差拟合方法,利用不同高度的标准量块拟合不同高度的误差曲线进而预测系统测量误差,实现误差补偿,将坐标误差降到1 mm以下,满足焊接使用要求。

