双绕组变压器集总等效电路频率响应的电路矩阵算法研究
王松,王薇,曾鑫海,杨丰野,张那明,段娜娜,王曙鸿
(1.西北农林科技大学动力与电气系,712100,陕西杨凌;2.西安交通大学电力设备电气绝缘国家重点实验室,710049,西安)
变压器作为电力系统中电能转换与传输的关键设备,确保其安全、可靠的运行状态对维护电网的稳定具有重要意义[1-3]。然而,随着我国电网容量以及负荷的增多,电网的短路电流水平也不断提高,导致因短路造成的变压器绕组故障也随之增加。国际大电网会议的变压器可靠性工作小组调查了1996—2010年世界范围的48个单位的900多起重大变压器事故,深入分析相关数据后发现:绕组发生故障所占比例最高[4-5]。国家电网公司研究了2005—2015年近10年在运的110(66) kV及以上电压等级的变压器的运行数据,发现变压器绕组发生故障的次数最多,占变压器总故障的35.7%[6]。因此,准确地确定变压器绕组的状态对预防和降低变压器故障风险有重要作用。
频率响应分析法(frequency response analysis method,FRA)作为一种有效的变压器绕组故障诊断方法,由于其对绕组变形的高灵敏度、检测的非破坏性以及测试数据的高重复性,使其成为变压器绕组变形检测领域应用最为广泛的方法之一[7]。FRA法主要依据故障前后绕组频率响应曲线的变化规律进行绕组的故障判定。因此,深入挖掘隐藏在绕组频率响应中能够表征绕组状态的特征信息成为了确定绕组故障状态的关键。然而,由于变压器自身封闭性、设备昂贵等特点,使得研究人员在开展变压器绕组故障类型、变形程度与变形位置与绕组频率响应内在联系研究时,很难直接对一台实际的变压器绕组设置相应的变形故障。为解决这一问题,变压器绕组的仿真研究方法被全世界研究人员广泛采用。快速准确地获得变压器绕组等效电路模型的频率响应成为顺利开展绕组仿真方法研究的关键。因此,研究并选择高效的电力变压器绕组等效电路频率响应计算方法,特别是针对拥有线饼数量多的电力变压器,具有非常重要的理论意义和工程价值。
变压器绕组等效电路模型主要可分为3类:多导体传输线模型、混合模型和集总参数等效电路模型。多导体传输线模型将绕组的每一条线匝看成一条传输线,基于单位长度的传输线等值参数,利用传输线理论建立的绕组模型。该模型在变压器绕组的过电压分析[8-9]和局部放电[10-11]研究中应用最为广泛。由于该模型以线匝为基本单元,导致较难通过修改模型相关参数模拟典型的绕组变形故障。因此,限制了多导体传输线模型在变压器绕组变形检测领域的应用。文献[12]建立了一个单绕组变压器的多导体传输线模型,利用COMSOL建立了该绕组的3D模型,通过修改绕组结构模拟故障并计算了不同故障下绕组电容和电感参数值,最终将参数带入到多导体传输线模型中。
混合模型是王赞基教授为分析变压器等电力设备内部特快速暂态响应以及线圈内局部电磁振荡而提出的[13]。该模型集合了变压器绕组分布参数和集总参数的特点,是介于多导体传输线模型和集总参数等效电路模型间的一种模型。国外学者Shintemirov等[14]将该模型应用到了绕组状态检测领域,建立了一个单绕组的混合模型并计算了该绕组模型的频率响应。文献[15]针对一台单绕组变压器,建立了该绕组的混合模型,仿真获得了变压器绕组的频响特性,通过改变相关参数仿真了轴向位移、径向位移和高接触电阻故障,并研究了这些故障下的频率响应曲线变化规律。然而,以上文献都仅针对单绕组变压器展开,并未考虑绕组二次侧绕组的影响。混合模型以线饼为基本单元,与多导体传输线模型相比,所建立方程的维数减小了,但该模型存在集总电路部分的元件参数不易确定的问题[13]。
集总参数等效电路模型是依据绕组的物理结构,以绕组的单线饼或双线饼为基本单元而建立的模型。该模型结构简单、参数计算容易,因此在变压器绕组仿真建模与频率响应分析中被广泛采用。文献[16]利用ANSYS/ANSOFT Simplorer软件搭建了绕组的集总参数等效电路,研究了绕组自由翘曲和强力翘曲故障下的频率响应曲线的变化特征。文献[17]以双线饼为基本单元,利用PSPICE软件对一个单绕组变压器进行了等效电路建模和频率响应计算。对于线饼数量较少的变压器,利用成熟的电路仿真软件具有较高的计算效率,但当线饼数增多时,相应的建模时间会明显增加。文献[18]基于状态空间法推导了二次绕组短接的双绕组变压器的频率响应函数,并依据该频响函数计算得到了绕组频率响应曲线以及频响函数的零极点。状态空间法需要选择相互独立的状态变量建立状态方程和相应的输出方程,所以该方法推导过程较为复杂。文献[19]提出了一种变压器绕组梯形网络频率响应的矩阵算法,该方法的实质就是节点电压方法,但将等效电路模型中支路分成阻抗和导纳支路,在节点电压列向量求解时,还需对相应的矩阵进行修改,导致推导过程过于繁琐,影响计算效率。同时,由于难以将PSPICE或者Simulink搭建电路所用时间与构建节点电压方程的时间作比较,所以仅对比了所述算法、PSPICE和Simulink这3种算法的方程求解时间。然而,本文研究发现,节点电压矩阵方程的求解时间仅占算法总耗时的5%左右。因此,算法其他部分的耗时情况也需要进一步对比分析。
针对以上问题,本文基于电路理论,定义了双绕组等效电路的广义支路,并据此构建绕组等效电路模型的支路电压、电流矩阵;通过选择节点、独立回路和独立割集,基于基尔霍夫电压和电流定律的关联矩阵形式、独立回路矩阵形式、独立割集矩阵形式,推导了等效电路频率响应的节点电压方程、独立回路电流方程与独立割集电压方程的矩阵算法;利用Multisim电路仿真软件对所提3种计算绕组等效电路FRA曲线的矩阵算法的正确性进行验证;对3种算法进行了矩阵求解时间、矩阵装配时间和总计算时间的对比。本文研究成果应可为工程技术人员选择相应的频率响应计算方法提供指导。
1 变压器绕组等效电路模型与广义支路
1.1 双绕组变压器集总参数等效电路模型
图1为一个双绕组变压器的集总参数等效电路模型。该模型以一个线饼为单元,每个单元包含了高压和低压纵向电容Csh、Csl,对地电容Cgh、Cgl,串联电感Lsh、Lsl,串联电阻Rsh、Rsl,高压与低压绕组之间的并联电容Chl,高压绕组线饼间的互感MHV(i,j),低压绕组线饼间的互感MLV(i,j),高、低压绕组各个线饼间的互感MHL(i,j)。该等效电路的末端电阻R0为匹配电阻。图1模型含有n个线饼,对应含有2(n+1)个节点(不考虑接地节点且接地节点作为参考点)和7n+5条支路。按照由低压到高压、同类支路连续标号的原则对每条支路进行编号。此原则可使列写的支路导纳或者阻抗矩阵中同类参数在一起,方便矩阵列写和编程。图1中各支路箭头的指向表示电流的方向。

图1 双绕组变压器的集总参数等效电路模型
1.2 广义支路的建立
建立变压器绕组等效电路方程矩阵算法时,需要建立支路方程,针对电感支路间的耦合互感,利用电流控制的电压源进行表征。复频域下等效电路第k条广义支路的定义见图2。根据支路电压、电流关系,可得
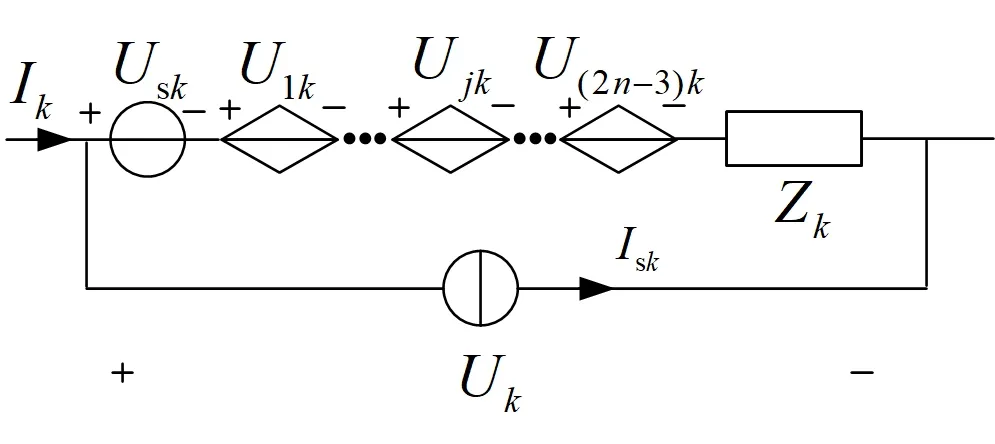
图2 广义支路
Uk(s)=Zk(s)Ik(s)-Zk(s)Isk(s)+Usk(s)+U1k(s)+…+Ujk(s)+…+U(2n-3)k(s)
(1)
式中U1k、Ujk与U2(n+3)k分别表示第1、j、2n-3条电感支路与第k条电感支路的互感电压,其中j≠k。U1k、Ujk与U2(n+3)k分别等于第1、j、2n-3条电感支路的支路电流乘以相应的互感值。
1.3 支路电压和支路电流的矩阵形式的建立
将广义支路推广到整个绕组等效电路7n+5条支路,可得
(2)
将式(2)写成矩阵形式
U=ZI-ZIs+Us
(3)
式中:U与I分别为支路电压与支路电流向量;Us与Is分别为支路电压源和电流源向量;Z为支路阻抗矩阵,根据图1中各支路的编号顺序列写,具体为
(4)
式中:ZLMR为高、低压绕组各串联电感支路的阻抗以及它们之间的互感阻抗矩阵;ZC为各电容支路的支路阻抗矩阵。ZLMR计算式为
(5)
(6)
(7)

(8)
ZC计算式为
(9)
(10)
由于绕组集总参数等效电路各支路不含电流源,式(3)可简化为
U=ZI+Us
(11)
由于Z为方阵且可逆,式(11)可转化为
I=YU-YUs
(12)
式中Y为支路导纳矩阵,且Y=Z-1。
2 节点电压方程矩阵算法
2.1 等效电路节点电压方程的矩阵形式
基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)的关联矩阵形式[20]分别为
(13)
式中:Un为节点电压向量;A为关联矩阵,维数为(2n+2)×(7n+5),该矩阵中的元素akj可依据等效电路各支路的编号顺序依次得到,公式[20]为
(14)
将式(13)代入式(12),即可得到节点电压方程的矩阵形式
AYATUn=AYUs
(15)
2.2 频率响应计算
变压器绕组等效电路的频率响应为输出电压与输入电压的比,利用直接分解法求解式(15)即可得到等效电路模型节点电压向量。由于输入电压Un(1,1)已知,因此提取节点电压向量Un的第2n+2个节点电压Un(2n+2,1),即可计算得到双绕组集总参数等效电路模型的频率响应,公式为
H=20lg[Un(2n+2,1)/Un(1,1)]
(16)
3 独立回路电流方程矩阵算法
一个平面网络的网孔数目就是独立回路的数目[21]。根据此原则,将图1的双绕组等效电路模型视为平面网络,取该网络的网孔作为等效电路模型的独立回路,设定回路的方向为顺时针方向,具体如图3所示。当绕组线饼数为n时,对应的独立回路的数目为5n+3。需要注意的是,由于高、低压绕组的对地电容都接地,两个接地点实质上是相连接的(如红色虚线所示)。因此,此处仍存在一个独立的网孔,根据独立回路可列写出独立的回路方程组。
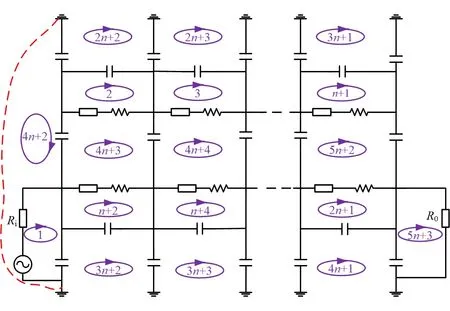
图3 绕组等效电路的独立回路
3.1 等效电路独立回路电流方程的矩阵形式
基尔霍夫电压定律和基尔霍夫电流定律的独立回路矩阵形式分别为[22]
(17)
式中:B为独立回路矩阵,维数为(5n+3)×(7n+5);由于所选回路为独立回路而非基本回路,维数为(5n+3)×1,因此Ih为回路电流向量。B矩阵中的元素bkj需按照支路和独立回路的编号顺序,公式[22]为
(18)
将式(18)代入式(11),即可得到独立回路电流方程的矩阵形式
BZBTIh=BUs
(19)
3.2 频率响应计算
求解式(19)可以得到等效电路的回路电流向量。等效电路末端匹配电阻所在回路为第5n+3回路,该回路电流等于匹配电阻所在的支路电流。因此,提取第5n+3个回路的回路电流并乘以匹配电阻值50 Ω即为第7n+5支路的支路电压,也等于该支路所在的第2n+2个节点电压。因此,计算得到输出端的节点电压Un(2n+2,1),公式为
Un(2n+2,1)=50Ih(5n+3,1)
(20)
然后,利用式(16)即可得到绕组等效电路的频率响应。
4 独立割集电压矩阵算法
根据图论可知,每一个图可取不同的割集,若选择的每个割集都仅含有一个树支时,该割集为基本割集。由于基本割集属于独立割集,因此由基本割集建立的割集电压方程彼此相互独立,方程有解且唯一。然而,选择基本割集时,需要先选择出树支与连支,然后选择相应的割集,并使得每个割集只切割一条树支。显然,对于结构复杂的图,利用基本割集的算法建立割集电压方程将会十分复杂和耗时。为了方便割集电压方程的列写,避免树支和连支的选择问题,本文选取绕组等效电路的独立割集,具体的割集选择如图4所示,图中箭头表示割集方向。可以看出,第一个割集切割了1号节点以及与其相连的支路,之后的割集较前一个割集都切割了一个新的节点以及该节点所连接的支路,这样就保证了每个割集的独立性。

图4 绕组等效电路的独立割集
为了证明所选割集为独立割集,可依据图1各支路的编号顺序以及图4中各个割集所包含的支路,对每个割集列写KCL方程,可得
(21)
将式(21)写成矩阵形式
CI=0
(22)
计算系数矩阵C的秩为2n+2,其等于该矩阵的行数,证明系数矩阵C各向量线性无关,因此表明所选割集是独立割集。此时,式(22)也称为基尔霍夫电流定律的独立割集形式,C为独立割集矩阵,该矩阵中的元素ckj也可按照支路和独立割集的编号顺序得到,公式[23]为
(23)
4.1 等效电路独立割集电压方程的矩阵形式
基尔霍夫电压定律的独立割集矩阵形式为
CTUg=U
(24)
式中Ug为割集电压,表示的是被割集分割的电路的两部分间的虚拟电压[24]。
将式(22)、(24)代入式(12),即可得到独立割集电压方程的矩阵形式
CYCTUg=CYUs
(25)
4.2 频率响应计算
求解式(25)可以得到电路模型中的独立割集电压向量Ug。然而,又因为每条支路的电压等于切割该支路的全部割集电压的代数和[24],而图4中末端匹配电阻所在支路仅被最后一个割集(第2n+2个)切割,因此直接取Ug(2n+2,1)即为末端匹配电阻支路的电压。将该电压代入式(16)即可得到绕组等效电路模型的频率响应。
5 基于Multisim的频率响应仿真验证
本节利用电路仿真软件Multisim和提出的绕组等效电路频率响应的矩阵算法分别对两组不同参数的案例进行FRA曲线计算,通过对比验证所提算法的正确性。
案例1与案例2分别是一个含有7饼与一个含有5饼的双绕组集总参数等效电路模型,两个案例的等效电路模型参数见本文首页OSID码中的开放科学与数据,计算得到的FRA曲线分别如图5和图6所示。可以看出,针对两种不同案例参数,3种算法计算得到的FRA曲线彼此基本完全重合,并与Multisim得到的FRA曲线重合度非常好,仅在个别峰值点处有一点差异。该差异主要是由于自编程中的互感元件是直接赋值的,而Multisim软件中的互感是通过输入互感系数赋值的,因此就需要利用自感和互感值求解互感系数,而计算过程中的有效值位数差异就带来了曲线的微小偏差。

图5 案例1的FRA曲线对比

图6 案例2的FRA曲线对比
从两个案例的FRA曲线对比结果可知,本文所提算法能够准确计算双绕组集总参数等效电路模型的频率响应,并且所提算法对不同的案例参数具有适用性。
6 电路矩阵算法对比分析
3种电路方程矩阵算法的流程图如图7所示。

图7 电路方程矩阵算法流程图
通过对比3种算法的计算流程不难发现,在完成等效电路模型各支路、回路和节点的编号后,主要的计算步骤可以分为3步,分别为:建立广义支路矩阵的电压、电流矩阵形式,列写电路方程矩阵,求解电路方程矩阵。需要说明的是,由于选取独立节点、独立回路和独立割集的时间难以进行量化,因此本文仅从电路方程矩阵的装配时间、方程求解时间以及总计算时间这3个方面对比。
电路方程矩阵的装配时间包含了在对节点与支路编号、独立节点、独立回路和独立割集选择完成的基础上,根据它们之间的编号和关系列写关联矩阵A、回路矩阵B以及割集矩阵C的时间,根据各种编号顺序建立广义支路电压、电流矩阵的时间(列写支路阻抗矩阵或者支路导纳矩阵的时间),以及构建完成电路方程各系数矩阵的时间,该时间主要是由线饼数量决定的,绕组线饼数量越多,各矩阵的维数越大,相应的矩阵的列写时间、矩阵求逆时间以及矩阵相乘的时间就会越长,装配时间就会越长。除此之外,仿真软件的不同、编程方法的不同以及电脑性能的差异都会对结果产生一定的影响。为了避免仿真软件与电脑性能差异对计算时间的影响,本文所提算法是在MATLAB 2015b中编程实现的,计算机的基本配置为Intel(R) Core(TM) i7-8750H CPU和8 GB RAM。与此同时,本文对3种算法均采用相一致的编程逻辑和基本语句以尽量避免编程方法的不同对计算时间的影响。方程求解时间指求解电路方程矩阵,计算电路末端匹配电阻处节点电压、回路电流和割集电压的时间。总计算时间指矩阵装配时间与方程求解时间之和。
针对案例1与案例2中两组不同的等效电路元件参数值,考虑绕组线饼数较多的场合,如线饼数N分别为100和200,分别获取3种矩阵算法的计算时间,结果如表1与表2所示。需要说明的是,表中的时间为所有扫频点的计算时间总和,频率响应的扫频范围为1 kHz~2 MHz,共有3 302个频率点。

表1 案例1中算法计算时间对比

表2 案例2中算法计算时间对比
观察表1与表2中可知,两种案例参数下,独立回路电流矩阵算法的总计算时间和方程求解时间都是最长的,较节点电压和割集电压矩阵算法增加了一倍多的时长。这主要是因为独立回路的数目较大,由其构成的方程的系数矩阵维数为(5n+3)×(5n+3),远远大于其他两种方程的系数矩阵维数,方程系数矩阵的维数如表3所示。这使得方程求解时间和方程矩阵的装配时间增加,导致总的计算时间变长。与此同时,案例1中独立回路电流矩阵方程的求解时间占总时间的20.14%和21.87%,案例2中独立回路电流矩阵方程的求解时间占总时间的20.69%和21.98%,而两个案例中节点电压和独立割集电压矩阵方程的求解时间大约都为总计算时间的5%左右。因此,整体而言,矩阵装配时间才是3种算法最为耗时部分。

表3 方程系数矩阵的维数
在线饼数为100与200情况下,独立割集电压与节点电压矩阵算法的方程求解时间非常接近。在总计算时间方面,独立割集电压矩阵算法较节点电压法更少,但相差不大。当线饼数为200时,两个案例中的这两种算法计算时间都仅相差8 s左右。通过深入分析发现,该时间差异主要是由于列写导纳矩阵Y以及相应的关联矩阵A与独立割集矩阵C引起的。
通过对比表1与表2的数据可知,对于参数不同的两个案例,3种算法的各种计算时间相差不大,同类型的计算时间非常接近,表明元件参数的变化对算法的计算时间有影响,但影响程度非常小,基本可以忽略。
7 结 论
本文对用于计算双绕组变压器集总参数等效电路频率响应的电路方程矩阵算法展开研究。通过建立广义支路,避免了将各支路划分为导纳与阻抗两类支路。在建立方程过程中,利用基尔霍夫电压、电流的不同矩阵形式,结合广义支路电压、电流矩阵,便捷地得到了绕组等效电路频率响应的节点电压、独立回路电流、独立割集电压电路矩阵算法,在整个推导过程中,不必对任何一个矩阵进行改造,降低了推导难度,提高了频率响应计算效率。3种算法与成熟电路仿真软件计算结果相一致,验证了所提算法的正确性。
本文提出的双绕组变压器集总参数等效电路模型的独立割集选取方法,避免了利用基本割集时需对等效电路图选择树支和连支的复杂过程,简化了割集电压矩阵算法的应用难度,有助于割集电压矩阵算法在变压器绕组等效电路中频率响应分析、阻抗特性分析等领域的应用。
分析3种算法的建立过程,并对3种算法的方程求解时间、矩阵装配时间以及总计算时间进行对比,结果发现:对于含有线饼数目较大的双绕组变压器,独立回路算法计算时间最长,节点电压矩阵算法次之,而按照本文提出的独立割集选择方法所推导的独立割集电压矩阵算法的计算时间最少。因此,在对计算时间成本要求较为苛刻的场合,可优先选择该算法。然而,由于双绕组等效电路中节点的选择要比独立割集的选择简单,而两种算法的计算时间差异又较小,因此考虑前期的准备时间,节点电压矩阵算法仍是最佳的选择。

