液氧涡轮泵新型螺旋阻尼密封泄漏特性研究
动密封被广泛应用于叶轮机械中,以减小泄漏、提高效率和转子的动力稳定性。在液氧涡轮泵中,动密封在高压、低温推进剂下的工作条件
更为苛刻。由于离心轮凸肩密封在涡轮泵中承受最大的压降和旋流速度,液氧涡轮泵的主要工质泄漏来自于离心轮前后的凸肩间隙。采用先进的动密封技术有效地控制离心轮凸肩密封的泄漏量和流体激振力,对涡轮泵的运行效率、轴系稳定和深度变推力具有重要作用
。
农业科研单位作为财政对农业科研投入的重要载体,研究农业科研项目绩效评价具有十分重要意义。通常绩效评价的主体包括财政部门、科研主管部门和项目实施单位。其中项目实施单位是基层的评价主体,也是直接负责农业科研项目的实施单位,对于农业科研项目的绩效评价起到重要作用,因此笔者侧重从项目实施单位角度,探讨农业科研项目绩效评价问题。
目前火箭涡轮泵中常用的动密封技术包括迷宫密封、唇式密封、浮环密封和机械密封等密封形式及它们的组合。迷宫密封由于结构简单、成本低、对热和压差变化具有较大容差等优点,在火箭涡轮泵中应用最为广泛。然而,实验和数值研究表明:迷宫密封在有效控制泄漏流动的同时,会在转子表面产生显著的流体激振力,易诱发转子系统失稳
。随着火箭涡轮泵向高压力、高转速、深度变推力方向发展,迷宫密封介质压力、密度逐渐增大,密封间隙逐渐减小,密封流体激振力已成为涡轮泵超临界柔性转子涡动失稳的重要激励源。
采用阻尼密封代替传统迷宫密封,可增大轴系阻尼、改善转子的稳定性,目前典型的阻尼密封结构包括孔型阻尼密封、蜂窝阻尼密封和袋型阻尼密封。与传统的迷宫密封相比,阻尼密封具有更好的封严性能和转子稳定性。传统迷宫密封和阻尼密封的泄漏量对转速变化不敏感,随进出口压差的增大而线性增大,不能满足火箭涡轮泵深度变推力(压差、转速显著变化)运行对离心轮凸肩间隙高效封严的需求。
1.1 一般资料 对 2008年1月至 2017年12月在海军军医大学(第二军医大学)长征医院及上海国际医学中心接受甲状腺结节微波消融治疗的2 857例患者(共 3 480 枚结节)进行随访,其中男 1 012例、女 1 845例,年龄为 15~62 岁,中位年龄为 43 岁。微波消融病例选择标准:(1)良性结节,如颈部明显隆凸表现、颈部压迫感明显、高功能腺瘤;(2)恶性结节,如局限在甲状腺包膜内的分化型甲状腺癌。本研究通过海军军医大学(第二军医大学)长征医院和上海国际医学中心伦理委员会审批。
螺旋密封的泄漏量对转速变化非常敏感,转速越高,泄漏量越小。这被解释为类似于螺杆泵的“泵送效应”:流体工质被螺旋槽泵送回密封进口以抵消一部分压差驱动的间隙泄漏;转速越高,螺旋槽泵送能力越强,泄漏量越小。Kanki等
首先实验研究了转子、静子表面和转/静两面均带有螺旋槽的3种螺旋密封的静、动态特性,实验表明,螺旋槽密封在液体旋转机械中具有优良的封严性能,特别是在高速下;转/静两面均带有螺旋槽的双螺旋密封具有更优的封严性能。Childs等
实验研究了螺旋角
对螺旋密封泄漏特性的影响,研究表明,
越大,螺旋密封泄漏量随转速增加而减小的速度更快。Watson等
实验表明,在高压差和高转速条件下,较大的螺旋角(
=15°~30°)可以获得更优的封严性能;由于螺旋密封的封严性能依赖于“泵送效应”,在低转速下封严性能较差,甚至不如光滑平面密封或其他传统密封。Li等
的实验和数值结果表明,螺旋密封的动力特性系数随转速变化显著,有效阻尼随转速的增大而显著减小,高转速下负的有效阻尼极易诱发转子涡动失稳。
针对上述传统密封形式的优缺点,一些学者开始关注组合型密封。Wisher等
提出了一种具有迷宫槽静子面(LGS)和螺旋槽转子面(GR)的组合密封(LGS/GR),研究表明,水工质下,组合密封LGS/GR比转子面有螺旋槽的螺旋密封(SS/GR)的泄漏量减少了45.3%。Li等
提出了孔型静子面/螺旋槽转子面(HPS/GR)和袋型静子面和螺旋槽转子面(PDS/GR)的两种组合密封,以水为工质,研究了两种组合密封在大压差(25 MPa)和不同转速(0.5×10
~8.0×10
r/min)下的泄漏特性和转子动力特性,结果表明,孔型静子面/螺旋槽转子面的组合密封(HPS/GR)的泄漏量最小,有效阻尼最高,尤其是在高转速下,有效阻尼随转速的增加而明显增大。
基于上述新型组合密封在高压差、高转速、高预旋等复杂变工况下的应用潜力,本文针对叶轮凸肩密封的封严性能优化方案,提出了一种孔型静子面与螺旋槽转子面组合的新型螺旋阻尼密封,同时提出了一种“双进口边界”数值计算模型来模拟高压力和高预旋速度工况。本文以某液体火箭发动机实际深度变推力运行时,液氧涡轮泵的6种变负载工况(23%~108%负载率)作为边界条件,在2种进口预旋比(
为0、0.75)时,计算分析了新型螺旋阻尼密封的泄漏量、流场结构和密封间隙内周向旋流速度分布,并与迷宫密封、孔型阻尼密封、双螺旋密封等3种传统动密封进行了比较研究。
1 计算模型
针对某液氧涡轮泵叶轮前凸肩密封结构,设计了迷宫密封、孔型密封和双螺旋密封,并发明了一种与孔型和双螺旋密封具有相同孔、槽几何尺寸的孔型静子面/螺旋槽转子面的新型螺旋阻尼密封,具体的结构示意图如图1所示。图2给出了3种常规密封(迷宫、孔型、双螺旋密封)和新型螺旋阻尼密封的三维计算模型和网格。图3给出了孔腔和螺旋槽的几何排布、尺寸参数示意图。4种密封结构具有相同的密封长度、直径和径向间隙。表1给出了4种密封结构的详细装配、几何尺寸。为保证研究具有可对比性,新型螺旋阻尼密封具有与孔型密封和双螺旋密封完全相同结构参数的静子面孔腔尺寸和排布、转子面螺旋槽和密封间隙。螺旋槽几何参数设计参考文献[19-20]中的槽宽、槽深、棱宽、螺旋角等参数优化结果。


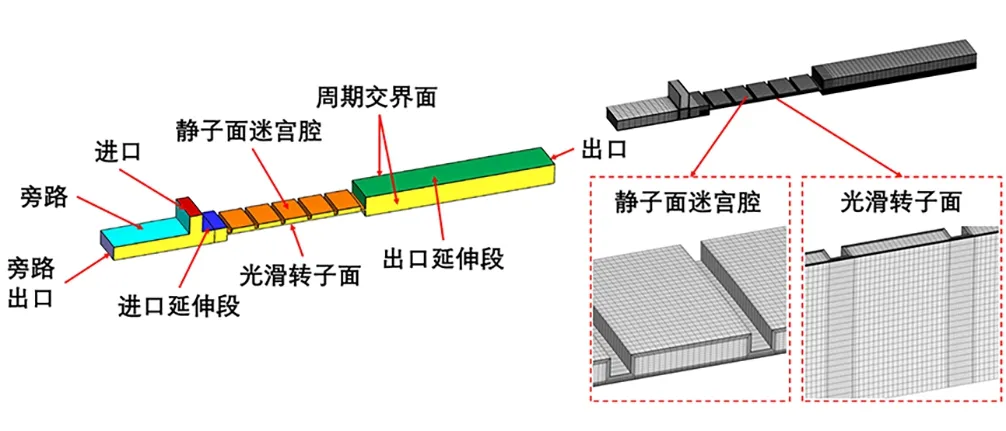

图5给出了孔型密封和螺旋密封的泄漏量随转速变化的数值预测结果与实验结果。在一定的进出口压差下,两种动密封的泄漏量均随着转速的升高而降低,变化趋势与实验结果完全一致。孔型密封泄漏量预测误差为2%~9%,螺旋密封在294 kPa压差工况下的泄漏量预测误差为5%~9%,在1 000 kPa压差工况下的泄漏量预测误差为4%~7%。结果表明,两种密封形式的数值预测结果偏差均低于10%,该数值预测方法在变压差、变转速工况下均能获得良好的预测精度。因此,本文采用的动密封泄漏特性数值预测方法对孔型密封和螺旋密封的泄漏量具有可靠的预测精度。
二十世纪六十年代初的一天凌晨,几百名警卫在柏林勃兰登堡门的分界线上各就各位,一道横贯东德和西德的冰冷墙壁隔绝了人们的交往。1984年,艺术家特里·诺尔趁守卫不注意,偷偷在灰白的柏林墙上涂鸦,开启了柏林墙的彩色生涯。十几年里,特里·诺尔和其他艺术家用长达一公里的涂鸦把柏林墙变成了艺术品,寄托了人们美好的愿望。冷战结束后,柏林墙被推倒,但在艺术家们的奔走下,涂鸦的部分被保留下来,这就是著名的“东边画廊”。
本文基于网格划分软件Ansys ICEM 18.0对密封计算域进行结构化网格划分,对迷宫和孔型密封腔室采用O网格进行边界层网格加密。4种密封的密封间隙均设置20个以上节点,网格具有良好的网格质量,在所有工况条件下主体计算域的最大
值均小于200,满足湍流模型的计算要求。
2 数值方法与验证
表2、表3分别给出了本文计算中液氧涡轮泵变负载运行工况下的前凸肩密封运行参数和采用的数值方法,两种进口预旋比
为0、0.75。基于商业软件Ansys CFX 18.0,以低温液氧为流动工质进行模拟计算。针对液氧涡轮泵离心轮凸肩密封大压差、高旋流的工况,本文提出了一种具有真实进口和旁路出口的“双进口边界”模型。设置计算域旁路出口静压模拟密封进口压力边界,设置计算域进口径向和切向速度模拟密封入口高预旋速度边界。这种双进口模型能够实现耦合控制密封入口的压力和速度边界条件,适用于高旋流、高压力的动密封进口工况模拟。
‘七七事变’后,国民政府收拢沿海的台籍人士,以‘关怀’为名,将散居在闽南沿海一带的四百多名台胞强行迁往闽北的崇安山区,成立了‘台民垦殖所’集中管理。


对于具有光滑转子面的迷宫和孔型密封,采用旋转壁面转速来模拟转子的旋转,整个计算域为静止域。对于双螺旋和螺旋阻尼密封,转子表面具有螺旋槽结构,是不光滑的非回转面,本文基于多重坐标系法,将动密封计算域分为旋转坐标系下的旋转域(转子螺旋槽)和静止坐标系下的静止域(静子螺旋槽/孔腔),采用冻结转子交界面来模拟静止域和旋转域之间的流体耦合流动。当均方根残差均小于10
,密封泄漏量监测值每百步变化率低于0.1%,且进出口质量流量不平衡度小于0.1%时,认为该计算收敛。涡轮泵负载率
的定义为
与AHP方案不同的是,AHT方案中外界输入热量进入蒸发器和发生器。故而,与AHP方案中采用相同的分析思路,必须保证蒸发器和发生器的换热效率。同时,本方案中吸收器和冷凝器的换热效果可通过平衡换热面积与锅炉给水(冷却水)流速来实现。
甲状旁腺正确辨认后其血供的保护是至关重要的。目前研究表明甲状腺全切术后暂时性甲状旁腺功能减退可能与甲状旁腺的血供障碍有关,因此推荐精细被膜解剖法。需要警惕的是,部分保留血供的甲状旁腺仍可因静脉回流障碍造成其淤血、坏死。对表面血管扩张、淤血明显者,需予以切除行I期自体移植。朱精强[10]强调对于A3型(完全位于甲状腺组织内)甲状旁腺及严重缺血、游离的甲状旁腺,自体移植是最后的弥补方法。
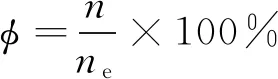
(1)
式中:
为转速;
为设计工况2下的额定转速。
为保证网格无关性,选用本文研究的孔型密封计算模型,生成网格数为23~119万的4套疏密不同的网格,在设计工况2下,以泄漏量为指标,检验网格无关性。网格加密按照
、
、
这3个方向同比例增加节点数的方式。图4给出了孔型密封泄漏量随网格节点数变化曲线。由图4可知,当网格节点数大于51万时,网格节点数增加引起的泄漏量预测值相对变化率约0.1%,对密封泄漏量的数值预测影响几乎可以忽略,认为此时已达到网格无关要求。迷宫、双螺旋和螺旋阻尼密封计算模型均参照该网格划分方式进行加密,最终的周期性模型网格节点数是:迷宫密封36万,孔型密封51万,双螺旋密封73万,螺旋阻尼密封105万。

高压超低温液氧工质动密封泄漏特性实验测试困难,目前无公开发表的液氧动密封泄漏量的实验数据。本文利用Jolly等
的孔型阻尼密封实验模型和Nagai等
的螺旋密封(静子面螺旋槽和光滑转子面)的实验数据,以水为工质,验证了动密封泄漏量数值预测方法的准确性。由于液氧和水都具有较强的不可压缩性,液氧涡轮泵常采用水压实验验证泵的水力性能,本文认为用水工质动密封实验数据验证液氧动密封数值方法是合理的。为了保证验证的可信性,数值验证的模型几何参数和运行条件与实验数据完全一致。
本文采用三维造型软件UG进行动密封计算域造型,考虑到动密封结构的旋转周期性,为方便网格划分并减小计算量,迷宫密封计算域选取5°的弧段,孔型密封选取了两排孔腔弧段,根据周向孔排数选取5°弧段作为计算域。双螺旋和螺旋阻尼密封根据螺纹头数选取10°的周期弧段。两侧周期面均采用旋转周期性边界条件。为保证进、出口均匀边界的合理性,密封计算域的进出口均分别适当设有延伸段。

3 结果与讨论
本文对4种动密封方案的泄漏特性、流场结构和旋流速度分布进行了分析比较,通过对静子面孔腔和转子面螺旋槽的子午面上速度流线和泵送速度的分析,阐明了各动密封封严性能差异的原因和新型螺旋阻尼密封的封严机理。
3.1 泄漏特性
图6给出了当进口预旋比
为0.75时(实际运行的涡轮泵离心轮前凸肩密封进口预旋比为0.60~0.80),4种动密封方案的泄漏量随负载率变化曲线(
=23%,31%,54%,77%,100%,108%)。由图6可知,4种动密封方案的泄漏量均随负载率的增大而增加,这主要是由于负载率的增加伴随着压差的增大。双螺旋和螺旋阻尼密封泄漏量随负载的增长速率明显低于迷宫和孔型密封,这主要由于转速的增加(螺旋槽“泵送效应”增强)对两种转子面带螺旋槽的密封结构的封严性能起到了增强作用。高负载工况(高压差、高转速)下,双螺旋和螺旋阻尼密封在封严性能上优势更明显。
在公路项目建设过程中,会用到各种各样的机械设备,而机械设备的配置与维护方式是否妥当,直接影响到建设工程的顺利开展。工程机械设备配置以及维护管理对于工程施工质量产生的影响很大,因此在施工过程中必须按照工程项目的特点,做好机械设备的配置以及维护管理工作,从而保证公路工程的建设水平达到设计要求。
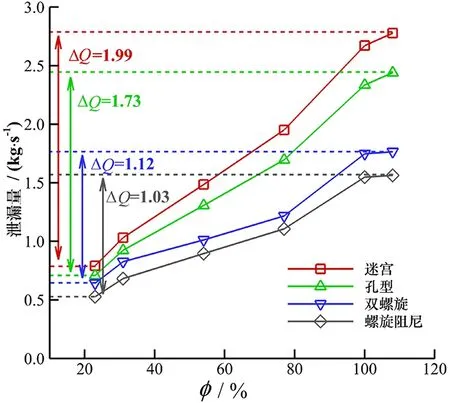
文献[7-8]证明:传统螺旋密封的封严性能在很大程度上取决于叶轮机械的运行转速,在低转速下封严性能较差。由图6可知,在低转速(9 000、12 000 r/min)的工况5、工况6下,双螺旋密封的泄漏量与孔型密封非常接近,分别仅比孔型密封降低了10%和9.4%,而在工况1~4下,泄漏量降低了22%~28%,这主要是由于较低的转速(弱“泵送效应”)会削弱双螺旋密封的封严性能。
460 Surgical treatment of intracerebral hemorrhage in uremia patients undergoing dialysis
总体而言,4种动密封结构的封严性能优劣依次为螺旋阻尼密封、双螺旋密封、孔型密封、迷宫密封。在6种变负载工况下,螺旋阻尼密封的泄漏量分别比迷宫、孔型和双螺旋密封降低了33%~44%、25%~36%、9%~18%。设计工况下(工况2,
=100%),相比3种常规密封的减幅分别为42%、33.7%、12%。结果表明,螺旋阻尼密封在所有负载工况(
=23%~108%)下的泄漏量都最低,且与双螺旋密封相比,螺旋阻尼密封的封严性能对转速的敏感度更低,即使在低转速下也能保持最低的泄漏量。因此,新型螺旋阻尼密封具有最佳的封严性能和优良的变工况(变压差、变转速)适应能力。
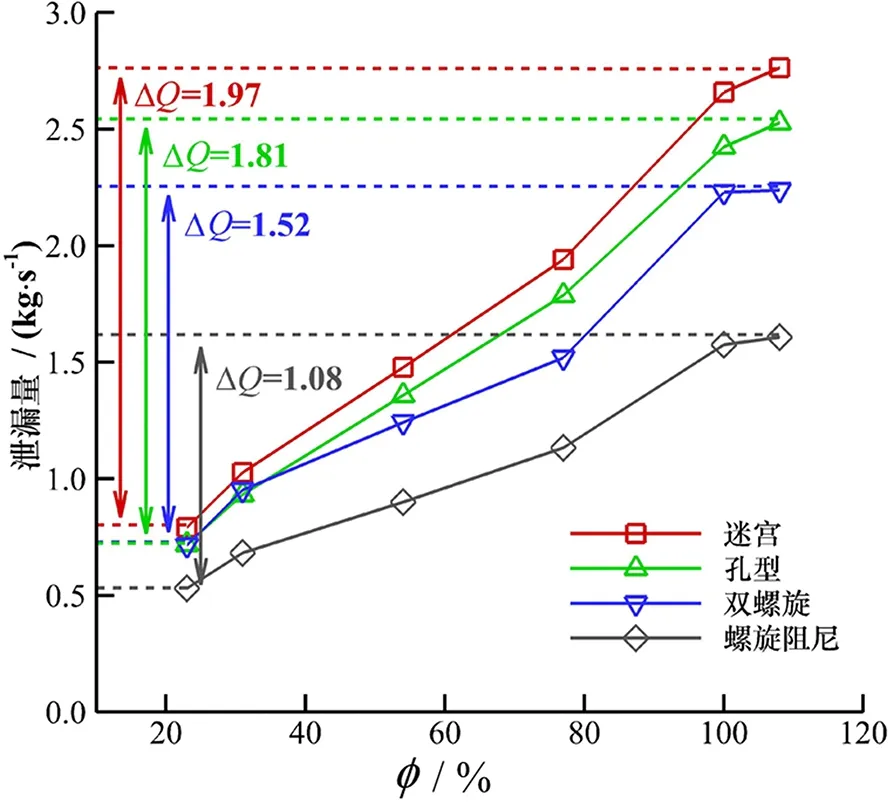
图6、图7中垂直方向箭头的右端给出了当负载率从23%增大到108%时,4种动密封泄漏量的绝对变化量。螺旋阻尼密封由于火箭发动机变推力(涡轮泵变负载)引起的泄漏量变化量最小,当
=0时,相比迷宫、孔型、双螺旋密封的变化量分别减小了45%、40%、29%;当
=0.75时,分别减小了48%、40%、8%。新型螺旋阻尼密封由于进口预旋(
=0~0.75)引起的泄漏量绝对值变化最大为0.04 kg/s,相对变化量为2.7%,相比孔型阻尼密封和双螺旋密封的最大相对变化量减小了50%、88%。
图7给出了当进口预旋比
=0时(在动密封上游安装防旋板或反向射流器等止旋装置可有效抑制密封进口旋流),4种动密封方案的泄漏量随负载率变化曲线。由图6、图7可知,在本文计算的变负载工况下,迷宫密封的泄漏量随进口预旋比的增加几乎不变,孔型、双螺旋和螺旋阻尼密封都因进口预旋比的增大而不同程度地减小。当进口预旋比
=0.75时,相比无预旋情况,孔型、双螺旋和螺旋阻尼密封的泄漏量分别降低了0.9%~5.3%、10%~22%、0.05%~2.7%,可知双螺旋密封泄漏特性对进口预旋极其敏感,进口止旋装置会导致双螺旋密封泄漏量显著增大,而新型螺旋阻尼密封泄漏特性对进口预旋变化不敏感,可忽略进口预旋的影响。
资料显示,军庄镇的地层主要为古生界的奥陶系和石炭系、二叠系,在奥陶系与石炭、二叠系之间存在平行不整合接触关系,向斜构造明显[4],其中石炭系、二叠系地层单位均是以本地区地名命名[5],岩层中植物化石丰富[6-7].
综上所述,新型螺旋阻尼密封各工况下均具有最佳的封严性能,且其泄漏量对于压差、转速、进口预旋等工况条件变化的敏感性最低,具有优良的变工况适应能力,能够满足液氧涡轮泵深度变推力下的封严需求,是一种理想的液氧涡轮泵离心轮凸肩密封结构。
3.2 耗散效应
图8中红色虚线表示孔腔内的涡流结构,白色箭头表示进入孔腔内流体的流入方向,红色字母
表示流入方向与水平轴向的夹角,定义为入射角。入射角
越大,代表流入腔室的流量越大,在腔室内耗散的能量也越大。由图8(a)中的孔型密封流场可见,液体通过一个小入射角(左图)直接流入腔室或先经过一个小壁面涡(右图),然后在腔室右上角形成一个约1/3~2/3腔室大小的涡流,其余的液体直接流出腔室,动能未被耗散。部分孔腔内不会形成大的涡流,大量的流体直接沿接近径向方向流出孔腔(中间图)。图8(b)的螺旋阻尼密封流场中,当螺旋槽位于孔腔之前时(左图),由于螺旋槽和间隙中较高的泵送速度和离心速度,流体在壁面涡的作用下,以一个比孔型密封更大的入射角
进入孔腔,流入腔室的流量更多,在腔室耗散的动能也更多。当螺旋槽与空腔并排时(中间图),入流不仅流过间隙,而且流过大部分的螺旋槽区域,该情况也具有较大的
和较大的质量流量。当螺旋槽位于孔腔之后(右图),螺旋槽可以增强孔腔内的涡流耗散。如图8(b)所示,其流动与传统孔型密封类似,但与孔型密封相比,涡流结构更大、更稳定,几乎覆盖了整个孔腔。
力争水利管理改革实现新突破。进一步完善水利规划体系、法治体系和科技支撑体系,全面推进依法治水和科技兴水;加快水资源管理体制、水利建设与运行管理体制、水利投融资机制、水价形成机制、基层水利服务体系等重点领域和关键环节改革攻坚,建立水资源有偿使用制度和水生态补偿制度;继续推进首批30个节水型社会建设重点县建设;全面推进农业水价综合改革等工作。
图8给出了孔型密封和螺旋阻尼密封的3种典型孔腔子午面上的速度流场和流线分布。孔型密封由于光滑转子表面和孔腔的交错排布方式,整个密封流场可以通过两排孔腔的子午面来反映。孔型密封孔腔子午面的速度流场和流线分布主要表现为图8(a)中的3种典型形式。但对螺旋阻尼密封,由于转子表面不光滑,螺旋槽的轴向位置相对于孔腔变化会造成孔腔内不同的流场分布。为了准确研究螺旋槽对孔腔流场的影响,选取了3个典型的孔腔螺旋槽子午面,螺旋槽相对于孔腔处于3种不同的位置,依次为螺旋槽在孔腔之前、螺旋槽与孔腔并排、螺旋槽在孔腔之后。

文献[17-18]指出:孔型阻尼密封间隙内流体压力能转化为动能,高速射流进入孔腔,通过动能耗散将压力能转化为内能,降低泄漏量。由于具有孔腔结构的“粗糙”的静子表面和具有螺旋槽结构的转子表面对间隙泄漏流的耦合作用,螺旋阻尼密封的孔腔耗散效应与孔型密封不同。为了阐明螺旋阻尼密封与孔型密封腔室耗散作用的差异,对两种动密封的孔腔内详细流场结构进行了分析。
在郭村我也拍过一些人,并因此记住了他们的模样。再次去郭村,路上遇见会有特别的亲切感,仿佛他们是我住在乡下的亲人。
综上所述,螺旋阻尼密封转子表面不同相对位置的螺旋槽对静子表面的孔腔耗散效应都具有增强的作用。由于难以定量地分析孔腔内的耗散效应,对孔腔内流场的分析不足以解释螺旋阻尼密封具有更优的封严性能的内在机制。
3.3 泵送效应
图9为静子和转子表面的螺旋槽周向展开图,上半象限为静子表面,下半象限为转子表面。灰色部分代表螺旋棱,白色部分代表螺旋槽。
表示螺旋角,本文计算模型为21.21°。对于传统的双螺旋密封,静子表面和转子表面的螺旋槽的旋向相反,因此平行于槽方向的速度计算方法也不同。
为了定量地分析螺旋阻尼密封的封严机理,本文计算了转子面螺旋槽内的平均泵送速度。文献[8-10]研究表明,螺旋密封的封严机理是通过螺旋槽内的“泵送效应”来实现的。在Iwatsubo等
提出的平行和垂直于螺旋槽方向的直角坐标系基础上,本文用流体平行于螺旋槽的速度分量来表征螺旋槽“泵送效应”的强度和方向。

假设旋转方向、
轴正向和指向出口的方向为正,则平行于静子槽速度
和平行于转子槽速度
分别定义为

(2)
式中:
、
分别是流体空间中某点的相对轴向速度和相对周向速度;
为相对于静止坐标系;
为相对于旋转坐标系。负值的
、
表示流体是在相对于螺旋槽被反向泵送到密封进口,正值表示流体是在相对于螺旋槽向密封出口泄漏,负值的
、
也可以被定义为泵送速度,泵送速度的绝对值越大说明泵送效果越明显,封严性能越好。轴向速度
可以直接从CFX结果文件中导出,周向速度
需要用户自定义求解,即

(3)
的求解需要在旋转圆柱坐标系中进行速度变换,图10给出了详细的转换示意图。考虑到带有螺旋槽的转子表面的旋转,
的求解应采用旋转坐标系下的相对速度。旋转方向遵循右手规则,旋转方向被定义为正,周向速度被定义在式(3)中,(
,
)表示空间坐标系中的坐标,(
,
)表示旋转坐标系中的相对速度,这4个变量都可以在CFX结果中得到。

为了准确比较双螺旋密封和螺旋阻尼密封转子表面螺旋槽的泵送效应强度,阐明螺旋阻尼密封螺旋槽的封严机理,需要进一步对螺旋槽内流体速度进行定量分析。图11给出了双螺旋和螺旋阻尼密封某子午面上的
云图分布,图中红色虚线框中的旋转域被选作分析对象。图12给出了双螺旋和螺旋阻尼密封在6种变负载工况下的线平均
随
变化的分布曲线,其中
表示到槽底的距离。双螺旋密封的
为负值,随着负载率的增加而减小,泵送速度-
增大,这主要是由于泵送效果随着转速的增加而增强。在图12(b)中,螺旋阻尼密封的
为负值,随着负载率的增加而减小,泵送速度-
增大且数值和增幅均比双螺旋密封大。螺旋阻尼密封的
沿径向方向变化不明显,间隙附近的
显著降低,这意味着泵送速度-
迅速增加,泵送效果在间隙处达到最大。一般情况下,双螺旋和螺旋阻尼密封的
几乎在所有工况下均为负值,这表明所有螺旋槽内流动都表现为反向泵送。螺旋阻尼密封在全工况下的泵速-
均大于双螺旋密封,尤其是在高负载工况下(高压降、高转速)。

为了研究
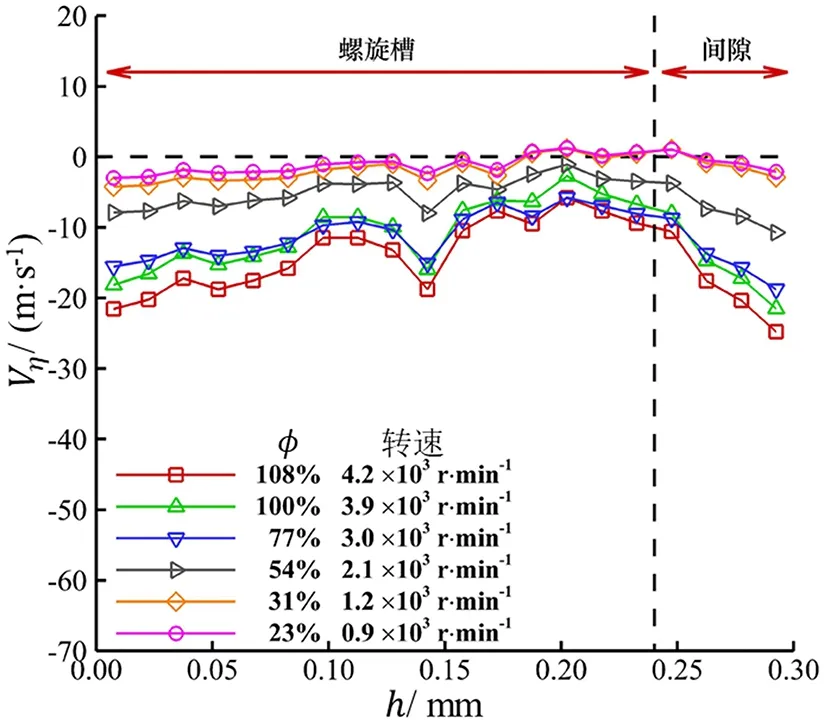
沿轴向的变化规律,本文同样将图11中红色虚线框中的螺旋槽旋转域作为分析对象。图13给出了双螺旋和螺旋阻尼密封在6种变负载工况下
随
变化的分布曲线,其中
表示到密封入口的轴向距离。双螺旋密封的平均
值沿轴向位置变化较大,且随槽、棱的位置交替变化明显,具有明显的周期性特征。
在螺旋棱区域从一个接近于零的极小正值开始,进入螺旋槽区域后从槽前壁处开始迅速增加到一个幅值,然后在靠近后壁处迅速减小,直到在螺旋棱处下降到接近于初始值。而对于螺旋阻尼密封,则没有明显的周期性和变化规律,
随轴向位置的变化在一定范围内振荡。从图13中可以得到与图12相同的结论,对于双螺旋和螺旋阻尼密封的转子面螺旋槽,几乎所有工况下的
都为负值,这意味着槽内流动表现为反向泵送。螺旋阻尼密封的泵送速度-
在全工况下均大于双螺旋密封,特别是在高负载工况下(高压差、高转速)。以设计工况2为例,双螺旋密封沿轴向分布的
平均值约为20 m/s,螺旋阻尼密封沿轴向分布的
平均值约为50 m/s,约为双螺旋密封的2.5倍,增大150%。由此可见,螺旋阻尼密封的转子面螺旋槽的泵送作用远强于双螺旋密封,具有更优的封严性能。这主要是由于定子表面的孔腔的结构,阻碍了泄漏流圆周速度的发展,导致本身为负值的相对圆周速度
的绝对值显著增加。

3.4 周向旋流速度
文献[23-25]指出,减小密封腔室和间隙内周向旋流速度能够有效增大动密封有效阻尼。传统的直通式迷宫密封由于无法抑制周向旋流的发展,通常会产生较大的交叉刚度,降低系统的有效阻尼,易诱发转子振动失稳;阻尼密封粗糙静子面能有效减小密封间隙内的周向旋流速度,增大有效阻尼,增强轴系稳定性。
图14给出了4种密封结构在密封间隙内的周向旋流速度沿轴向的分布曲线(
=100%,
=0.75)。总体来看,密封间隙内的周向旋流速度由大到小的顺序为迷宫、双螺旋、孔型、螺旋阻尼密封。迷宫密封的间隙旋流速度从密封进口到出口均匀缓慢减小,双螺旋密封的间隙旋流速度随着螺旋槽、棱的交替而呈现出近似周期性变化。孔型密封和双螺旋密封的间隙旋流速度相对迷宫、双螺旋密封更小,但孔型密封的间隙旋流速度在前半段有一个激增,导致孔型密封的整体平均间隙旋流速度高于新型螺旋阻尼密封。较低的周向旋流速度能够有效地减小密封的交叉刚度系数,从而增大系统的有效阻尼,有利于转子系统的抑振增稳。从周向旋流发展来看,螺旋阻尼密封具有最低的平均间隙旋流速度,需进一步开展其转子动力特性的评估研究。

4 结 论
本文针对液氧涡轮泵叶轮前凸肩密封提出了一种新型的螺旋阻尼密封(静子面孔型和转子面螺旋槽)。针对高预旋速度和高压力来流条件的模拟,提出了一种“双进口边界”数值模型,可实现动密封进口压力和速度边界条件的耦合控制。对比研究了迷宫密封、孔型阻尼密封、双螺旋密封等3种传统动密封结构和新型螺旋阻尼密封在某液氧涡轮泵6种变负载运行工况(负载率
=23%,31%,54%,77%,100%,108%)、2种进口预旋比(
=0,0.75)下的泄漏特性,得到如下主要结论。
(1)4种动密封方案的封严性能依次表现为螺旋阻尼密封、双螺旋密封、孔型密封、迷宫密封。新型螺旋阻尼密封各工况下均具有最佳的封严性能,且其泄漏量对于压差、转速、进口预旋等工况条件变化的敏感性最低,具有优良的变工况适应能力,能够满足液氧涡轮泵深度变推力下的封严需求,是一种理想的液氧涡轮泵离心轮凸肩密封结构。
(2)双螺旋密封泄漏特性对进口预旋极其敏感,进口止旋装置会导致双螺旋密封泄漏量显著增大,而新型螺旋阻尼密封泄漏特性对进口预旋变化不敏感(<2.7%),可忽略进口预旋的影响。
(3)螺旋阻尼密封的转子面螺旋槽对静子面孔腔内涡流耗散具有增强作用,增加了入射角
和入流流量,稳定加强了耗散涡流强度,最终增强了耗散作用,降低了泄漏量。
(4)螺旋阻尼密封转子螺旋槽子午面上的
在全工况下均为负值,槽内流动表现为反向泵送。静子面上的孔腔也能增强转子面螺旋槽内的泵送效应,在设计工况2下,螺旋阻尼密封转子槽内的泵送速度-
约为双螺旋密封的2.5倍,增大了150%。
(5)4种动密封方案中,新型螺旋阻尼密封的平均间隙周向旋流速度最小,可有效降低密封的交叉刚度、增大有效阻尼,有利于转子系统的抑振增稳。
:
[1] 张琛. 火箭发动机涡轮泵机械密封的磨损机理及性能优化 [D]. 西安: 西安理工大学, 2019.
[2] 尹源, 廖传军, 王志峰, 等. 火箭涡轮泵机械密封研究综述 [J]. 宇航总体技术, 2017, 1(3): 54-60.
YIN Yuan, LIAO Chuanjun, WANG Zhifeng, et al. A review of mechanical face seal in rocket turbopump [J]. Astronautical Systems Engineering Technology, 2017, 1(3): 54-60.
[3] 张远君. 液体火箭发动机涡轮泵设计 [M]. 北京: 北京航空航天大学出版社, 1995.
[4] WATSON C, WOOD H. Evaluating configurations of double surface helical groove seals using computational fluid dynamics [C]∥ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition. New York, NY, USA: ASME, 2018: V02CT42A 053.
[5] VANCE J M, MURPHY B, ZEIDAN F. Machinery vibration and rotordynamics [M]. Hoboken: Wiley, 2010.
[6] 李志刚. 袋型阻尼密封泄漏特性和转子动力特性的研究 [D]. 西安: 西安交通大学, 2013.
[7] KANKI H, KAWAKAMI T. Experimental study on the static and dynamic characteristics of screw grooved seals [J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1988, 110(3): 326-331.
[8] IWATSUBO T, SHENG B C, ONO M. Experiment of static and dynamic characteristics of spiral grooved seals [EB/OL]. (1991-10-01)[2021-12-12]. https:∥ntrs.nasa.gov/search.jsp?R=19920005143.
[9] IWATSUBO H, NISHINO T, ISHIMARU H. A study on dynamic characteristics of double spiral grooved seals [EB/OL]. [2021-12-12]. https:∥jglobal.jst.go.jp/en/detail?JGLOBAL_ID=2009021020 72792369.
[10] CHILDS D W, NOLAN S A, KILGORE J J. Test results for turbulent annular seals, using smooth rotors and helically grooved stators [J]. Journal of Tribology, 1990, 112(2): 254-258.
[11] WATSON C, WOOD H G. Optimizing a helical groove seal with grooves on both the rotor and stator surfaces [C]∥ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition. New York, NY, USA: ASME, 2017: V02BT41A044.
[12] WATSON C, WOOD H G. Developing an optimal helix angle as a function of pressure for helical groove seals [C]∥ASME 2017 Fluids Engineering Division Summer Meeting. New York, NY, USA: ASME, 2017: V01AT05A020.
[13] NAGAI K, KANEKO S, TAURA H, et al. Numerical and experimental analyses of static characteristics for liquid annular seals with helical grooves in seal stator [J]. Journal of Tribology, 2018, 140(3): 032201.
[14] LI Zhigang, FANG Zhi, LI Jun, et al. Numerical modeling of static and rotordynamic characteristics for three types of helically grooved liquid annular seals [J]. Journal of Vibration and Acoustics, 2020, 142(4): 041001.
[15] PAUDEL W, WATSON C, WOOD H G. Mixed helical labyrinth groove seal optimization using computational fluid dynamics [C]∥ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition. New York, NY, USA: ASME, 2017: V02BT41A 004.
[16] PAUDEL W, WATSON C, WOOD H G. The impact of adding a labyrinth surface to an optimal helical seal design [C]∥ASME 2018 International Mechanical Engineering Congress and Exposition. New York, NY, USA: ASME, 2018: V007T09A092.
[17] FANG Zhi, LI Zhigang, LI Jun, et al. Numerical investigation on the static and rotordynamic characteristics for two types of novel mixed helical groove seals [C]∥ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition. New York, NY, USA: ASME, 2020: V10AT25A036.
[18] LI Zhigang, FANG Zhi, LI Jun, et al. Static and rotordynamic characteristics for two types of novel mixed liquid damper seals with hole-pattern/pocket-textured stator and helically grooved rotor [J]. Journal of Engineering for Gas Turbines and Power, 2021, 143(4): 041019.
[19] 杨晓宗. 几何参数对螺旋密封性能影响的研究 [D]. 上海: 华东理工大学, 2014.
[20] 李建忠. 离心泵用螺旋密封性能研究 [D]. 兰州: 兰州理工大学, 2019.
[21] JOLLY P, ARGHIR M, BONNEAU O, et al. Experimental and theoretical rotordynamic coefficients of smooth and round-hole pattern water-fed annular seals [J]. Journal of Engineering for Gas Turbines and Power, 2018, 140(11): 112501.
[22] NAGAI K, KOISO K, KANEKO S, et al. Numerical and experimental analyses of static and dynamic characteristics for partially helically grooved liquid annular seals [J]. Journal of Tribology, 2019, 141(2): 022201.
[23] 薛文松, 方志, 王天昊, 等. 防旋板结构的迷宫密封转子动力特性研究 [J]. 西安交通大学学报, 2022, 56(3): 105-116.
XUE Wensong, FANG Zhi, WANG Tianhao, et al. Investigation on the rotordynamic characteristics of labyrinth seal with swirl brakes [J]. Journal of Xi’an Jiaotong University, 2022, 56(3): 105-116.
[24] 李志刚, 方志, 李军. 液相和多相环境下环形动密封泄漏流动和转子动力特性的研究进展 [J]. 西安交通大学学报, 2020, 54(9): 1-22.
LI Zhigang, FANG Zhi, LI Jun. Review of the leakage flow and rotordynamic characteristics of the annular dynamic seals in liquid and multiple phases conditions [J]. Journal of Xi’an Jiaotong University, 2020, 54(9): 1-22.
[25] 王天昊, 李志刚, 李军. 采用Bulk-Flow模型的直通式迷宫密封转子动力特性研究 [J]. 西安交通大学学报, 2021, 55(5): 25-33.
WANG Tianhao, LI Zhigang, LI Jun. Investigation on the rotordynamic characteristics of straight-through labyrinth seal using Bulk-Flow model [J]. Journal of Xi’an Jiaotong University, 2021, 55(5): 25-33.

