采用天鹰优化卷积神经网络的精密数控机床主轴热误差建模
李国龙,陈孝勇,李喆裕,徐凯,唐晓东,王志远
(重庆大学机械传动国家重点实验室,400044,重庆)
数控机床作为加工高精度齿轮的高端装备,其精度极大地影响齿轮产品的优劣程度。目前,磨齿机精度已达到微米级,然而受到多种因素的影响,其精度稳定性只能达到丝级。其中,热误差是影响机床精度稳定性的主要因素之一[1]。现有研究显示,几何误差的研究已经相对成熟[2-3],在精密加工过程中,热误差约占制造总误差的40%~70%[4-7],并且磨齿机的精度越高,热误差占比就越大[8]。其中,导致磨齿机热误差最主要因素之一是主轴的热变形。因此,减小数控机床主轴热误差对保证高精密加工具有重要的意义。
热误差补偿作为一项十分有效、经济的提高数控机床精度的技术[9-10],其关键在于建立一个准确、稳定的热误差预测模型。国内外学者对热误差建模做了大量的研究。Huang等[11]利用遗传算法(genetic algorithm optimization,GA)对BP(back propagation,BP)神经网络的初始权值和阈值进行优化,建立了基于BP神经网络的高速主轴热误差模型,使预测的精度大大提高。Yang J.等[12]提出了基于模糊聚类的最小二乘支持向量机(least square support vector machine,LS-SVM)电动主轴热误差模型,结果表明该模型具有较高的预测能力,但是在环境温度变化以及不断加工后,其模型的预测精度会降低。魏新园等[13]基于全年环境温度下的多批次热误差实验数据,建立热误差偏最小二乘回归预测模型,结果表明所提的热误差稳健建模算法能够在环境温度变化较大时保持高预测精度和高稳健性。Yang B.等[14]基于改进的灰狼优化器(improved gray wolf optimizer,IGWO)和自适应神经模糊推理系统(adaptive neuro-fuzzy inference system,ANFIS),提出了一种精确的热误差模型,结果表明改进模型具有更好的鲁棒性、泛化性和稳定性。Li等[15]利用鲸鱼优化算法优化的支持向量机建立了热误差模型,提高了模型预测精度。张毅等[16]提出一种基于灰色理论预处理的神经网络机床热误差补偿模型,该模型结合多种算法的优点,有效地避免了数学模型丢失信息的缺点。Cao等[17]推导了工件热变形误差的理论模型,建立了基于多元线性回归(multiple linear regression,MLR)的热误差补偿模型。补偿后,滚齿加工的齿厚误差范围减小到-4~8 μm,表明了热误差补偿模型的有效性。
普通的多元线性回归模型(MLR)虽然计算较快,但难以解决复杂的非线性映射关系。BP神经网络和SVM等方法虽然具有较强的非线性映射能力,但可能会收敛于局部最小值。而且,随着数据样本量越来越大,出现了拟合精度有限、程序运算缓慢等不足的问题。随着大数据、人工智能算法以及计算机性能的提升,传统的机器学习热误差模型不能满足数控机床主轴热误差预测精度的要求。
针对上述问题,本文提出了一种数据驱动的天鹰优化卷积神经网络(aquila optimizer-convolutional neural network,AO-CNN)热误差预测模型,将温度和热误差数据转变为数组的集合,以图片的形式输入到AO-CNN模型中,针对数控机床主轴的X向热变形,建立数控机床主轴的AO-CNN热误差预测模型,实现了对数控机床热误差的有效预测。CNN在开发全局解上具有优越性,能避免局部最优,可以解决较大样本下复杂的非线性问题,而且卷积核的存在减小了CNN中各层连接,简化了模型,也减小了过拟合的风险。一般情况下,CNN的卷积核越大识别的特征越好,但是过大的卷积核会导致计算量的暴增,不利于模型深度的增加,计算性能也会降低,因此采用天鹰优化算法得到最优卷积核。
1 磨齿机主轴热变形与磨齿加工分析
磨齿机主轴热误差是内外热源共同影响下的综合结果[18-19]。在电主轴的电机功率损耗和轴承处的摩擦产生大量热量以及外部环境温度的影响下,磨齿机主轴发生热变形,改变了砂轮与工件的相对位置。磨齿机主轴刀杆受热发生轴向和径向的热膨胀,如图1所示。主轴系统(由电主轴、轴承、冷却管、大托座、小托座、大立柱组成)产生大量的热同时传递到大小托座等主轴支撑部件上,使大小托座发生变形,引起主轴发生径向热漂移,这也是主轴系统X方向热误差的最主要成因。

图1 主轴热变形示意图
齿轮磨削加工具有径向进给运动、轴向冲程运动以及窜刀运动共3个运动。
X方向运动用于径向进给,将由热误差引起的砂轮与工件之间在X方向的热漂移定义为δx,以此反映中心距离的误差,如图2所示。热误差δx会引起工件的齿距偏差(Δfpt),影响齿轮传动的平稳性精度。并且,当热误差δx存在时,切割点从K移动到K′,KK′线垂直于齿轮铰孔,定义为齿廓总误差,如图3所示。KK′的计算公式[20]可表示为

图2 磨齿机热误差示意图

图3 砂轮沿X方向移动后切割点的位置变化
Fα=KK′=δxsinα
(1)
式中:Fα表示齿形总误差;α是KK′与水平方向之间的夹角。误差Fα会导致齿顶、齿根、齿厚、顶圆和齿根圆直径的变化。
Y方向运动用于调整砂轮窜刀方向,使新的切刃总是可以对准创成侧,影响着刀具的使用寿命,在加工过程中Y轴一般不移动,热误差对其产生的影响很小。Z方向为冲程运动,刀具沿工件齿宽方向的进给方向,对齿面的加工误差的影响较小。
由上述分析可知,齿轮加工精度受X方向误差影响最大。因此,本文主要研究磨齿机主轴系统X方向的热误差。
2 热误差建模
2.1 基于模糊C均值聚类的温度测点优化
温度敏感点的选择是热误差建模的基础,过多的温度点会导致多个温度变量之间的多重共线性问题,温度点过少可能会导致温度和热误差之间的映射不完整。此外,温度点的不合理组合也会降低热误差模型的预测性能。为了解决上述问题和减小计算量,采用模糊聚类算法和相关系数法筛选出关键温度点。
2.1.1 模糊C均值聚类
模糊C均值聚类(fuzzy C-means clustering,FCM)通过最小化目标函数来得到聚类中心,目标函数本质上是各个点到各个类的欧式距离的误差平方和。FCM将n个样本的数据集合X=(x1,…,xn)分为C个模糊组,并求C个模糊组的聚类中心矩阵ci={c1,…,cc}和一个C×N的一个隶属度矩阵U={uij},uij表示第j个数据点属于第i类的隶属度。根据得到的聚类中心,利用uij更新隶属度值。再利用
(2)
计算出目标函数Jm(U,X),记为j(t)(t为循环次数)。式中:X为具有N元的数据集合;m为聚类数;N为样本数。如果‖j(t)-j(t-1)‖<&,则停止迭代,否则重复上述步骤,直至满足循环停止条件。
Calinski-Harabasz(CH)指数[21]通过计算基于平均簇间和簇内平方和的分离度和紧密度来评定聚类效果,Milligan等[22]通过实验研究分析认为,使用CH指标确定最佳聚类数具有较好的效果,其公式为
(3)
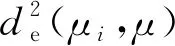
按聚类数从小到大分别计算CH值,CH最大时的聚类数即为最佳聚类数。聚类的过程就是最小化目标函数式(2)的过程,逐步降低目标函数的误差,当目标函数收敛时,便可得到最终的聚类结果[23]。
对目标函数求解后可以得到模糊矩阵U与聚类中心c
(4)
(5)
式中:cj表示第j个聚类中心;xi表示i个样本;uij表示样本xi属于cj的概率,即隶属度;dij为xi与第j个数据点间的欧几里德距离。
2.1.2 相关系数法
本文使用了卡尔·皮尔逊的相关系数法来计算热误差数据和温度变量之间相关性,选取温度变量与热误差变量相关性强的点作为关键温度点。计算公式为
(6)
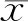
2.2 基于AO-CNN的热误差建模
2.2.1 天鹰优化算法
天鹰优化算法(AO)具有高可靠性和一致性[24],具有强大的最优解求解能力,能够以较快的加速度收敛和较强的稳定性进行寻优。天鹰算法优化步骤如下。
步骤1垂直俯冲 当天鹰识别猎物区域时,通过高空翱翔在全局初步选择最佳狩猎区域,以确定最优解的所在的搜索空间,公式为
(7)
式中:X1(t+1)为t+1代的解;Xbest(t)是最佳解,表示目标猎物的最近位置;t和T分别表示当前迭代和最大迭代次数;XM(t)表示在第t次迭代时当前解的位置均值;ε为0到1之间的随机值;Dim为问题的维度大小。
步骤2短滑翔攻击 当从高处翱翔中发现猎物区域时,天鹰在目标猎物上方盘旋,以缩小狩猎区域,即减小最优解的搜索空间,公式为
(8)
式中:XR(t)为[1,N]之间的随机解;D为维度空间;L(D)为捕猎飞行分布函数。
步骤3低空飞行 当精准确定猎物区域,并且天鹰准备着陆和攻击时,天鹰在选定的目标区域通过低飞慢降的攻击方式试探猎物的反应,缓慢接近目标,公式为
X3(t+1)=(Xbest(t)-XM(t))α-ε+
((UB-LB)ε+LB)δ
(9)
式中:α、δ为调整参数,由于本文热误差数据值偏小,固定为较小值0.1;UB和LB分别表示给定问题的上界和下界。
步骤4行走抓捕 当天鹰接近目标时,根据猎物的运动从陆地上空攻击猎物,进行快速收敛,公式为
(10)
式中:QF为用于均衡搜索策略的质量函数;G1表示在追捕猎物中天鹰的各种运动;G2代表天鹰在捕猎过程中的飞行斜率;X(t)为第t次迭代的当前解。
2.2.2 卷积神经网络
卷积神经网络具有极强的适应性,善于挖掘数据局部特征[25-26],提取全局训练特征和分类。CNN结构由输入层、卷积层、池化层、全连接层和输出层组成。在开发的CNN结构中,采用两层卷积层和池化层交替处理输入的数据,如图4所示。

图4 CNN卷积神经网络模型结构
卷积层神经元数学表达式为
(11)

池化层数学表达式为
(12)
式中:pool为池化函数;a和b对应表示每个特征图层不同的偏差值。
全连接运算的公式为
y=f2(αΣmi+b)
(13)
式中:y表示全连接运算的整合输出;α和b分别代表全连接运算的权值和偏置系数。
2.2.3 AO-CNN
卷积核作为CNN最重要的参数,直接影响热误差建模的准确性和稳定性,将CNN的卷积步长输入至AO算法中,通过反复迭代寻优,设置目标函数作为判断依据计算出预测性能最佳的卷积步长。AO-CNN训练流程如图5所示。详细步骤如下。

图5 AO-CNN训练流程
(1)将经过筛选后的关键温度点数据转化为一维像素矩阵。
(2)由于电涡流传感器采集的数据以电压的形式储存,首先将采集到的电压信号按标定值转换为热误差数据,再将一维数组形式转换为多维矩阵的格式。
(3)使用天鹰优化算法训练卷积神经网络的卷积核,以寻优出最佳的卷积步长。首先,随机初始化种群,确定种群规模X。其次,根据迭代的次数以及产生的随机数以获得最佳的寻优路径。最后,计算适应度函数值,将最佳卷积核大小输入到卷积层。
(4)利用优化后的卷积核大小用卷积神经网络进行训练,将数字矩阵依次输入卷积层、池化层、全连接层。卷积神经元提取能够提取训练数据的温度特征。
(5)计算输出后的结果损失函数,通过梯度下降原理更新权值,实现CNN的多次迭代计算,使预测模型逐渐收敛。
(6)经过多次迭代后,使用测试数据集来判断AO-CNN的预测性能。
(7)根据性能评估结果,对神经网络中使用的节点数、迭代次数、loss值等参数进行相应调整。
(8)重复步骤(3)~(7),直到获得磨齿机热致误差量化方面具有最佳性能的AO-CNN数学模型。
3 热误差实验
3.1 实验过程
选用重庆某磨齿机进行主轴的热态特性实验,采集磨齿机热误差数据。磨齿机主轴系统关键零件的温度通过11个PT100铂电阻传感器测量,以尽可能全面地采集磨齿机主轴温度信息,这些温度传感器主要布置在磨齿机的主轴、大立柱、轴承、床身、托座、油管,具体如图6所示。使用1个非接触电压型涡流传感器MIRAN ML33(误差为±0.25%满量程,精度0.1 μm)用于测量位移,获取主轴X方向热误差数据,如图7所示。

T1—电主轴轴承上;T2—电主轴轴承右;T3—电主轴轴承下;T4—冷却管;T5—大托座;T6—电主轴;T7—电主轴箱体;T8—小托座轴承上;T9—小托座轴承右;T10—大立柱;T11—机床床身。

D1—主轴X方向传感器。
在空载以及进给轴、旋转轴停止不动的条件下对磨齿机进行了测试实验,并且以4组不同的主轴转速对温度数据和热误差数据进行了采集,最大程度地模拟磨齿机在不同转速下的工况,本实验过程中每隔1 s记录一次温度和热误差数据,考虑到温度和热误差短时间内变化缓慢,因此每隔60 s添加标注点,热误差实验转速分布如表1所示。
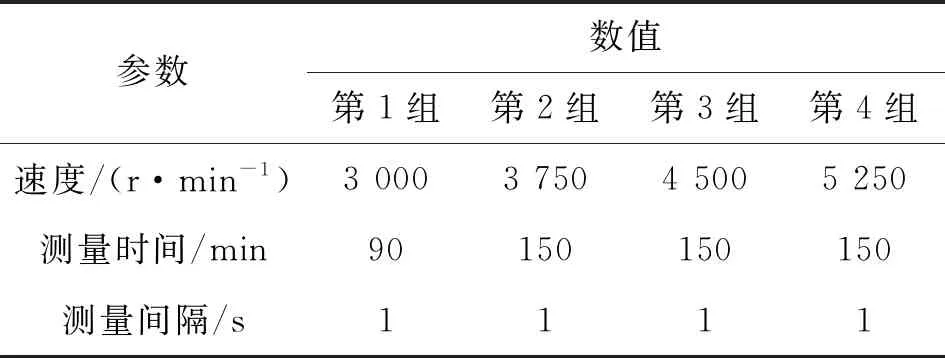
表1 转速分布
3.2 实验结果以及数据分析
3.2.1 温度测试结果
根据机床的运行的时间,4组不同转速下采集到的温度数据变化趋势和样本数量如图8~11所示。

图8 S1=3 000 r/min的温度数据
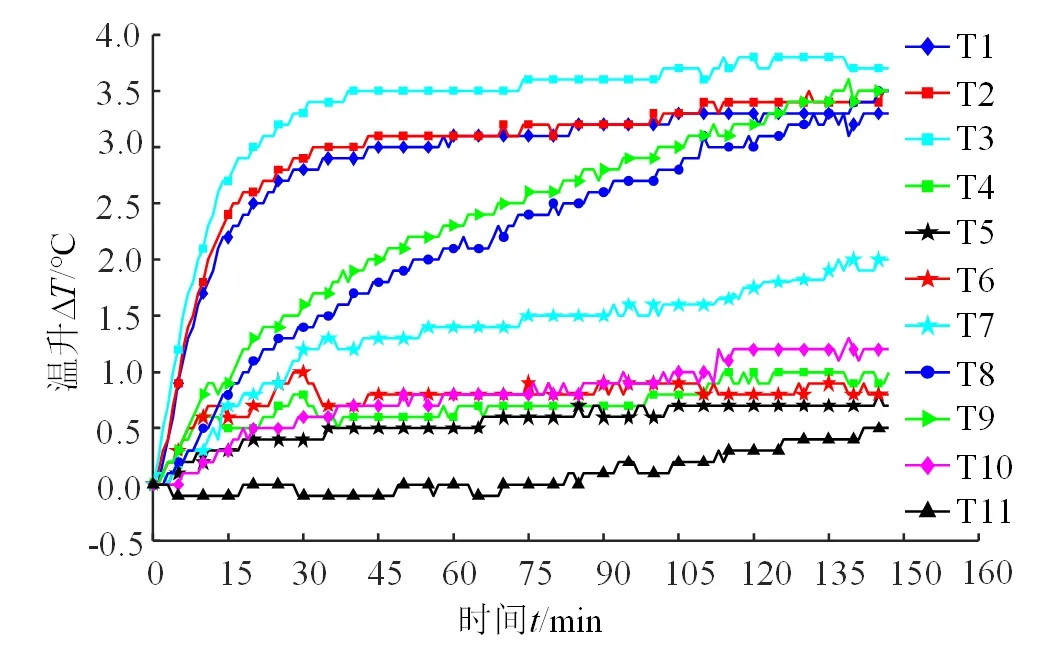
图9 S2=3 750 r/min的温度数据

图10 S3=4 500 r/min的温度数据

图11 S4=5 250 r/min的温度数据
从图中11个温度测点显示出的温升数据可以看出,磨齿机主轴在不同转速下的温度变化趋势大致相同,温度从冷却状态逐步上升,并且,不同部位的温度上升趋势有所不同。其中,与轴承相关的测点温度变化较快,主要原因为轴承处的摩擦会产生大量的热量,使得内部温度升高。并且,随着主轴转速的增加,各个测点的温度变化速度增快。
由于磨齿机主轴系统电主轴端具有冷却系统,而小托座端没有,导致了主轴大小托座温度变化具有明显差异。从4组实验中可以发现,当主轴转速低,如S1=3 000 r/min时,磨齿机电主轴的冷却系统功率较低,产生的大量热量导致T1、T2、T3温度测点温升速率较高。当主轴转速较高时,电主轴冷却系统冷却功率增大,抑制了T1、T2、T3的温升,导致此状态下的T8、T9温度测点温升速率更高。
3.2.2 热误差测试结果
根据设计的实验方案获得4组不同转速下的磨齿机主轴X轴向的热漂移数据,如图12所示。
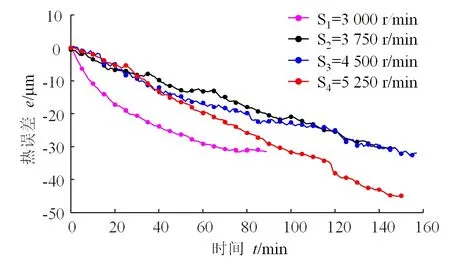
图12 不同转速的主轴热误差数据
根据图12所示,不同转速下的主轴热变形趋势大致相同,在磨齿机主轴运转初期,随着运行时间的增加,主轴的X向热漂移逐渐增大,运行一段时间后变化趋势逐渐放缓。由于磨齿机电主轴配备有冷却系统,当温度变化较小时,磨齿机冷却功率较低,而到达一定温度后,冷却系统功率增大,导致热误差数据的波动,从而磨齿机在S1时的热误差与其他3个转速的热误差相差较大。
4 热误差建模结果与模型性能分析
4.1 关键温度点筛选结果
以主轴转速S1=3 000 r/min、S4=5 250 r/min的实验数据作为训练样本,根据式(3)CH指标得到的最佳聚类数为3,CH指标值计算结果见图13。

图13 最佳聚类数结果
由式(2)、(4)、(5)模糊聚类算法对T1~T11总计11个温度测点进行聚类分析,得到隶属度矩阵

(14)
隶属度矩阵U从上至下的3行代表了3类,从左到右的列代表了11个温度测点T1~T11,温度测点的聚类结果如表2所示。

表2 不同温度测点的聚类结果
由表2可知,模糊C均值聚类将温度测点分类的结果为3。为了筛选出同一类温度测点与热误差数据相关程度最大的点,使用相关系数法计算其相关性,计算结果如表3所示。温度测点的相关程度由大到小的排序为T3>T2>T1>T10>T4>T6>T11>T8>T9>T5>T7。

表3 不同温度测点与热误差的相关度
根据不同温度测点排序结果与表2不同温度测点的聚类结果,筛选出第1类关键温度点为T3,第2类关键温度点为T8,第3类关键温度点T10。使用模糊C均值聚类与相关系数相结合,将温度点从11组降低到3组关键温度点,筛选出磨齿机最具代表性的温度测点,减小计算量的同时便于对后续卷积神经网络建模的开展,提高模型的稳定性以及预测能力。
4.2 AO-CNN建模结果
将筛选出的关键温度点T3、T8、T10数据输入到天鹰优化卷积神经网络中,以主轴转速S1=3 000 r/min和S4=5 250 r/min为训练数据建立基于天鹰优化器的卷积神经网络数控机床主轴热误差预测模型。在卷积神经网络模型中,设置了两层卷积层、两层池化层和两层全连接层,卷积层和池化层的滤波器大小为2×2,学习效率为0.01,最小损失值loss为0.012。激活函数用于去线性化,在本研究中,采用ReLU激活函数。在所有的温度测点中,只有温度变化明显的区域与热误差值有关,因此模型需要提取的特征是有限的。ReLU具有单边抑制的特性,使得网络稀疏激活。因此,可以更好地挖掘热误差的特征,训练数据。ReLU的数学模型可以表示为
H(x)=max(0,x)
(15)
将温度数据和热误差数据进行了归一化处理,输入到AO-CNN模型中进行训练。训练过程中最小损失随迭代数的变化如图14所示。

图14 最小损失值曲线
4.3 基于AO-CNN的热误差模型预测性能分析
为了验证本文所提的AO-CNN热误差建模预测性能与泛化性能,使用遗传优化算法优化的BP神经网络和MLR热误差模型同AO-CNN热误差模型进行对比分析。
将主轴转速分别为S2=3 750 r/min和S3=4 500 r/min时的实验数据作为测试预测精度的数据,输入到AO-CNN热误差预测模型中,并且将该模型与利用同样实验数据的GA-BP神经网络和MLR热误差预测模型进行对比分析。
本文选择的热误差预测准确度评价指标为均方根误差(root mean square error,RMSE),公式为
(16)

不同模型的热误差预测结果如图15、16和表4所示,表中均方根误差1和均方根误差2分别为主轴转速为S2=3 750 r/min和S3=4 500 r/min的RMSE。可以看出,AO-CNN模型的残差曲线整体波动较小,预测曲线与实际热误差曲线的偏差更小。在不同转速下,AO-CNN模型和CNN模型与MLR模型和GA-BP神经网络模型相比具有更好的预测效果,RMSE更小,并且AO-CNN模型相较于CNN模型的平均RMSE减小了15%。由此说明,天鹰优化算法能够提高卷积神经网络模型数控机床热误差的预测效果,在不同工况下维持高预测精度和稳定性。

(a)热误差预测图

(a)热误差预测图

表4 不同模型在不同转速时的RMSE
5 结 论
为了进一步提高热误差建模精度,减少数控机床加工的热误差,本文在对磨齿机主轴热变形和磨齿加工分析的基础上,提出了一种基于天鹰优化算法的卷积神经网络数控机床主轴热误差模型。
首先,采用FCM聚类和相关系数法,以CH指标为评价指标,将温度测点从11个减少至3个。然后,将温度和热误差数据转变为数组的集合,以图片的形式输入CNN模型,并用AO优化了CNN的卷积核大小。最后,在2种不同转速工况下,将AO-CNN模型与CNN模型、BP神经网络和MLR模型对比分析。结果表明,相比于传统的BP神经网络模型和MLR模型,AO-CNN模型具有在不同转速下预测精度高、泛化性强的优点,平均RMSE相比BP神经网络模型、MLR模型和传统CNN模型分别减小了58%、48%和15%。AO-CNN模型为建立数控机床热误差模型和热误差补偿提供了一种可靠的方法。

