新型SRC柱-H型钢梁组合节点有限元分析

乔光德，刘继明，吴成龙，谭文娅，王传贻，张祥威

(青岛理工大学 土木工程学院，青岛 266525)

近年来，国家对预制装配式建筑结构的大力推广，使预制装配式框架结构的抗震研究成为了国内外学者关注的重点，型钢混凝土柱和钢梁作为一种组合结构，由于其良好的抗震性能被广泛应用于装配式建筑结构中梁柱节点的连接。

SALVATORE等[1]通过试验测试发现钢-混凝土复合结构能够合理地利用材料且具有很高的预制能力，可以提供高水平的延展性和耗能能力。DENG等[2]介绍了一种完全预制的梁-柱节点，其中包含复合钢超高性能混凝土，通过试验研究发现节点具有良好的承载力和抗震性能，并为梁柱节点连接提出了理论模型。WU等[3]提出了一种新型的模块化预制复合接头，研究低周往复循环荷载作用下3个不同刚度比试件的失效过程和特性，发现该新型复合接头具有较高的承载能力和良好的抗震性能。芦静夫等[4]利用ABAQUS对新型装配式钢-混组合梁柱节点进行有限元数值模拟，结果发现：该新型节点在多遇地震作用下承载力较好，受力性能优异，且节点连接高效，可提高装配效率。张健新等[5]对工字钢、对拉螺栓和方钢管3种不同连接形式的新型装配式钢混框架中节点进行低周往复荷载试验，发现方钢管连接形式的试件有着最高的累积耗能能力、承载能力和变形能力，且破坏形态最优。张爱林等[6]发现端板式装配式梁柱连接节点可以有效控制翼缘连接板刚度变化，利用翼缘连接板导致的变形去消耗地震能量，从而保证梁柱等主要构件不发生破坏。程万鹏等[7]对预制装配式部分钢骨混凝土框架结构梁柱节点进行试验研究，发现该节点比普通钢筋混凝土节点承载力高2～3倍，且承载力退化速率较慢，在保持高承载力的同时还具有较好的延性。刘震等[8]对预制装配式H型钢骨混凝土柱-柱连接的节点进行有限元受力分析，发现该节点的初始刚度、承载力和延性性能较好，且轴压比和剪跨比对节点的静力性能影响显著。王燕[9]阐述过塑性铰外移的必要性，通过“强柱弱梁，强节点”的设计思想使梁端出现塑性铰，从而形成较大的变形能力和耗能能力。郭子雄等[10]对新型装配式钢筋混凝土柱-钢梁框架节点进行低周反复荷载试验，发现该节点的破坏模式均是梁端出现塑性铰，通过梁绞机制破坏来充分耗能。

目前，预制钢-混凝土复合结构组成梁柱节点的抗震性能方面的研究较少。因此，本文在课题组前期拟静力试验研究的基础上，采用ABAQUS软件对新型SRC柱-H型钢梁组合边节点进行数值模拟，得到的滞回曲线、骨架曲线和破坏形态与试验曲线吻合较好，说明了有限元模型的可行性，进而分析节点盖板长度和柱轴压比2个参数变量对该节点抗震性能的影响。

1 试件概况

1.1 试件设计与制作

新型SRC柱-H型钢梁组合边节点的设计如图1所示，主要由预制的SRC柱、H型钢梁和节点核心区模块3部分组成，试件所用型钢均为Q355B，SRC柱的截面尺寸为350 mm×350 mm，主要由H型钢骨HW150 mm×150 mm×7 mm×10 mm，4根直径20 mm的HRB400级纵筋，直径8 mm的HPB300级箍筋，以及外包C40混凝土组合而成；钢梁尺寸为280 mm×150 mm×10 mm×10 mm；上下柱和节点核心区模块通过M20的S10.9级摩擦型高强螺栓连接；钢梁和节点核心区模块采用同级别的M24摩擦型高强螺栓连接；在施工现场通过栓焊混合连接的方式进行快速装配，在达到装配快捷的同时，也能满足“强柱弱梁”的抗震设计原则。

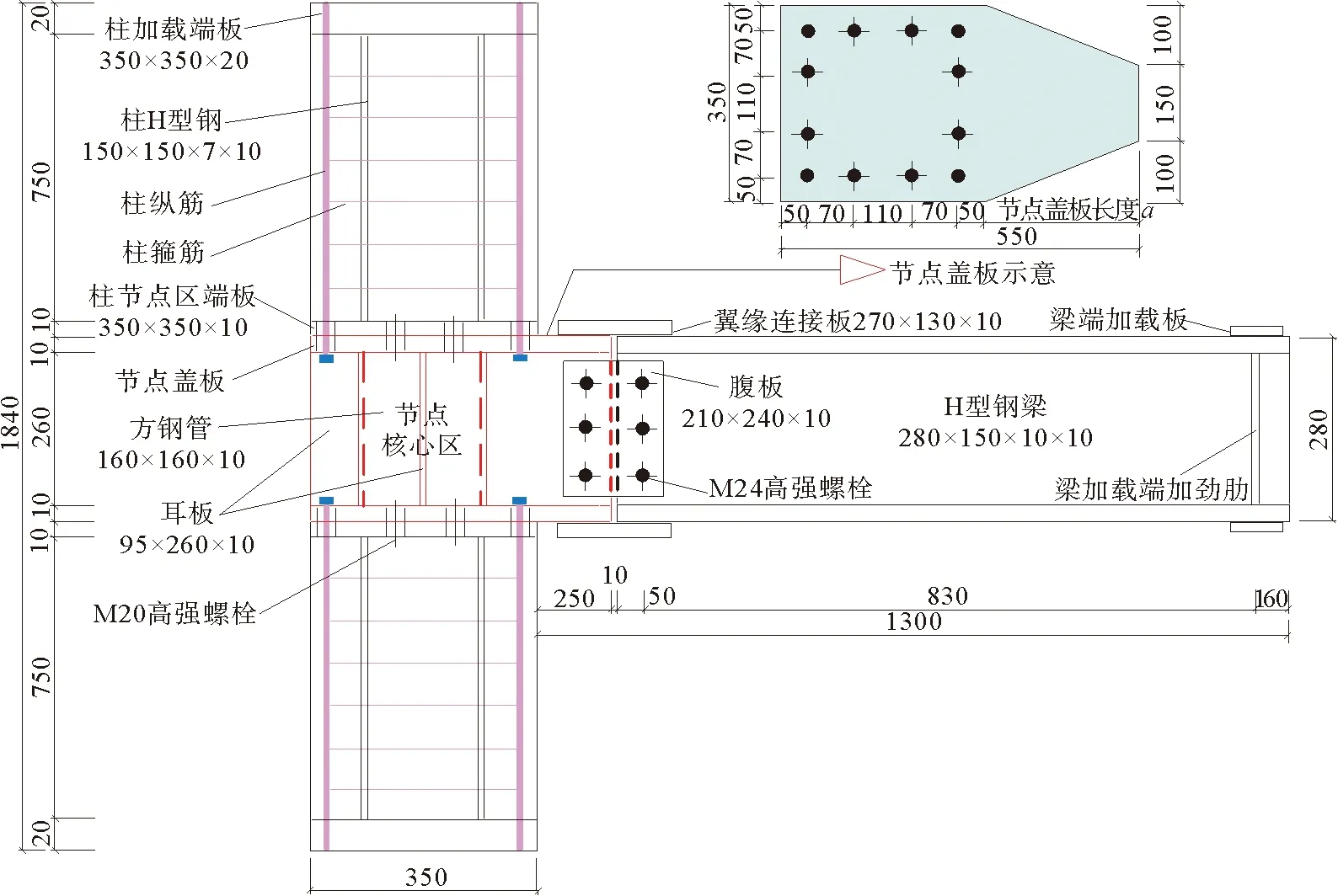
图1 新型SRC柱-H型钢梁组合节点(单位：mm)

1.2 加载装置和加载制度

本次试验依照规程[11]中荷载-位移控制的方法进行加载，试件的屈服荷载根据理论计算确定，屈服之前采用荷载控制，屈服之后位移控制；试件加载至梁端载荷下降为85%的峰值荷载或者试件有明显破坏现象时，停止试验。加载装置和加载制度分别见图2和图3。

图2 试件加载装置

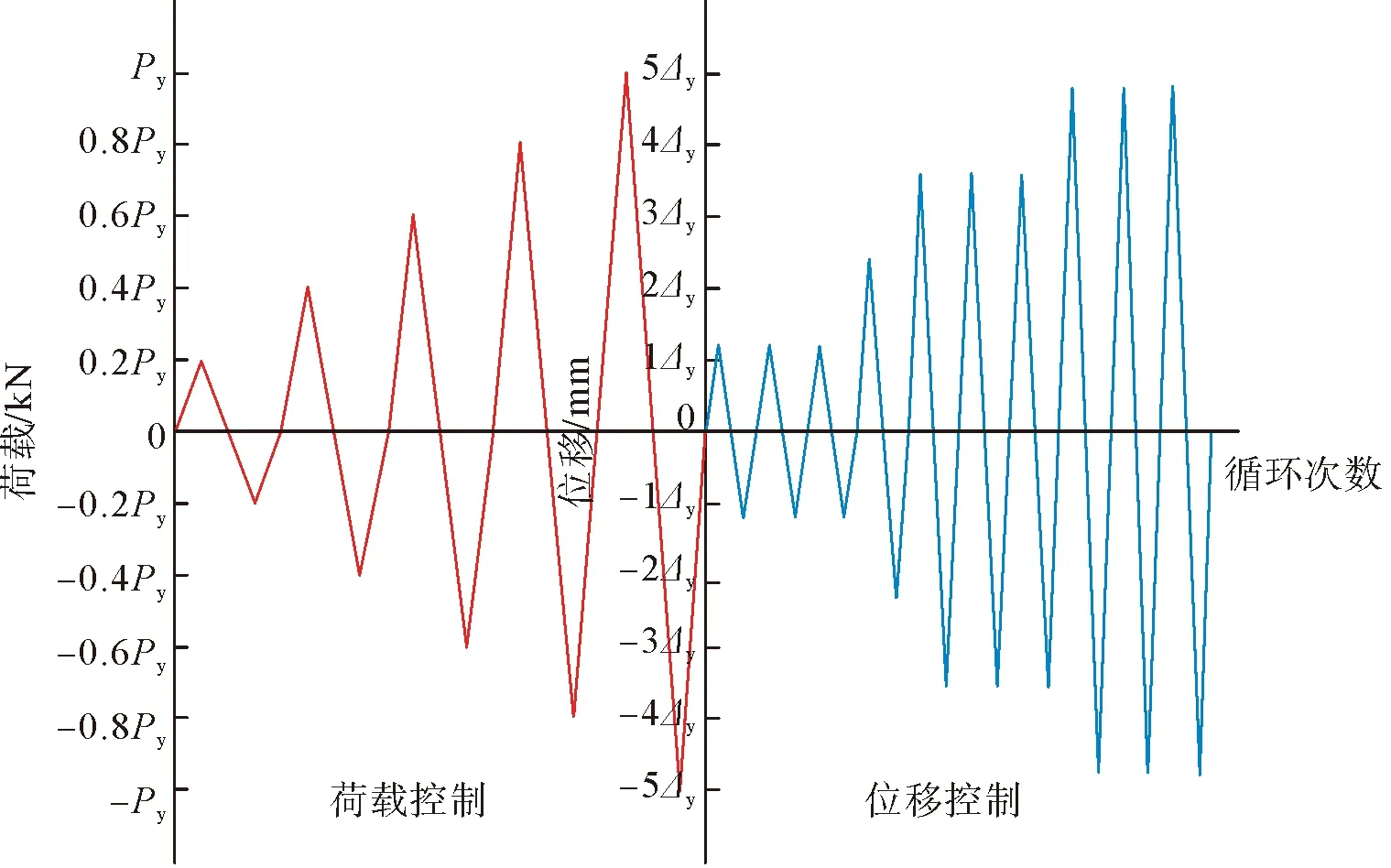
图3 加载制度

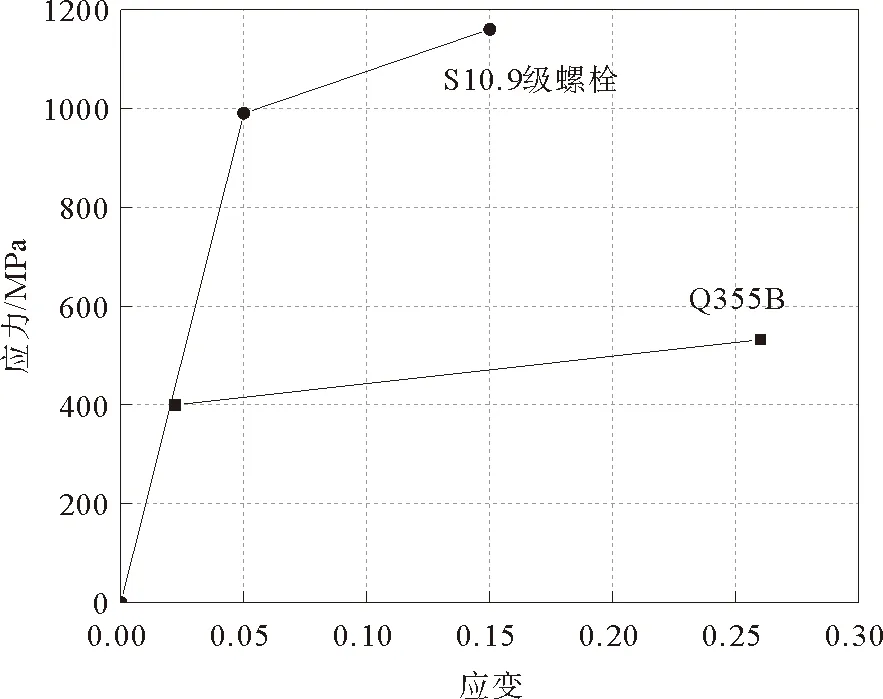
图4 材料本构关系

2 有限元模型建立与验证

2.1 材料本构关系

本文所用的型钢均为Q355B，弹性模量为2.06×105MPa，密度为7.85×103kg/m3，泊松比取为0.3，钢材、螺栓均采用简化处理的二折线本构模型[12]，材料的本构关系见图4。型钢、螺栓和钢筋在计算中均使用Von-Mises屈服准则及相关联的流动法则。混凝土采用塑性损伤模型，其本构关系基于规范[13]建议的应力-应变曲线。

2.2 网格划分及相互作用

本模型中纵筋和箍筋采取T3D2单元进行网格划分，其余部件采用C3D8R单元，以保证求解的精确度。由于试验中试件的变形主要在节点核心区附近，故方钢管、节点盖板、翼缘连接板和腹板等厚度方向至少划分2个网格单元；节点核心区和上下柱及梁之间通过螺栓的预紧力进行连接，M24和M20高强螺栓的预紧力分别是255和155 kN，螺栓网格划分精细；上下柱纵筋外伸至节点核心区的部分采用“等效螺栓”进行替代，等效螺栓的材料属性设置为纵筋的属性，两者之间采用“耦合”的方式进行约束连接；节点盖板和梁翼缘部分通过翼缘连接板进行“绑定”约束来模拟试件中的焊接，螺栓和螺栓孔之间采用“表面-表面”接触，考虑到螺栓和螺栓孔之间存在间隙，为调整区域指定容差设置为1，其余“表面-表面”接触均设为0.1，接触的摩擦系数为0.35，有限元网格划分和边界条件设置见图5。

图5 有限元网格划分和边界条件设置

2.3 边界条件

ABAQUS数值模拟所建立的边界条件要与试验相一致，本模型先在梁端部创建参考点RP1，上柱顶面中心位置为RP2，柱底面中心位置为RP3，通过耦合的方式将这3个需要运动的面进行约束。其中梁端加载端RP1的y位移方向和x，z转角方向进行约束限制；柱顶RP2的x，y位移方向和x，z转角方向进行约束限制；柱底RP3的x，y，z位移方向和x，z转角方向进行约束限制。轴压力所需的集中荷载通过参考点RP2施加在柱顶面的中心位置，模型的低周往复循环荷载加载点设置在梁端参考点RP1，以此来和试验的边界条件相对应。

2.4 有限元模型验证

由图6可见，试验和模拟的破坏形态均是在翼缘连接板处形成塑性铰，受压侧的翼缘连接板屈曲变形，受拉的一侧撕裂变形，两者的破坏模式相近说明了模型的可行性。

图6 破坏形态对比

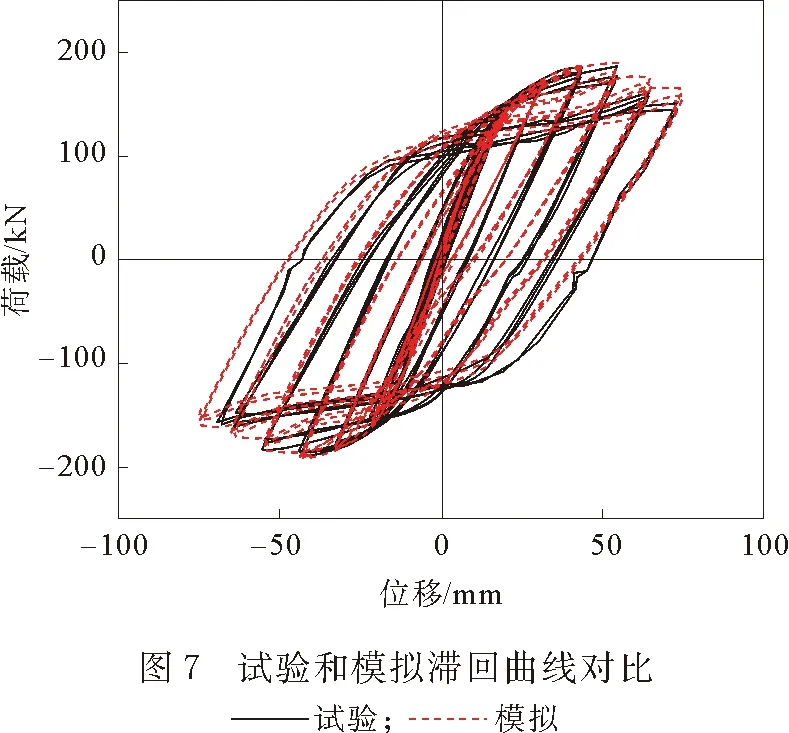
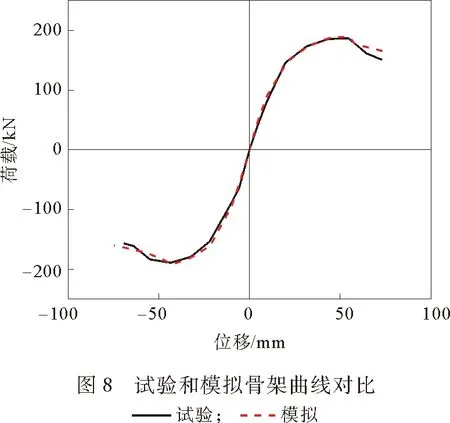
试验和模拟的滞回曲线对比见图7，可见两者结果吻合较好。两者曲线整体较为饱满，呈现梭形，反映出其塑性变形能力较好，具有良好的耗能能力；加载初期，两者都处于弹性阶段，荷载-位移曲线基本成线性增加，随着位移加到25 mm后，滞回曲线包围的面积开始加大，说明试验和模型耗能增加；加载后期，试件的强度、刚度退化较快，模拟时由于材料属性和边界条件设置过于理想化，所以模拟曲线总体上比试验曲线更为平滑和饱满。图8是试验和模拟的骨架曲线对比，可见两者曲线走势基本一致，均有着明显的弹性、强化和破坏3个阶段。滞回曲线和骨架曲线与试验结果相近进一步验证了模型的准确性。

3 有限元参数分析

3.1 节点盖板长度对抗震性能影响

考虑到节点盖板长度(Length of Joint Cover，简称JCL)取值的不同会影响到塑性铰的位置，本文在节点盖板长度a为250 mm的BASE试件基础上模拟了150 mm(JCL-1)、200 mm(JCL-2)、300 mm(JCL-3)和350 mm(JCL-4) 4个长度，进一步探究节点盖板长度对试件抗震性能的影响。

3.1.1 骨架曲线和特征点分析

参数JCL模型的骨架曲线见图9，用“能量等值法”在骨架曲线上求出屈服位移Δy，峰值荷载Pm的85%为破坏荷载Pu，对应位移为破坏位移Δu，平均延性系数μ取试件的破坏位移Δu与屈服位移Δy的比值，各特征点均是取正负向循环的平均值，特征点值汇总于表1。

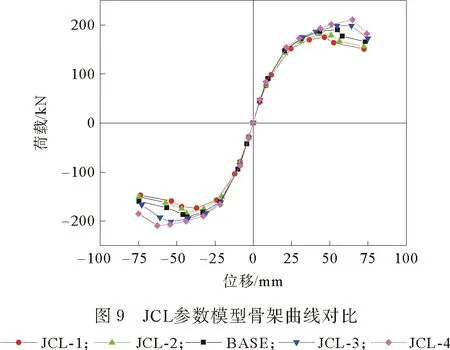
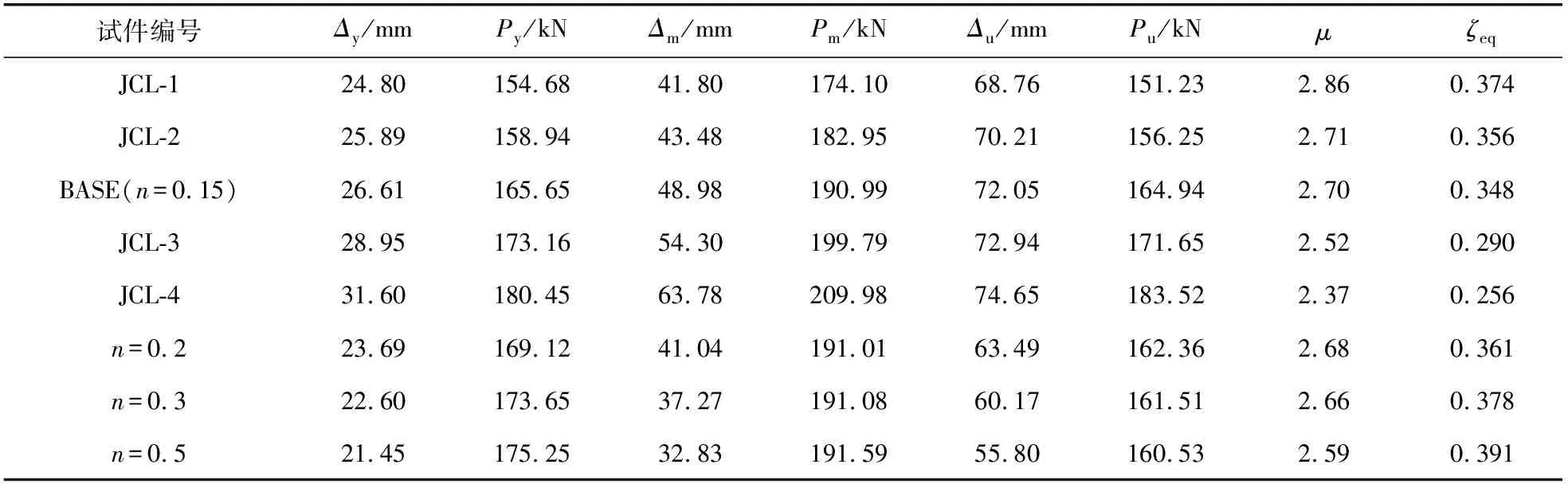
表1 节点模型的特征点值汇总

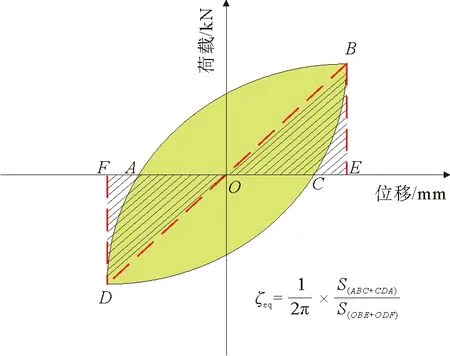
图10 等效黏滞阻尼系数ζeq计算示意

从表1和图9可知，各模型在弹性阶段基本一致，随着节点盖板长度的增加，JCL-4模型相较于JCL-1模型屈服位移和屈服荷载分别增加了27.4%和16.7%，JCL-4模型相较于JCL-1模型峰值位移和峰值荷载分别提高了52.6%和20.6%，JCL-4模型相较于JCL-1模型破坏位移和破坏荷载分别增加了8.6%和21.4%，JCL-4模型相较于JCL-1模型延性减小了17.1%，其主要原因是节点盖板长度增加，相当于塑性铰外移距离加大，塑性铰处的弯矩是恒定的，由V=M/L知，梁加载端距离塑性铰的位置变小，所以梁加载端剪力加大即承载力变大。

本文采用等效黏滞阻尼系数ζeq来表示试件在地震作用下的耗能能力，ζeq计算公式和示意见图10，S(ABC+CDA)为滞回曲线最后一级加载位移，第1循环的包络面积；S(OBE+ODF)为图中△OBE和△ODF的面积总和。由表1可知，等效黏滞阻尼系数随着节点盖板长度的增加而减小，表明试件的耗能能力变差，JCL-1模型相较于BASE模型等效黏滞阻尼系数增加了7.5%，JCL-4模型相比于BASE模型减小了26.4%，节点盖板长度为350 mm时耗能能力下降最为严重。图11为JCL参数模型达到破坏时的型钢应力云图，可见JCL-4模型的节点盖板和柱节点区端板连接处有一定程度的弯曲变形，此时节点核心区应力增大，容易引起节点域的脆性剪切破坏，说明塑性铰位置离节点核心区越远，模型的耗能能力越差。

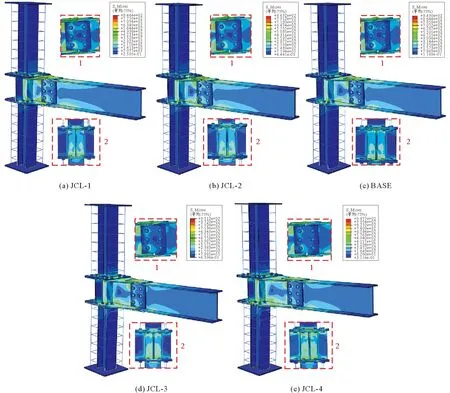
图11 JCL参数模型的型钢应力云图

3.1.2 强度退化和刚度退化

本文采用强度退化系数λj表示强度退化的特性，该特性可描述为节点承载力在相同级别加载条件下因循环次数增多而降低的现象。

(1)

式中：Pj为第j(取j=1)次循环中的峰值荷载；Pmax为整个循环中的峰值荷载。

图12为节点盖板长度对强度退化曲线的影响。从图中可以看出各模型均有着明显的对称性；各模型的强度退化系数在0.6～1.0之间区别较大，其中JCL-1，JCL-2和BASE 3个模型强度退化曲线较为接近，上升段较快，模型屈服较早，达到峰值荷载时的位移较早，峰值荷载后逐步退化；JCL-3，JCL-4模型前期上升段较慢，达到峰值荷载时的位移较晚，峰值荷载后迅速下降；说明节点盖板长度超过250 mm的模型后期强度退化较快。

本文采用环线刚度Kj来描述刚度退化，表示节点刚度随着循环加载次数增多而逐渐变小的特性。

(2)

节点盖板长度对梁端位移-环线刚度曲线影响见图13。由图13可见，环线刚度正负向对称明显；随着位移的增大，各模型刚度退化模式和规律趋于一致，且在加载前期刚度退化较快，加载后期退化速率放缓；节点盖板长度越大的模型初始刚度越大，这是因为翼缘连接板远离节点核心区，塑性铰外移距离加大。

3.2 柱轴压比对抗震性能影响

柱轴压比是影响抗震性能的一个重要因素，试验的柱轴压比n取值为0.15，考虑到实际工程中该比值会偏大，所以本文模拟了3种柱轴压比值，分别为0.2，0.3和0.5，以此来研究柱轴压比对该试件抗震性能的影响。

3.2.1 骨架曲线和特征点分析

不同柱轴压比模拟的骨架曲线见图14。4条骨架曲线在加载前期比较相近，随着位移的增大，骨架曲线走向出现变化，柱轴压比增大会使屈服位移提前，由表1可知，n=0.5模型比BASE模型提前5.16 mm，峰值荷载过后，轴压比较大的骨架曲线下降更快，延性系数有所下降，这是因为轴压比增加时轴力变大，混凝土截面压应力和压应变都增加，致使受压区高度增加，截面的极限变形能力减小，最终导致延性降低，方林等[14]研究型钢混凝土十字形异形柱时也验证了这点；BASE模型相比于n=0.5模型等效黏滞阻尼系数从0.348增加到0.391，提高了12.4%，徐金俊等[15]研究型钢混凝土柱也同样证明了提高轴压比能增加试件的耗能能力，这是因为随着柱轴压比值的增大，模型的屈服位移、峰值位移和破坏位移都会提前，钢材的屈服程度更高，说明柱轴压比的增大能显著提高模型的耗能能力。

3.2.2 强度退化和刚度退化

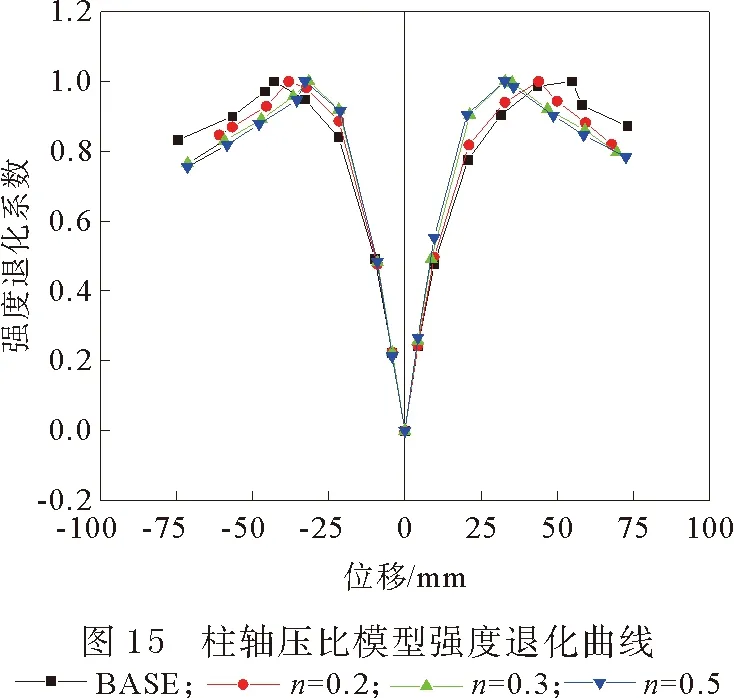
柱轴压比的位移-强度退化系数曲线变化见图15。可见，不同轴压比的强度退化系数均在0.8～1之间区别较大；在加载前期，轴压比较大的模型强度上升较快，屈服较早；各模型到达峰值点后，柱轴压比越大曲线下降越陡峭，说明强度退化越快，模型的破坏也会提前，这也是导致高轴压比延性较低的一个原因。

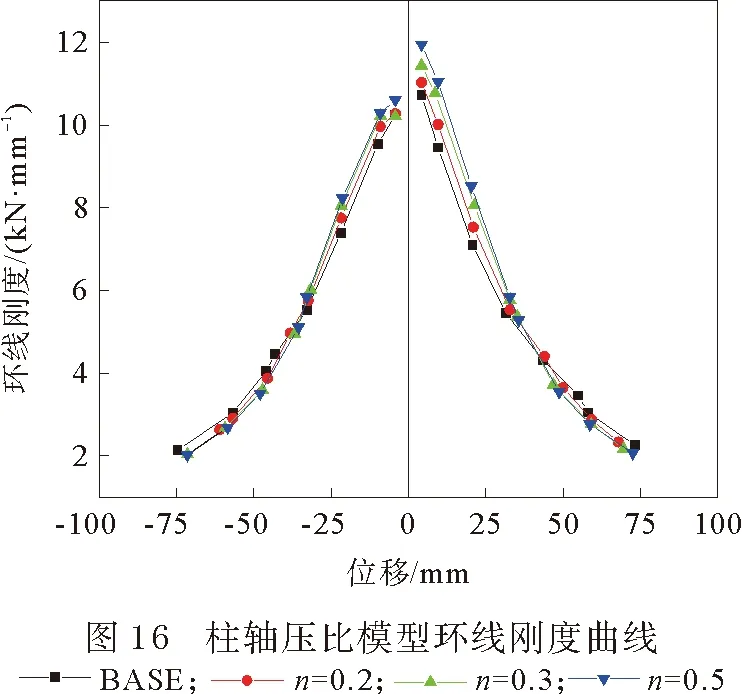
不同柱轴压比下梁端位移和环线刚度曲线变化见图16。轴压比的增大对模型的初始刚度有着明显的提升，这是因为上下混凝土柱和节点核心区之间随着轴向压力的增大而结合得更紧密；各模型环线刚度在加载前期整体呈线性退化，后期退化速率放缓，且加载到峰值荷载后，轴压比越大的模型，退化速率越快。

4 结论

本文在拟静力试验的基础上，通过ABAQUS对节点建立了8个精细化的有限元模型，研究了节点盖板长度和柱轴压比对预制装配式SRC柱-H型钢梁组合边节点抗震性能的影响规律，得出结论如下：

1) 预制装配式SRC柱-H型钢梁组合边节点在低周往复荷载作用下，其破坏位置均发生在翼缘连接板处，实现塑性铰外移的目的，体现“强柱弱梁，强节点弱构件”的抗震设计思想。

2) ABAQUS有限元软件模拟出的结果能够较好地吻合试验结果，说明有限元软件模拟此类节点的抗震性能具有可行性，可为后续深入研究提供理论依据。

3) 节点盖板长度所模拟5个模型的延性系数和等效黏滞阻尼系数平均值为2.63和0.33，体现出模型整体延性性能和耗能能力较好；当节点盖板长度增加时，模型的破坏荷载和峰值荷载都有着显著的提高，表明模型的承载能力得到提高，但模型的耗能能力、延性和滞回性能均有所下降。

4) 轴压比从0.15增大到0.5，模型的屈服位移和破坏位移都会提前，耗能能力和初始刚度提升较为明显，但加载后期强度、刚度退化速率也越快，延性下降较多。