基于人工智能的Lasso-GBDT 信用卡风险评级方法

◎司孟慧 郭威 陈传龙

一、引言与文献综述

信贷市场上存在严重的信息不对称问题，由于借贷双方信息不流通，商业银行等借贷机构难以真正掌控申请用户的全部有用信息。为了有效降低信用卡风险，一方面需要完善用户的个人信息，另一方面需要建立一套完善的信用评级体系，以有效管理信息不对称引发的信用卡风险，克服对用户信用的主观臆断，提升信用卡事前风险识别和事中风险管理能力。许多国家在2008年国际金融危机后相继加强了对金融风险的管控，而信用风险是金融风险的主要部分，因此加强信用风险管理研究成为各国防范系统性金融风险的重要举措（李卫娥，2020）。

当前与信用卡违约风险有关的文献主要集中在两个方面：一是研究信用卡的影响因素。一些学者侧重分析持卡人的个人特征、家庭特征及信用卡消费状况等因素对信用卡违约的影响。如宋红敏、范杰（2015）使用Logistic回归模型分析了信用卡的申请使用是否受性别和年龄、受教育程度、收入、家庭负担和社会保障等因素影响。张晓红等（2017）利用非参数Kruskal Wallis检验方法研究了性别、年龄、受教育程度和收入等因素对信用卡使用情况的影响。吴锟、吴卫星（2018）基于Probit模型和IV Probit模型在控制户主年龄、学历、家庭净财富、收入、住房等变量后，分析了金融素养对使用信用卡的影响，得出金融素养水平同居民家庭使用信用卡成正相关的结论。惠锐、郭华世（2019）通过建立VAR模型，分析了主要宏观经济指标对我国商业银行信用风险的影响。

二是研究信用卡违约的影响因素以及对违约风险的评估或预测。在信用卡违约的影响因素方面，Li et al.（2019）使用COX比例风险模型，研究了中国信用卡用户的多样性、独立性和社会因素对信用卡违约的影响，发现信用卡违约与信用卡用户收入的多少无关，而与收入的稳定性显著相关。刘阳、张雨涵（2020）采用Probit模型在控制户主特征变量、家庭特征变量及宏观经济变量后，研究了居民金融素养水平对信用卡违约的影响。在对信用卡违约风险进行评估或预测方面，葛君（2010）利用因子分析方法选取了变量，使用Logistic回归方法对信用卡违约风险进行了预测。方匡南等（2010）采用基尼法判断重要变量，使用随机森林方法建立了信用卡违约风险预测模型，并与Logistic方法、支持向量机、分类回归树进行比较，结果发现随机森林方法的预测准确率较高。方匡南等（2014）引入了能够进行变量选择和参数估计的Lasso-logistic降维方法建立了信用卡违约风险预测模型，在比较其他logistic方法后发现Lasso-logistic方法预测精度较高。刘铭等（2017）在考虑变量实际意义和相关性分析的基础上选取指标，分别基于改进的神经网络、传统神经网络、支持向量机和分类决策树法建立了信用卡用户违约预测模型，比较后发现改进的神经网络法准确率较高。

综上所述，要对信用卡违约风险进行准确预测，重要的是选取具有高关联度的变量去构建科学准确的信用评级指标体系，并选择有效的方法建立预测模型。构建有效的信用评级指标体系，关键是要识别出核心变量。建立预测模型则要注重模型外推预测效果，选用模型时充分考虑到模型之间的互补性，尝试采用构建组合模型对信用卡违约风险进行预测。本文主要贡献在于：第一，构建基于互补性的Lasso-GBDT组合式信用评级模型，并测算出高准确率的客户违约结果；第二，引入具有惩罚项的Ridge Regression、Lasso Regression和Elastic net Regression方法对变量进行筛选，既可以解决多重共线性的过度拟合问题，又可以减轻算法计算难度（上述方法具有筛选变量的功能）。

二、模型理论及构建

本文构建能够进行变量筛选和信用风险预测的组合模型，引入带有惩罚项的Ridge Regression、Lasso Regression和Elastic net Regression三个模型实现变量初步筛选，并在此基础上构建GBDT信用评级模型。

（一）构建筛选变量模型

因变量个人信用卡是二元离散变量，需要首先构建logistic线性回归表达式。假设有独立同分布的观测值（xi，yi），i=1,2,3…,n，其中xi=(xi1,…xip)和yi分别是解释变量和被解释变量。则logistic线性回归方程的条件概率为：

式子（4）和（5）通过引入不同的惩罚项（L1和L2范数正则化）实现对影响信用卡违约率的变量进行筛选，以剔除不必要的变量。前者通过惩罚项实现系数压缩，系数不会压缩到0（Tibshirani R et al.，2004）；后者能够在回归系数的绝对值之和小于常数的约束条件下最小化残差平方和，从而使得某些变量的系数为0。式子（6）中，当2=0时，Elastic net Regression方法即为Ridge Regression方法；当2=1时，Elastic net Regression方法即为Lasso Regression方法。Elastic net回归方法的2介于0和1之间。

（二）建立GBDT 信用评级模型

在上一步基础之上构建的GBDT模型具有适合低维数据、调参时间短、预测率高等特点。GBDT由Friedman（2001）首先提出，是一种基于梯度提升集成决策树的非线性模型，用损失函数负梯度来拟合本轮损失近似值。即通过梯度提升让每一次迭代都在减少残差方向建立一个决策树，以增加预测精确性。在GBDT迭代中，假设前一轮得到的强学习器是fm-1(X)，损失函数是L(y,fm-1(X))，此轮迭代目标就是找到一个弱学习器hm(X)，使得损失函数即L(y,fm(x))=L(y,fm-1(X)+hm(X)）最小。GBDT的分类损失函数为：

如果达到迭代次数或误差达到阈值，即返回fM(x)，然后得出预测概率值，并根据概率阈值将其归到相应的类别。通过以上迭代过程，即使用二元类别预测概率值和真实概率值的差来拟合损失，不断地接近真实的信用卡违约概率值，达到准确预测个人信用卡违约的目的。

三、特征描述及预处理

（一）变量描述

本文数据来源于2020年我国某大型商业银行的信用卡部，共有39923笔信用卡信贷数据，数据中的客户违约有7218笔，而非违约有1957笔。由于文章缺失数据比例较低，因而将缺失值与异常值所在行进行删除。教育程度和学位两个变量数据缺失严重，将以上两列数据予以删除。解释变量中包含性别二元离散数据变量及多个连续型数据变量，考虑到不同连续型数值变量单位各有不同，本文对所有数值变量进行均值中心化和方差规模化等标准化处理，使得模型参数估计系数具有可比性。具体特征如表1所示。

表1 变量说明

表2 Elastic Net Regression 模型RMSE 值

（二）指标体系初步确定

选择合适的信用评级指标体系是建模的基础。由于存在的冗余变量并不能帮助我们有效预测信用风险，反而测算结果可能由于变量间的自相关性等影响模型效果。选取合适的解释变量作为信用评级指标体系有助于银行体系信用卡发卡银行的审核和重点监控。为了识别对因变量有用的特征、提升模型预测准确率，本文首先对所选用的39个特征变量运用Frank（1993）的Ridge Regression、Tibshirani（1996）的Lasso Regression和Hui&Hastie（2005）提出的Elastic Net Regression模型三种方法进行特征选择，即调用R软件分别对式子（4）、（5）和（6）进行参数估计。

图1 三种模型下的系数路径图

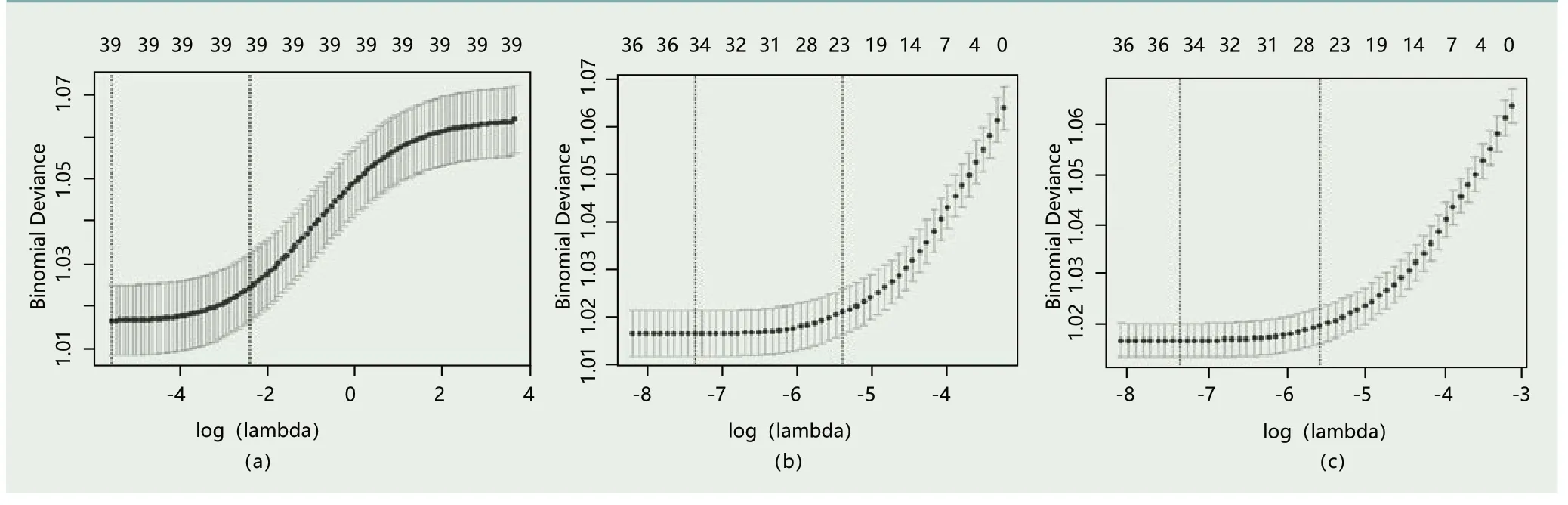
图2 三种模型下的交叉验证结果图

变量筛选模型中，三个模型控制高相关性数据的惩罚参数α取值有所不同，Ridge Regression和Lasso Regression模型α值固定为0和1，而Elastic Net Regression模型α值介于0和1之间。因此，为更好地选取Elastic Net Regression模型，我们通过对比0.1～0.9这9个不同α值下的RMSE，RMSE值越小，则模型的预测能力越强。通过选取最小的RMSE值所对应的α值可以确定Elastic Net Regression模型，具体的测算结果如表2所示。

通过表2的结果可知，当α值为0.9时，Elastic Net Regression模型的RMSE值最小，为80.98122。我们选择的Elastic Net Regression模型惩罚参数α取值为0.9。本文将使用惩罚参数各为0、1和0.9的Ridge Regression、Lasso Regression和Elastic Net Regression三种模型对数据进行变量筛选，其系数路径和交叉验证结果分别如图1、图2所示。

图1-(a)、图1-(b)和图1-(c) 纵坐标是所选择变量的系数值，分别为Ridge Regression模型、Lasso Regression模型和Elastic Net Regression模型的选择路径图，随着横坐标λ值的不断增大，其对系数的压缩程度越大，模型筛选掉的变量就越多，因而图1中3个子图上侧的变量数目也越来越少。从三个模型的系数路径图可知，39个特征变量被选择留在模型中的数目越来越少，特征变量按照重要性程度依次被选择到模型中，最先进入模型中的变量具有较强的预测能力，表示其违约概率估计的影响越大。

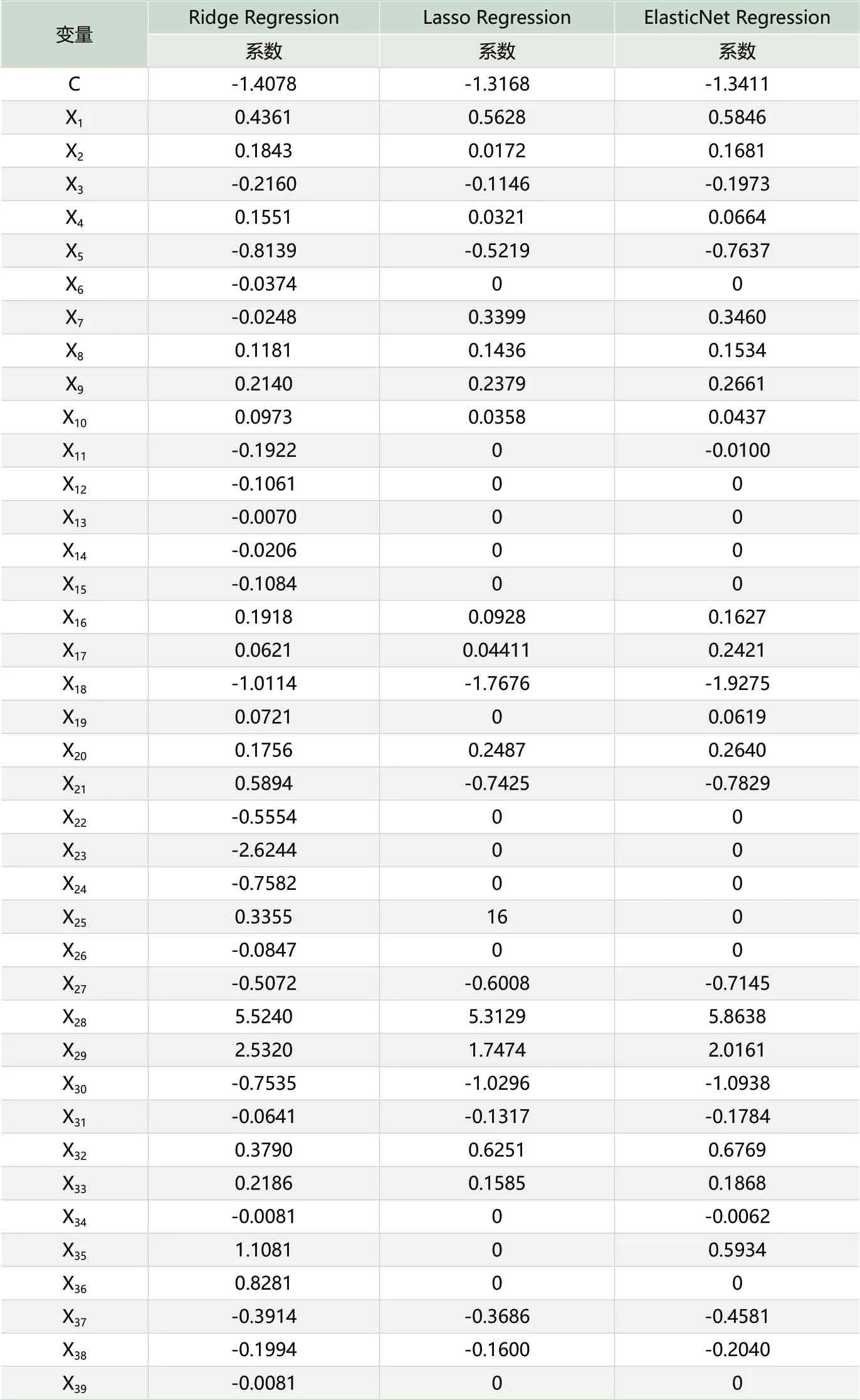
表3 变量选择和参数估计结果

本文采用交叉验证的方法选择最为适合的参数λ，以提高模型的稳健性。Ridge Regression、Lasso Regression和Elastic Net Regression模 型的交叉验证结果如图2-(a)、图2-(b)和图2-(c)所示，与图1三个子图一一对应，图2三个子图中横坐标为λ取值，纵坐标为交叉验证的误差平方和。图2中三个子图都有两条垂直虚线，左侧虚线为lambda.min，是给出最小平均交叉验证误差的λ值，右侧虚线为是lambda.1se，该虚线与横坐标交叉的λ值给出了模型，使得误差在最小值的一个标准误差以内，同时也是一个方差范围内得到最简单模型的那一个λ值。Tibshirani（1996）认为，λ估计值在左右两侧虚线区间内模型预测偏差变动幅度相对较小，一般建议选取使模型相对简洁的λ值。我们利用广义交叉验证直接选择使模型误差较小且相对简洁的λ值，即lambda.lse所对应的λ值。根据R运行结果，Ridge Regression模型、Lasso Regression模型和Elastic Net Regression模型选取的λ值分别为0.0905、0.0045和0.0038，图2三个子图中lambda.lse值从左至右依次为lnλ1=-2.4025、lnλ2=-5.4028和lnλ3=-5.5766。此时R语言运行结果显示，Ridge Regression模型并未删除任何特征变量，选取的变量数目为39个，而Lasso Regression模型将16个冗余变量进行删除，筛选出的变量为23个，Elastic Net模型的变量筛选数目介于以上两模型中间，为27个变量。以上三种模型在实现变量筛选的同时，也对变量系数进行了测算，为了更便于三种模型之间的横向对比，现将三种模型的初步变量筛选结果进行系数估计，如表3所示。

由结果可知，信用卡信用违约概率中具有重要解释作用的特征变量均被列入模型中。变量X28、X23、X29、X35和X18在Ridge Regression模型中是影响信用卡违约概率测算的重要变量，而在Lasso Regression模型中， 变 量X28、X18、X29、X30和X21是影响信用卡信用风险的五个 重 要 变 量，X18、X21、X28、X29、X30等5 个 变 量 对Elastic Net Regression模型来说较为重要。可以看出变量X28对三个模型的影响最为重要。接下来，基于三个模型变量筛选的结果来测算三个模型的RMSE值，该值越小则说明模型的预测能力越强，对比结果如表4所示。

Lasso Regression模型的均方根误差最小，因此在接下来的建模过程中，我们将使用该模型筛选出的特征变量进行测算。

表4 三种模型预测能力对比

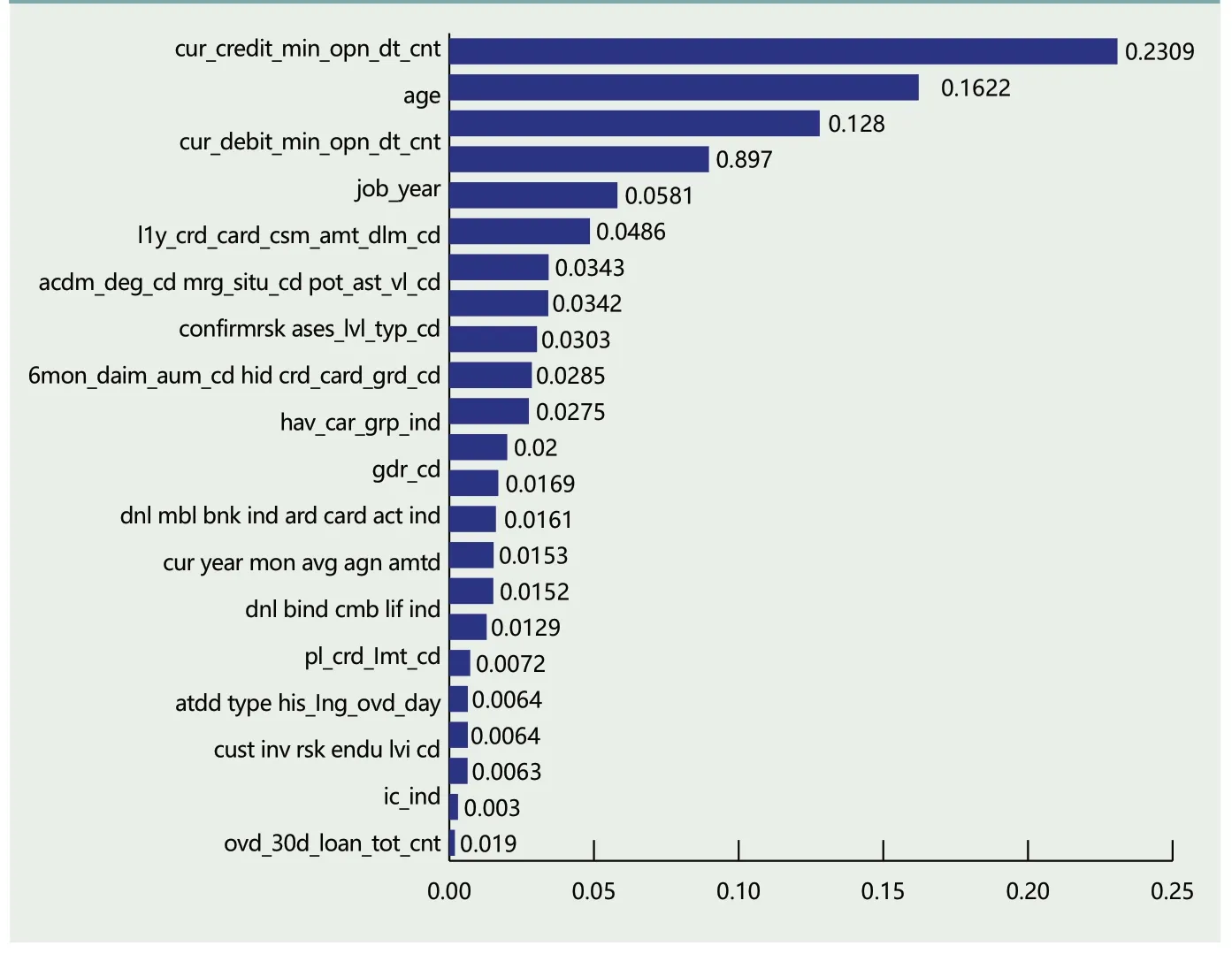
图3 RF变量重要度排序

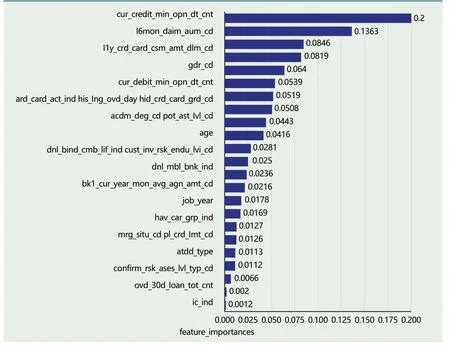
图4 GBDT变量重要程度排序

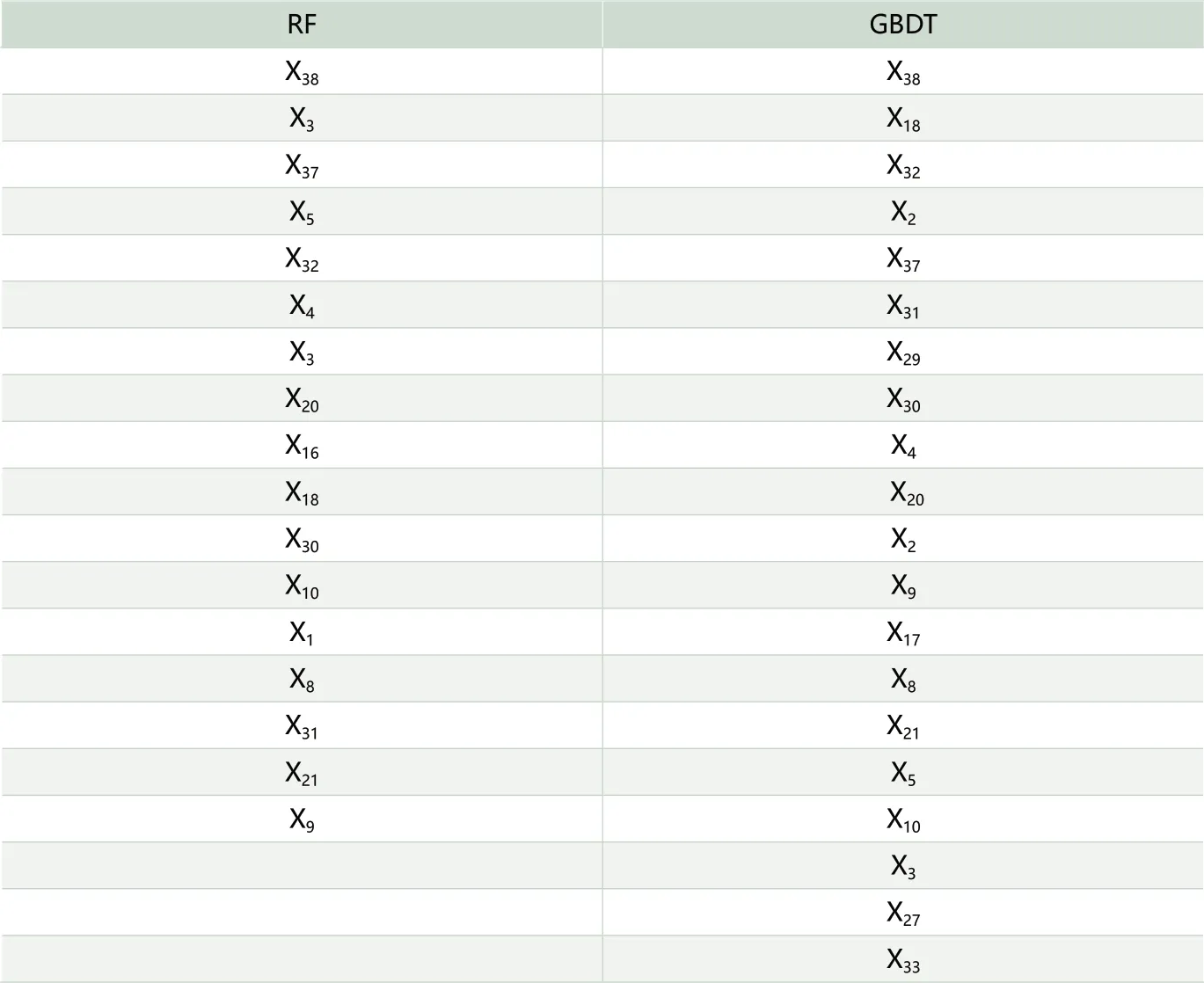
表5 模型组合的指标体系

表6 准确率和AUC 测算结果

四、实证分析

（一）评级指标体系的确立

在信用卡信用评级模型确定之前，有必要选择合适的信用评级指标体系。上文中Lasso Regression模型已经筛选出与因变量相关的23个特征变量，为进一步对比变量重要性，利用构建的GBDT模型对23个特征变量的重要性进行排序和分析，使用RF模型作为对比，变量排序结果如图3和图4所示。

通过对比图3和图4的结果，可知23个特征变量在RF和GBDT两个模型变量选择结果中存在差异。持有信用卡天数对两个模型来说是最重要的特征变量，年龄在RF模型中的重要程度排名第二，而在GBDT模型中却并不是特别重要的特征变量，从用户是否有工商标识在两个模型测算结果的排名中可以看出，该特征变量对用户违约率影响程度不大。婚姻状况在RF中对信用卡评级的影响较大；但在GBDT模型中，该特征变量却对信用违约率影响较小，该模型的研究结果与Chen et al.（2009）的研究结果一致。而两个模型对学历的研究结果与Din&Kleimeie（2007）在越南学历和信用风险的关系研究结果存在差异，本文构建RF和GBDT模型的结果显示学历对信用违约率存在一定影响，而Din&Kleimeie（2007）则认为学历对信用违约率并没有显著性影响。为了找出重要变量，缩减无关变量是统计分析中的常规做法。为了更好对比RF与GBDT两个模型违约率准确度，我们将选择对模型重要程度超过0.01的特征变量分别进行模型测算，两组模型变量确定的指标体系如表5所示。

（二）模型结果与解释

RF以17个重要特征变量作为输入变量建立信用评级模型，GBDT将输入前20个特征变量建立信用评级模型。当前我们的总体数据具有不平衡性，测算前需要对数据进行随机过采样处理。为了验证模型的准确率预测能力，将样本数据集划分为训练和测试集，训练集用于建模，测试集用于验证模型测算准确率。将训练和测试集分别划分为9：1、8：2、7：3、6：4和5：5以确定最优划分比例。构建一个分类器，需要选择评价标准对分类器的性能进行评估（李艳霞等，2019）。选择常规的准确率评价标准对分类模型性能进行评估，表6为Lasso-RF和Lasso-GBDT组合模型的准确率和AUC测算结果。

从表6的结果可以看出，Lasso-RF组合模型在训练和测试集划分比例分别为9：1、8：2、7：3、6：4和5：5的预测结果中，训练集AUC预测都超过了99%，比例为9：1的测试集预测结果在三者中最高，AUC值为66.3%。Lasso-GBDT组合模型中，比例为9：1的测试集预测的AUC值最高。Lasso-RF和Lasso-GBDT两组模型在训练和测试集划分比例为9：1的测试集预测结果最优。从表6的结果可以看出，RF的训练和测试集预测结果差距超过20%，Lasso-GBDT的训练和测试集预测结果差距虽然小于Lasso-RF模型，但也存在一定差距。考虑到RF和GBDT模型会存在过度拟合问题，接下来对两组模型预测结果最优的9：1训练和测试集划分比例进行调参处理。

调参方式为随机、网格和贝叶斯调参。为使泛化误差达到最低点以获得最优预测准确率，决定分别使用这三种调参方式对比例为9：1的数据进行调参，通过对比来选取最优调参结果。随机、网格和贝叶斯调参结果如表7和图5所示。

表7 调参后准确率结果

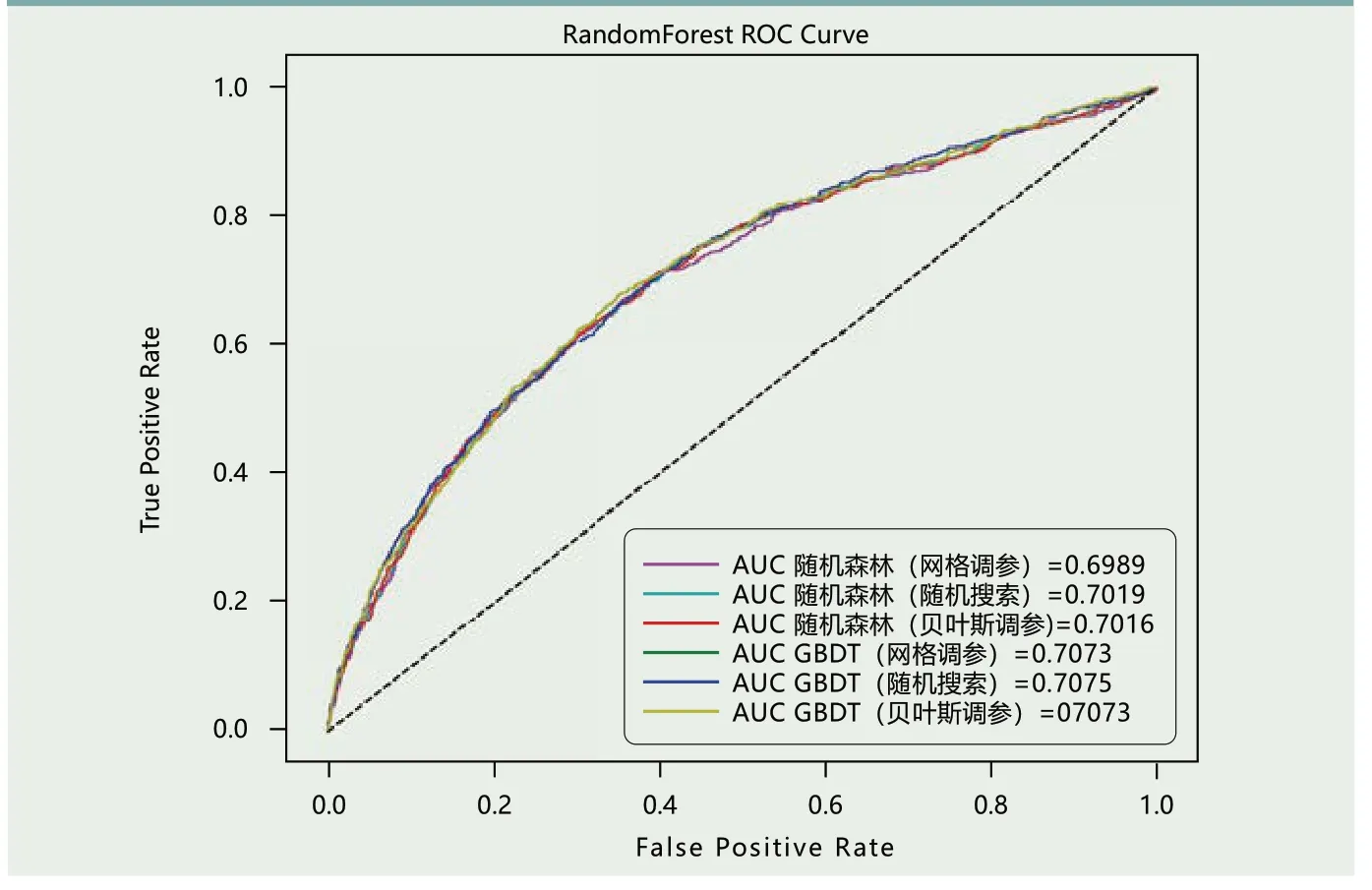
图5 调参后AUC结果

由结果可知，两组模型调参后缩小了训练和测试集的准确率测算结果差距，RF模型随机调参结果最为理想，随机调参后AUC结果最高，为70.19%。经随机调参后GBDT预测结果最理想，模型预测的训练和测试集差距最小，调参后AUC值为70.75%。调参后GBDT模型AUC结果都高于RF模型，说明GBDT模型在信用卡违约率测算中预测准确度高于RF模型。

在信用评估中，银行等金融机构最关注的是用户的违约预测准确率，即把违约用户预测为非违约用户的概率，原因在于如果将违约客用户预测成非违约用户，会提高用户违约风险率，将带来巨大经济损失。因而有必要将用户违约率细分为违约预测与非违约预测准确率，表8为根据GBDT模型预测得到的分类准确率表格，显示了该模型对用户违约和非违约准确率的预测。

3049个信用卡用户中，被GBDT模型正确判断的有2099个，被错判的有995个，预测准确率为67.84%；859个信用卡违约用户中，551个用户被正确判断，308个被错判为非违约用户，准确率为64.14%；GBDT模型总预测准确率为67.04%，总体看该模型预测效果良好。

表8 违约准确率与非违约准确率

五、结论与政策建议

（一）结论

当前市场存在信息不对称问题，因而抵押贷款可通过抵押品实现信息传递，但是在没有抵押的信用卡市场中，金融机构只能依靠充分利用用户历史信息、挖掘用户违约特征等人工智能方式提高信用风险管理水平，提升对违约用户的识别能力（王正位等，2020）。学者们希望研究的信用评估模型能够给贷款机构带来最大的期望利润，或者带来最小的错误分类成本。为提升信用卡用户违约准确率，基于分析单一模型的基础上，引入信用评级组合模型对样本数据进行测算。使用Lasso Regression模型对样本数据进行变量筛选，有效剔除与因变量Y不相关的自变量，有效避免建模过程中无关变量特征对模型效果的影响。

本文构建了基于互补性的Lasso-GBDT组合模型，实证研究表明该组合模型比Lasso-RF组合模型更具准确性。通过实证分析得出以下结论：一方面，相较于单个模型，组合模型数据测算中能够充分利用每个模型的优点，并且有效避免单个模型数据测算存在的弊端，提高数据测算的准确率。另一方面，通过Lasso-GBDT信用评级模型可知，持有信用卡天数、工资、信用卡消费金额的层级、性别和借记卡天数、历史贷款最长逾期天数是最具影响力的变量，而人们普遍关注的婚姻和年龄变量却很少带来信用卡的违约风险，与方匡南等（2010）、赖辉（2017）的结论不太一致，他们认为婚姻状况和年龄是影响用户信用卡违约的关键因素。

（二）政策建议

本文基于国际先进评级机构的成熟经验，从银行和政府两方面对如何完善我国信用评级体系提出政策建议。

1.完善信用评级系统。（1）完善基础数据库。基于实证结果可知，完善的用户数据积累是金融机构进行信用评级的重要基础。基础数据库包括事前数据和事后数据，事前数据是信用评级前收集整理的用户基础数据，用以防范信息不对称问题；而事后数据是对信用评级结果统计分析后的数据库。商业银行等金融机构应完善包括事前数据和事后数据在内的信用评级基础数据库。（2）建立信用评级跟踪监测体系。信用评级体系并非一蹴而就，而是一项需要持续更新并不断优化的长期工作，需要在评级的整个过程实行动态监控和静态监控相结合的全程监控模式，以保证信用评级体系有效运行。（3）建立专业队伍。建立一套科学系统的信用评级体系需要一支具备专业素质和具备一定分析与判断能力的人才队伍作为重要支撑。金融机构应加强对信用评级人员的培训。一方面，与穆迪等国外先进评级机构合作，定期派人员外出学习国外先进经验；另一方面，聘请国外专家对我国的信用评级进行指导，以保证人员知识体系持续更新。

2.人民银行、银保监会等金融监管机构应为信用卡的健康发展创造良好的市场环境。基于信用评级机构的社会性和国内信用评级业发展现状，我国有必要建立健全金融监管机构体系，以实现对该行业的管理。一方面，监管机构应该对银行等信用评级实行资格认定制度，增强信用风险监管力。另一方面，建立健全信用评级法律法规。2004年颁布的《新巴塞尔资本协议》明确了信用评级的重要性，我国应在该协议的基础上建立信用评级法律，加强对于银行信用评级本身业务经营的法律法规建设，为我国信用评级创造良好的市场环境。