名义代价期望目标下的智能车辆困境避险规划

张荣珅 王玉田 胡荣权 杨灵芳 黄 智

1.湖南大学机械与运载工程学院，长沙，410009 2.湖南大学土木工程学院，长沙，410009

0 引言

智能车辆的使用提高了道路交通安全性。由于技术制约和不可控因素，绝对安全的智能驾驶难以实现。当智能车辆(本文特指具有自主避障能力的智能车辆)无法保障全部交通参与者的安全时，将不可避免地陷入两难困境。由于各种原因(如行人的突然出现或车辆制动故障等)，车辆无法同时避免对本车道及对向车道交通参与者的冲突，由此陷入两难选择：减速避障与本车道交通参与者发生碰撞，或为减小伤亡而转向减速与对向车道交通参与者发生碰撞。

对于冲突不可避免的困境，有研究对避险规划中所涉及的因素人为设定优先级，以获得最优的避险规划。RASEKHIPOUR等[1]、WANG等[2]依据障碍物的可穿越性和碰撞伤害程度对障碍物进行分级排序，其中人类被赋予最高优先级。LUETGE[3]也提出人类在所有障碍物中必须具有最高优先级。CASTRO等[4]、TUMOVA等[5]对驶入人行道、对向车道等违反交通规则的驾驶行为进行优先级排序。裴晓飞等[6]对转向、直行制动等操作划分优先级，避险时选择优先级最高的操作。然而，基于优先级的方法对于受伤害的各方均涉及人的困境难以给出合理避险规划。

两难困境下的避险决策涉及社会伦理问题，伦理原则为解决困境下的避险决策提供依据。多数研究者认为智能车辆避险决策应遵守道义论和后果论[7-9]。THORNTON等[7]认为后果论和道义论是最有效、最切实际的两难困境避险决策理论，并将后果论和道义论映射为两难工况下避险决策的代价和约束条件，力求符合道义论前提且最小后果的避险决策。LIM等[10]强调智能车辆的避险决策应该与社会伦理价值观、法规相结合。后果论追求最小冲突代价，道义论强调对规则的遵守，伦理原则本身具有一定的复杂性并且难以用意义明确的数学模型描述。另外，对规则的绝对服从是不现实的，而违背规则的代价也难以量化，因此给两难困境下应用伦理原则解决避险决策问题带来困难。

相对于道义论，后果论便于量化，研究者更倾向于通过获得冲突中的代价损失，选择最小代价的避险决策[11-15]。RASEKHIPOUR等[12]提出根据碰撞相对速度、相对角度、相对质量等建立代价模型。考虑冲突的不确定性，张东亚[13]以碰撞概率和伤亡概率的乘积为代价模型。KUMFER等[14]通过实验得出在特定的碰撞场景中，尽管其他伦理体系有助于建立机器学习开发所需要的规则，但后果论具有减少事故中人员伤亡的优点。PUGNETTI等[15]依据两难困境中行人的年龄、性别、社会地位等性质得到的生命价值代价进行避险决策。上述研究在计算代价损失时，忽略了道义对代价的影响。无差别地计算处于道路不同位置(如行车道和人行道)的人的伤害代价，显然有悖于公众的伦理价值观。

综上所述，现有研究工作未能有效解决冲突各方均涉及人的伤害的两难困境的避险决策问题，对符合公众伦理价值的冲突伤害代价的量化建模及规划问题优化求解是解决两难工况避险决策的关键。

本文以两难困境下智能车辆避险规划为研究对象，考虑碰撞伤害程度、法规、伦理和冲突不确定等因素，建立冲突各方中对人的伤害名义代价模型，以量化对人的代价损失。以名义代价为优化目标，车辆物理系统限制为约束条件，构建分层避险轨迹规划优化问题。设计了几种典型的两难困境场景，对提出方法的有效性及可行性进行仿真验证。

1 名义代价模型

尽管困境场景复杂多样，但交通参与者可分为三类：本车乘员(U1)、当前车道的道路使用者(U2)、非当前车道的道路使用者(U3)。为便于表述，研究以图1所示仅涉及U2和U3伤害的困境场景为例进行探讨，由于两难困境发生在极短时间内，忽略U2和U3的运动。不失一般性，研究所提出的方法同样适用于伤害涉及U1、U2和U3的复杂困境。

图1 一种典型的两难困境

1.1 名义代价定义

困境冲突中，涉及对人、动物及财产的侵害。基于人的生命至上原则，在涉及对人伤害的冲突中，忽略动物及财产的损失代价，仅考虑对人伤害造成的代价。

名义代价为量纲一参数，描述伤害的相对大小，不仅由生命健康损失所决定，还取决于法律、伦理道德等多个因素。采用名义代价可避免对人生命健康物化造成的伦理争议。

1.2 名义代价的敏感因素

冲突中对人的伤害是名义代价的主要构成。伤亡人数及伤害程度是确定对人伤害代价的关键因素。尽管现实中人的性别、年龄、社会地位、亲属关系等均会影响伤害代价的量化，但对人的区分对待易引起伦理争议，因此上述因素在名义代价建模时被忽略。

困境中避险决策的实质是在各交通参与者间进行风险分配。以图1工况为例，直行制动避险行为使U2承受碰撞风险，转向制动避险行为则通过违反规则(如逆向行驶)将风险从U2转移至U3而获得较小的社会总人员伤害。公众普遍存在两个共识：①将风险转移至无辜的第三方是不道德的行为；②道路使用者应该承担意外的风险，自动驾驶应当挽救更多人的生命。同时，违反规则总会给智能车辆的使用者(或所有者)带来额外的法律风险和道德压力，即使违反规则可能会降低总的人员伤害。因此，上述伦理、法律因素应在量化对U2和U3伤害的名义代价时体现。

1.3 名义代价期望模型

如前述，名义代价不是简单地将对人造成的伤害量化，还受到法规、伦理等因素的影响，伦理实验是获取名义代价的途径之一。本课题组前期开展了伦理实验研究，通过在线问卷调查形式，获得受调查者以智能车辆用户的角度，在面对各种两难困境时的伦理倾向，建立了转向避险倾向IES模型[16](以图1仅涉及U2和U3伤亡的工况为例)：

(1)

式中，N2和D2分别为直行避险造成U2伤害的伤亡数量和伤害程度；N3和D3分别为转向避险造成U3伤害的伤亡数量和伤害程度；其余为模型拟合参数。

问卷调查表假设直行时仅造成对U2的伤害，转向时仅造成对U3的伤害。式(1)中分子部分表示直行避险和转向避险间的伤害代价之差。显然，当直行避险的代价大于转向避险的代价时，公众倾向转向避险，且代价差越大，转向倾向性越强烈。

由于传感误差、动态环境的不确定性，确定性模型难以准确描述避险行为造成的人员伤害。考虑冲突不确定，并基于式(1)IES模型的研究结论，第i条避险轨迹的名义代价期望为

(2)

1.4 伤亡人数期望

伤亡人数期望与人车冲突概率有关，即

(3)

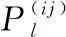
由于Uj方每个人位置不同，故对于同一避险轨迹，车辆与Uj中每个人的冲突概率也不同。

车辆与行人之间的相对距离是判断二者是否发生碰撞的依据[17]。如图2所示，dla、dfp、Δθ分别为人车曼哈顿距离、欧氏距离以及相对方位角。OXY和oxy分别为大地坐标系和车辆坐标系。车辆用一个长L、宽W、航向角为φ的矩形框表示，行人用半径rp的圆表示。仅考虑前碰撞，车头用半径为rv、圆心位于前轴中心的圆表示。

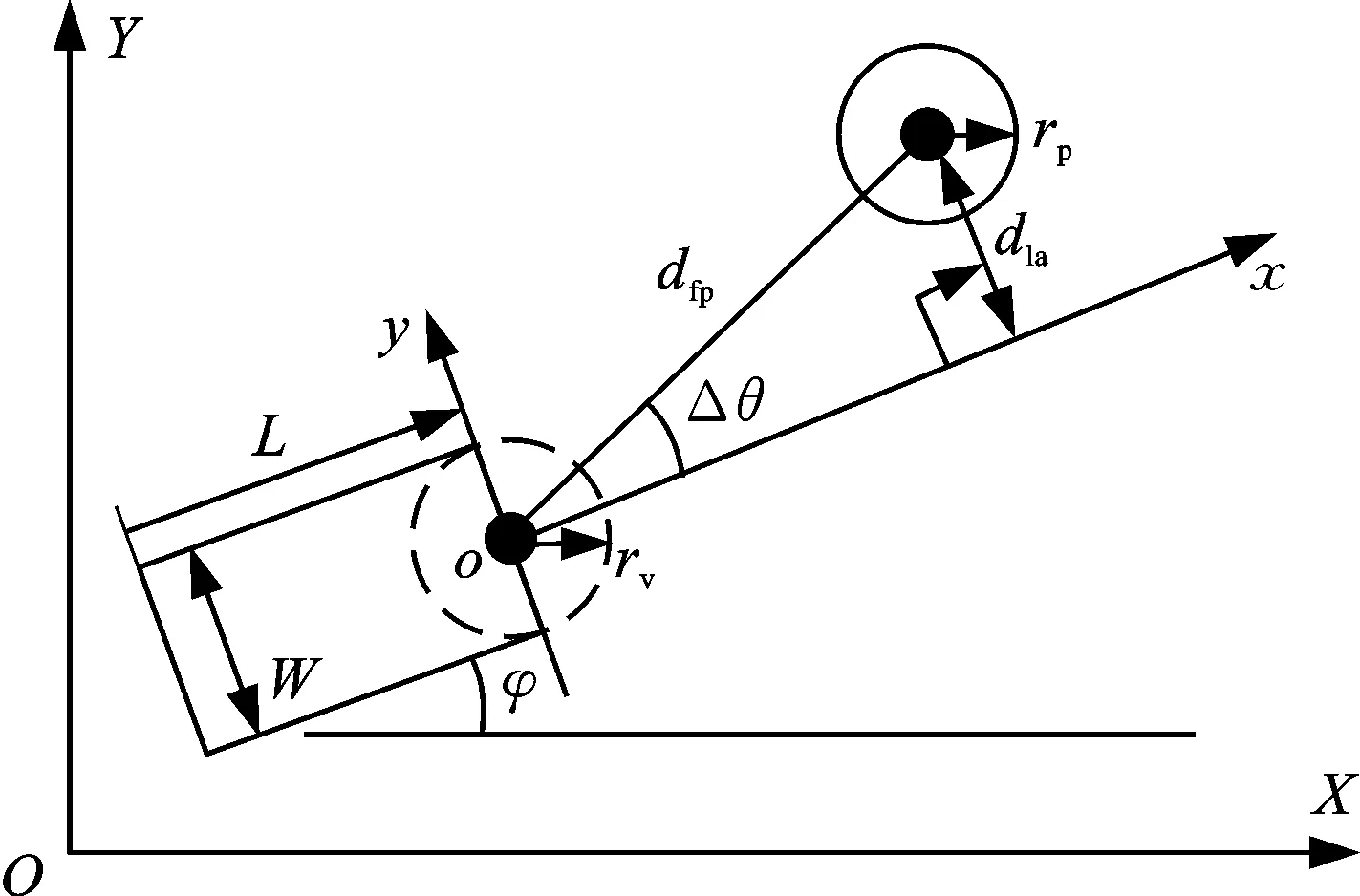
图2 人车碰撞模型简化图

采用曼哈顿距离(即车辆y轴横向距离)描述人车冲突概率：

Pc=1/[1+exp(kc(dla-(rp+rv)-ds))]

(4)

式中，kc为拟合参数；ds为人车间的安全距离，用于描述人车定位误差。

1.5 伤亡程度期望

KONG等[18]通过分析2003—2009年中国真实人车碰撞案例，得到伤亡概率与碰撞速度vc的逻辑回归模型：

(5)

式(5)中PAIS3+(vc)和Pfatal(vc)为碰撞速度vc下行人的重伤和死亡的概率，伤亡程度AIS3以下为轻伤，AIS3+为重伤，fatal为死亡。依据式(5)可以得出碰撞速度vc下行人轻伤概率Pm(vc)、重伤概率Ps(vc)和死亡概率Pd(vc)分别为

(6)

依据AIS的创伤严重度评分法[19]，轻伤、重伤、死亡分别评分为 1、3、6 。碰撞速度vc下行人伤亡程度量化值为

s(v7)=1×Pm(vc)+3×Ps(vc)+6×Pd(vc)

(7)

Uj伤亡程度期望用人群平均伤亡程度表示：

(8)

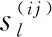
2 两难困境下避险轨迹规划

两难困境中，轨迹规划不能获得无冲突的避险轨迹。以名义代价期望为目标函数，车辆物理系统限制和道路边界等为约束条件，建立避险轨迹优化问题，以期获得最小冲突名义代价且满足车辆动力学、车辆稳定性及道路限制的最优轨迹。

2.1 车辆动力学模型

车辆动力学系统具有高度非线性，考虑模型精度和计算代价，研究采用小角度转向假设下基于线性轮胎模型的单轨车辆动力学模型[20]，如图3所示。

图3 单轨车辆模型

得到动力学方程：

(9)

式中，X、Y和φ分别为全局坐标系下车辆质心位置和航向角；vx、vy和ω分别为车辆质心的纵向速度、横向速度和角速度；m为车辆质量；Iz为车身绕z轴的转动惯量；lf、lr分别为车辆质心到前后轴的距离；FxT为前后轮纵向合力；Fyf、Fyr为前、后轮侧向力；Cf、Cr分别为车辆前、后轮胎的侧偏刚度；af、ar为前后轮侧偏角；δ为车辆前轮转角。

取状态量x=(X，Y，φ，vx，vy，ω)T，控制量u=(FxT，δ)T，即式(9)可表示为

(10)

使用采样时间为Δt的一阶差商方法对式(10)进行离散化得

xk+1=Akxk+Bkuk

(11)

Ak=I+ΔtAtBk=ΔtBt

2.2 车辆物理系统限制

2.2.1控制量约束

约束条件如下：

(12)

式中，FxT，max为地面提供的最大纵向力;δmax为最大前轮转角;Δδmax为前轮转角变化率Δδ的最大值。

这里仅考虑制动避险，故纵向力取负值。

2.2.2轮胎附着力约束

考虑轮胎附着力约束，将前后轴轮胎的横、纵向力限制在摩擦圆中：

(13)

(14)

α∈{f，r}

式中，Fyα，max为忽略荷载转移时的前后轴轮胎最大侧向力；μ为地面附着系数；G为重力。

2.3 道路边界约束

由于道路边界外环境的复杂性及难以预测性，这里仅讨论在道路内的避险规划。采用图4所示的对车辆前后轴中心限制的道路边界约束：

图4 道路边界限制

(15)

α∈{f，r}

式中，Yu、Yl为道路上、下界的Y向坐标值；rf、rr为车前后轴轮廓圆半径；bf，k、br，k为第k个时刻前后轴中心的Y向坐标值；Yk为第k个时刻质心的横向坐标值。

2.4 轨迹规划问题的建立及求解

2.4.1轨迹规划问题的建立

智能车辆避险轨迹规划的优化问题描述如下：

(16)

s.t.k=1，2，…，N

xk=f(xk-1，uk-1)

(17)

E(xk，uk-1)≤1

(18)

bα，k∈lane，α∈{f，r}

(19)

x0=x(t)

(20)

xk∈Xtuk-1∈Utκk≤κmax

(21)

式(17)为车辆动力学离散模型；式(18)为轮胎摩擦圆约束，如式(13)所示；式(19)为道路边界约束，如式(15)所示；式(20)为状态量的初始值约束，其中x(t)为t时刻的车辆状态量；式(21)为状态量、控制量以及轨迹曲率的边界约束，其中Xt、Ut、κmax为状态量、控制量以及轨迹曲率的边界值。

2.4.2轨迹规划问题求解

2.4.2.1 分层优化框架

式(16)所述的轨迹规划问题具有非线性和非凸性。为实现高效求解并避免陷入局部最优，采用分层优化算法[21-22](如图5所示)：上层为“暖启动”层，采用曲线插值的方法[23]在可行域中搜索一条名义代价期望次优轨迹作为下层优化迭代的初始值；下层为数值优化层，采用非线性优化方法在上层给出的初始参考轨迹附近迭代优化，得到满足约束的最优轨迹。

图5 分层优化框架

2.4.2.2 暖启动层

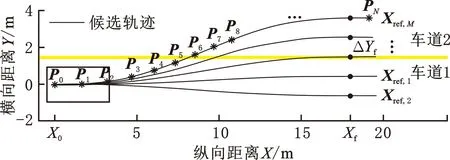
图6 暖启动候选轨迹

2.4.2.3 数值优化层

由于暖启动参考轨迹未考虑车辆物理系统限制，需以其为初始值，在连续空间内进一步迭代寻优。对于式(16)所示的优化问题，采用基于序列二次规划(sequential quadratic programming，SQP)求解器的非线性模型预测控制算法(nonlinear model predictive control，NLMPC)进行优化求解，得到满足名义代价期望最低且符合车辆动力学、车辆物理约束的最优轨迹X*。

3 实验仿真

3.1 实验参数

文献[16]根据对公众的伦理调查结果，对IES模型参数进行了拟合，冲突概率模型参数根据经验选取，如表1所示。轨迹规划算法及车辆主要参数如表2所示。

表1 名义代价与冲突概率模型参数

3.2 实验场景

设计了3个涉及U2和U3伤害的冲突场景，场景信息如表3所示。假设车辆初始检测到两难困境时，位于当前车道中心线上纵向距离1.434 m处，以60 km/h速度行驶，道路附着系数为0.7。

表3 仿真场景参数

3.3 轨迹规划实验结果与分析

3.3.1实验结果

3个困境场景的直行制动轨迹、暖启动参考轨迹、优化后的最优轨迹如图7所示。车辆纵向力规划、速度响应如图8所示。前轮转角规划如图9所示。优化轨迹的车辆前后轮轮胎附着力摩擦圆如图10所示。三个困境场景的直行制动轨迹(Xbra)、暖启动参考轨迹(Xwarm)、优化轨迹(Xopt)对应的对U2、U3方造成的伤亡人数期望、伤亡程度期望以及名义代价期望见表4～表6。

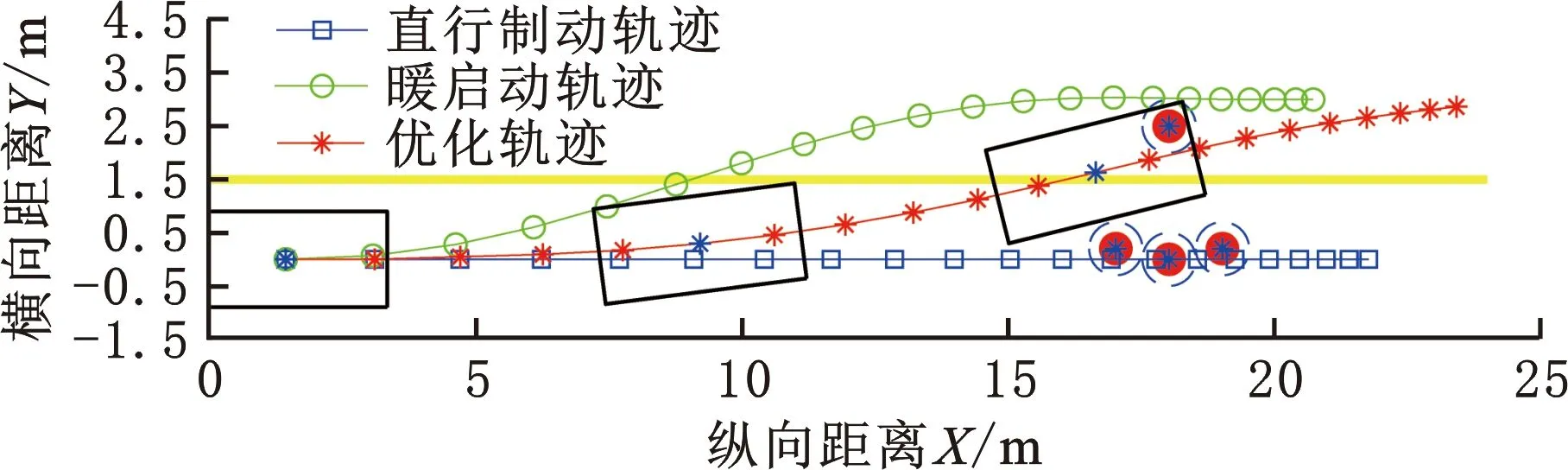
(a)场景1

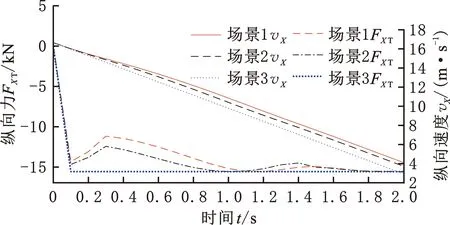
图8 车辆纵向力与速度变化曲线图

图9 车辆前轮转角变化曲线图

(a)场景1前轮摩擦圆 (b)场景1后轮摩擦圆

表4 场景1伤害与名义代价期望

表5 场景2伤害与名义代价期望

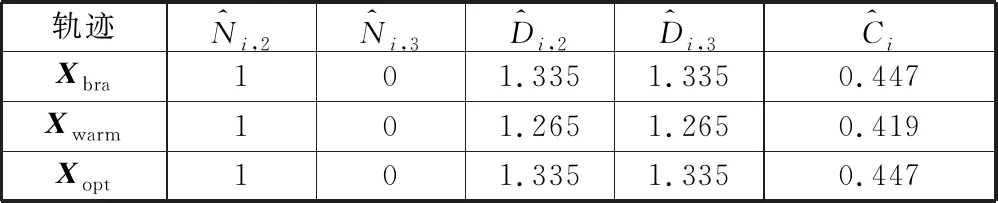
表6 场景3伤害与名义代价期望

3.3.2试验结果分析

由图7和表4～表6可知，场景1中最优轨迹为制动并转向进入对向车道，与U3方碰撞。与直行制动轨迹相比，虽然对U2、U3方的伤亡程度期望都有所增加，但对U2方的伤亡人数期望由3降至0.074，对U3方的伤亡人数期望由0增至0.999，最终使得名义代价期望由1.106下降到0.857。在实践中及伦理调查中发现，若违反规则可以显著降低总的社会伤害代价时，公众倾向于违反规则将风险进行转移至U3。

场景2中，最优避险轨迹选择违反规则越过道路实线，使得对U2的伤亡人数期望显著降低(由2降至0.486)，而对U3的伤害风险略微增加(伤亡人数期望由0增至0.272)，总的名义代价期望大幅降低(由直行制动的0.783减小至0.480)。优化的避险轨迹基本符合公众的显著降低社会总伤害的预期。

场景3中，U2、U3方行人数量相同，转向避险仅将风险由U2转移到U3方，不会产生伤亡程度期望和伤亡人数期望的显著下降，智能车辆的用户反而会因为转移风险至所谓“无辜”的第三方(即U3)而承担法律风险和道德压力。最优避险轨迹选择以最大减速度直线行使，通过降低冲突速度以降低对人的伤害。

对比表4～表6，尽管场景1～3暖启动参考轨迹产生最小名义代价期望，但暖启动轨迹未考虑车辆物理系统限制，轨迹无法跟踪。优化后的避险轨迹的名义代价期望则是系统状态可达条件下的最小名义代价。由图10可知，3个场景下优化轨迹的前轮胎纵横向附着力始终位于轮胎的附着极限，充分利用了轮胎附着力实现转向和减速。

4 结论

(1)针对冲突各方均涉及人员伤害的两难困境，综合碰撞伤亡代价、法规、伦理和冲突不确定等因素，建立避险轨迹对冲突各方的名义代价期望模型，以量化对道路参与者的代价损失。

(2)基于所提出的名义代价期望模型，建立了困境下避险轨迹规划的优化问题。以名义代价期望为目标，车辆物理系统限制、道路边界等为约束条件，采用分层优化算法，解决了两难困境中最优避险轨迹的规划问题。

(3)由3个涉及U2和U3伤害的两难困境场景仿真实验表明，所提出的方法获得的优化避险轨迹符合伦理实验调查时的公众预期。

(4)尽管本文仅讨论了伤害涉及U2和U3方，提出的方法不失一般性，可满足伤害同时涉及U1、U2和U3方的一般困境场景的避险规划要求。