多参数加权p-Laplacian奇异Lane-Emden系统

赵 雪，姜晓威，高 丹，王立波

(北华大学数学与统计学院，吉林 吉林 132013)

0 引 言

Lane-Emden系统的研究源于物理学家和天文学家对气体动力学、传热学以及天体物理学的探索，通过对Lane-Emden系统解的存在性的研究可间接获得行星内部的信息及其他相关物理量.对Lane-Emden系统的研究无论是在理论上还是在应用上都具有非常重要的价值.自20世纪90年代，MITIDERI[1]、SERRIN和ZOU[2-3]，VAN DER VORSTT[4]等学者对Lane-Emden系统的临界曲线进行了系统研究.2002年，BUSCA等[5]研究了Lane-Emden系统

的Liouville型定理，其中p、q>0.对临界曲线下方Lane-Emden系统正解不存在性的猜想给出了部分回答.2016年，QUASS等[6]研究了分数阶Lane-Emden系统

的Liouville型定理，其中α∈(0，1)，N>2α，p、q>0.

受上述文献的启发，本文利用单调迭代技巧研究一类具有p-Laplace算子及奇异非线性项的非线性多参数加权Lane-Emden系统

(Pλμ)

(H)a≥0，0≤f、g≤1，x∈Ω，且在Ω上的一个非零测度子集上f、g>0.

本文的结构如下：第1节主要研究Lane-Emden系统临界曲线的估计；第2节主要研究Lane-Emden系统解的序和参数的序之间的关系.值得一提的是，对于给定的问题，我们只需要半对上下解(而不是一对上下解)就可以得到存在性结果，这显然是一个较弱的假设条件.

1 临界曲线

本节讨论将正象限分成两个连通分支的临界曲线的存在性及其上下界估计.

首先给出一些相关的定义及引理.

引理1[7]设F(x，u)：Ω×→关于x可测，关于u单调不减.设u1、u2∈W1，p(Ω)在空间W-1，p′(Ω)上满足

-Δpu1(x)+F(x，u1(x))≤-Δpu2(x)+F(x，u2(x))，

其中p′=p/(p-1).则当u1≤u2，x∈∂Ω时，有u1≤u2，x∈Ω.

由文献[7]可知，p-Laplacian特征值问题

(Eλ)

具有如下性质：

引理2[7](ⅰ)问题(Eλ)的第一特征值λ1是正的单重特征值；

(ⅲ) 当λ>λ1时，问题(Eλ)不存在正解；

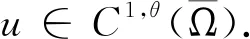
引理3假设条件(H)成立，λ、μ为正参数.若(U，V)是 Lane-Emden系统(Pλμ)的古典上解，则Lane-Emden系统(Pλμ)至少存在一对正解(u，v)，使得u≤U，v≤V.进一步，Lane-Emden系统(Pλμ)存在最小的正解(u*，v*)，使得u*≤U，v*≤V.

证明：设u0=U，v0=V.定义迭代序列(un，vn)如下：

易见(un，vn)是定义好的.由定义1和引理1，可得

0

0

从而存在(u，v)，使得un(x)→u(x)和vn(x)→v(x)，x∈Ω.再由基本的紧性讨论可知，在W1，p(Ω)内，un→u且vn→v.因此，(u，v)是系统(Pλμ)的解.再由引理2知，u、v>0，x∈Ω.证毕.

定义集合

下面我们分别证明集合Λ是非空的、连通的且有界的.

引理4假设条件(H)成立，则Λ非空.

证明：选取0<ρ

定义

，

(1)

由函数h的定义知，(φ，φ)是(Pλ*λ*)的上解.从而由引理3可知，系统(Pλ*λ*)存在正解，即(λ*，λ*)∈Λ.证毕.

由引理3和上下解方法，我们可以很容易地得到如下引理.

引理5假设条件(H)成立.如果(λ，μ)∈Λ，则(0，λ]×(0，μ]⊂Λ.

引理6假设条件(H)成立，则集合Λ有界.

证明：设λ*为特征值问题

(Pλ)

的第一特征值，φ*是相应的特征函数且在Ω上φ*>0.

从而u是问题(Pλ′)的正的上解.另一方面，φ*是(Pλ′)的正的下解.由上下解方法可知，问题(Pλ′)存在解w，使得φ*≤w≤u.这与引理2(ⅱ)矛盾.即问题(Pλ′λ′)不存在正解.再由引理4可知，集合Λ有界.证毕.

证明：对于每个s>0，我们考虑线段

由引理4和引理5，对于每个固定的s，曲线Ls(λ)是非空有界的.

定义

对于任意的(λ1，μ1)，(λ2，μ2)∈O1，设k*=min{λ1，λ2，μ1，μ2}.由引理4可知，(k*，k*)∈O1，我们可以在O1中分别建立从(k*，k*)到(λ1，μ1)和从(k*，k*)到(λ2，μ2)的两条路径.因此O1是连通的.此外，由引理3，对于(λ，μ)∈O1，问题存在正的最小解(uλ，vμ).

对于任意的(λ1，μ1)，(λ2，μ2)∈O2，设k*=max{λ1，λ2，μ1，μ2}.由引理4可知，(k*，k*)∈O2，我们可以建立O2中的两条路径，分别从(k*，k*)到(λ1，μ1)和从(k*，k*)到(λ2，μ2).由此可知O2是连通的.证毕.

接下来，由定理1、引理3及引理5的证明，我们很容易获得临界曲线的上下界估计.这些估计只依赖于f、g、p、q以及Ω和BR上相应特征值问题的第一特征值，即：

定理2假设条件(H)成立，则

(0，λ*]×(0，λ*]⊂O1⊂(0，λ*]×(0，μ*]，

其中λ*由式(1)定义，λ*是问题(Pλ)的第一特征值，μ*是如下特征值问题

的第一特征值.

2 解的序和参数的序之间的关系

在这一节中，我们将给出解的序和参数的序之间的关系.

定理3假设条件(H)成立.设(λ，μ)∈O1，(u，v)是问题(Pλμ)的一对正解.则

(ⅰ)若λ≥μ且f≥g>0，x∈Ω，则ku≤v≤u，x∈Ω，其中

(ⅱ)若u≥v且g≥f，x∈Ω，则λ≥μ.

证明：(ⅰ)定义

将问题中的两个方程做差，所得等式两端同乘(u-v)-并在Ω-上积分，我们有

因此，Ω-=∅，即v≤u，x∈Ω.

由引理1可知，ku≤v，x∈Ω.

(2)

由引理1可知，u≤v，x∈Ω，即u=v，x∈Ω.

矛盾，即λ≥μ.证毕.