具有部分缺失数据混合几何分布总体的参数估计
王敏会
(青岛农业大学理学与信息科学学院,山东 青岛 266109)
0 引 言
几何分布是统计学中的一种重要的离散型概率分布,在生产实践中有着较为广泛的应用.文献[1-3]对几何分布的参数估计进行了研究.在进行统计分析时,经常会遇到缺失数据的情形,对缺失数据进行统计推断是一个重要的问题,文献[4-6]讨论了在缺失数据情况下多种常见分布的参数估计问题.混合分布用于描述不同分布按照一定的比例混合所构成的总体,混合分布模型在临床试验、可靠性分析等领域发挥着重要作用,对混合分布总体参数进行估计是很有意义的.文献[7-9]对混合指数分布、混合泊松分布、混合瑞利分布的总体参数进行了估计,李建丽等在文献[10]中运用EM算法对混合几何分布的参数进行了估计.对缺失数据的混合几何分布总体的参数估计目前还没有研究结果,本文运用矩估计法给出其满足强相合性及渐近正态性的估计量,并利用随机模拟说明此估计的可行性.
1 矩法估计及其渐近性质
假设存在一个混合几何分布总体,其概率函数为
其中:θ1、θ2为未知参数;q(0 首先考虑混合几何总体参数θ1、θ2的矩估计.对于观测(Xi,δi),i=1,2,…,n,建立矩估计方程: 其中 解方程组并整理,得 证明:因{δi,1≤i≤n}与{δiXi,1≤i≤n}均为独立同分布的随机变量序列,由强大数定律知 因此 令Σ=E(W1-EW1)(W1-EW1)T,则由多元中心极限定理可知 记 其中 a11=p(1-p) , (1) (2) (3) (4) (5) (6) 令 进而可知 (7) (8) (9) 证明:令 进而可知 (10) (11) (12) 下面通过随机模拟说明本文所给出的估计方法具有较好的估计效果. 我们对缺失概率p=0.05和p=0.1两种情形进行模拟.样本量n分别取为100、300和500,混合概率q分别取为0.2和0.4,变化参数θ1和θ2计算1 000次估计的均方误差.表1给出了混合概率q为0.2时的模拟结果,表2给出了混合概率q为0.4时的模拟结果. 表1 q=0.2时参数估计的均方误差 表2 q=0.4时参数估计的均方误差 从表1和表2中的模拟结果可以看出,对于不同的参数、不同的样本量、缺失概率以及混合概率,本文所给出的估计具有较小的均方误差,并且随着样本量的增加,估计的均方误差有减小的趋势.说明此估计方法具有可行性,且估计方法较稳健. 本文研究了在数据具有部分缺失情形下的混合几何分布总体参数的估计问题,证明了此估计量的完全相合性与渐近正态性.随机模拟结果能够说明此估计方法是可行的,因此具有一定的应用价值.

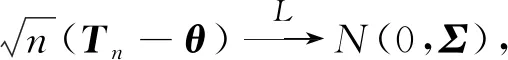






2 随机模拟


3 结 论

