古建筑三维点云数据的精简与配准方法

刘 冉 刘军廷

(宁波冶金勘察设计研究股份有限公司, 浙江 宁波 315000)

0 引言

中国古建筑代表了博大精深的文化,是人们伟大的创造、智慧的结晶。珍贵的古建筑文化遗产是社会经济、文化、政治发展的见证者以及优秀文化的传承者,同时也是研究我国古代文化和历史发展的重要资料。但是随着人类的影响，全球气候的变化,导致古建筑正在承受着不同程度的破坏[1]。因此，如何采用当今先进的科学技术使古建筑长存于世具有重要的研究意义。

三维扫描技术实现了高效、高精度、无接触的获取古建筑的三维点云数据[2],被广泛应用于三维重建来记录古建筑的三维数据、纹理特征,实现数字化的展示,已经成为获取数据的重要方式。但是由于古建筑的结构复杂,体积庞大,无法一次性获取整个古建筑的三维点云,因此需要对各站点云数据进行精简,然后再对其进行配准。

随着三维扫描技术的不断发展,获取的三维点云的质量也越来越高,可以更加详细逼真地反映出目标物体的结构以及细节特征,但同时也获取了很多冗余的点云。并且随着点云数据量的增加,也对处理的设备提出了更高的要求。因此需要对目标物进行精简处理,从而减少点云处理运行的时间,进而提高后续点云配准的效率,点云精简方法主要包括随机采样法[3]、曲率法[4]、包围盒法[5]、均匀格网法[6]等。

配准是古建筑三维重建的关键步骤。各站点云配准主要包括粗配准和精配准[7],粗配准主要是将两片点云转移到同一坐标系下,缩小位置上的偏差,为精配准提供良好的初始参数;精配准主要是在粗配准的基础上进一步优化粗配准结果,获取更高精度的配准参数。粗配准的方法主要包括以下方面：手动完成配准,通过手动在两片点云中选取至少3对以上的同名点,通过确定旋转、平移参数从而完成配准,该方法操作简单运行效率快,但其配准的结果容易受人为因素影响[8];超四点快速鲁棒匹配算法(super four 4 point robust matching algorithm,Super 4PCS)通过在源点云和目标点云中建立不共线四点集合,通过放射不变性原则完成初始配准,该方法可以获取较高的点云配准精度,但比较耗时,效率较低[9-10]。基于线特征和面特征的点云配准方法通过充分利用目标物点云中的线面特征,然后通过存在的约束条件实现配准参数的解算,获取的点云配准精度较高,但该方法仅适用于形状规则的建筑物点云[11-12]。

针对以上问题,本文提出对古建筑三维点云数据进行精简与配准方法的研究。首先对获取的点云进行数据精简,从而可以使点云均匀分布,并且保留一定数量的特征点,然后利用超四点快速鲁棒匹配算法和最近点迭代算法实现点云间的粗配准和精配准。该方法提高了点云配准的精度,并且提高了点云配准的效率。

1 点云数据的精简

点云精简的原理如下：目标物的原始点云M共包括m个点云,运用点云数据精简方法,将点云M精简为点云集合N,集合N共包括n个点云(n>0),从而在保留目标物结构特征的前提下,将点云数据量有效地缩减了。

1.1 包围盒随机抽样法

包围盒抽样法是在三维点云所在的坐标系中设置一个立方体包围盒,该包围盒可以包含整个三维点云模型,且其相互垂直的边与空间坐标系的三个坐标轴分别平行。将这个立方体包围盒分割成若干个边长为l的小立方体,每个小立方体中都包含若干个三维点云,统计在小立方体内的点云数量,最后对每个小立方体内的三维点云进行随机抽样,用抽取到的三维点云代表每个小立方体内原始的点云数据,并将其他的三维点云数据删除,从而完成点云数据的精简。该方法虽然获取的三维点云数据较为均匀,很好地避免了三维点云密度不一致的情况,但是该方法对包围盒内的所有三维点云进行同样的随机抽样方法,不能很好地区分具有明显特征的区域,会误删一定数量的特征点。

1.2 曲率精简法

曲率是对一个物体表面弯曲程度的衡量,物体表面某一点的曲率可以表示该点所在位置的方向变化,同时也反映出一个物体表面的特征点变化,物体表面的曲率值越大,则该处的几何特征变化就越明显,有特征点的数量就较多；相反,物体表面的曲率值越小,特征点数量越少,物体表面变化较小,区域较为平坦。因此,在曲率精简点云的方法过程中,在曲率较大的区域,点云数据精简的较少,保留的点云数量较多,而在曲率变化较小的地方,点云精简的力度越大,保留下来的点云数量较小。使用曲率精简点云数据,可以保留下更多的特征点,但是该算法在点云数据精简过程中不是均匀的,在点云数据较为平坦或者变化较缓慢的区域容易导致点云数据精简过多,从而导致点云数据产生空洞现象。

1.3 结合曲率-包围盒随机抽样法

古建筑的几何结构特征一般比较复杂,在对古建筑点云数据进行精简时,应该获取具有明显特征且均匀分布的点云数据,从而获取高精度的点云配准精度,因此结合两种方法的优缺点以及古建筑的数据结构特征提出结合点云曲率特征的包围盒精简方法,该方法既可以保留古建筑点云中的特征点,又可以实现平坦区域点云得到均匀分布,方法的具体步骤如下,流程图如图1所示。

图1 具体算法流程图

Stap1:首先遍历所有点云,求解每个点云的平均曲率并计算所有点云的平均值曲率和局部曲率,从而判断点云为特征点或者非特征点,即获取平坦的区域和特征点区域的分布。当点云的平云曲率值大于点云的局部曲率时,该区域为较为平缓的区域,反之为特征点明显的区域。

Step2：对获取的不同区域的特征点使用相应的方法进行点云数据精简,使用包围盒随机抽样法对平缓区域的点云进行精简,曲率法对特征点明显的区域进行点云精简,从而获取古建筑最终的点云精简数据。

2 古建筑点云数据的配准

2.1 精简点云的Super 4PCS粗配准算法

Mellado、Aiger等人在一致性四点集(4 point congruent sets,4PCS)的基础上提出的超四点快速鲁棒匹配算法(super four point robust matching algorithm,Super 4PCS),该方法可以用于任意姿态的点云数据配准,但是该方法是从原始的所有三维点云数据中选择的4点集进行源点云和目标点云数据的配准,由于原始点云数据量比较大,所以在使用该方法进行四点集选取的过程中,速度较慢,配准效率较低。因此,本文提出从精简后的原始点云和目标点云中选取四点集进行超四点集快速配准,有效地提高了四点集的搜索速度。该方法快速高效地实现了古建筑源点云和目标点云的初始配准,获取了初始配准参数,并且将目标点云转移到源点云所在的坐标系下,为精配准提供了良好的初始位置以及初始参数值。

2.2 基于ICP的点云精配准算法

本文提出的基于精简点云的Super 4PCS粗配准方法后,已经将古建筑源点云和目标点云实现了较高精度的拼接,但是由于噪声的影响,使得源点云与目标点云存在一点偏差,因此本文使用最近点迭代算法(iterative closest point,ICP)[13]进行粗配准后两站点云的精配准,该方法利用最小二乘方法通过在两片点云中搜索距离最小的同名特征点,通过多次迭代运算,缩小两个点之间距离,使得两点之间的距离小于设定的阈值时,停止迭代,从而解算出最优的配准参数,使粗配准后的源点云和目标点云重合,精配准的如式(1)所示。

(1)

式中,R是原始点云到目标点云的旋转矩阵;T是平移矩阵;pi是从粗配准后原始点云中提取的点;qi是从待配准点云中提取的与pi距离最近的同名特征点。

3 实验分析

为了验证本文方法的有效性,采用WHU-TLS基准数据集中的一座古建筑建筑物点云数据。选取的古建筑的源点云和目标点云如图2所示,点云信息如表1所示。

(a)源点云 (b)目标点云

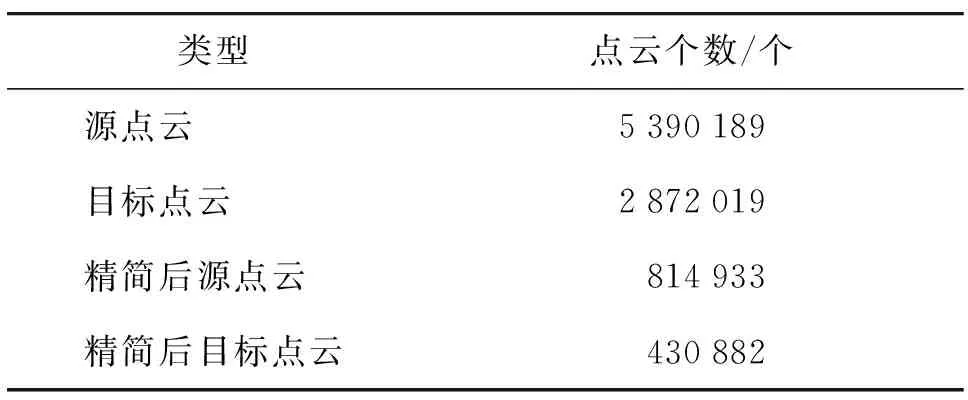
表1 古建筑源点云和目标点云数据的基本信息

图3为古建筑源点云和目标点云在配准前的初始位置分布,由图3可知,在配准前源点云和目标点云在空间位置上存在较大的偏差。

图3 古建筑的源点云和目标点云

古建筑具有结构复杂,数据量大的特点,利用本文提出的曲率-包围盒随机抽样法相结合的点云数据精简方法获取的精简后的源点云和目标点云如图4所示。获取的精简后的源点云和目标点云数据分别为814 933、430 882个,由图4可知,该方法减少了点云数据量,保留了古建筑几何特征,同时对非几何特征也均匀地保留了点云数量,有效地避免了出现点云空洞现象。

(a)源点云 (b)目标点云

对精简后的源点云和目标点云执行粗配准与精配准相结合的方法,获取最终的古建筑点云配准效果如图5所示。由图5可知,源点云和目标点云整体实现了较好的贴合,边界部门也融合较好,证明了本文方法的可行性。为了进一步证明本文配准方法的有效性,选取配准后源点云和目标点云的平均距离中误差作为衡量配准结果的精度指标,并与软件Geomagic Studio 12的配准结果进行对比。两种方法获取的古建筑点云配准结果的精度如表2所示。

图5 古建筑精配准效果图

表2 两种方法的配准结果

由表2可知,本文方法和软件Geomagic Studio 12分别获取的平均距离中误差为12.3、25 mm。由此可知,本文方法获取的点云配准精度优于软件Geomagic Studio 12。

本文也对使用包围盒随机抽样法、基于曲率法、曲率-包围盒随机抽样法相结合以及不对点云进行精简这4种方法对古建筑点云配准的效率以及精度影响进行了统计,各种方法获取的结果如表3所示。

表3 不同方法获取的配准结果

由表3可知,4种方法在整个古建筑点云配准过程消耗的时间分别为65、67、60、124 s,获取的配准后点云距离中误差分别为26、21、12.3、14.6 mm。由此可知,基于包围盒随机抽样法、基于曲率法的精简方法消耗的时间大致相同。但基于曲率的精简方法获取的点云配准精度优于包围盒随机抽样法,分析其主要原因可能是前者在精简点云过程中保留了古建筑中必要的结构特征点,而后者在点云精简过程中则被删除了,而保留了大部分较为平坦的地区;前三种方法的配准效率均优于没有进行点云精简的配准方法。主要原因分析是,在点云配准之前由于点云数量较多,在点云粗配准以及精配准过程中增加了搜索四点集和最邻近点的时间,综上分析,本文方法获取的点云配准结果无论是在配准时间还是在配准精度上都优于其他几种方法。

4 结束语

本文利用曲率与包围盒随机抽样相结合的方法对点云数据进行精简,从而减小点云的数据量,然后利用Super 4PCS算法进行源点云和目标点云的粗配准,最后利用ICP两片点云的精确配准。本文方法提高了整体源点云与目标点云的配准效率,同时也提高了配准的精度,为后续古建筑建模提供了一定的技术支持。