垄断企业产能投资、产品创新和过程创新的动态最优控制
戴晨阳
(上海交通大学 安泰经济与管理学院,上海 200030)
本文提出了一种垄断企业产能投资、产品创新和过程创新的动态最优控制模型。我们的研究源自Lambertini和Mantovani对产品创新和过程创新的研究,以及JØRgensen对于企业产能投资的研究,将三种投资决策结合研究,以便更加贴合企业的实际决策情况。
此前,学者已经将企业的创新模式区分为产品创新和过程创新并进行了详细的研究。Pan和Li认为产品创新意味着企业通过对现有产品进行研发、更新,提升自有产品的质量、扩展产品功能,能够提高消费者对于公司产品的保留价格,也意味着公司面临的需求曲线外移;认为过程创新一般为公司对自身产品工艺流程进行技术改造,以此来降低产品的边际生产成本。
通常情况下企业倾向于同时执行产品创新和过程创新。为了便于企业制定更为合理、准确的创新策略,学者一直致力于探索企业在发展历程中如何对两种创新方式进行抉择。Mantovani认为产品创新和过程创新共同运行时会产生互补效应,企业并不应该分散其创新业务并试图找出哪一项更为有利。但当把视角转向产品的技术生命周期研究时,Maski 发现产品创新和过程创新之间存在替代效应。
在产品生命周期的研究中,普遍的观点是产品创新必然先于过程创新,有许多个研究结论能够支撑这一理论。Lambertini和Rossini认为企业首先需要通过研发努力设定相互的差异化程度,然后在市场上进行质量竞争或价格竞争。Abernathy和Utterback、Abernathy和Utterback同样认为公司最初更加倾向于将大部分研发资源用于产品创新,因为市场初期潜力巨大,往往需要找到合适的产品来迅速拓宽市场;后期随着大量产品涌入市场,整体盈利能力会出现快速下滑,公司会将资源转入过程创新力求控制产品的生产成本。Klepper认为企业会在初始阶段更多地专注于产品端的研发,因为初始阶段产品的创新能够使得企业快速获得更多新的消费者扩大下游的需求,以此来增加企业的收入,然后企业会在产品发展的后期返回过程创新的阶段。而Adner和Levinthal则认为传统的生命周期研究方法有失偏颇,认为传统的研究方法过多地专注在企业内部的能力上,他们提出了一种基于技术创新和消费者异质化需求之间相互影响的研究方法。不同的是,他们认为生命周期的第一阶段并不会总伴随着大规模的产品创新,这将取决于产品最初在市场上的表现。第二阶段同样也将是过程创新占据主导地位,但这并不意味着此时产品创新会发生断崖式下滑。相反,他还认为生命周期中可能还存在有第三阶段,此时产品创新和过程创新是相互平衡的,以此来实现价格的相对稳定,并同时提升产品的性能。Adner和Levinthal和传统观点之间的差异主要来自,他们认为对于企业而言他们的新产品对市场而言并不一定是完全的创新。就比如iPhone之于世界和小米之于世界,两者的起点是完全不同的,所以不同的企业在初始阶段也会有不同的研发策略。
与以上不同的是,Lambertini和Orsini、Zhong和Zhang在需求不变、产品质量提升会提高产品价格的假定下发现,产品创新和过程创新是两种完全独立的决策且只与固定的需求相关。
1 基本模型
本文在连续有限时间t∈[0,T)上建立一个垄断厂商的最优控制问题,在任意一个时间点,垄断厂商可以选择用于产能、产品创新和过程创新的投资水平。首先依据JØRgensen的假设认为垄断厂商始终保持满负荷生产且没有库存,即垄断厂商t时刻的产量与其产能和需求相等,且产能会随着企业的投资而增加。以下为企业产能投资的动态微分方程:
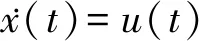
(1)
其中,x(t)为企业在t时刻拥有的产能,u(t)为企业在t时刻对于产能的投入。企业在t时刻产能投资的总成本为e·u2(t),e为大于0的恒定参数,衡量了企业产能投资的效率。
假设企业在时点t的产品质量会随着企业在产品创新的投入而增加,时点t的边际成本会随着企业在过程创新的投入而降低,根据Lambertini和Mantovani的研究可以得到以下动态微分方程:

(2)

(3)
其中,q(t)为企业在t时刻的产品质量,k(t)为t时刻对产品创新的投资,c(t)为企业在t时刻的边际生产成本,α(t)为t时刻对过程创新的投资。假设质量q(t)会随着时间而衰减,边际生产成本c(t)也会随着时间而增长,分别用γ∈[0,1]和η∈[0,1]表示产品质量和边际成本所具有的恒定不变的衰减率。企业在t时刻投资于产品创新和过程创新的总成本分别为h·k2(t)和f·α2(t),h和f分别是产品创新和过程创新的投资效率,皆为大于0 的恒定参数。所以厂商在t时刻生产x(t)个产品的总成本为
C(t)=c(t)·x(t)+e·u2(t)+h·k2(t)+f·α2(t)
(4)
假设公司产品创新的效率低于过程创新,且产品质量的衰减率高于边际成本,即h>f,γ>η。如iPhone、数码相机等新产品问世后,质量提升往往意味着技术的更迭,而过程创新则可以通过优化生产模式等多种方法实现,所以假设产品创新的效率低于过程创新是合理的。此外,消费者对于产品质量的更迭有着更高的要求,而生产成本的衰减则多来自设备的老化,是一个相对较慢的过程,所以假设产品质量的衰减率高于边际成本也是合理的。
根据Pan和Li的模型,假设消费者在t时刻的需求x(t)由产品价格p(t)和产品质量q(t)共同决定,反需求函数为如下形式:
p(t)=a+b·q(t)-x(t)
(5)
所以厂商的瞬时利润为
π(t)=[a+b·q(t)-x(t)-c(t) ]·x(t)-e·u2(t)-h·k2(t)-f·α2(t)
(6)
假设企业追求t∈[0,T)时间内的现值最大化,则垄断企业基于产能、产品创新和过程创新的模型为
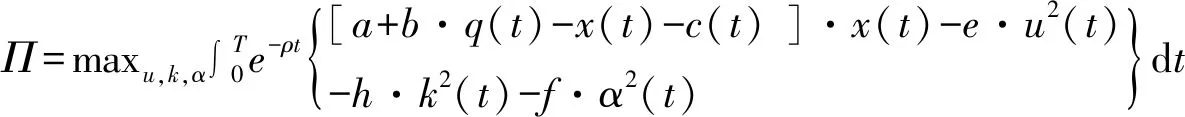
(7)
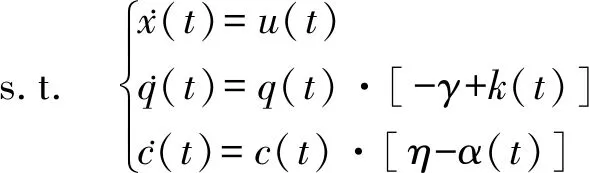
(8)
在此模型中,ρ为恒定不变的贴现率,垄断厂商的控制变量分别是公司产能的投资u(t)、产品创新的投资k(t)和过程创新的投资α(t),状态变量分别是企业产能x(t)、产品的质量q(t)和产品的边际成本c(t)。
2 模型求解
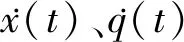
H=[a+b·q(t)-x(t)-c(t) ]·x(t)-e·u2(t)-h·k2(t)-f·α2(t)+λ1(t)·u(t)+λ2(t)·q(t)·[-γ+k(t) ]+λ3(t)·c(t)·[η-α(t)]
(8)
企业实现贴现利润最大时,函数(8)的一阶条件为
(9)
(10)
(11)
共态方程可以表示为
(12)
(13)
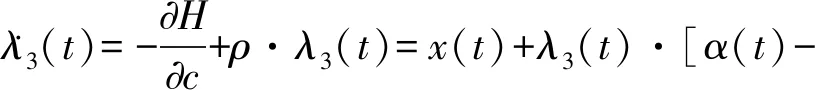
(14)
方程(12)、(13)和(14)的横截性条件分别为
λ1(T)≥0,x(T)≥xmin,(x(T)-xmin)·λ1(T)=0
(15)
λ2(T)≥0,q(T)≥qmin,(q(T)-qmin)·λ2(T)=0
(16)
λ3(T)≥0,c(T)≥cmin,(c(T)-cmin)·λ3(T)=0
(17)
将方程(9)、(10)和(11)分别对时间t求导得
(18)
(19)
(20)
将方程(18)、(19)和(20)分别代入方程(12)、(13)和(14)后得
(21)
(22)
(23)
同时我们还有
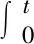
(24)
(25)
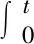
(26)
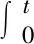
(27)
所以通过方程(21)可以得到
(28)
(29)
结论1由方程(28)和方程(29)可以看出,垄断厂商对于产能的投资增长率与产品创新和过程创新的投入成反比。
根据方程(1)和方程(21)有
(30)
(31)
结论2由方程(30)和方程(31)可以看出,产品创新的投资增长率与过程创新的投资量呈正相关关系。同样,过程创新的投资增长率与产品创新的投资量也呈现正相关关系。
(32)
(33)
(34)
将方程(33)和(34)代入方程(32)得到
(35)
由方程(35)可得
(36)
(37)
(38)
(39)
(40)
(41)
结论3垄断厂商产品创新投资与过程创新投资之间呈正相关关系。
产品创新与过程创新的互补关系与Mantovani、Athey和Schmutzler的研究相符。因为产品创新能够外移需求曲线,当需求更大时,降低单位成本的回报最高,因此公司将倾向于同时投资产品和过程创新。
结论4垄断厂商产能投资与产品创新投资成正比、与过程创新投资成反比。
产品创新能够外移需求曲线,而在本文的假设下企业需要先进行产能投资扩充产能后才能满足增加的需求,故而产能投资和产品创新投资成正比关系,垄断厂商倾向于同步进行这两种投资。另一方面,过程创新会随着产能的增长而获得更大的边际收益,因此依据产品周期理论企业会在产业早期倾向于将大部分资源用于产能投资和产品创新,在产业后期产品创新边际收益较小的情况下大力投资产品创新,这也与Abernathy和Utterback的产品周期理论相吻合。
结论5垄断厂商在能够实行产能投资、产品创新和过程创新的情况下,um、xm、km、qm、αm、cm是唯一的鞍点均衡。
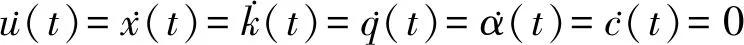
um(t)=0
(42)
(43)
km(t)=γ
(44)
(45)
αm(t)=η
(46)
(47)
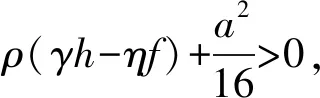
3 稳定性分析
该动态模型的稳定性可以通过分析微分方程(1)、(2)、(3)、(21)、(22)、(23)相对应的6×6的雅可比矩阵得出,对应的雅可比矩阵为
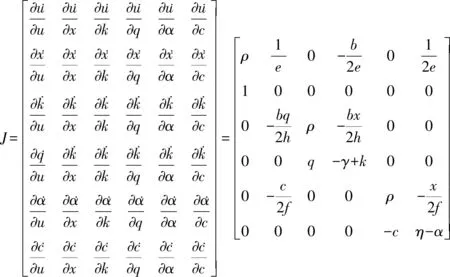
(48)
显然矩阵(48)的行列式并不能根据已有信息去判断其符号,同时该举证对应的特征值的表达式亦过于复杂,故此处采用数值计算的方法。为了通过数值计算的方法证明模型的稳定性,本文通过参考Lambertini和Mantovani、Pan和Li的文章得到合适的参数如表1、表2 所示。

表1 数值计算中参数的值
代入方程首先可以得到xm=5.00,km=0.01,qm=1.8·10-4,αm=0.02,cm=2.48·10-4。进而用{ξ1,ξ2,ξ3,ξ4,ξ5,ξ6}表示矩阵(43)的6个特征值,通过表1以及控制变量和状态变量的稳定解,可以解得
{ξ1,ξ2,ξ3,ξ4,ξ5,ξ6}≃{0.63,-0.53,0.09,0.10,0.01,-0.002}

表2 数值计算中参数的值
同样,代入方程首先可以得到xm=4.99,km=0.01,qm=5.13×10-4,αm=0.2,cm=2.49·10-2。进而用{ξ1,ξ2,ξ3,ξ4,ξ5,ξ6}表示矩阵(48)的6个特征值,通过表1以及控制变量和状态变量的稳定解,可以解得
{ξ1,ξ2,ξ3,ξ4,ξ5,ξ6}≃{0.63,-0.53,0.20,-0.10,0.09,0.01}
通过重复同样的运算可以发现有两个特征值为负,所以{um,xm,km,qm,αm,cm}是稳定的。
4 结论
本文运用动态最优控制理论的模型找到了垄断厂商关于产能、产品创新和过程创新的最优投资水平。相较于JØRgensen在寡头垄断下讨论厂商对于产能的投资,本文从一个新的视角探讨了垄断厂商在整个产品的发展过程中对于产能、产品创新和过程创新的抉择;同时和需求不确定模型、简单的内生增长模型不同,本文认为需求的增长来自企业对于产品创新的投资,同时考虑了过程创新降低边际生产成本的情况。与Lambertini和Orsini的模型相比,本文认为厂商首先需具备生产能力才能够完成相应产品的生产,也更贴合产品市场早期产能较小的特征,使得对产品生命周期的研究更为完善,同时消费者的需求会随着产品质量的提升而增长。本文通过分析得出,垄断厂商对于产能投资的增长率与产品创新和过程创新成反比,表明当企业开始进行创新时,企业对于产能的投资增速将会减缓;垄断厂商产能投资与产品创新投资成正比、与过程创新投资成反比,表现为企业在产业早期的投资主要集中于产能和产品创新的投资,这也与Lambertini和Rossini的论证一致。此外,本文还发现,产品创新与过程创新之间呈互补关系,契合Mantovani的结论,与Lambertini和Orsini得出的两种创新之间独立不同。当然,文章依然有一定的不足之处,与JØRgensen的研究相比,本文并未考虑寡头垄断下产能投资的决策问题;与Zhong 和Zhang的研究相比,文中并没有考虑知识积累对于整个创新过程的影响;与Mantovani的研究相比,文中并没有考虑产品创新和过程创新之间本身所具有的互补关系。

