基于准比例谐振控制器的5相感应电机电子变极研究
贾慧利
(1.芜湖职业技术学院汽车与航空学院,安徽 芜湖 241006;2.浙江大学电气工程学院,浙江 杭州 310027)
0 引言
感应电机自身结构简单、成本低,具有宽广的速度范围以及优越的弱磁调速性能。多相电机由于相数的增加,其突出的优势有转矩输出更加平稳,振动和噪声低,可运行在不同控制平面满足不同工况的需求,使电机运行性能提高[1-2];其驱动系统可靠性高、容错效果好[3-5]。多相感应电机兼具2者的优点,非常适合重要的工业领域如智能化汽车驱动系统、航空驱动系统等[6],这些应用领域的电机需要同时满足低转速时输出大转矩和宽广的调速范围[7],其中电子变极技术是实现这些要求的便捷方法之一,即改变极对数来扩大电机的转速和转矩范围,在低速时采用大极对数,在高速时采用小极对数,实现低速大转矩和宽广的恒功率运行范围[8]。但是电机在电子变极过程中存在转矩和转速的波动大,系统运行不平稳和动态响应滞后等问题,影响了电子变极技术的应用,因此提高电子变极过程中电机运行性能和控制精度是多相感应电机电子变极领域的研究热点。
近年国内外多位学者在多相感应电机变极领域进行研究:Osama等[9-10]在一台6相电机上实现了1对极和2对极之间的基本电子变极,拓宽了恒功率运行范围;对阶跃响应和斜坡响应电子变极的仿真对比分析,验证了斜坡响应性能优于阶跃响应。钱罗奋[11]提出一种交流电机 2Δ /3Δ 换相变极法,在不断电条件下实现电机换相变极,采用的是一种传统的接触开关控制的变极方法,变极切换过程存在不连续问题。Ge[12]等在一台9相电机上通过基于斜坡响应的PI电流控制技术实现了电子变极,但动态响应性能较慢。Ershad等[13]对9相电机在空载条件下电子变极进行实验和分析。Umesh等[14]对9相感应电机变极运行在4极和12极的模式下减小转矩脉动等进行研究。Libbos等[15]对多相感应电机变极的选极策略从转矩和速度两方面进行研究。Latif[16]对多相感应电机的4极到8极电子换极研究,以提升电子变极过程中转矩平稳。笔者所在课题组对5相感应电机(five-phase induction motor,FIM)的电子变极技术的响应方法和变极电流控制策略方面分别做了深入研究[17-18],使变极过程中的电磁转矩波动和超调量减小。
基于上述研究,为了进一步提高FIM电子变极过程中转矩、转速动态响应性和减小其波动,同时改善变极前和变极后电机在稳态时的运行性能,设计适于电子变极的准比例谐振(quasi proportional resonance,QPR)电流控制器:首先改进传统比例谐振得出QPR,根据电子变极前后谐波不同加入相应的谐波抑制算法,再对QPR变参数化设计使谐振频率点随电机转速自适应变化;其次,采用预修正Tustin变换离散化保证QPR控制器的稳定性;最后,设计QPR控制,随电机运行平面的改变来切换相应的谐振频率,对电子变极前后实施2段式精准控制,并在Speedgoat多相电机半实物仿真平台上对所提控制方法进行实验验证。
1 FIM数学模型和电子变极
1.1 电压和转矩方程
多相感应电机在自然坐标系下的电压方程如式(1)所示:
(1)
式中:U为电压;I为电流;R为电阻;Lsr为互感矩阵;下标号s为定子参数;下标号r为转子参数。
转矩方程如式(2)所示:
(2)
式中:Te为电磁转矩;θ为转子的电角度。
采用的恒幅值变换矩阵Cs如式(3)所示,可将多相感应电机的定子电流、电压等效变换成同步速坐标系下的直流分量。
Cs=
(3)
式中:x为谐波次数;θ1,θ2,θ3,…,θx为x次谐波在任意速坐标系下的相位电角度;n为电机相数。当α=2π/n时,电机有偶次谐波平面。矩阵的第1和2行构成q1-d1平面,为基波平面;第3和4行构成的q2-d2面即2次谐波平面,以此推断可得x次谐波平面。
由集中整距绕组分布的多相电机的坐标变换矩阵式(3)可得,其变换后则形成m个相互正交的控制平面,即有m个自由度,在旋转坐标系下各谐波平面相互解耦。当n为奇数时,m取值为(n-1)/2。
多相感应电机在基波q1-d1平面和x次谐波qx-dx平面的电压和转矩方程表达式如式(4)所示:
(4)
式中:下标号xds为x次谐波平面的定子d轴分量;xqs为x次谐波平面的定子q轴分量;xdr为x次谐波平面的转子d轴分量;xqr为x次谐波平面的转子q轴分量;p代表微分运算;Lxm为x次谐波平面的互感,Lx0s为x次谐波平面的定子漏感;Lx0r为x次谐波平面的转子漏感;Rxr为x次谐波对应的折算后转子电阻;ω为定子电角度;ωr为转子电角度;Txe为x次谐波的电磁转矩;np为极对数。
1.2 FIM的电子变极基本原理
本文实验所用的FIM,其绕组结构图如1所示,有偶数次谐波,即可以实现基波平面和2次谐波平面之间的电子变极切换。

图1 试验用FIM绕组结构
FIM的d1-q1和d2-q2平面如图2所示。

图2 实验用FIM d1-q1和 d2-q2平面
d2-q2平面在d1-q1平面上的投影是0轴上的一个点,反之亦然。d1-q1和d2-q2为FIM正交的2个控制平面,这决定其有2个控制自由度。基波相电流在d1-q1平面则形成1对极旋转磁场,2次谐波相电流在d2-q2平面则形成2对极旋转磁场。电子变极的基本原理是:在转子磁场定向矢量控制的基础上,把定子电流分解为激磁电流分量i1ds、i2ds和转矩电流分量i1qs、i2qs,变极的切换本质就是i1ds、i2ds和i1qs、i2qs相互切换的过程,在此过程中进行电流的分配,顺利完成变极。
2 QPR控制的电子变极
2.1 基于PI电流控制器的电子变极
基于转子磁场定向矢量控制,电机电子变极过程中的激磁电流分量为i1ds、i2ds,转矩电流分量为i1qs、i2qs,根据电磁转矩直接跟踪方法,对i1qs、i2qs由T1e、T2e取代,切换的过程选取斜坡响应的方法来实现电子变极调速,以1对极向2对极变换展示,如式(5)所示。
(5)
式中:t为变极的动态时间减去变极的开始时间;Tm为变极全过程的总时间。上标*代表分量为给定的参考值,k1、k2为常系数。
FIM的传统PI电流控制器,其经过坐标变换在离散域中数学表达如式(6)所示:
(6)
式中:k1p为基波平面的电流环比例系数;k2p为2次谐波平面电流环比例系数;k1i为基波平面的电流积分系数;k2i为2次谐波平面电流积分系数。
设G(z)为FIM的数学模型,结合式(6)可得FIM基于传统PI电流控制器的结构框图如图3所示:

图3 FIM的传统PI电流控制器结构
设定反馈的定子电流idq1s=[id1s,iq1s],idq2s=[id2s,iq2s],则由图3可得其表达式为:
(7)
得出跟踪输出表达式:
Y(t)=kt-c+be-mt
(8)
式中:c为大于零的常数,其取值受电机参数和PI参数两方面影响;b、m为实数。
FIM基于传统PI电流控制器的电子变极控制如图4所示。

图4 基于传统PI电流控制器的FIM电子变极控制
2.2 所提QPR电流控制的电子变极
传统的比例谐振控制器可无静差跟踪控制和减小干扰[19],相较于PI控制,其减少了Park坐标变换,简化了运算且适用于多相感应电机的容错控制。
2.2.1 传统的PR控制器
传统的 PR 控制器其传递函数为:
(9)
式中:Kp为比例增益;Kr为积分增益;ω0为谐振频率即电机中的电角频率。
PR在非谐振频率点处增益低且频带宽,不能抑制非谐振频率点处的干扰信号。
2.2.2 加入阻尼项修正的QPR控制器
在传统的PR控制器中加入阻尼项进行修正,即为QPR控制器。通过加入阻尼项修正,可为控制器设定满足要求的谐振点增益,适当增加带宽,适度降低系统的灵敏度,以适于多相感应电机的控制,GQPR(s)传递函数为[20]:
(10)
式中:ωc为截止频率;Kr的作用是控制稳态误差,且其取值会影响基波频率处的增益。
ωc与系统的带宽成正比,决定信号的选择性且和信号的选择性成正比关系,选取适当的ωc值,可以保证电机在一定的速度范围内实现大增益。
2.2.3 加入谐波抑制项的变参数QPR控制器
由于多相感应电机谐波含量较多,可进一步利用QPR控制器的谐波抑制特性,在QPR控制器上叠加需要抑制的第n次谐波抑制项。谐波抑制项GHC(s)的传递函数为[21-22]:
(11)
绕组结构为π/n相带分布时,谐波次数为:3、5、7、11、13次等;而本实验FIM绕组结构为 2π/5 相带分布,则含有偶次谐波;根据电机变极前后运行平面不同,选择抑制不同的谐波。
QPR控制器需要根据电机转速的变化自适应地调整控制器的谐振频率点,即转化为变参数QPR。
将ω0=2πf代入式(11),则变参数QPR的GVHC(s):
(12)
对于绕组结构为 2π/n相带的多相感应电机,其加入谐波抑制的变参数QPR的传递函数GVQPRHC表达式如(13)所示:
(13)
2.2.4 变参数QPR预修正Tustin变换离散化
变参数QPR要用数字控制器进行控制须离散化处理。而基于广义积分器的数字离散化会使控制系统的稳定性能变差[23],采用Tustin 变换离散化处理能有效保证系统的稳定性,其表达式为[24]:
(14)
式中:Ts为采样时间。
但这种Tustin 变换离散化后会导致积分器谐振频率出现偏差,为抑制该缺点,将其优化为预修正Tustin 变换如式(15)所示:
(15)
由ω0=2πf,得:
(16)

根据实验用FIM特性取值ωc为πf/25,用ωc的取值和式(16)代入式(13),得到离散化的有谐波抑制项的变参数QPR传递函数:
(17)
2.2.5 QPR电流控制器设计
基于静止坐标系,根据式(17)为FIM设计1控制平面和2控制平面的QPR电流控制器。以1平面的电角速度ω1和转差频率ω1s算得f1构建1平面QPR控制器。同理以由ω2和ω2s算得f2构建2平面QPR控制器,其结构框图如图5所示。

图5 设计的QPR控制器结构
FIM基于转矩电流切换和QPR控制器的电子变极控制过程:1平面工作时使用1平面QPR控制器符合电机的频率f1,2平面工作时使用2平面QPR控制器符合电机的频率f2,2个QPR控制器工作的切换时刻为电子变极过程的中间时刻。基于QPR电流控制器的电子变极控制如框图6所示。
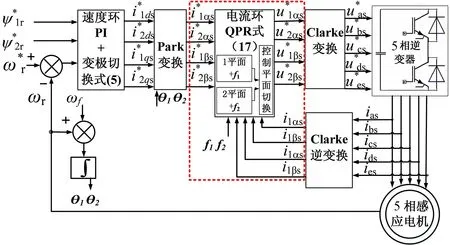
图6 基于QPR电流控制器的FIM电子变极
3 试验结果及分析
搭建基于Speedgoat的FIM试验平台如图7所示,对所提QPR电流控制器进行电子变极试验验证。试验FIM的参数如表1所示。

图7 基于Speedgoat的 FIM试验平台
FIM的试验条件设定为转速1 600 r/min,1控制平面QPR的参数选取值为:f1取28.9 Hz,k1p取9,k1r取30;2控制平面QPR的参数选取值为:f2取59.2 Hz,k2p取10,k2r取20。f取值方法为:试验电机在1控制平面工作时极对数为1,基于此根据转速算得频率,然后加上滑差频率得到f1;试验电机在2控制平面工作时极对数为2,基于此根据转速算得频率,然后加上滑差频率得到f2。

表1 FIM的基波和谐波平面参数
对FIM加载15 N·m,选取1对极向2对极变极,变极过程为1 s,在图中以虚线方框圈出,虚线圆框为变极结束后的波形。
图8为基于PI电流控制器的FIM电子变极的实验波形。由图8a基波平面和谐波平面的转矩电流iq1s、iq2s的波形可见,在电子变极结束时iq2s未达到参考值,iq1s未达到零值,要在变极结束后延迟约0.5 s,iq2s才稳定在参考值,iq1s才接近0;说明基于PI电流控制的转矩电流动态响应滞后,不能按照给定的斜坡曲线和时间完成变极。转矩电流动态响应滞后,进而导致相电流图8b变极结束后0.5 s时仍有较大波动,且最大波动峰值约14 A,波动持续时间长,使电机运行不平稳的时间延长;由转速图8c可得变极结束后0.5 s时才接近稳定值1 600 r/min,在电子变极过程中转速波动值约有160 r/min左右。从图8d中可见电磁转矩的波动时间长,在变极结束后0.5 s还未完全稳定在15 N·m,且波动峰值达到约19.5 N·m,转矩波动大且持续时间较长。
图9为基于所设计的QPR电流控制器的FIM试验波形。由图9a可见变极过程中转矩电流iq1s和iq2s的变化情况,iq1s和iq2s整体变化过程比PI控制时更加平滑,在变极的起始段和结束段iq1s和iq2s的超调更小,在变极结束时刻iq1s和iq2s几乎无延迟地稳定在参考值,相较于PI控制的转矩电流达到稳态要延迟0.5 s,其动态响应快33%;且在变极全过程中过渡平滑超调小,有效削弱电机的抖动问题。由图9b可得,相电流在变极结束时刻,即达到稳定值,波动峰值11.5 A,明显低于PI电流控制的波动峰值14 A,相较于PI控制变极相电流峰值波动小约25%;由图9c转速及其局部放大图可得,变极结束时刻转速即可稳定在1 600 r/min,在电子变极过程中转速波动约为80 r/min左右,相较于PI控制变极转速波动小50%。从图9d中可得电磁转矩在变极结束时刻即可达到稳定值15 N·m,且波动峰值约16.5 N·m,小于PI电流控制的19.5 N·m,相较于PI控制变极转矩波动小20%。由图9的数据可见,采用设计的QPR电流控制器,使FIM系统在电子变极过程中动态响应性明显提高,转矩和转速波动明显减小,转矩电流过渡平滑且超调小,有效削弱了电机抖动。

a.iq1s、iq2s(1对极→2对极)

b.相电流(1对极→2对极)

c.转速(1对极→2对极)
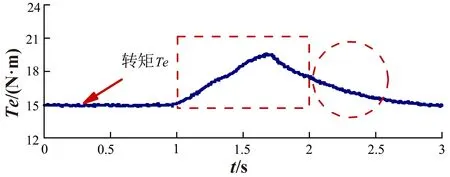
d.电磁转矩(1对极→2对极)图8 基于PI电流控制器的电子变极波形
通过对比图8b和图9b中稳态时相电流放大图可得,采用所提QPR电流控制器,在1对极稳态工作时相电流正弦性更好,说明谐波抑制算法同时改善了电机的稳态运行性能,同理在2对极稳态工作时同样有效,提高了FIM在不同运行平面的稳态性能。

a.iq1s、iq2s(1对极→2对极)

b.相电流(1对极→2对极)
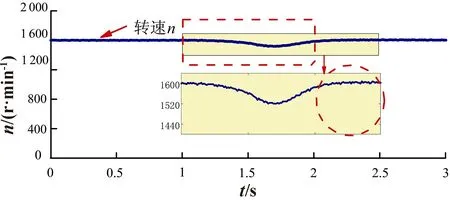
c.转速(1对极→2对极)

d.电磁转矩(1对极→2对极)图9 基于QPR电流控制器电子变极试验波形
4 结论
1)在FIM电子变极过程中采用所设计的QPR电流控制器取代PI电流控制器,可明显提高转矩电流的动态响应性,有效降低转矩和转速波动,使变极过渡更加平滑。
2)采用2段式QPR电流控制器可随着变极前后电机频率的不同对FIM实施更加精准的控制,以及加入对应的谐波抑制算法,均可有效减小FIM在电子变极动态切换程中的抖动,另外谐波抑制算法改善了电机稳态时相电流的正弦性。
3)QPR电流控制器基于静止坐标系,其算法更加简单,且适于电机的容错控制。接下来将开展基于QPR控制的多相感应电机电子变极容错技术研究。

