基于WPT和参数优化的VMD谐波检测方法
施瑶,王雅静,梅宇,刘士绮
(山东理工大学 电气与电子工程学院,山东 淄博 255049)
0 引 言
随着新能源分布式电源的并网运行,以及各种电力电子元件在电力系统中被大量地使用,由此引发的电力系统安全稳定问题受到了广泛地关注[1-2]。这些非线性负载与设备运行使得电力系统受到的谐波污染加重,准确地测量出谐波分量并对这些谐波分量进行处理对电力系统安全可靠地运行具有重要意义[3-4]。
目前,谐波检测常用方法包括傅里叶变换 (Fast Fourier Transform, FFT) 算法[5]、小波变换算法[6]、经验模态分解(Empirical Mode Decomposition, EMD) 算法[7]等。FFT计算速度快,但其频率分辨较低,对相近的频率成分无法检测,且算法存在频谱泄漏和栅栏效应等问题[8]。小波变换算法能够克服FFT的缺点,具有较好的时频特性,但其分析结果易受所选择的小波基函数影响,且相近频率无法有效分离,限制了其应用[9]。EMD算法具有不需要选择基,实现简单的优点,但信号若存在噪声时,不易分解出单一分量,且存在模态混叠问题,无法保障检测精度[10]。
变分模态分解(Variational Mode Decomposition, VMD)算法是一种新的信号处理方法[11]。VMD算法将信号分解为K个解析分量,K值需要提前设定,若K值选择合适则能克服模态混叠问题。文献[12]首次将VMD用于谐波检测,但并未说明如何选取合适的K值。文中以VMD分解在谐波检测中的瞬时频率为基础,提出一种新的K值选择方法,并考虑到在实际的采集中往往伴有噪声干扰[13],影响VMD分解的谐波质量,文章先利用小波包降噪(WPT)方法对谐波信号进行降噪处理[14],对降噪后信号进行VMD预分解,通过瞬时频率变化选择合适的K值,最后对信号进行最优K值VMD分解并利用希尔伯特变换提取参数。仿真结果与对比验证了文章算法的有效性与准确性。
1 变分模态分解
VMD将谐波信号分解为K个有限带宽的模态分量,通过迭代搜索变分模型最优解确定每个本征模态分量(Intrinsic Mode Function,IMF)的中心频率和带宽[15]。
uk(t)=Ak(t)cos(φt(t))
(1)
式中Ak(t)为IMF分量uk(t)的瞬时幅值;φt(t)为瞬时相位函数,且φt(t)≥0;IMF的瞬时频率为ωk(t)=dφk(t)/d(t),同样ωk(t)≥0。
1.1 变分模型
谐波信号经过VMD算法处理后得到K个IMF分量,通过如下方式估算每个IMF的中心频率和带宽:
(1)利用对模态分量uk的Hilbert变换计算得到uk(t)的解析信号;
(2)加入指数项ejωkt估计每个解析信号的中心频率,并将uk(t)的频谱调制到基频带上;
(3)计算解调信号梯度的平方L2范数,估计带宽。
通过上述步骤得到的变分约束模型为:
(2)
式中δ(t)为单位脉冲信号;j为虚数单位;*表示卷积;∂t表示对函数求时间t的偏导数。
1.2 变分模型求解
将约束变分问题转化为非约束变分问题,引入拉格朗日惩罚算子λ(t)和二次惩罚因子α,增广拉格朗日表达式如式(3)所示:
L({uk},{ωk},λ)=
(3)
VMD利用交替乘法算子方法求解变分模型式(3)的最优解,具体流程如下:

(2)令n=n+1,开始执行整个迭代;
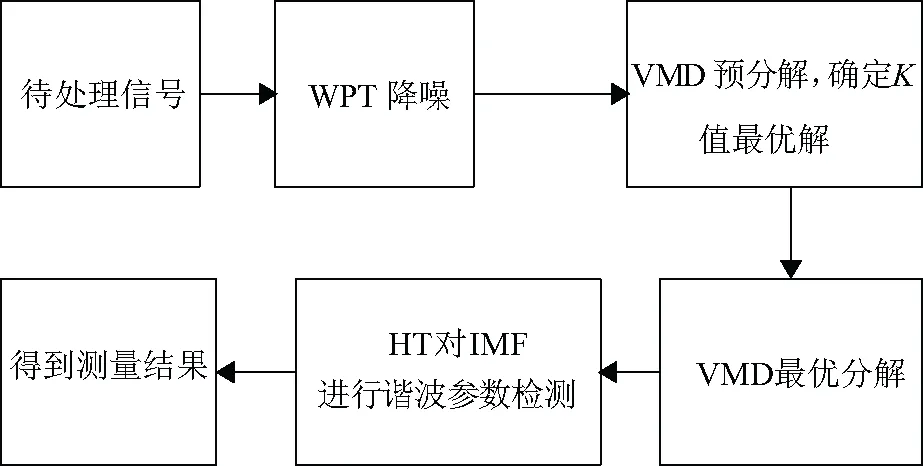
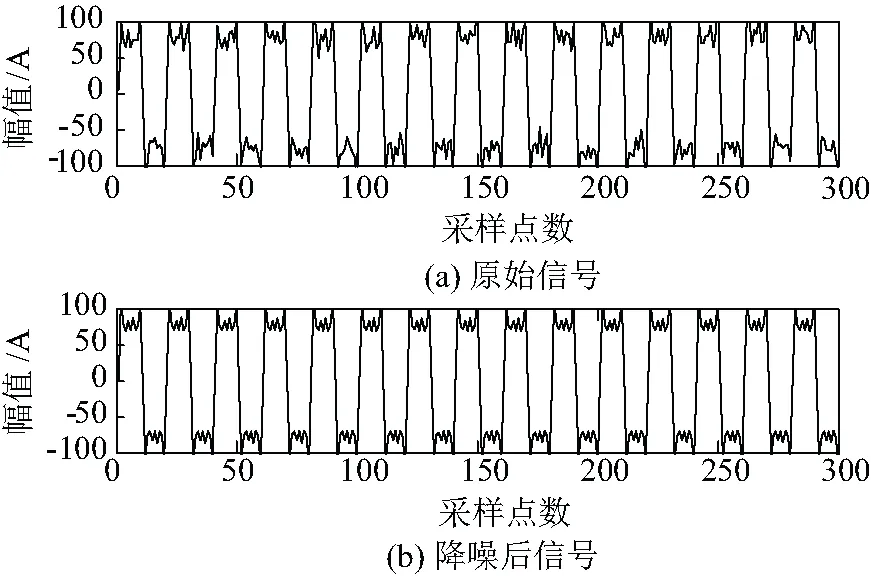
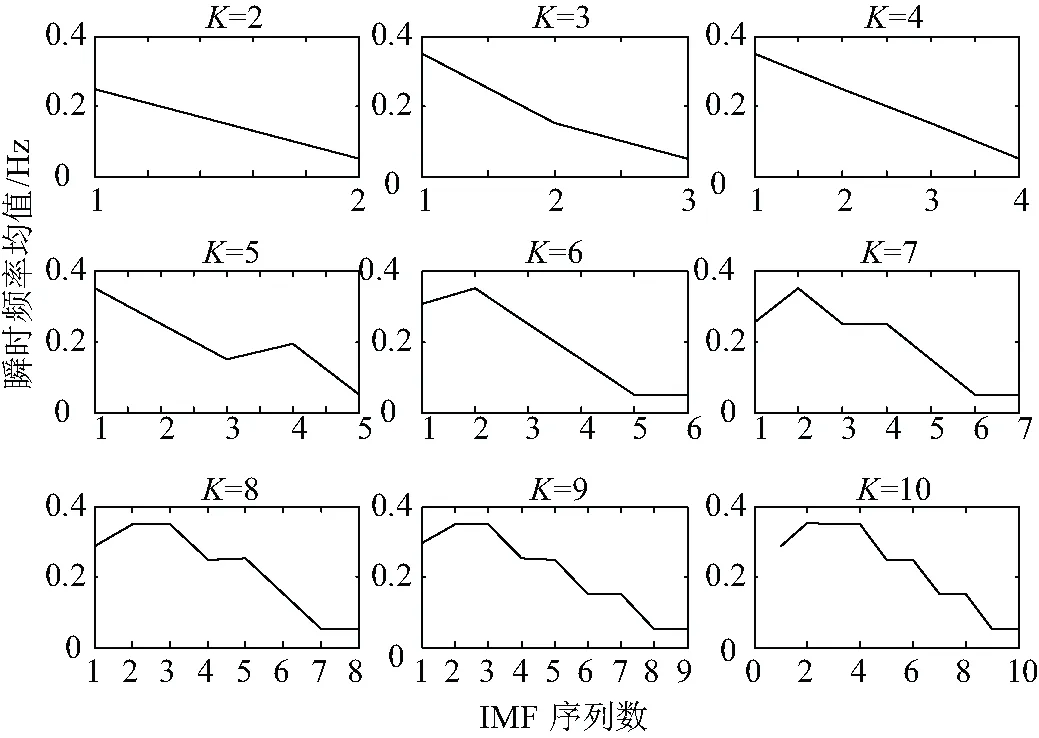
(3)令k=1,k (4) (4)k (5) (5)更新λ: (6) (6)循环步骤(2)~步骤(5),直至满足式(7)迭代停止条件,结束循环: (7) 式中ε为判别精度,且ε>0。 通过上述步骤,VMD算法将谐波信号分解为K个IMF分量。 VMD算法易受噪声影响,分解得到的调幅-调频模态分量uk波形产生畸变,无法保障后续测量的准确性[16]。因此,需要对含噪谐波信号进行降噪预处理,降低噪声对VMD算法影响。 小波包降噪理论基础完善,降低噪声的同时能够较好地保留信号有效信息,保障后续测量的准确性,因此被广泛地运用在各个领域信号降噪中[17-18]。文章采用小波包降噪方法对含噪的谐波信号进行降噪预处理,降低噪声对VMD算法的影响。 小波包降噪理论依据:含噪信号经过小波包分解后,代表有效信号的小波包分解系数幅值大于噪声的分解系数幅值,选择合适的阈值对有效信号幅值保留,将代表噪声的分解系数幅值设为零,最后重构信号,获得降噪处理后的信号。 小波包降噪的关键在于选取合适阈值,文章选择运用广泛的默认阈值λ,并采用小波软阈值去噪函数进行降噪处理,具体计算公式为: (8) VMD在对谐波信号进行处理时需要预先设定分解个数K。若K取值过小,会使谐波信号欠分解,导致IMF分量信息丢失或者产生模态混叠现象;若K取值过大,会使谐波信号过分解,过分解得到的IMF分量并不是谐波信号中的有效成分,对过分解量进行参数检测将直接导致检测结果错误[19]。 VMD算法通过迭代搜索变分模型的方式来提取每一个IMF分量,在IMF分量的时间域[t-δ,t+δ](δ=2π/ωk(t))上,瞬时频率ωk(t)相较于相位φk(t)的变化是缓慢的,可以认为每个分量都是频率为ωk(t)的谐波信号。 当VMD发生过分解时,其过分解产生的分量是在原分量的基础上分解得到的,过分解的分量特别是在高频,模态分量的瞬时频率发生跳变,信号断裂,断裂处的瞬时频率ωk(t)为0,导致该模态分量的平均瞬时频率降低。基于此,文章提出一种以模态分量瞬时频率均值变化为基础的最优K值选取方法。 假设第i个IMF分量有M个采样点,第j个采样点的瞬时频率为fij,瞬时频率均值如式(9)所示: (9) 式中N为该IMF分量的瞬时频率个数。 谐波信号经VMD分解得到从低频到高频依次排列的模态分量。建立坐标轴,y轴为平均瞬时频率值,x轴为模态序列数,在坐标轴中画出该IMF分量的瞬时频率均值点并用直线连接,当瞬时频率产生跳变时,曲线发生弯折,同时考虑到欠分解的干扰,选取曲线平滑时最大分解模态个数,即为最优分解K值。 算法主要分三部分:第一步,对待测信号进行WPT降噪处理;第二步,将降噪处理后的信号采用VMD预分解,并进行参数K的优化选取;第三步,VMD分解,通过HT进行谐波的参数提取。文中算法框图如图1所示。 图1 算法框图 使用一种典型的负载电流模型,含有谐波的电流信号如式(10)所示: x(t)=100sin(100πt)+40sin(300πt)+ 30sin(500πt)+20sin(700πt)+v(t) (10) 式中第一项为电流的基波成分,频率为50 Hz,幅值为100 A。公式的后三项分别为3次、5次、7次谐波,频率分别为150 Hz、250 Hz、350 Hz,幅值分别为40 A、30 A、20 A。v(t)为加入的高斯白噪声,加入噪声后的信号信噪比为20 dB。 首先,对待检测的电流谐波信号进行WPT降噪处理,信号采样频率为1 000 Hz,采样点数为1 000。取前300个采样点显示,WPT降噪前后的谐波信号波形图如图2所示。 图2 原始信号WPT降噪 由图2可以观察到,信号经WPT去噪预处理后,波形得到了较为明显的改善。 对降噪后的谐波信号进行VMD预处理,并画出模态分量的瞬时频率均值曲线图,图形如图3所示。 由图3可知,当VMD出现了过分解,过分解得到谐波模态分量的瞬时频率发生跳变,导致瞬时频率均值曲线图发生弯折。由于欠分解导致的模态混叠问题,K为2时曲线平滑,且K为3时曲线仅存微小的弯折,为避免欠分解对K值选取的干扰,选择曲线平滑时对应的最大K值即可。 谐波信号存在四个谐波分量,由VMD算法对分解得到的IMF分量定义可知,最优的分解模态个数为4,观察图3发现,曲线平滑时最大K值为4。选择K=4为最优参数,分别对原始信号与降噪预处理后的信号进行VMD分解,分解结果如图4、图5所示。 图3 IMF分量瞬时频率均值变化 图4 原始信号VMD分解结果 图5 去噪信号VMD分解结果 观察图4、图5,原始信号经VMD分解得到IMF分量受到噪声干扰,波形发生了严重畸变。对谐波信号进行降噪预处理并利用VMD分解所得到的IMF分量受到干扰较小,有利于后续谐波参数提取。 利用VMD算法直接提取IMF分量的频率,希尔伯特变换检测IMF分量的幅值。频率、幅值检测结果分别如表1、表2所示。 表1 频率检测结果 表2 幅值检测结果 由表1、表2可知,频率检测方面,文章在150 Hz、250 Hz、350 Hz时的检测误差分别为0.011%、0.016%、0.012%,显然文中在高频检测上拥有较好的检测精度。幅值检测方面,文章算法降低了噪声的影响,在100 A与40 A时的检测误差为0.270%与0.522%,幅值检测结果较为精确。谐波参数检测结果表明文章提出的算法能够有效地抑制噪声的影响并选取VMD分解的最优K值,保障后续谐波参数测量的准确性。 采用RIGOLDG4062波形发生器设置相关参数产生1次、3次、5次谐波,幅值分别为2.5 V、0.632 V、0.632 V,频率为50 Hz、150 Hz、250 Hz,将波形发生器的输出端与Tektronix MDO3024示波器相连接,U盘与Tektronix MDO3024示波器的USB接口相接采集数据,并在其中加入一定的噪声,波形图如图6所示。 图6 采集信号波形图 对采集到的信号做WPT降噪预处理,降噪后的信号波形图如图7所示。 图7 去噪后采集信号波形图 利用瞬时频率均值法确定最优的VMD分解模态个数K,瞬时频率均值曲线变化如图8所示。 图8 瞬时频率均值变化 由图8可知,选取K=3作为VMD最优分解个数,对降噪后信号进行VMD最优分解,分解结果如图9所示。 图9 VMD分解结果 利用VMD算法直接提取频率,HT算法提取IMF分量的幅值,实现谐波参数检测。检测结果如表3所示。 表3 谐波检测结果 由表3可知,文章算法在高频检测中具有较好的检测精度,150 Hz与250 Hz的检测误差为0.03%与0.02%。幅值检测方面,三个谐波成分的幅值检测误差均在1%以下。实验数据的检测结果验证了文中算法的有效性, 且具有较好的检测精度。 VMD算法谐波检测是针对EMD算法在谐波测量中存在问题提出的一种新的算法。VMD算法分解结果与EMD分解结果类似,但VMD算法分解模态个数K选择合适能够克服模态混叠问题。 文献[10]采用CEEMDAN方法进行谐波检测,CEEMDAN算法是一种改进的EMD算法,在谐波检测中同样能够有效的抑制噪声的干扰,克服模态混叠问题。采用文献[20]中的系统模型和参数,用文中方法参数测量得到的检测结果和文献[20]得到的测量结果进行比较,结果如表4、表5所示。 表4 频率检测结果 表5 幅值检测结果 从表4和表5观察可知,频率检测方面,文中算法在低频与高频的检测精度均高于文献[20]的检测精度,尤其在150 Hz与250 Hz检测中,文中算法的检测结果更加接近原始数据。幅值检测方面,文章在5.4 V与10 V的检测误差要低于文献方法的检测误差。综合评价,文章算法在谐波参数检测中要优于文献[20]的检测算法。 文章提出一种WPT-K值优化的VMD算法模型,采用WPT降低噪声对VMD分解影响,并根据VMD算法自身分解特点,通过解析分量瞬时频率均值变化曲线进行最优模态分解数K选取,实现信号最优K值VMD分解。 将文章算法应用于含噪的谐波信号检测中,仿真与比较结果验证了算法的有效性,且参数检测结果更加精确。2 WPT-K值优化VMD谐波检测方法
2.1 小波包降噪
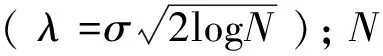
2.2 K值优化
2.3 算法步骤
3 谐波检测
3.1 算法仿真
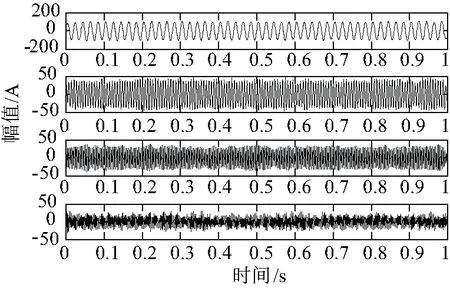
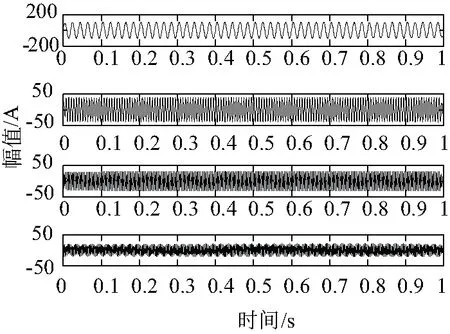
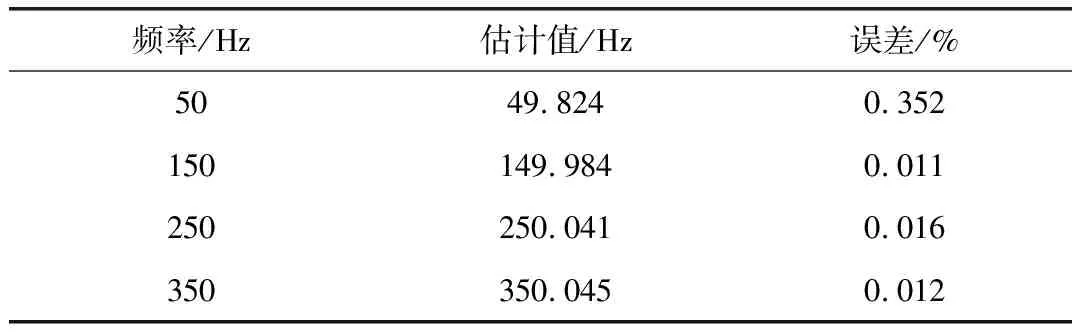
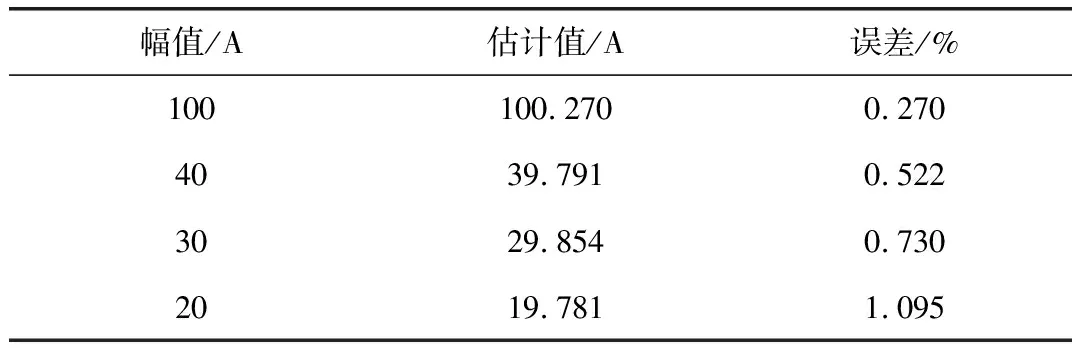
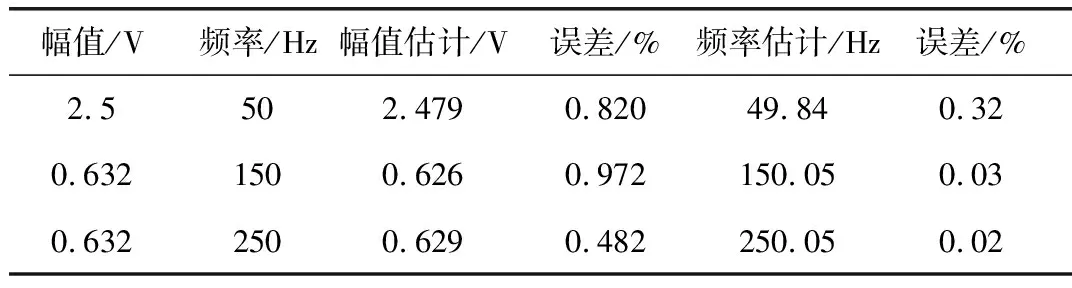
3.2 实验数据处理
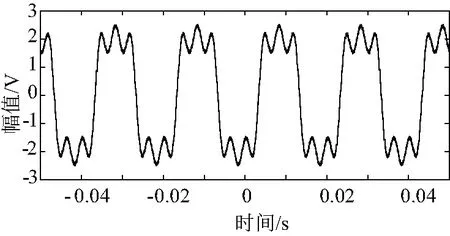
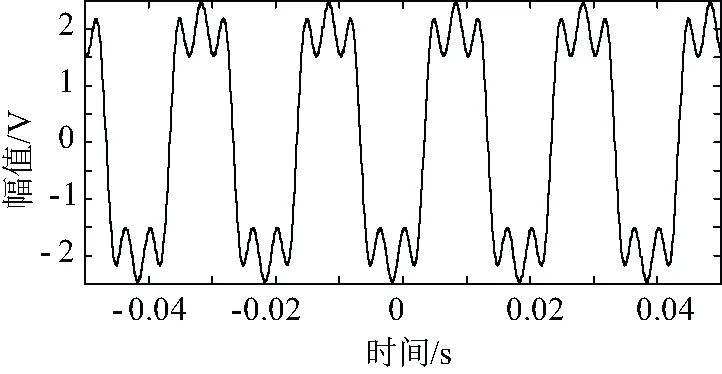
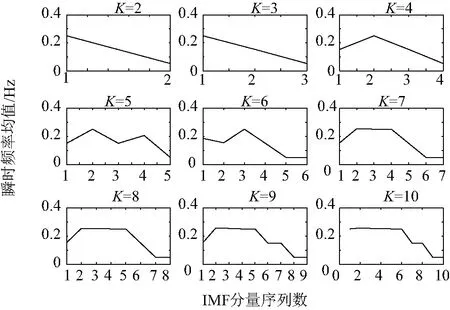
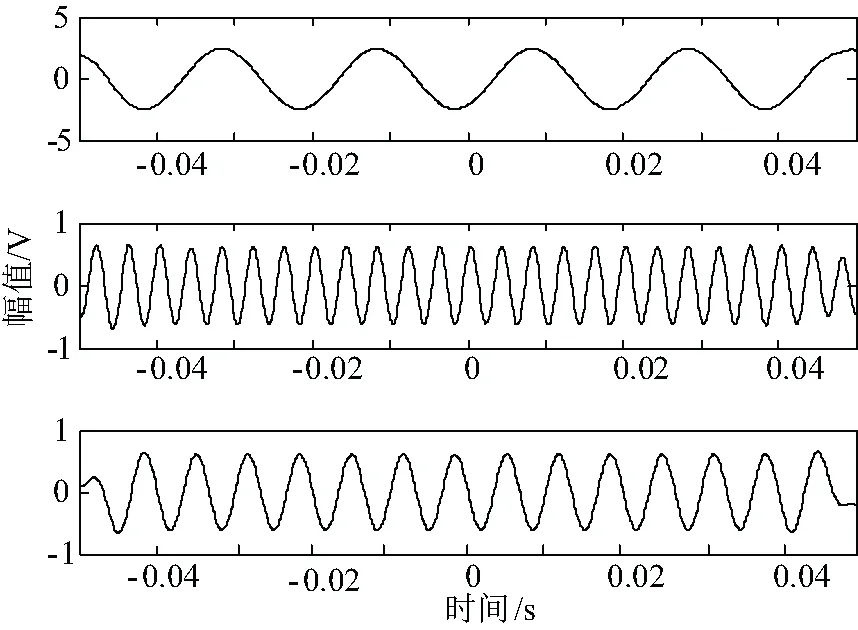
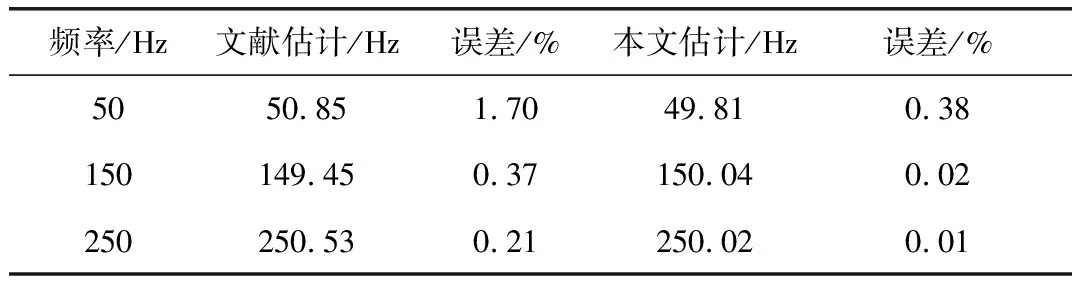
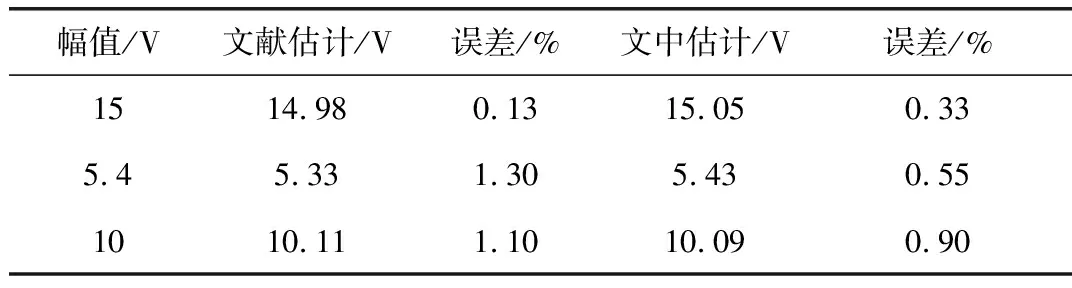
3.3 算法比较
4 结束语

