基于线性化潮流的安全约束机组组合方法

岑海凤，许苑，李涛，陈坤, 郑温剑，李志刚

(1.广东电网公司广州供电局，广州 510620； 2.华南理工大学 电力学院，广州 510640)

0 引 言

机组组合(Unit Commitment, UC)是电力系统短期发电调度的重要任务之一。在UC问题中，一般将减少系统发电成本作为优化目标，在满足负荷需求、备用需求等约束条件的前提下，确定各时段各机组的启停状态和出力大小。安全约束机组组合(Security-Constrained Unit Commitment，SCUC)进一步考虑了系统基态与预想故障下的网络安全约束，可提高发电计划的安全性[1]。为了改善求解效率，通常可将SCUC问题分解为UC主问题与网络安全校验子问题来处理[2]。

由于考虑了潮流方程，UC在数学上是一个非凸的混合整数非线性规划问题，求解十分困难。直流潮流(DC Power Flow, DCPF)模型是目前UC广泛采用的模型[3-5]。它针对UC非凸性的来源，对潮流等式约束进行了线性近似，计算效率高，但难以将其应用于与电压、无功相关的研究领域。且当线路电阻电抗比R/X比较大或网络电压偏离额定值比较大时，DCPF模型所得到的结果误差大[6]。针对DCPF模型的不足，许多学者对考虑了交流潮流(AC Power Flow, ACPF)约束的UC进行了研究[7-8]。但因为问题本身的非凸性，目前所采用的方法难以求得全局最优解，不能保证求解的质量。而随着凸优化理论的发展，出现了将潮流等式约束进行凸松弛处理，从而转换为凸优化问题求解的方法[9]。该方法可以保证求解的质量，但在松弛不精确的情况下，其所得到的解没有实际物理意义。针对DCPF模型的不足与应用ACPF的局限性，不少学者对考虑了电压与无功的线性化潮流模型进行了研究[10-11]。线性化潮流模型基于泰勒级数展开等数学变换，可以准确地逼近ACPF，目前已在最优潮流问题中得到了应用[12-13]。

线路潮流与节点电压在N-1条件下的安全校核是最为常见的网络安全校验问题[14-15]。为了掌握N-1线路开断后的系统状态，通常可以利用支路开断分布系数 (Line Outage Distribution Factor，LODF)[16-17]或灵敏度分析法[18]来计算。LODF以DCPF模型为基础，凭借其可通过基态断线线路的有功潮流计算故障后网络的有功潮流分布。但是LODF同样不能计算故障后的电压与无功分布。而灵敏度分析法虽然可提供节点电压、线路有功和无功潮流等全面的运行数据，但其中的灵敏度系数与系统故障前的运行状态有关，难以应用于UC问题中。针对上述问题，文中提出了一种可计算故障后的电压和无功分布、仅与网络结构相关的改进支路开断分布系数(Modified Line Outage Distribution Factors，MLODF)。文中主要创新点如下：

(1) 文中对于一种线性化潮流模型，推导了其对应的MLODF。利用该MLODF可准确逼近线路断线后系统的节点电压、线路有功和无功分布；

(2)文中提出了一种基于MLODF的SCUC模型，该模型较传统基于LODF的模型可提供更为安全的发电计划。

文中首先对MLODF进行了推导；接着描述了基于MLODF的SCUC模型；然后介绍了模型的求解方法；最后通过算例分析说明所提出模型的性能。

1 MLODF的推导

对于一种线性化潮流模型，这节展示了其对应MLODF的推导过程。

在静态安全分析中，通常使用灵敏度分析法对线路开断的场景进行模拟。灵敏度分析法将支路开断视为正常运行情况下的一种扰动，通过节点注入功率的变化量来模拟线路开断的影响。图1对支路nm开断的场景进行了模拟。

如图1(a)、图1(b)所示，线路开断前、后应满足的功率平衡方程式分别为式(1)、式(2)：

(1)

(2)

如图1(c)所示，模拟线路开断时，假设除断线线路外，其余线路潮流应与断线后的潮流一致。此时列写节点功率平衡方程式有：

(3)

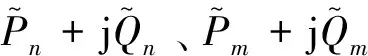
将式(3)减去式(2)可得：

(4)

式中ΔPn+jΔQn、ΔPm+jΔQm分别为模拟线路开断前后节点n、m的注入功率变化量。

在文献[10]中，采用了下列线性表达式来逼近支路潮流：

Pij=gij(Vi-Vj)-bij(θi-θj)

(5)

Qij=-bij(Vi-Vj)-gij(θi-θj)

(6)

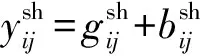
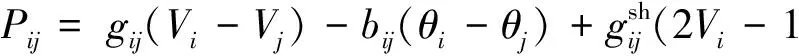
(7)

(8)

整合式(7)和式(8)，可得到节点注入功率的表达式：

(9)

式中Y=G+jB为节点导纳矩阵；Y=G+jB为不包含并联元件的节点导纳矩阵；Ysh=Gsh+jBsh表示节点并联元件向量。

通过对式(9)执行一阶泰勒级数展开，可以计算节点注入功率与节点电压间的灵敏度系数：

(10)

在模拟线路nm开断时，当给定节点注入功率变化量ΔP、ΔQ时，可以通过灵敏度系数求解节点电压变化量ΔV、Δθ：

(11)

其中：

(12)

根(11)，可以计算节点n、m的电压变化量：

(13)

整合(7)、式(8)和式(13)，可以得到故障前线路nm潮流、故障后线路nm潮流以及故障前后节点n、m注入功率变化量：

(14)

将式(4)带入式(14)得：

(15)

根据式(11)和式(15)，可通过故障前线路nm潮流计算故障前后各节点电压的变化量：

(16)

定义αi,nm、βi,nm、εi,nm、γi,nm为故障前线路nm的潮流与故障前后节点i电压变化量间的灵敏度系数。因此可将故障后节点i的电压表示为：

(17)

(18)

此外，故障后线路ij的潮流可表示为：

(19)

其中：

(20)

类似地，ΔQij、ΔPji、ΔQji也能通过故障前线路nm的潮流计算得到。

2 SCUC的数学模型

2.1 优化目标

文中SCUC的优化目标是最小化系统的发电成本。而火电机组的发电成本可用下列线性函数来描述：

(21)

2.2 约束条件

(1)节点功率平衡约束

(22)

(23)

(2)旋转备用约束

(24)

(25)

(26)

rdg,t-pg,t≤0

(27)

(28)

(3)爬坡约束

-RDg≤pg,t-pg,t-1≤RUg

(29)

式中RUg和RDg为单个时段中机组的爬坡容量与滑坡容量。

(4)机组状态变量间的逻辑约束

ug,t-ug,t-1=xg,t-gg,t

(30)

(31)

(32)

ug,t∈{0,1},0≤xg,t≤1,0≤yg,t≤1

(33)

其中，MDg为机组最小停机时间。

(5) 无功出力约束

(34)

(6)基态网络安全约束

(35)

(36)

(7) N-1网络安全约束：

(37)

(38)

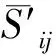
3 模型的求解

由于电力网络中线路众多，需要考虑的N-1安全约束数目也很多。然而绝大多数的N-1安全约束是不起作用约束，可以在优化模型中忽略。为了减少处理的N-1安全约束数目，文中借鉴了文献[3]的方法，通过反复校验添加的方式来处理N-1安全约束。具体流程图如图2所示。

图2 处理N-1安全约束的流程图

首先求解基态的UC问题，意味着需要将约束式(22)～式(36)加入至模型中。根据求解结果，可以得到基态下的线路潮流和节点电压。然后，可通过式(37)利用MLODF计算各条线路断线后的网络潮流。接着，对所有N-1故障进行安全校验，若所有故障后的线路潮流和节点电压均满足式(38)，则说明目前的UC结果能够满足N-1准则，得到了最终解；若不满足，则需要以式(37)、式(38)的形式将相应的线路约束和电压约束加入至模型中求解。而求解完包含N-1安全约束的SCUC问题后，还需根据式(37)重新分析故障后的网络潮流，以判断是否有额外的N-1约束需要加入求解的模型中。就这样通过反复地校验、添加约束，直至得到的解满足所有N-1安全校验为止。

4 算例分析

文中SCUC的调度周期为24 h。这节首先对6个测试系统进行N-1故障分析来说明MLODF的准确性；接着对比了6节点系统和118节点系统中不同模型的SCUC结果的安全性；最后通过分析118节点系统中的SCUC结果来说明所提出模型的安全性。

文中采用了文献[13]的方法将约束式(36)和式(38)线性化，从而将SCUC转化为混合整数线性规划问题。所有的优化问题通过在软件MATLAB R2018a上调用求解器Gurobi 8.1.1[20]来求解。

4.1 MLODF准确性分析

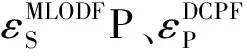
表1 不同线性化潮流模型的误差

假设DCPF模型的电压幅值均为额定电压。

由表1可以看出，MLODF与ACPF的电压、有功潮流的误差均小于DCPF。因为MLODF在DCPF的基础上考虑了电压与无功的影响，因此其对ACPF的近似效果更好。此外，从表1中的第4列和第7列可以看出，MLODF 与原始线性化潮流模型的误差数量级大致为1e-15。这体现了文中MLODF推导过程的正确性。

4.2 MLODF与LODF的安全性对比

为了说明文中提出的基于MLODF的模型(M1)较传统基于LODF的模型(M2)的优越性，本节对6节点系统和118节点系统进行了测试，对比了两种模型的SCUC结果。

6节点系统包含了3台发电机与7条输电线路。系统的线路参数、发电机特性数据和负荷数据均取自文献[19]。网络结构图如图3所示。

图3 6节点系统网络结构图

图4展示了M1模型和M2模型的SCUC中各机组的启停状态。其中前者的发电成本为111 328.590$，后者的为109 560.502$。

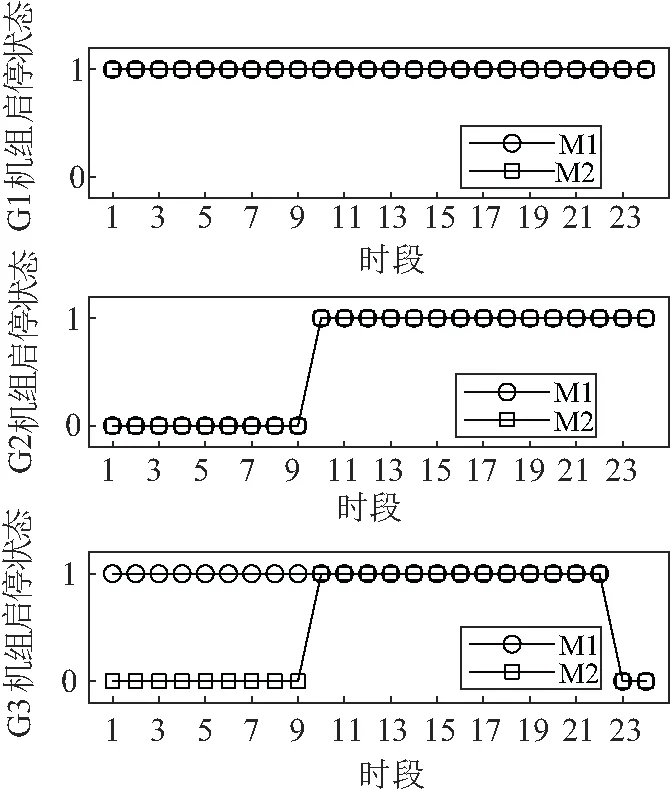
图4 6节点系统各机组的启停状态

由图4可看出，当使用M2模型时，G3机组在1-9时段内没有启动。这主要是由于以下两个原因引起的：(1) M2模型没有考虑无功功率平衡约束。G1机组的无功出力上限为50 Mvar，而对于时段1、8和9，系统总的无功负荷分别为50.37 Mvar、51.06 Mvar和53.71 Mvar。为了满足系统的无功需求，采用M1模型时会在相应时刻启动较为便宜的G3机组与G1机组一同承担负荷;(2) M2模型没有考虑系统可能发生的电压越限问题。对于时段2-7，当仅有G1机组启动时，若线路1-2发生断线，此时节点2的电压往往会低于电压下限值。此时需启动G3机组来改善网络的功率分布以提高节点2的电压。

为了进一步说明M1模型较M2模型的安全性，下文对118节点系统进行了测试。118节点系统包含了54台发电机与186条输电线路。系统的线路参数、发电机特性数据和负荷数据均取自文献[19]。图5展示了基于M1模型和基于M2模型的SCUC中各机组的启动时段。其中前者的发电成本为803 693.693$，后者的为794 533.039$。

图5 118节点系统各机组的启动时段

由图5可以看出，M1模型较M2模型需额外启动4台机组，它们分别为连接在节点8的3号机组、连接在节点32的14号机组、连接在节点36的16号机组和连接在节点59的24号机组。当不启动3号机组时，基态下线路8-5为无功重载线路。当线路8-5开断后，故障前线路上的潮流主要往短线路8-30转移，这会造成线路8-30视在功率过载。此时通过启动3号机组可以改善网络潮流分布。若14号与16号机组总处于停机状态时，随着网络无功负荷的增加，部分时段中节点31和节点39、节点40的电压会低于下限值。因此M1模型会在相应时段启动这两个机组以提高附近节点的电压。此外，由于在8-24时段仅启动21号机组不能满足节点59的无功负荷需求，因此M1模型会在相应时段启动24号机组来承担无功负荷。

从上述两个算例可以看出，由于M1模型考虑了电压和无功分布，基于M1模型的SCUC结果可解决潜在的电压越限和视在功率越限问题。因此较传统的M2模型，M1模型可提供更为安全的发电计划。

4.3 MLODF安全性分析

为了探究基于MLODF的SCUC结果对于实际N-1线路开断故障的承受能力，这节对118节点系统进行了测试。仿真时将SCUC结果中的相关变量(PQ节点的注入功率、Vθ节点的电压和 PV节点的电压幅值和有功注入功率)固定后进行ACPF计算，分析了线路开断后的系统状态。

将SCUC结果在线路N-1故障下进行ACPF校验，发现有48处线路潮流越限(在所有N-1故障中占比为0.518%)、有152处节点电压越限(在所有N-1故障中占比为1.224%)。其中线路潮流越限的情况主要发生在线路65-68开断时，线路47-69与线路49-69的潮流发生越限。电压越限的情况主要有两种。一种发生在线路37-39开断时，节点39与节点40的电压低于下限值；另一种发生在线路100-103开断时，节点110、111与112的电压低于下限值。对越限情况的严重程度进行分析，计算得到的平均潮流越限量为10.177 MV·A(占线路视在功率容量的5.356%)、平均电压越限量为0.023 2 p.u.。由于越限量大，此时SCUC结果不能在这些故障发生时保障系统的安全性。而对于其他98%以上的N-1故障，SCUC结果可以保障线路潮流和节点电压在安全的限值之内。因此基于MLODF的SCUC结果能在绝大多数N-1故障下保障系统的安全性。

为了进一步分析严重故障对于模型准确度的影响，图6～图8展示了在峰荷时段17、对电压与线路潮流准确度影响最大的断线场景下的网络潮流分布。由图6可以看出，此时节点39和节点40发生了电压越限。这是由于当线路37-39开断后，节点39和节点40上的无功负荷不能通过近距离的连接在36号节点上的机组直接承担，从而引发了节点电压下降。在图中可观察到此时的节点电压已经偏离额定电压，即偏离了近似时的假设条件，从而导致了误差的增大。而从图7可看出，即使在严重故障场景下，该模型仍对线路有功功率保持了良好的逼近效果。由图8可以看出，此时105号线路47-69与106号线路49-69发生了潮流越限。这主要是因为此时模型对线路无功功率近似效果差造成的。线路47-69与线路49-69均为长线路，支路电抗大。当线路65-68开断时，连接在节点49、节点69的发电机组均处于启动状态。此时节点49、节点69电压分别为0.959 p.u.和1.012 p.u.，而节点47与节点49相连，作为负荷节点，其电压要低于节点49。由于线路47-69与线路49-69电抗大、电压差值大，所以线路的无功损耗大。通过式(7)和式(8)可知，文中所采用的线性化潮流模型忽略了支路损耗。所以此时模型对相关线路无功功率的逼近效果差，从而导致了其与相关线路视在功率间的误差增大。

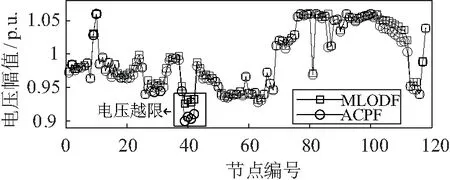
图6 时段17线路37-39开断时系统电压分布

图7 时段17线路65-68开断时系统有功功率分布

图8 时段17线路65-68开断时系统视在功率分布

从上述的分析可以看出，少数N-1故障在交流潮流校验下发生越限是由于节点电压偏离额定电压或线路无功损耗增大造成的。在这些故障情景下，实际的网络潮流偏离了线性化潮流模型节点电压为额定电压、忽略支路损耗的假设，因此此时模型误差变大，进一步导致了交流潮流校验越限。

5 结束语

文中针对一种线性化潮流模型推导了与之对应的MLODF，并将MLODF应用到了SCUC中。算例的结果表明：

(1)MLODF较DCPF对ACPF的近似效果更好。此外，它保持了原有线性化潮流模型的精度，这说明了推导过程的正确性；

(2)基于MLODF的SCUC模型考虑了无功和电压约束。较传统基于LODF的模型，它能提供更为安全的发电计划；

(3)对于绝大多数N-1故障，基于MLODF的SCUC结果可以保障线路潮流和节点电压在安全的限值之内。

需要指出，部分线路开断时，可能会出现系统电压偏离额定值或线路无功损耗过大的情况。此时MLODF模型的精度降低，得到的SCUC结果不够理想。因此，下一步的工作内容主要在于如何进一步地提高模型的准确度。