电网电压骤升时DFIG定子磁链暂态全过程及其影响因素研究

孙丽玲，尹思杰，王艳娟

(1.华北电力大学 电气与电子工程学院，河北 保定 071003； 2.国网冀北电力有限公司，河北 唐山 063299)

0 引 言

随着能源需求增加，风电开发成本进一步降低。在能源消费结构中风电的角色日益重要。根据“十三五”的计划部署，截止至2020年，风电的总装机容量应不低于2.1亿千瓦[1-2]，在国际上风电装备技术和创新能力达到先进水平。随着风电装机并网容量快速增加，系统稳定性很大程度上与风电机组运行稳定性密切相关。其中，故障穿越运行属于难度比较大，要求比较高的。低电压穿越技术已经有了一定的研究成果，比较成熟。相比较而言，电网异常现象中较常见的高电压穿越(High Voltage Ride-Through，HVRT)故障的重视程度远逊于低电压穿越[3-9]。与此同时，我国目前的高电压穿越准则尚未明确。国际上，澳大利亚已经率先制定了正式的相关并网准则，在电网电压骤升至1.3 p.u.时，风电机组不脱网运行的最短时长应不低于60 ms，且故障恢复电流应该足够大[10-13]。

双馈感应风力发电机(Doubly Fed Induction Generator，DFIG)有着很多优点，诸如换流器容量小，调速范围宽，有功无功解耦控制等，因此双馈感应风力发电机大量应用于风电系统中。DFIG高电压穿越问题中，电压上升和恢复期间都会激起不同程度的电磁暂态过程，其中定子磁链瞬态特性是造成转子过电压和过电流的主要原因，对其进行研究是实现高电压穿越运行的基础和依据。

大量文献都研究了电压故障时的定子磁链ψs瞬态特性。文献[14]对不计线路阻抗影响情况下的ψs的瞬态特性，得出故障切除时，DFIG的ψs中无瞬态分量存在；文献[15]对DFIG的ψs特性进行了精确的分析和计算，得出ψs瞬态衰减分量的本质变化规律，给出未采取任何近似及省略情况下的ψs表达式，但没有提及故障切除后ψs的变化规律；文献[16]研究了电压下降时ψs的暂态全过程，但并未对不同模式下的电压故障进行研究；文献[17]对HVRT下的DFIG行为进行了分析，为实现故障期间DFIG定子端电压不变以此来抑制ψs瞬态衰减分量，提出串联网侧换流器GSC(Grid Side Conventer，GSC)的控制策略；文献[18-19]用运解析法深入地分析了故障时DFIG的过渡过程，得出ψs解析式；文献[20]针对DFIG的HVRT问题，对比分析了DFIG低电压和高电压期间的电磁暂态特性。

但以上文献只对电网电压单一故障模式下ψs瞬态特性进行分析，而未考虑故障恢复后ψs的动态变化，对DFIG的ψs瞬态特性分析不全面。针对以上不足，文中对电压不同骤升模式下的定子磁链瞬态全过程进行了研究，对比分析了影响ψs特性的因素。电网电压骤升模式不同，ψs的暂态特性也不同，且模式I的暂态衰减分量远大于模式II；相邻两次电压上升幅度相同，且时间间隔为Δt=(n+0.5)Ts时，能够最小化ψs的暂态衰减分量。理论分析通过仿真进行了验证，针对DFIG的动态过程分析，文章具有一定的参考价值，为制定DFIG高电压穿越控制策略提供了理论参考。

1 DFIG暂态全过程分析

研究DFIG在电压不同上升模式下的ψs暂态特性，依照电动机惯例，在两相静止αβ坐标系下：

(1)

(2)

其中，电压、电流、磁链矢量用U、I、ψ表示，电阻和电感用R、L表示，定、转子间互感Lm表示，转子旋转角速度ωr表示，下标s、r表示定、转子分量。

忽略定子电阻Rs，由 ：

(3)

其中转子旋转角速度为ω1。假设电压突变前后Us为：

(4)

式中t0为电网电压骤升故障发生时间；t1为电网电压骤升故障恢复时间，电压突变会导致电磁暂态过渡过程，其中ψs不能突变，此时的ψs由ψsf和ψsn组成；稳态分量ψsf以同步角速度旋转，幅值与Us成正比，由式(3)、式(4)可知ψs瞬态全过程中的稳态分量ψsf为：

(5)

式中ψsn是为保证ψs连续产生的；ψsn是以ψs衰减时间常数τs=Ls/Lr按指数规律变化的分量。由换路定理ψs(t-)=ψs(t+)，可得ψsn的幅值为：

(6)

对于兆瓦级DFIG，相邻两次电网电压故障的时间间隔Δt=t1-t0与定子时间常数τs相比是很小的，因此上式中e-(t1-t0)/τs可忽略不计，电压故障后ψsn的幅值简化为：

(7)

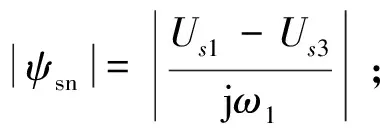
由式(5)、式(7)可知，电压在不同骤升模式下ψs的瞬态全过程为：

ψs=

(8)

2 ψs瞬态特性影响因素

由上一节可以得出，电压骤升幅度和连续两次变化的时间间隔会对ψs暂态特性造成影响。分析影响ψs的因素能够合理调整时间间隔和电压骤升幅度，通过降低ψsn的大小，有利于实现高电压穿越。

图1给出了t=t0时电压上升，t=t1时电压恢复下的ψs轨迹：若Δt=nTs，则故障前的运行轨道c1和故障回复后的运行轨道c2一样；若Δt=(n+0.5)Ts，则故障前的运行轨道c1和故障回复后的运行轨道c2不一样，c2为图中所示更大的圆。

故障前，ψs运行于以点A(0，-1)为圆心的圆，t=t0时电压骤升，ψsn的存在使其从稳态过渡到高电压条件下新的运行轨迹c1。电压恢复时，若Δt=t1-t0=nTs，即A点恢复，ψs的运行轨迹再次回到A点，暂态衰减分量为零；若Δt=t1-t0=(n+0.5)Ts，即电压在B点恢复，此时，ψsn为电压骤升时的2倍，ψs的运行轨迹将变为一个较大的圆c2。

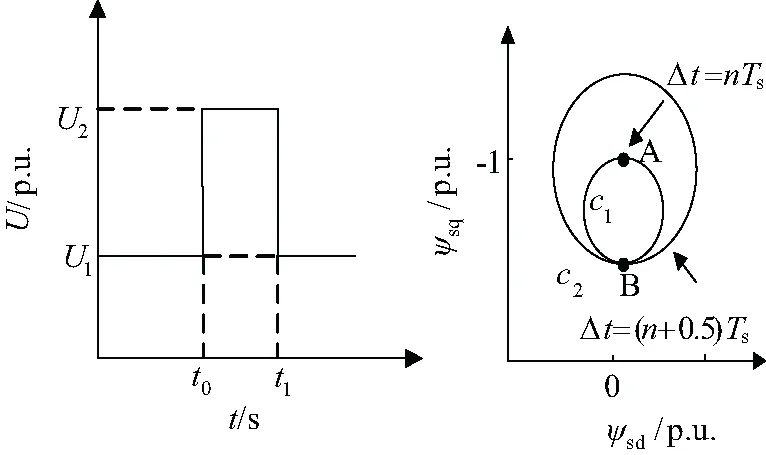
图1 DFIG的ψs运行轨迹

此外，电压骤升模式不同，ψs变化规律也不同。图2对比给出了不同电压骤升模式及相邻两次电压变化时间间隔对ψs瞬态特性的影响规律。

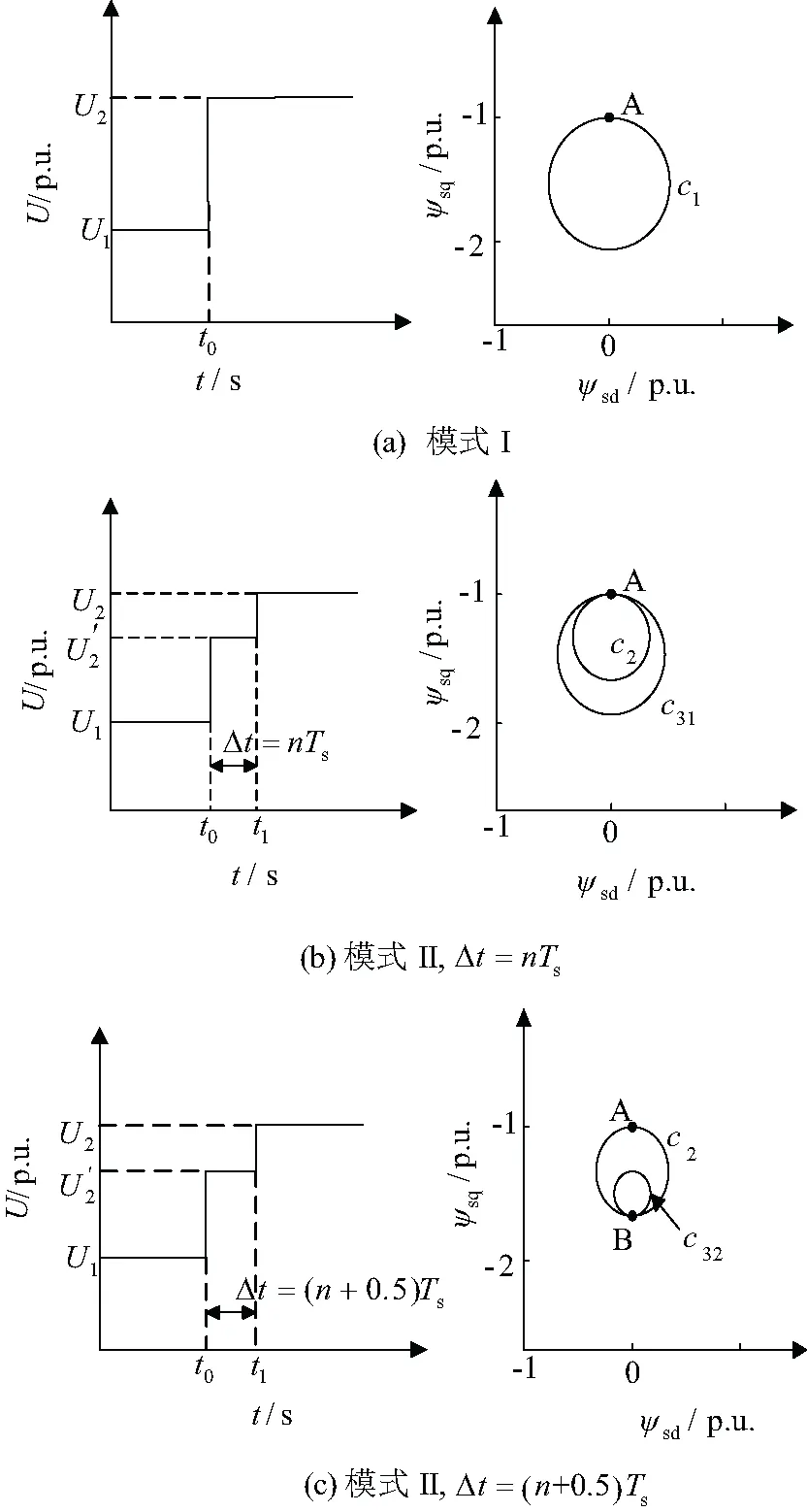
图2 不同模式下ψs运行轨迹

对于模式I，t=t0时，电压由U1直接上升至U2，此时c1为ψs的运行轨迹，如图2(a)所示。对于模式II，t=t0时，电压由U1上升至U′2，t=t1时，电压继续上升至U2。电压上升至U′2后，ψs的运行轨迹为c2，且c2的半径明显小于c1；若Δt=t1-t0=nTs，即电压于A点继续上升至U2，ψs运行轨迹变化为c31，如图2(b)所示；若Δt=t1-t0=(n+0.5)Ts，即电网电压在B点继续骤升至U2，此时定子磁链运行轨迹变化为c32,如图2(c)所示。通过以上可以得出，电压上升模式不同，ψs的运行轨迹也不同。模式I下ψsn的幅值远大于模式II，且连续两次电网电压变化时间间隔为Δt=(n+0.5)Ts时，电压上升后，ψsn分量的幅值更小。

图3给出模式II下，且Δt=(n+0.5)Ts时，不同电压上升幅度对ψs瞬态特性的影响规律。若U′2-U1=U2-U′2，即电压在B点继续骤升至U2，此时ψs运行轨迹稳定于该点，定子磁链暂态衰减分量为0；若U′2-U1>U2-U′2，如图2(c)所示，即电压在B点骤升至U2后ψs运行轨迹为c32。因此，若相邻两次电压上升幅度相同，ψsn的幅值更小。

图3 电压骤升幅度对ψs影响

电压骤升与电压恢复互为逆过程，对电压恢复过程的研究同样可分为两种模式对其进行研究。电网电压的恢复过程与电网电压骤升有着一致的变化规律，此处不再赘述。

通过对不同骤升模式时电网电压骤升幅度和时间间隔对ψs暂态特性的影响分析可知，两次连续电网电压变化的时间间隔为Δt=(n+0.5)Ts，且相邻的两次骤升幅度相同时，能够最小化ψsn的幅值。可以得出，通过有效控制电压的时间间隔与骤升幅度，可以降低ψsn的幅值，有利于高电压穿越的实现。

3 仿真分析与验证

为验证上述ψs暂态特性的正确性，利用MATLAB/Simulink仿真平台，构造DFIG仿真模型，如图4所示。其中转子侧换流器(RSC)和网侧换流器(GSC)构成DFIG的背靠背换流器，其中RSC的主要作用是：实现恒频恒压和DFIG的有功功率和无功功率的独立调节。GSC的主要作用是:保持直流母线电压的稳定和实现电网侧无功功率控制。其中双馈感应发电机参数为：额定功率为2 MW，稳定频率为50 Hz，定子额定电压为690 V，直流母线额定电压为1 200 V，定子电阻为0.010 8 p.u.，转子电阻为0.010 2 p.u.，定子漏感为0.102 p.u.，转子漏感为0.11 p.u.，定转子间互感为3.362 p.u.。由于兆瓦级DFIG转动惯量较大，且电网电压骤升暂态过程较短，因此在整个过程中可以认为DFIG转速不变。

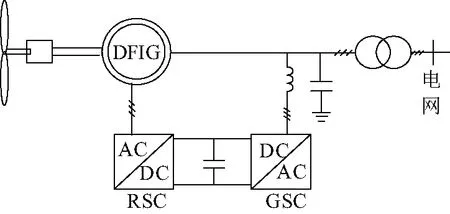
图4 DFIG仿真模型

图5给出了电网电压骤升至1.3 p.u.，t0=1 s,t1=1.1 s和t1=1.11 s时(即相邻两次故障时间间隔分别为Δt=5Ts和Δt=5.5Ts)电网电压恢复的定子磁链运行轨迹图。

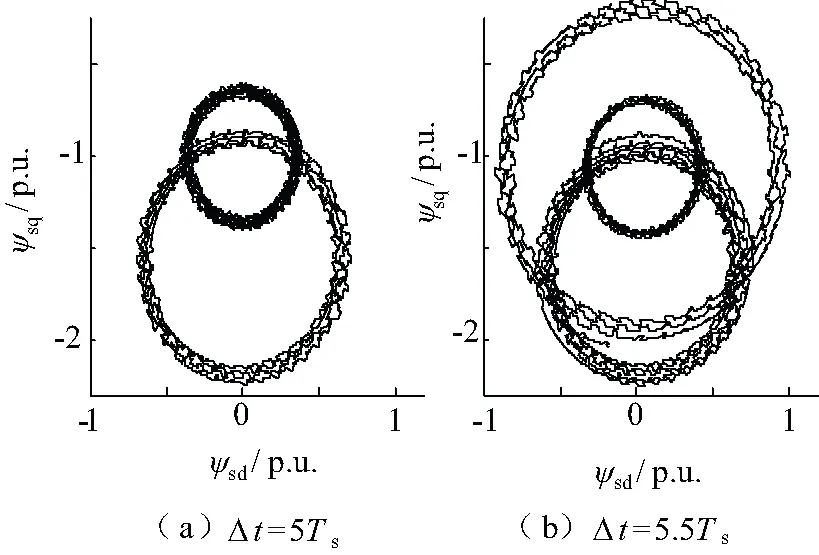
图5 定子磁链运行轨迹

由图5(a)、图5(b)可知，在电压骤升前，定子磁链以点(0,-1)为圆心的圆内运行。电压上升后，由于ψsn的作用，使得定子磁链从一个稳态变化到高电压条件下新的稳态，其圆的半径逐渐扩大。在电压恢复过程中，相邻的两次故障时间间隔不同，ψs运行轨迹也不同，若Δt=5Ts，电压恢复后，ψsn为零，ψs轨迹与故障前相同；若Δt=5.5Ts，ψs的振荡幅度将会达到电网电压上升时的两倍，此时ψs逐渐衰减为两倍于故障期间的圆，直至进入稳态。验证了图1理论分析的正确性。

图6给出了模式II下，t0=1 s时电压上升至1.2 p.u.，t1=1.1 s和t1=1.11 s时(即相邻两次故障时间间隔分别为Δt=5Ts和Δt=5.5Ts)电压继续上升至1.3 p.u.时的ψs行轨迹图。

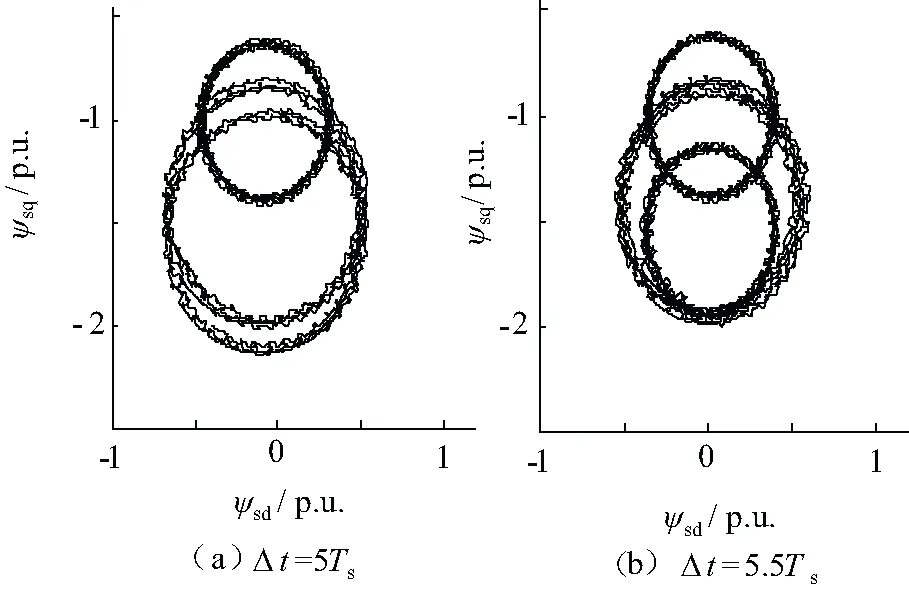
图6 定子磁链运行轨迹

由图6(a)、图6(b)可以看出，ψs的运行轨迹在t1时刻前是完全一样的，当电压第二次上升后，若Δt=5Ts，ψsn增加，定子磁链运行轨迹变成为一个半径更大的圆；若Δt=5.5Ts，ψsn将会减小，定子磁链运行轨迹变化到一个较小的圆。从而验证了图2的理论分析的科学性，也就是当连续的两次电网电压变化的时间间隔为Δt=(n+0.5)Ts时，电网电压上升后ψs的暂态衰减分量的幅值较小。

图7给出了模式II下，t0=1 s时电压上升至1.15p.u.，t1=1.11 s时(即相邻两次故障时间间隔为Δt=5.5Ts)电压继续上升至1.3 p.u.时ψs的运行轨迹图。

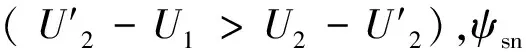
图7 定子磁链运行轨迹

4 结束语

文章研究了不同电压骤升模式下ψs暂态全过程，以此为基础，对比分析了影响ψs暂态特性的因素，得到下列结论：

(1)电网电压骤升模式不同，ψs的暂态特性也就不一样，且模式I的定子磁链暂态衰减分量远大于模式II；

(2)相邻两次的电网电压变化时间间隔为Δt=(n+0.5)Ts时，电压上升后ψsn较时间间隔为Δt=nTs时更小；

(3)相邻两次电压的上升幅度相同时，可以将ψsn的幅值最小化。

如果能够合理控制电网电压的骤升幅度和时间间隔，将利于降低ψsn的幅值。可制定利用这一特点的控制策略，优化HVRT的暂态性能。文章的研究内容对掌握DFIG的动态过程有一定的参考意义，能够从理论层面支撑HVRT控制策略的制定。