基于NS-APSO算法的变压器局部放电超声定位方法

周晶，罗日成，黄军，梁新福，党世轩

(长沙理工大学 电气与信息工程学院， 长沙 410004)

0 引 言

电力变压器作为电力系统中重要的输变电设备，保证其正常运行是提高电力系统安全、稳定性的前提。变压器一旦出现故障会影响区域供电可靠性，造成停电事故的发生。影响变压器正常运行的众多故障中，绝缘故障是最主要的一种[1]。油浸式变压器出现绝缘故障主要是由于其内部的绝缘发生劣化与老化，而局部放电又是造成设备出现绝缘劣化的主要原因[2-3]。因此，如果能在变压器发生绝缘故障之前对局部放电进行检测与定位，就能大大降低绝缘故障发生的概率，提高系统运行的可靠性。

大型电力变压器内部发生局部放电时，将产生一系列的物理和化学现象，局部放电过程中产生的超声波、电脉冲等信号为局部放电的检测和定位提供了多种方法[4]。文献[5]通过检测局部放电产生的超声波信号并利用RSS改进算法对电力变压器局部放电进行定位。文献[6]以局部放电产生的电磁辐射波为基础，利用超宽带射频定位技术完成了局部放电源的定位试验。文献[7]通过对超声信号进行频谱分析来对超声波的等值声速进行修正进而确定出局部放电源的位置。此外，电脉冲法、超高频法等方法也常用于解决变压器局部放电定位问题[8-10]。

由于超声波定位法原理简单、抗干扰能力强，因此逐渐成为变压器局部放电定位的主要方法。人们也通过将超声波法与各类定位算法相结合提出了许多基于智能算法的超声波定位方法。粒子群优化(Particle Swarm Optimization, PSO)算法是群体智能算法的一种[11-12]。该算法物理概念明确，收敛性好。但存在易陷入局部最优、参数依赖性大等不足，针对这些问题国内外研究学者提出了许多改进方法[13-15]。基于自然选择的粒子群算法可以提高标准PSO的求解精度和收敛速度[16]。将其用于求解变压器超声定位问题，并与标准PSO得到的结果进行对比，结果表明改进后的PSO算法在定位精度和搜索范围上都有所提高。

1 NS-APSO算法的提出

1.1 标准PSO算法

PSO算法最早提出于1995年，是一种基于随机初始解的搜索算法[17]。算法以“群体”和“进化”为基本概念，将每个解看作搜索空间中的一个粒子。每个粒子都有一定的速度，其大小根据自身历史经验和种群经验进行动态调整。粒子通过不断地迭代飞行来寻找空间中最优解的位置，每次迭代，粒子的速度和位置按照下式进行更新。

(1)

(2)

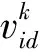
1.2 PSO算法的改进

标准PSO算法容易陷入局部最优问题主要是由于其惯性权重ω被固定，不能根据算法实际收敛情况进行调整而导致的。因此，让惯性权重能够根据种群收敛情况进行动态调节是对算法进行改进的主要思路。自适应参数调节的思想就是首先通过对粒子群早熟收敛程度进行评判，在进一步对惯性权重进行调节[18]。评判粒子群早熟收敛程度的标准如下：

设种群中粒子的总数为N，迭代k次后第i个粒子的适应度为fi，种群的平均适应度为favg，当前最优粒子的适应度为fm，并定义收敛度Δi来对种群早熟收敛程度进行评判，其计算式如下：

Δi=|fm-favg|

(3)

Δi的大小反映了种群早熟收敛的程度，Δi越小则说明种群早熟收敛程度越高。惯性权重的更新策略由每个粒子的适应值与种群平均适应值的关系来确定，具体如下：

若fi优于favg则表示粒子已经相对接近最优解，为了保证收敛的稳定性，不需要很大程度上继承上一代的速度，因此将它们的惯性权重取为ωmin。

若fi次于favg则表示粒子距离全局最优点的距离还相对较远，为了加速他们向最优处靠拢，根据其早熟程度对惯性权重赋予不同的值，其具体大小为：

(4)

通过在标准粒子群算法中引入参数自适应调整的方法提高了算法全局搜索能力，保证了算法不会陷入局部最优的问题，但降低了算法的收敛精度。为了解决这一问题，通过引入自然选择的思想来提高算法的收敛精度。其具体方法为：种群每更新一次，都计算出种群中每个粒子的适应度值，并根据粒子适应度的大小关系将种群均分为两部分。适应度差的那部分粒子的速度和位置将被适应度好的那部分粒子的速度和位置替代。通过粒子的更新替换使得种群整体的质量得到了提升，提高了算法的收敛精度。

1.3 NS-APSO算法流程

NS-APSO算法的基本原理是：在APSO的基础上引入自然选择的思想，在保证粒子良好的搜索能力的前提下，通过粒子的更新替换提高种群粒子收敛的精度。

该算法的基本流程如下：

(1)初始化种群，在搜索空间的各个位置生成具有一定初始速度的粒子；

(2)按照速度、位置更新方程对粒子的速度和位置进行更新，同时根据适应度函数求出每个粒子的适应值fi，若fi优于粒子个体极值pi则令pi=fi；同理若fi优于种群最优极值pg，则令pg=fi；

(3)判断算法的终止条件是否满足，若满足转向(6)，否则转向(4)；

(4)将种群中的粒子按照适应度优劣进行排序并均分为两部分，适应度差的那部分粒子的速度和位置将被适应度好的那部分粒子的速度和位置代替；

(5)根据早熟收敛程度对惯性权重ω进行调整并转向(2)；

(6)输出pg的值，算法结束。

2 基于超声波的变压器局部放电定位

2.1 局部放电超声波定位的数学模型

超声定位的主要原理是将超声波传感器测得超声波信号用相应装置转化为时延信号后带入超声定位的数学模型中去求解局部放电点的位置。将变压器用一个立方体等效，并以该立方体的一个顶点为原点建立空间直角坐标系(见图1)。P表示局部放电点， S1～S3分别表示传感器1～3， S0为传感器1～3的参考传感器。其中放电源P的位置为(xs,ys,zs)，传感器S1～S3的位置为(xi,yi,zi)(i=1、2、3)，参考传感器S0的位置为(x0,y0,z0)。

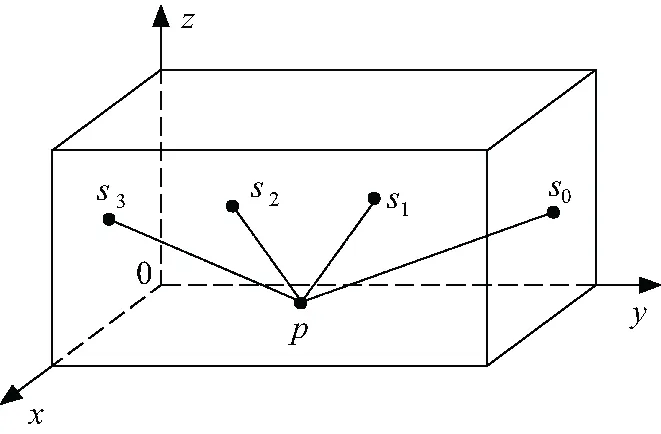
图1 变压器局部放电定位模型

根据图1中的几何信息可知：传感器S1、S2、S3与参考传感器S0到放电源P点的相对距离差Δli为：

(5)

式中i=1,2,3。记超声波到达传感器S1、S2、S3的时间与到达参考传感器S0的时间差为τi(i=1、2、3)，超声波在油中传播的速度为v；则显然有：

Δli≈τiv

(6)

根据式(6)可知局部放电源的实际位置会使得式(7)的函数值很小。

(zi-zs)2]1/2-[(x0-xs)2+(y0-ys)2+

(z0-zs)2]1/2-τiv)]}

(7)

式(7)为一个非线性方程，直接进行求解十分困难，为了简化计算将其等效为带约束的优化问题：

(8)

式中xl,yw,zh分别为变压器的长、宽、高的值；v表示超声波在变压器中的传播速度。

2.2 变压器内超声波传播过程分析

变压器内部结构复杂，除了线圈、油道、绝缘油纸等固体介质外，油箱内还充满变压器油。同时，在超声波传播过程中还伴有折射、吸收、色散等现象发生，也会造成超声波信号出现变化。因此，如果按照变压器实际结构来分析超声波在变压器中的传播几乎是不可能的。为了便于分析，在研究变压器内部超声波传播过程时，将变压器内部等效为层状介质结构，并以分析几何声学的方法来对变压器内超声波传播过程进行分析[19]。

研究发现，若超声波到达油箱壁后继续沿着油箱壁至传感器会出现很大程度的衰减，而如果直接穿过油层和油箱壁到达传感器衰减就会小很多，因此传感器接收的超声波信号也主要是这部分信号，即沿着图2中的路径1传播的超声波信号(见图2)。

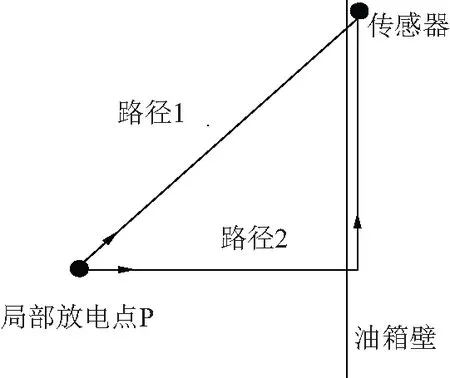
图2 变压器内超声波传播途径

3 基于NS-APSO算法的算例分析

按照图1所给的局部放电定位模型设置一个规格为1000 mm×1200 mm×800 mm的油箱，油箱周围四个面上分别各安装一个传感器，各自的位置分别为：S0(800,820,0)mm、S1(1000,420,346)mm、S2(345,782,800)mm、S3(0,468,386)mm。

粒子群算法参数设置：设种群规模为N=100；最大迭代次数M=100；学习因子c1=c2=2；最大速度vmax=20，标准粒子群算法中惯性权重固定为ω=0.729，NS-APSO算法中最大惯性权重ωmax=0.9，最小惯性权重ωmin=0.3。

算例中，以最优粒子与局部放电点的距离大小作为适应度函数。种群最优粒子与局部放电点的距离越近表示适应度越好，算法迭代完成后输出全局最优值表示求得的局部放电点位置。

为了验证算法的有效性，取三次不同的点作为局部放电源的位置，每次分别用标准PSO算法和NS-APSO算法来进行定位。

第一次试验中取局部放电源P的位置取为(221,436, 576) mm，各传感器相对时延分别为τ1=-0.063ms，τ2=-0.332 ms，τ3=-0.429 ms。

第二次试验中取局部放电源P的位置取为(452,618, 576) mm，各传感器相对时延分别为τ1=-0.054ms，τ2=-0.285 ms，τ3=-0.134 ms。

第三次试验中取局部放电源P的位置取为(768,324, 436)mm，各传感器相对时延分别为τ1=-0.278 ms，τ2=0.043 ms，τ3=0.086 ms。

三次定位所得结果如表1所示。

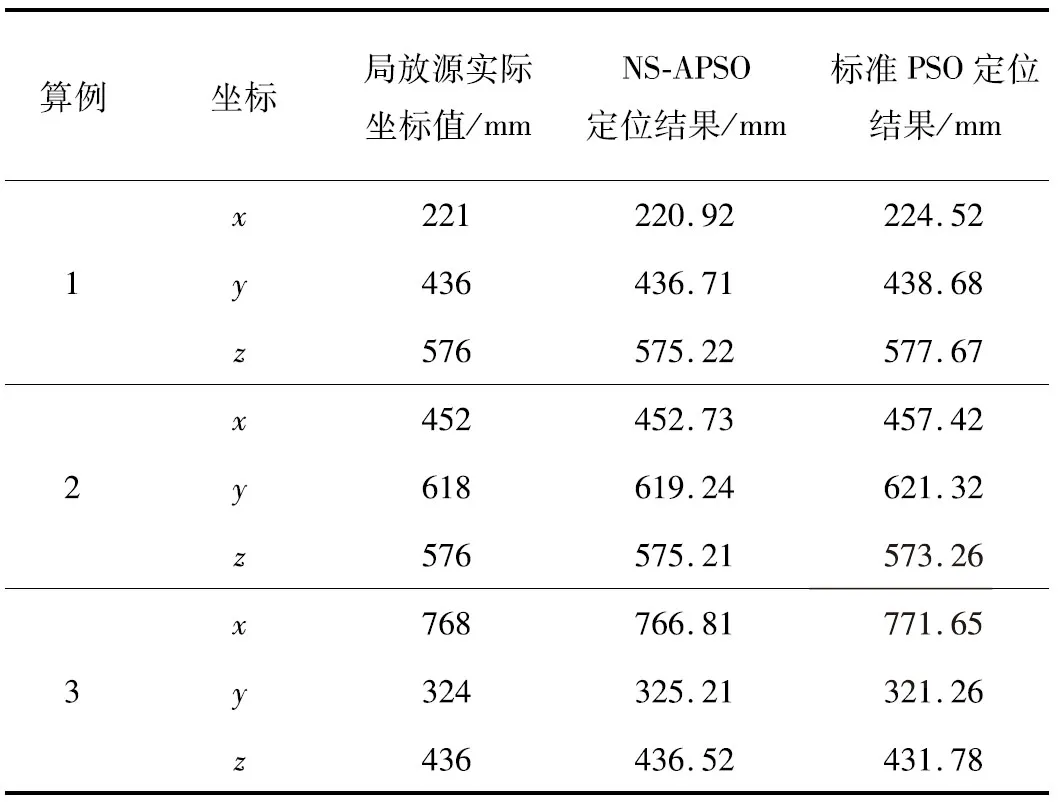
表1 标准PSO与NS-APSO定位结果比较

为了验证NS-APSO算法相对于标准PSO算法是否具有更高的定位精度，对所得结果进行了误差对比分析，定位误差：

式中(xs,ys,zs)为局部放电点的实际位置;(xi,yi,zi)为算法求得的位置;结合表1的数据得到标准PSO和NS-APSO的误差数据如表2所示。

由表2所得结果可以看到：NS-APSO算法大大降低了定位误差，提高了算法的收敛精度。

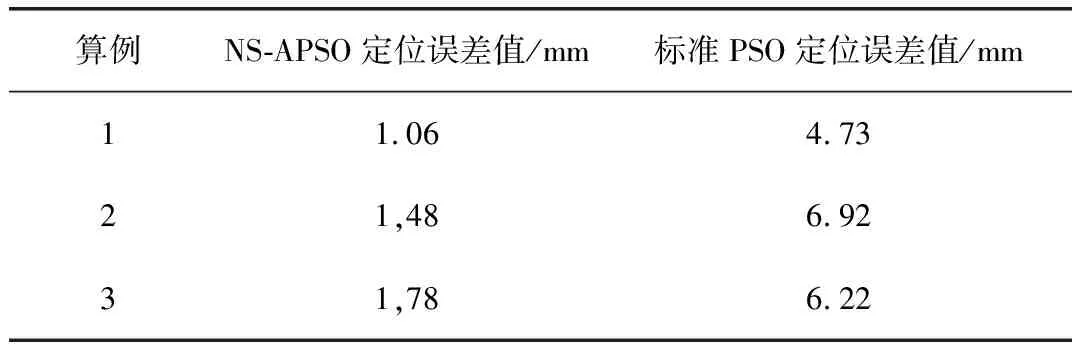
表2 标准PSO与NS-APSO定位结果误差分析

为了验证NS-APSO算法是否具有扩大搜索范围、避免种群陷入局部最优的作用，以算例1为例，在Matlab中绘制出两种算法适应度随迭代次数的变化关系曲线(见图3、图4)

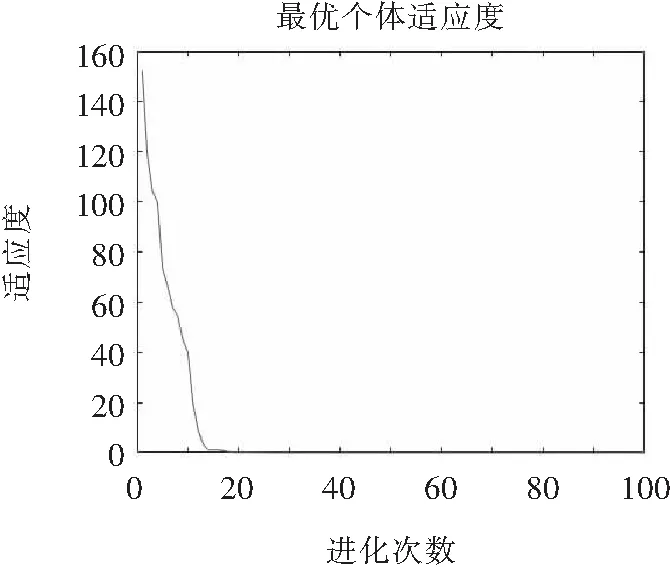
图3 标准PSO适应度值与迭代次数关系曲线

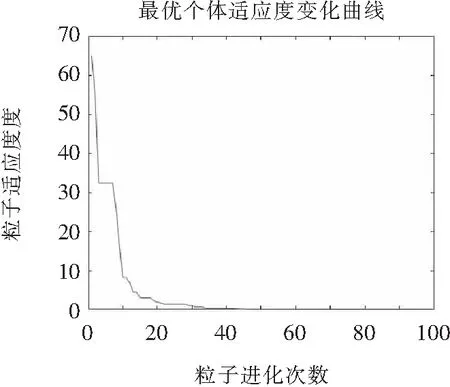
图4 NS-APSO适应度值与迭代次数关系曲线

对比图3和图4可知：相对于标准PSO算法，NS-APSO算法扩大了种群中粒子的搜索范围，降低了种群出现早熟收敛与粒子陷入局部最优的概率。

4 基于Matlab GUI的软件设计

4.1 Matlab GUI简介

图形用户界面(Graphical User Interface, GUI)是由窗口、按钮等图形对象构成的用户界面[20]。简单的界面、实时的人机交互、以及基于Matlab的强大的矩阵、数值处理能力，使得利用GUI设计的软件具有很大的可操作性和普适性。尤其在现场试验中，GUI仿真代码的不可见性为一些不熟悉Matlab编程的人群提供了操作界面的可能。

4.2 基于Matlab GUI的变压器局部放电超声定位软件设计

考虑到工程实际中变压器的尺寸各不相同，设计了图5所示的用户界面。该界面分为三部分，分别为：数据输入输出区、图形输出区、控制面板区。

数据输入输出区用于输入变压器的尺寸、各传感器的位置、相对时延等数据，同时输出放电点的位置；图形输出区通过图形的形式动态地给出了变压器局部放电源定位的过程；控制面板区用于实现数据清除、计算以及程序退出的功能。

图5 变压器局部放电超声定位软件界面

为了验证软件的实用性，以算例1为例，对局部放电源P进行定位。将变压器尺寸、各传感器位置、相对时延输入到界面中并进行计算得到结果如图6所示。

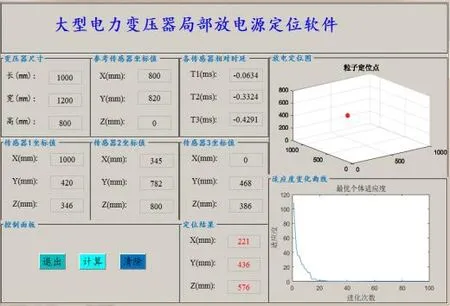
图6 软件定位结果

软件运行结果显示：该软件达到了很好的预期效果，定位结果精确。放电源实际位置的图形可视化也为检修人员快速找出局部放电点的位置提供了帮助。

5 结束语

文中提出了一种基于自然选择的自适应粒子群算法，该算法以自适应粒子群算法为基础融入了自然选择的思想。对比标准PSO和NS-APSO求解局部放电数学模型的结果发现：NS-APSO算法具有更高的收敛精度和全局搜索能力，克服了标准PSO算法存在的易早熟收敛的问题。

基于Matlab中的GUI模块设计了一款能够对不同尺寸的变压器进行局部放电超声定位的软件，该软件运行结果理想，操作简单具有很强的实用性。