基于压缩感知的智能电能表信号压缩

张璨辉，赵丹，解玉满，肖建红，刘翔斌

(国家电网湖南省电力公司，长沙 410004)

0 引 言

智能电网是一种集成了多种先进计算技术与通信技术，使得能源管理与分配更为精准高效的电网系统[1]。其中，以智能电能表为代表的各类高级计量设备(Advanced Metering Infrastructure，AMI)可以实现电网中从发电到用户的各节点的精确测量与双向通信，是智能电网体系中最为重要的一类基础设施[2-3]。然而，由于使用场景的特殊性，智能电能能表在硬件配置，如电池电量与通信带宽方面受到许多限制，因此无法直接传输大规模数据。例如，由于不满足能耗与带宽要求，智能电能表难以支持功率分解(Power Disaggregation)任务中所需的实时功率信号传输，这类信号的采样频率通常约为1k Hz[4]。

另一方面，在设备级别上的精确信号对于智能电网的高效运行是非常重要的。例如，在需求响应与功率分解等过程中，需要大量AMI设备上的负载特性。在采样率较低，智能电网中可以较好地支持将总负载信号分解到单个设备层次，这一技术通常用于非侵入式负载监控(Non-Intrusive Load Monitoring，NILM)等任务[5-6]。但是，仅仅以较低采样率对聚合后的功率信号进行采样，采样信号中的信息并不足以完成功率分解这样更为复杂的任务，因此无法精确地获得单个设备上的功率信号[7-8]。

因此，对于这些问题，信号压缩成为一项必要的技术。已有文献中已经对智能电网中的信号压缩进行了较多研究，典型的有：

(1)基于小波变换(Wavelet Transform)的信号压缩[9]。利用小波变换的多分辨率分析(Multi-Resolution Analysis，MRA)，可以同时实现功率信号的压缩与降噪；

(2)基于奇异值分解(Singular Value Decomposition，SVD)的信号压缩[10-11]。这类方法对原始信号的重建效果通常优于小波变换，但复杂度很高，并不适用于智能电能表这类小型终端；

(3)基于张量分解(Tensor Decomposition)的信号压缩[12]。将信号组合成高阶张量处理，在混合型信号的压缩效果上优于奇异值分解方法。类似地，张量分解法也具有高复杂度；

文中提出基于压缩感知(Compressed Sensing)的智能电能表信号压缩技术，并通过实验说明，该方法在保持信号重建效果的同时，效率优于传统方法，有助于实现精确高效的功率分解。

1 功率信号的建模

智能电能表在用户端的典型应用模式为：电表采集用户所使用设备(如家用电器)的总功率信号，通过一个数据集中器(Data Concentrator Unit，DCU)发送到中心服务器。而家用电器因设备的工作原理不同，其负载和功耗特性也存在较大差异。另外，根据设备的使用目的，工作的时间也不同。因此，从原理上直接对智能电能表所获得的功率信号建模是困难的，文中采用了经验模型的方式[13-14]。

四种模型可用于家用电器功率信号的经验建模，分别是开-关模型(On-Off)、开-关衰减模型(On-Off Decay)、稳定最小-最大模型(Stable Min-Max)与随机模型(Random Model)。通过分析数据特征可以确定模型中的参数与概率分布。

首先讨论最基本的只与电阻性负载有关的开-关模型。这一模型仅考虑两种状态：当电器工作时为开状态，具有固定的功率，记为pactive；当电器不工作时为关状态，具有零功率或极低的功率，记为poff。因此，第i个电器在t时刻的功率可以表示为：

(1)

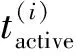
开-关衰减模型是开-关模型的变体。与最简单的开-关模型不同的是，开-关衰减模型中考虑了感性负载的行为。在这一模型中，当具有感性负载的电器开启时，首先会发生电流的快速增大，然后再随时间平稳衰减，在关闭时也有类似的过程。当存在包含交流电动机等组件的电器如，引入这一模型就成为必要的。开-关衰减模型中，第i个电器在t时刻的功率可以表示为：

p(i)(t)=

(2)

当电器中存在非线性负载，这类电器随机地处于最小或最大功率状态[16-17]。稳定最小-最大模型考虑了这类负载的特性。由于随机性，对非线性负载功率的预测是困难的，但依然可以认为负载在εi周期内具有固定的功率。在稳定最小-最大模型中，第i个电器在t时刻的功率可以表示为：

(3)

稳定状态功率为：

(4)

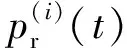
最后一种经验模型为随机模型，针对功率变化较大的计算机等设备。其功率可以简单地表示为：

(5)

因此，对于一个记录了多个电器设备总功耗的智能电能表，将其所记录的功率记为pSM(t)，则pSM(t)可以表示为所有设备的功率之和，即：

(6)

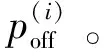
2 基于压缩感知的功率信号压缩

由智能电能表直接采样的功率信号必须经过压缩才可用于后续的功率分解等任务，文中针对这一问题提出基于压缩感知的功率信号压缩技术。为了将压缩感知用于功率信号，功率信号必须成为稀疏的[18-20]。通过上文所述的经验模型，可以用稀疏的表示矩阵描述家用电器的功率信号。将其进一步扩展，得到智能电能表功率信号的稀疏表示。为方便起见，下文的公式中将省略时间变量t。智能电能表所采集的功率信号可以表示为矩阵形式：

p=Ψs

(7)

其中Ψ为N×N的信号表示矩阵，s是一个N×1的向量，包含Q(Q远小于N)个较大的元素与N-Q个接近0的元素。为便于计算，可以将接近0的N-Q全部视为0，此时的s向量用s(Q)代替。Q值的选择将影响压缩信号的重建效果，体现了稀疏度与精确性的权衡。在本文中，Q值通过能量占比来确定：若给定的目标能量占比为k，s(q)向量非零元素个数为q，则Q值为保留原信号能量的k倍时，所要求的最小q值，即：

(8)

y=ΦΨs

(9)

其中Φ为投影矩阵，由M个投影向量组成。在压缩感知问题中，投影矩阵的设计对于压缩信号的重建效果十分关键。相干性(Coherence)是评估投影矩阵的常用指标。当投影矩阵与表示矩阵之间的相干性越小，对于原始信号的重建效果越好。通常选择使用冲激函数(Spike Function)或高斯分布函数得到投影矩阵Φ，使用离散余弦变换(Discrete Cosine Transform，DCT)或小波变换等方法得到表示矩阵Ψ。

(10)

3 实验结果与分析

在实验中，使用了智能插头收集单个家用电器的功耗数据。为了进行全面的分析，对于功率信号的四种经验模型都选择了对应的电器，分别包括：

(1)开-关模型：电灯，咖啡机，烤面包机；

(2)开-关衰减模型：冰箱，冰柜，烤箱；

(3)稳定最小-最大模型：干衣机；

(4)随机模型：台式电脑。

根据电器历史数据，得到相应的经验模型参数如表1所示。

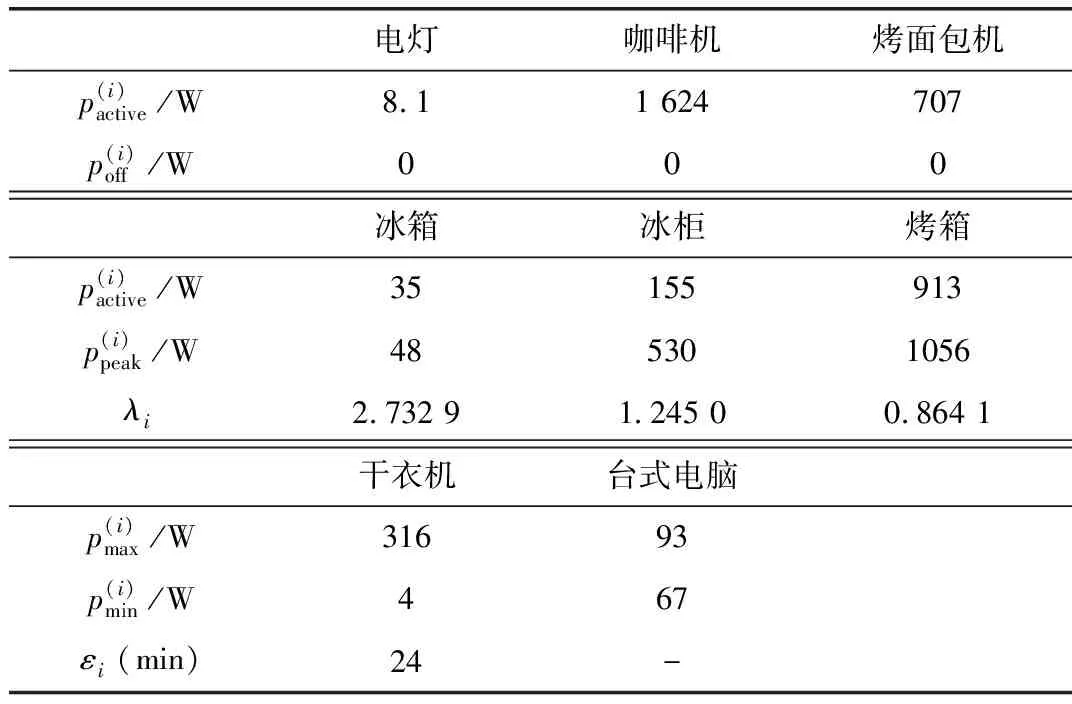
表1 部分经验模型参数的估计值

图1给出了经验模型与实际测量值的对比，图中的横轴为时间，单位为min。如前文所述，开-关模型中的电器具有固定的功率，模型值与实际值之间的微小差异可视为测量误差。开-关衰减模型中，误差不仅包括测量误差，还包括使用最小二乘法估计衰减系数时的精度误差，但误差相对于实际功率也是可忽略的。而对于稳定最小-最大模型与随机模型，由于随机性的存在，从图1中可以看出，模型误差相对较突出。但另一方面，在统计特征上看，经验模型与实际测量值依然是一致的。图1中的结果说明了文中使用的功率信号经验模型的有效性。

图2给出了能量占比k与稀疏度的关系曲线。这里的定义为ρ=(N-Q)/N，N取为256。图中评估了三种生成表示矩阵的方式：Haar小波变换(HWT)、离散余弦变换(DCT)与差分变换(Difference Transform，DT)。图中结果说明，HWT方法在生成稀疏表示矩阵上效果最优

图3对基于压缩感知的信号压缩与基于小波的方法在信号重建效果上进行了比较。为更为全面地进行评估，实验中选择了多种生成表示矩阵与生成投影矩阵的方法组合。图3中的横轴为压缩率，定义为信号压缩后所省略的存储空间(比特数)比率。结果表明，基于压缩感知的方法相比小波变换具有显著优势，且最优组合为使用HWT生成表示矩阵与使用高斯分布函数生成投影矩阵。

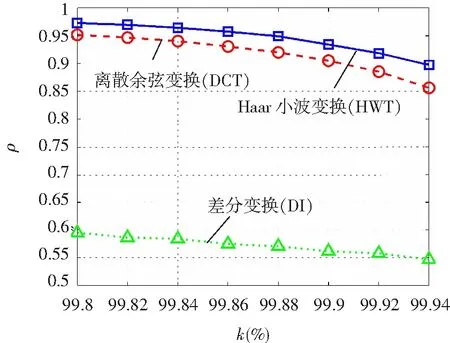
图2 稀疏度与能量占比的关系曲线

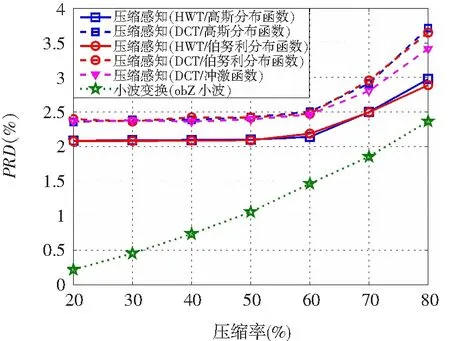
图3 压缩感知与小波变换的信号压缩效果比较

4 结束语

文章针对智能电能表的应用场景设计了基于压缩感知的信号压缩方案，以支持AMI设备中低能耗、窄带宽条件下功率分解等任务所要求的功率信号的精确传输。首先使用四种经验模型对智能电能表信号进行建模，并验证了经验模型的有效性。基于经验模型，对压缩感知方法的信号压缩效果进行了验证，得到了最优的投影矩阵与表示矩阵生成方案，说明了文中方法相比小波变换方法的优势。