高速连续强冲击下的滚子链动力学特性研究

王 凯， 李 勇， 田 楠， 申亚琳， 刘宗超

(1.西北机电工程研究所,陕西 咸阳 712099； 2.内蒙古北方重工集团有限公司，内蒙古 包头 014030)

滚子链传动通过链条与链轮轮齿之间的啮合来传递运动和动力，是一种带有中间挠性件的非共轭啮合传动，具有结构紧凑、工作可靠、承载能力大、传动效率较高、平均传动比准确等优点[1-4]。目前，滚子链的相关研究已取得丰富成果。理论研究方面：程明等[5-6]通过理论分析和试验验证，验证了滚子链传动的多边形效应与动载荷；杨仁民等[7]通过建立数学运动方程来表述多边形效应对链传动的实时影响；许立新等[8]建立了套筒、滚子链传动系统有限元模型，较精确地揭示了链传动的冲击特性；樊鹏等[9]研究了链传动中齿轮与链节啮合冲击载荷变化规律；闫思江等[10]结合链传动特性，对引起链传动动载荷的主要原因进行了仿真分析；郝驰宇等[11]建立了链轮磨损和链条磨损的故障仿真模型，为滚子链传动的故障机理分析及故障诊断提供一定依据。随着常规链传动运行机理研究的逐渐深入，新型滚子链传动研究与复杂工程应用研究已成为主要研究方向。王丽萍等[12]针对常规链传动中振动、磨损等问题，设计出一种新型滚子链传动，比常规滚子链的啮合冲击力更小，传动更平稳；刘雨等[13]对输送滚子链进行建模与仿真，探究了滚子链爬行的主要原因；倪健健等[14]以某送料机的链传动机构为对象，分析了振动与载荷情况，为整机的优化提供借鉴；王欢等[15]以低速柴油机正时链传动机构为对象，研究了其运动学和动力学特性，为减小振动和噪声提供依据；徐伟通等[16]以扶梯驱动链系统为对象，研究了其链系统动力学特性和磨损对系统的影响。

链式自动炮是一种通过链条周向转动驱动炮闩往复运动来完成解锁、开闩、抽壳、供弹、输弹、关闩、闭锁、击发等动作的外能源自动炮[17]。输弹机构是链式自动炮的重要组成部分，其主要功能是通过滚子链传动将炮弹快速可靠地输送到炮膛内，并完成闭锁、解锁、抽壳等动作。输弹机构因具有工作冲击载荷(抽壳力等)大、高速连续运转、空间环境狭小密闭等特点，成为链式自动炮故障率较高的子系统[18]。目前，鲜有类似恶劣、独特工况背景的滚子链传动相关研究。

因此，本文通过建立滚子链动力学数学模型，分析影响链式自动炮链传动特性因素，基于UG三维软件和RecurDyn多体动力学分析软件进行链式自动炮滚子链动力学数值模拟，研究了不同影响因素(预紧力、链节间隙、抽壳力)对链传动过程中啮合碰撞力和链速波动影响，为链式自动炮滚子链传动的优化设计提供依据。

1 链式自动炮输弹机构

1.1 结构原理

链式自动炮输弹机构由1个主动链轮、3个从动链轮、链条、导轨、滑块、链围架、闩座、闩体组成，如图1所示。其工作原理如下：主动链轮驱动从动链轮，使链条呈矩形回转运动；滑块固定于主链节上，随链条做矩形回转运动；闩座滑槽抵消滑块的横向直线运动，将链围的矩形回转运动转化为闩座的直线往复运动；闩座的直线往复运动带动闩体将炮弹快速可靠地输进和输出炮膛。

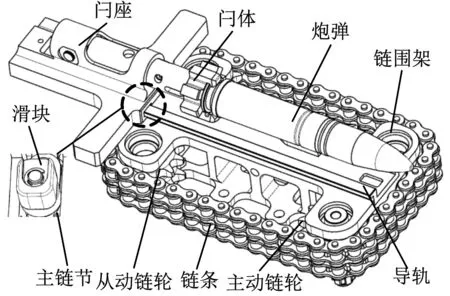
图1 链式自动炮输弹机构示意简图

1.2 运行原理分析

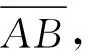
图2 链条运动示意简图

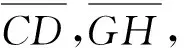
2 滚子链动力学数学模型与分析

2.1 滚子链动力学数学建模

滚子链系统属于多自由度非线性复杂机械系统。为方便建模求解，做出以下假设：① 主、从动轮质量分布均匀，无偏心;② 各链节等速，且各链节的等效质量集中于链节销轴中心;③ 忽略链条横向振动，只考虑纵向动力学模型。

链轮以速度v带动链条沿理论轨迹运动，各滚子链销轴之间的连接等效为弹簧阻尼系统。当滚子输送链运行时，各运动链节以相同的速度v运动，取其中一对相邻链节作动力学分析，如图3所示。其中，相邻链节为主动件，主链节为从动件。

图3 滚子链动力学模型

当相邻链节开始驱动时，t=0时刻，主链节处于自由状态。经过时间t后，主动相邻链节位移为x。则从动件主链节的运动方程为

(1)

式中：m为滚子链节质量；k为弹性系数；c为黏性阻尼系数；v为链轮驱动速度，即链速；Fd为滚子链系统运行产生的动载荷；Fl为滚子主链节所受负载；Ff为滚子链接所受摩擦力。

式(1)的通解为

(2)

式中，F=Fd-Fl-Ff。

(3)

对式(3)求导，可得主链节的速度方程。

(4)

主链节的固有频率

(5)

主链节的系统阻尼比

(6)

根据式(5)和式(6)化简式(4)，可得主链节的速度

(7)

其中，vS为系统结构特性引起的速度波动

(8)

vF为外力与系统结构特性耦合引起的速度波动

(9)

2.2 滚子链动力学分析

从式(7)可以看出，主链节速度除了常量v，还有速度波动量vS,vF。vS仅由系统结构特性决定；vF除与系统结构特性有关，还与外力F有关。因此，为提高滚子链运行平稳性，应尽量减小vF，即减小外力F。外力F由动载荷Fd、摩擦力Ff、负载Fl共同决定。

动载荷Fd主要成因：链条与从动轮角速度周期性的变化，产生附加的载荷；链节进入链轮的瞬间，两者以一定速度相啮合，产生冲击载荷；链条横向振动，也可增大链条传动载荷；链条张紧不好，也会在启动、制动变化时产生惯性冲击载荷。上述成因大多由链传动本身特性决定，链式自动炮链传动结构与运行状态相对固定。因此，动载荷Fd影响参数可简化为链条预紧力FP和链节间隙δ。

摩擦力Ff主要来源于主、从动轮与链节、滑块与闩座的滚动和滑动摩擦，反映了滚子链润滑情况。链式自动炮滚子链在实际工况下利用炮用润滑脂进行润滑，摩擦力已降到相应较低水平。因此，摩擦力Ff对滚子链传动的影响规律研究意义不大。

负载Fl主要来源于链式自动炮击发完毕后的抽壳阻力，其形成原因如下：火药在膛内爆炸形成瞬时高温和高压，使弹丸沿身管向射击方向运动，同时药筒径向膨胀并产生塑性变形，紧贴身管内壁[19-20]，从而产生极大抽壳阻力。抽壳过程是一个包含弹塑性变形、接触、摩擦等复杂因素的瞬态动力学过程，很难建立准确的力学模型，一般简化为1～5 ms的矩形脉冲载荷。因此，负载Fl影响参数可简化为抽壳力峰值FC。

3 滚子链数值模拟分析

本章基于RecurDyn多体动力学分析软件建立链式自动炮滚子链动力学仿真模型，以滚子链动力学数学模型分析得到的滚子链传动特性影响因素(预紧力FP、链节间隙δ、抽壳力FC)为参数，以滚子链链传动过程中主动链轮啮合碰撞力和主链节链速标准差为指标，研究链式自动炮滚子链动力学特性，为链式自动炮滚子链传动的平稳性设计提供理论依据。其中，主动链轮啮合碰撞力最大值和平均值反映了滚子链传动过程中振动特性的峰值和均值；主链节链速标准差反映了滚子链运行的平稳性，均对链式自动炮供输弹机构的传动特性影响重大。

3.1 建立链式自动炮滚子链模型

利用三维建模软件UG绘制某链式自动炮输弹机构零部件模型；将UG零部件模型导入到多体动力学仿真软件RecurDyn中装配，并设置相应材料属性:弹性模量2.06×1011Pa、剪切模量7.78×1010Pa、密度7.85×103kg/m3；滚子链链条和链轮通过RecurDyn软件中的chain模块建立，并与已导入的UG模型建立相应的约束和接触；设置主动链轮驱动角速度80π rad/s，对应链式自动炮高射频工况(600发/min)，理论链速为7 708 mm/s；抽壳力加载在闩体镜面上，为一段5 ms矩形脉冲载荷。

主、从动链轮与滚子链的接触计算是一个不断检测的过程，根据穿透深度及变化来计算接触力。当计算过程中主、从动链轮与滚子链节的实际穿透深度小于最大穿透深度时，计算接触力；一旦检测到实际穿透深度大于最大穿透深度，则接触失效，不再计算接触力[21]。接触理论采用非线性弹簧阻尼模型，其法向接触力计算公式

(10)

(11)

(12)

式中：k为接触刚度系数；c为黏性阻尼系数；δ为接触穿透深度；m1为刚度指数；m2为阻尼指数；m3为凹痕指数；μ1,μ2为接触物体材料的泊松比；E1,E2为接触物体材料的弹性模量。

图4 链式自动炮滚子链动力学仿真模型

3.2 不同因素动力学特性分析

3.2.1 预紧力FP影响规律

为研究预紧力FP对于链式自动炮滚子链动力学特性的影响，结合实际工况与仿真情况，固定链节间隙0.2 mm、抽壳力10 000 N，预紧力FP分别取1 000 N,2 000 N,3 000 N,4 000 N,5 000 N,6 000 N进行仿真分析。从图5得出，在刚启动的0～0.015 s时，主动链轮所受碰撞力和链速均呈现较大震荡，然后趋于稳定震荡，属于正常的启动冲击；在0.030～0.035 s时，滚子链滑块运行到抽壳位置，主动链轮所受碰撞力和链速再次出现较大震荡，然后趋于稳定震荡；在0.081～0.083 s时，主链节啮入从动链轮(与主动链轮处于对角位置)，主动链轮所受碰撞力和链速再次出现较大震荡。抛除0～0.015 s时的启动冲击曲线段，提取出不同预紧力条件下的指标响应特征值如表1所示，并绘制出图6曲线，可知：链速标准差随着预紧力的增大呈现出先急剧减小、后基本趋于稳定，表明当预紧力FP大于4 000 N后，滚子链链速波动不再大幅增大；主动链轮碰撞力平均值随预紧力的增大呈近似线性增大趋势，递增率823.2 N/1 000 N；主动链轮碰撞力最大值随预紧力的增大呈近似线性减小趋势，递减率2 201.2 N/1 000 N。

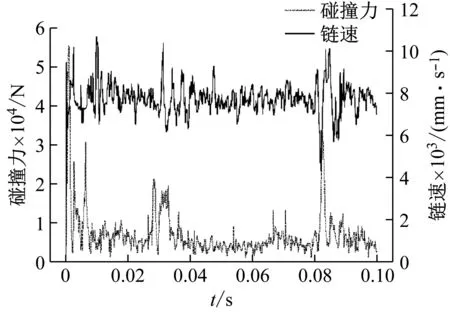
图5 预紧力FP=1 000 N时，碰撞力、链速与时间关系曲线

表1 不同预紧力的响应特征值

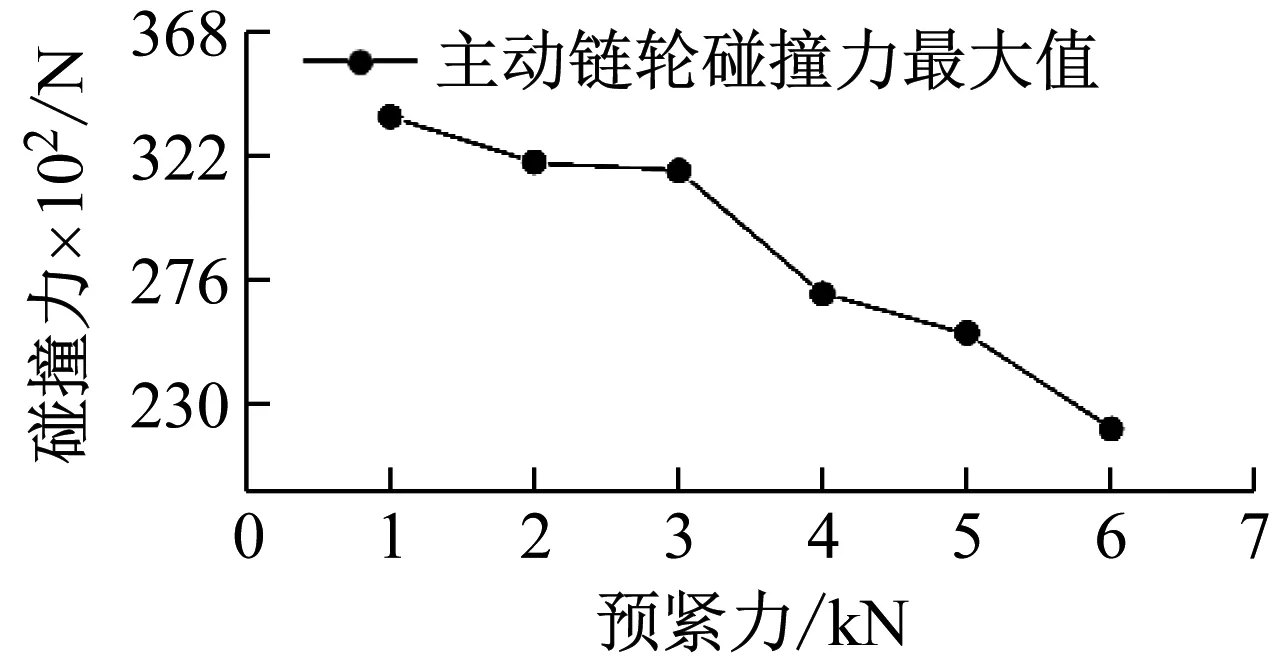
(a)

3.2.2 链节间隙δ影响规律

为研究链节间隙δ对于链式自动炮滚子链动力学特性的影响，结合实际工况与仿真情况，固定预紧力4 000 N、抽壳力10 000 N，链节间隙δ分别取0.05 mm,0.10 mm,0.15 mm,0.20 mm,0.25 mm,0.30 mm进行仿真分析。从图7得出，在刚启动的0～0.015 s时，主动链轮所受碰撞力和链速也呈现出较大震荡，然后趋于稳定震荡，同样属于正常的启动冲击；在0.030～0.035 s时，滚子链滑块运行到抽壳位置，主动链轮所受碰撞力和链速再次出现较大震荡，然后整体一直趋于稳定震荡中。抛除0～0.015 s时的启动冲击曲线段，提取出不同链节间隙条件下的指标响应特征值如表2所示，并绘制出图8曲线，可知：链速标准差在链节间隙0.05～0.15 mm内急剧增大，最大递增量137.5 mm·s-1/0.05 mm；在链节间隙0.15～0.20 mm内基本稳定；在链节间隙0.2～0.3 mm区间缓慢减小，递减率18.5 mm·s-1/0.05 mm。该结果表明链节间隙增大到0.15 mm的过程中，链速波动最为明显；随着链节间隙的继续增大，链速波动略有减小。主动链轮碰撞力平均值随链节间隙的增大呈近似线性增大趋势，递增率1 563.2 N/0.05 mm。主动轮碰撞力最大值随着链节间隙的增大整体呈现先略有减小、后急剧增大、再减小趋势，最大递增率13 005 N/0.05 mm。

图7 当链节间隙δ=0.20 mm时，碰撞力、链速与时间关系曲线

表2 不同链节间隙的响应特征值

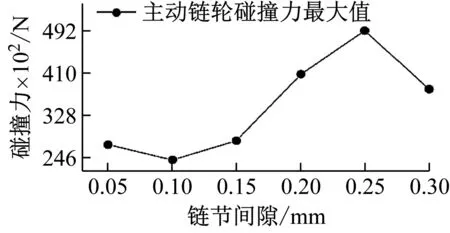
图8 链节间隙与响应特征值关系曲线

3.2.3 抽壳力FC影响规律

为研究抽壳力FC对于链式自动炮滚子链动力学特性的影响，结合实际工况与仿真情况，固定预紧力4 000 N、链节间隙0.2 mm，抽壳力FC分别取5 000 N,10 000 N,15 000 N,20 000 N,25 000 N,30 000 N进行仿真分析。从图9得出，主动链轮所受碰撞力和链速除在刚启动0～0.015 s区间、抽壳位置0.030～0.035 s区间，均趋于稳定震荡。抛除0～0.015 s时的启动冲击曲线段，提取出不同抽壳力条件下的指标响应特征值如表3所示，并绘制出图10曲线，可知：链速标准差在抽壳力5 000～20 000 N区间近似线性缓慢增大，递增率6.3 mm·s-1/5 000 N；在抽壳力20 000～30 000 N区间急剧增大，最大递增量56.8 mm·s-1/5 kN。该结果表明抽壳力增大到20 000 N的过程中，链速波动缓慢增加；随着抽壳力的继续增大，链速波动急剧增大。主动链轮碰撞力平均值在抽壳力5 000～25 000 N区间近似线性缓慢增大，递增率174.3 N/5 000 N；在抽壳力25 000～30 000 N区间急剧增大，最大递增量604 N/5 000 N。主动链轮碰撞力最大值随着抽壳力的增大呈现线性近似增大趋势，递增率8 145 N/5 000 N。

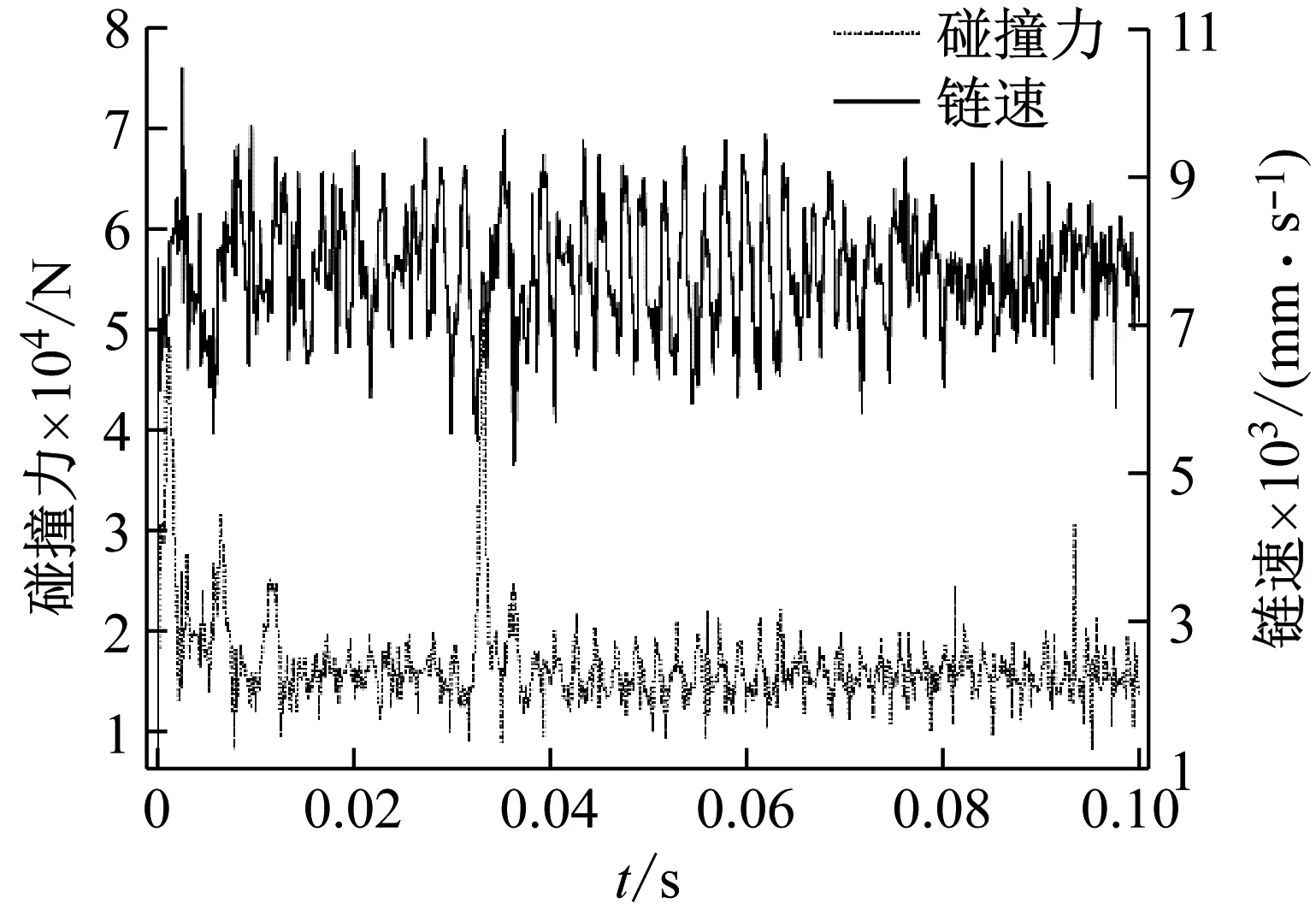
图9 抽壳力FC=10 000 N时，碰撞力、链速与时间关系曲线

表3 不同抽壳力的响应特征值

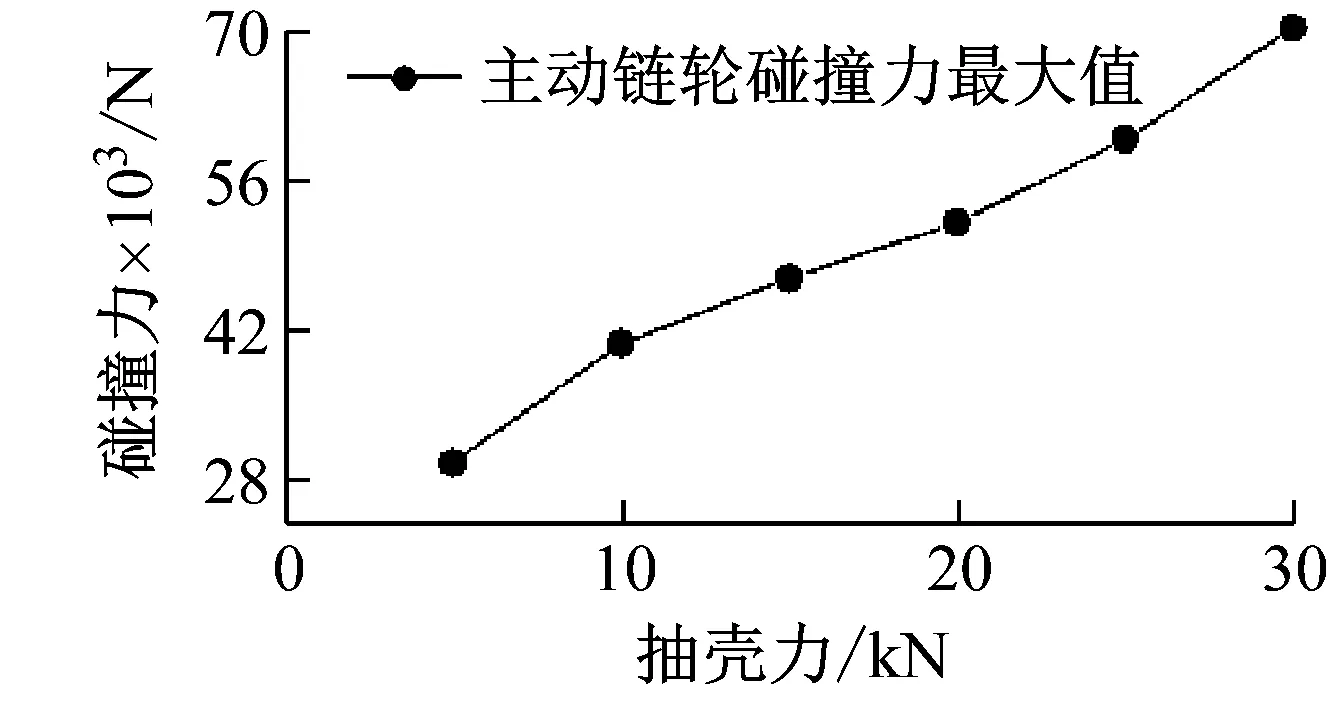
图10 抽壳力与响应特征值关系曲线

4 结 论

本文建立了滚子链动力学数学模型，并以链式自动炮滚子链为例进行仿真分析，获得了预紧力、链节间隙、抽壳力对滚子链动力学特性的影响规律，得出以下结论：

(1) 在其他参数条件固定的情况下，滚子链链速随着预紧力的增大呈现出先急剧减小、后基本趋于稳定，且当预紧力FP≥4 000 N后，滚子链链速波动不再大幅增大；随链节间隙增大到0.15 mm的过程中，链速波动最为明显，后续略有减小；随抽壳力增大到20 000 N的过程中，链速波动缓慢增加，后继急剧增大。

(2) 在其他参数条件固定的情况下，主动链轮碰撞力平均值随预紧力的增大呈近似线性增大趋势，递增率823.2 N/1 000 N；随链节间隙的增大呈近似线性增大趋势，递增率1 563.2 N/0.05 mm；随抽壳力增大到25 000 N的过程中呈近似线性缓慢增大，递增率174.3 N/5 000 N；后续急剧增大，最大递增量604 N/5 000 N。

(3) 在其他参数条件固定的情况下，主动链轮碰撞力最大值随预紧力的增大呈近似线性减小趋势，递减率2 201.2 N/1 000 N；随着链节间隙的增大整体呈现先略有减小、后急剧增大、再减小趋势，最大递增率13 005 N/0.05 mm；随着抽壳力的增大呈现线性近似增大趋势，递增率8 145 N/5 000 N。

(4) 链式自动炮滚子链选取预紧力4 000～6 000 N、链节间隙0.05 mm、抽壳力越小时，主动链轮碰撞力和主链节链速波动相对较小，有利于链式自动炮滚子链的平稳性传动。