跑步荷载模型试验建模与实测对比

陈 隽， 周戈杰， 王鹏程

(1.同济大学 土木工程学院，上海 200092；2.同济大学 土木工程防灾国家重点实验室，上海 200092)

单人、人群完成步行、跳跃、跑步、踏步、原地屈伸、跳舞、瞬时起立或坐下等动作时通过双足对支撑结构施加的动力作用称为人致荷载，由此导致的工程结构振动称为人致结构振动。振动幅度过大时会造成结构上的使用者对振动有感、头晕、心慌等振动舒适度问题，或者影响对振动敏感的高精密设备的正常使用，严重时则可能造成结构局部构件破坏甚至整体破坏、人员伤亡等安全问题[1-6]。

跑步运动是极为常见的一种运动形式，尤其随着近年来的全民健身热，参加5 km、马拉松之类的体育活动的人数迅速增加。据报道，2014年我国马拉松赛事运营的收入就达到20亿元，市场规模超百亿元，2015年又增了近50%，2019年更是达到了1 828场次，如表1所示。此外，一些多层体育场馆室内、高层建筑的内部以及建筑屋顶等也开始设计有跑道，方便建筑使用者就近开展跑步活动，如图1所示。

在跑步运动中，当人的跑步频率与支撑结构的自振频率接近时，支撑结构会产生较大的振动，可能造成振动舒适度问题，严重时甚至可能诱发公共安全事件。尤其伴随着建筑材料轻质化、建筑功能多样化的需求，以及开敞、轻盈建筑美学的普及，建筑楼盖、人行桥等结构设计向着大跨度、轻柔方向发展。此类结构自振频率与人的跑步频率范围重合，容易出现人致结构振动问题。例如：美国旧金山金门大桥曾由于大量人群跑步过桥造成大幅振动，引起桥上行人的不适；成都某理工大学校园内一跨度不大的混凝土人行桥，在学生早操跑步通过时剧烈振动，造成了人群的恐慌[7]。上述例子表明，在大跨度结构设计过程中有必要进行人致结构振动分析。

表1 近年来我国马拉松赛事举办场次与参赛人次

(a)(b)

正确的荷载取值是分析跑步荷载所引起的结构振动的基本前提，然而，我国目前关于跑步荷载模型的研究工作甚少，没有可用的跑步荷载模型，相关的基础性试验研究工作也非常缺乏。国外有学者采用类似跳跃荷载的“半正弦波”模型建立了跑步荷载模型[8]，但跑步荷载在频率、幅值、空间移动特性上与跳跃荷载有明显的区别，不宜直接使用。工程设计中常常用“有节奏荷载”的模型代表跑步荷载，然而“有节奏运动荷载”一般指健美操、舞蹈、节奏性跳跃或Bounce等，其对应的试验数据基础也与跑步荷载不同。

因此，本文通过试验收集了一批单人跑步荷载时程，建立了跑步荷载的傅里叶级数模型，给出了模型参数取值方法。进而开展了实际连廊结构跑步作用下的振动实测，对荷载模型的应用效果进行了检验。

1 跑步荷载试验

大量跑步荷载实测时程是建立荷载模型的前提。本研究采用Novel公司的Pedar高精度无线测力鞋垫技术开展了跑步荷载试验,如图2所示。测力鞋垫用于测量人在跑步时的足底压力，通过鞋垫内的分布式压力传感器实现，可以连续实时记录所受压力，并通过积分获得整体压力。测力鞋垫技术是一种新型试验手段，解决了传统固定测力板方式无法获得连续跑步荷载、也无法实现长距离测试的问题。

试验共有25名健康成年测试者参与，均为同济大学学生。试验前所有测试者均按照试验伦理要求签署了知情同意书。每位测试者共完成7组跑步工况的试验，跑步频率范围为2.4～3.6 Hz，间隔为0.2 Hz，对应的跑步速度为2.8～6.6 m/s。测力鞋垫的采样频率为100 Hz，每个工况重复两次。对于每个工况，试验志愿者都需在节拍器的引导下匀速连续跑步20 s以上，结束后需休息充分至无疲惫感才可进行下一工况的试验。

试验总共收集了345条有效连续跑步荷载时程，各工况有效荷载数据数量的统计信息如表2所示，各个工况数据量的均衡为荷载模型的准确性提供了保障。

(a) 现场情况

表2 各工况有效荷载数据数量统计

图3为某测试者在低频(2.4 Hz)、中频(3.0 Hz)、高频(3.6 Hz)工况时的跑步荷载名义力(竖向双足合力/体重)时程以及对应的傅里叶幅值谱。由图3可见，跑步荷载时程具有显著的周期性，中频率时频谱上前4～5阶峰值明显，分别对应于设定的跑步频率及其倍频。同时可以发现，在低频和高频工况，荷载的频谱有一定的“杂化”现象，各阶波峰呈现一定的宽度和“毛刺”，其对应的试验现象和背景是：受人体生理机能的限制，较低或较高频率，跑步者很难长时间准确按照节拍器的节奏跑动。

2 跑步荷载模型

2.1 傅里叶级数模型

基于第1章的观察，可将人的连续跑步过程视作为周期性过程，并采用傅里叶级数模型，即

(1)

式中：F(t)为竖向跑步荷载时程；G为人的静止重力；N为模型截断阶数；t为时间；rn为第n阶傅里叶系数，也称为动载因子(dynamic loading factor，DLF)；fp为跑步频率；φn为第n阶相位角。

可见，跑步荷载傅里叶级数模型是正弦函数的叠加，其用于结构动力分析是十分方便的。此外，现有很多设计规范中所推荐的人致荷载模型均为傅里叶级数模型。综上，本文采用傅里叶级数建立跑步荷载的模型。

2.2 模型阶数

合理的模型截断阶数N，即需要保证包含荷载的绝大部分能量，也应避免因阶数过高造成的模型参数取值困难和使用不便。基于上述原则，经综合分析全部的实测数据，建议取N=5，即考虑荷载的前5阶的贡献。这一取值与已有跳跃荷载(N=3)[9]和步行荷载(N=5)[10]，具有可比性。

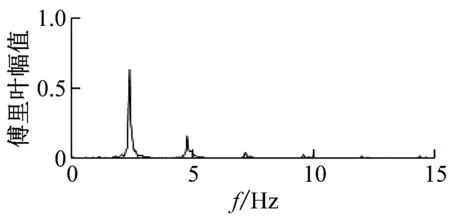
(a) 跑步频率2.4 Hz

2.3 动载因子计算原则

建立荷载模型的关键在于动载因子的取值，计算动载因子最常用的方法是峰值法和等效能量法(简称能量法)。峰值法是取跑步荷载傅里叶幅值谱上各阶谐波峰值处的幅值作为该阶动载因子FDL,n。由于测试者的连续跑步过程并非严格意义上的周期性过程，其傅里叶幅值谱上峰值附近范围内存在能量泄漏现象。峰值法忽略了泄漏的能量，仅仅考虑各阶谐波处的最大峰值，低估了跑步荷载值；而能量法将各阶谐波峰值附近所有能量集中在谐波频率作为动载因子，又高估计跑步荷载。因此，有学者[11]提出介于这两种方法之间的窄带分析方法，即将各阶谐波附近能量限制在一定带宽范围内计入模型计算，不考虑距离较远的能量，相对合理。因此，本文采用限定带宽的分析方法，并将各阶谐波附近能量扩散的范围取为(1.00±0.05)fp[12]。则第n阶主频附近计算范围内的能量为

(2)

式中：En为跑步荷载幅值谱的第n阶谐波附近计算带宽内的能量；fp为跑步荷载的频率；An(f)为跑步荷载傅里叶幅值谱的第n阶谐波附近计算带宽内的傅里叶幅值。则第n阶FDL为

(3)

2.4 动载因子计算结果

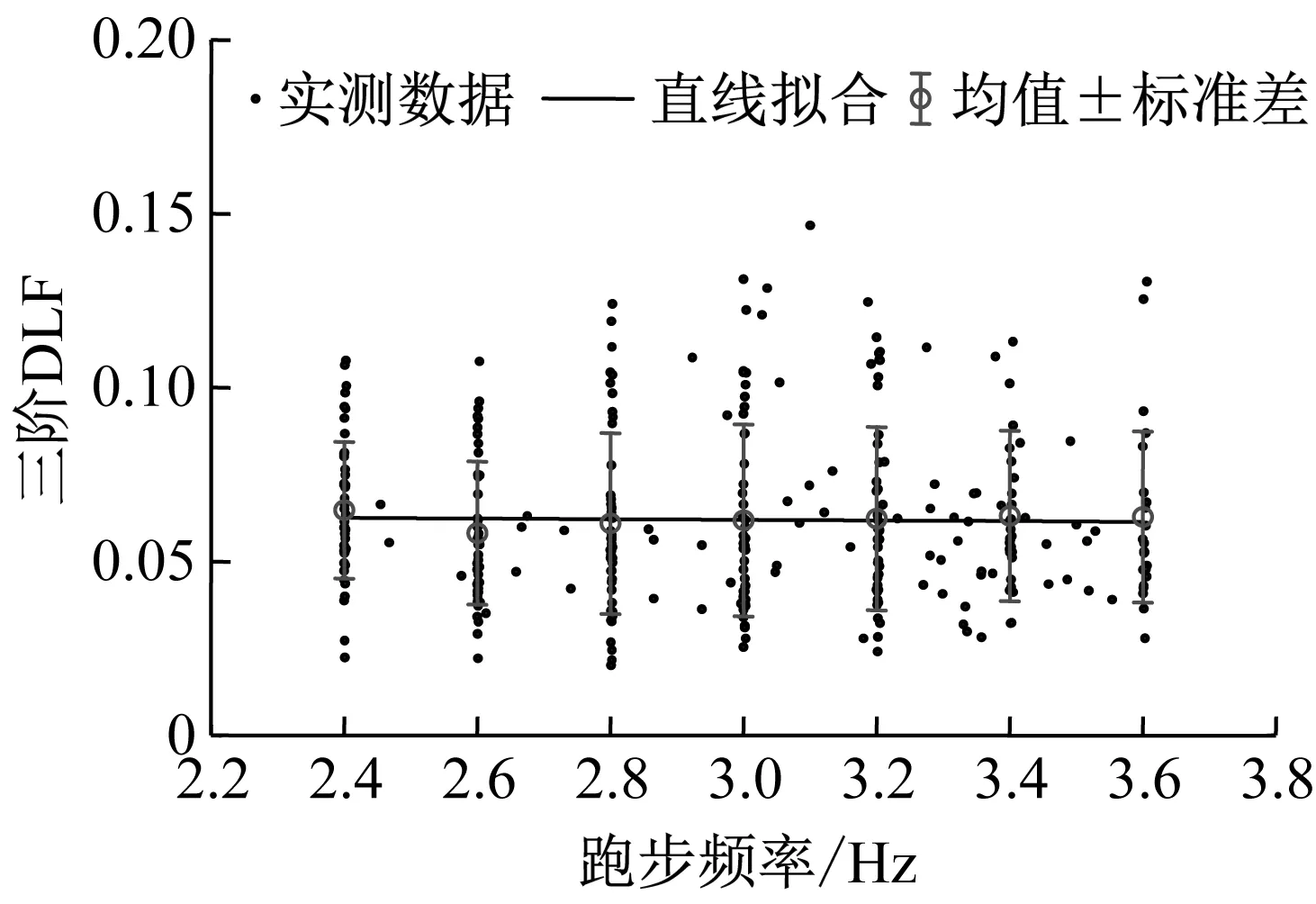
依据2.3节原则，首先将跑步荷载时程的长度截取为跑步周期的整数倍再求其傅里叶幅值谱，利用上述限制带宽法计算所有实测跑步荷载时程的前5阶动载因子如图4所示。

图4显示DLF随频率的变化比较离散。从与步行、跳跃等现有荷载模型一致的角度，计算7个频率工况下DLF的均值，并对其随频率的变化进行线性拟合，结果见图4。表3为前5阶动载因子在各个频率下的变化范围(括号内为均值标准差)，所得线性回归方程如表4所示。结果显示第1、第4阶DLF随频率增加而增加，第2、第3、第5阶DLF随频率增加而减小，与陈隽等研究中跳跃荷载DLF的变化趋势类似。

由于DLF的离散性较大，设计时可选用表4中的DLF均值回归方程进行初步分析，或表3中的DLF变化范围、均值和标准差进行精细化分析。

2.5 相位角取值

同样的，可采用2.4节研究各阶相位角随跑步频率的变化规律，图5所示为前5阶相位角随跑步频率的变化趋势。数据显示，各阶相位角的试验结果相当离散。由于人致结构振动通常是单模态主导，DLF值对响应最大值起决定性作用，相位角只影响最大值出现(或相对于外激励滞后)的时间。因此，本文采用目前常用的直接对各阶相位角取均值的方式，得第1、第3、第5阶相位角取π/12，第2、第4阶相位角取0°。

3 结构实测对比

3.1 连廊结构

某连廊结构如图6(a)所示，在该结构上进行单人跑步试验，将实测结构响应与采用第2章跑步荷载模型的计算响应进行比较，来检验荷载模型用于结构设计的可行性。该连廊为钢结构，材料强度等级为Q345，弹性模量Es=2.06×105N/mm2，平面尺寸为24.0 m×4.5 m，高度300 mm，连廊两端简支。经测试，结构自振频率为6.6 Hz，阻尼比为0.025。

(c)

(e)

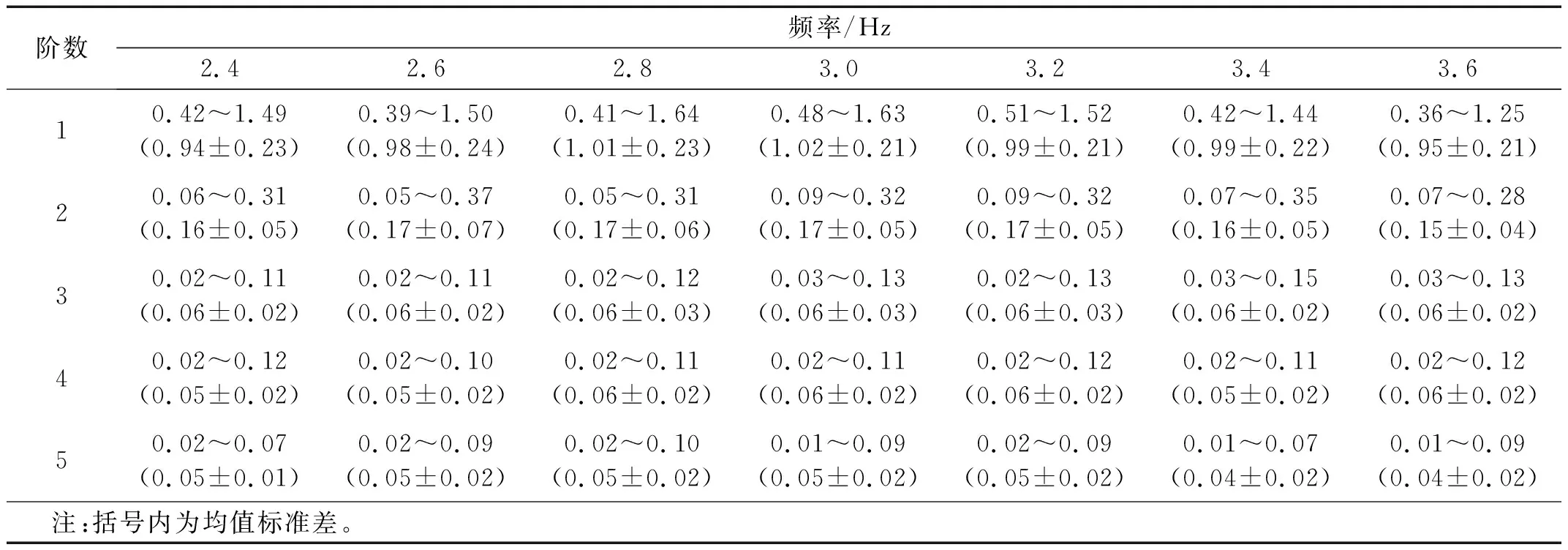
表3 前5阶动载因子在各个频率下的变化范围和均值、标准差

3.2 试验过程

测试者穿戴好测力鞋垫后，按照节拍器引导频率(如2 Hz，则为120 beat/min)在连廊上沿环形连续跑步30 s以上，以激发结构的稳态反应。同时，采用5个高灵敏度加速度传感器(LC0132T)记录连廊跨中等位置处的响应。测力鞋垫采样频率为100 Hz，加速度传感器采样频率为200 Hz[13-14]。试验现场和跑步路径见图6。

(a) 1阶相位角

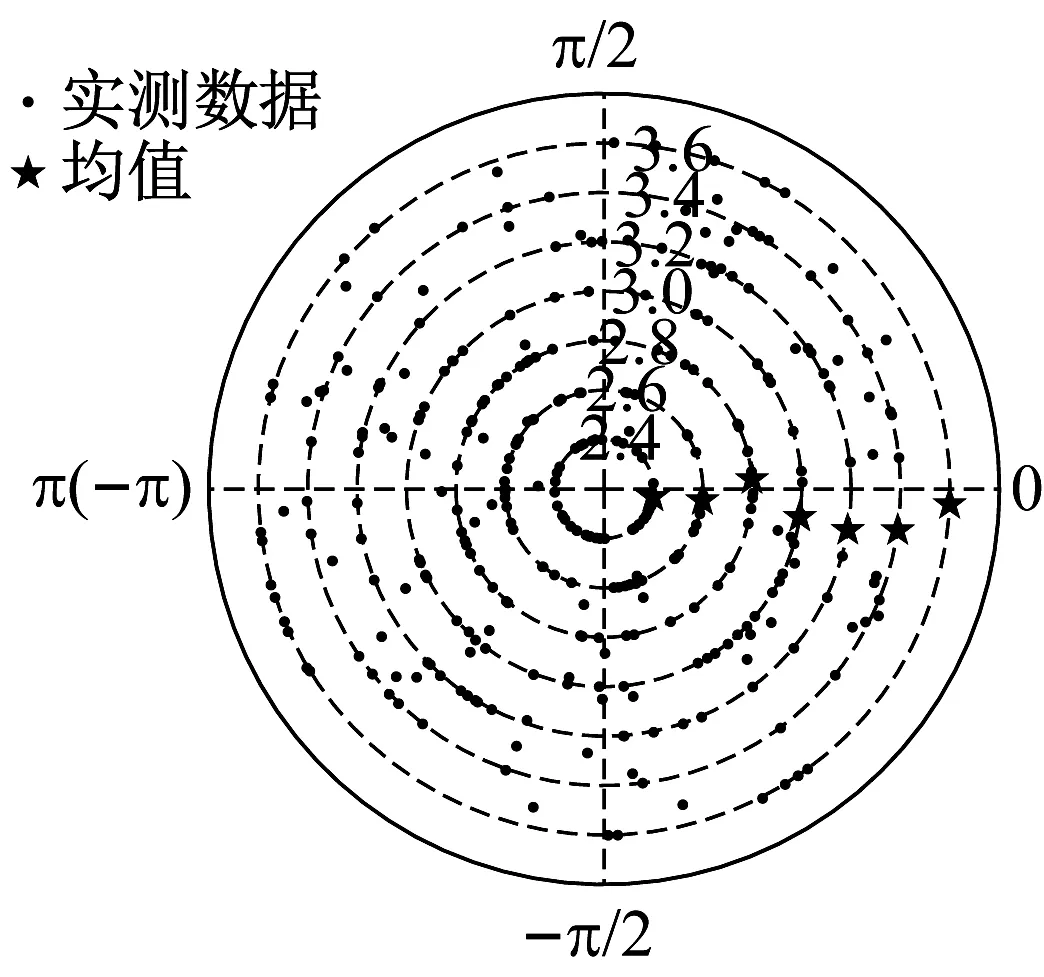
(d) 4阶相位角

表4 各阶动载因子回归方程

(a) 试验现场

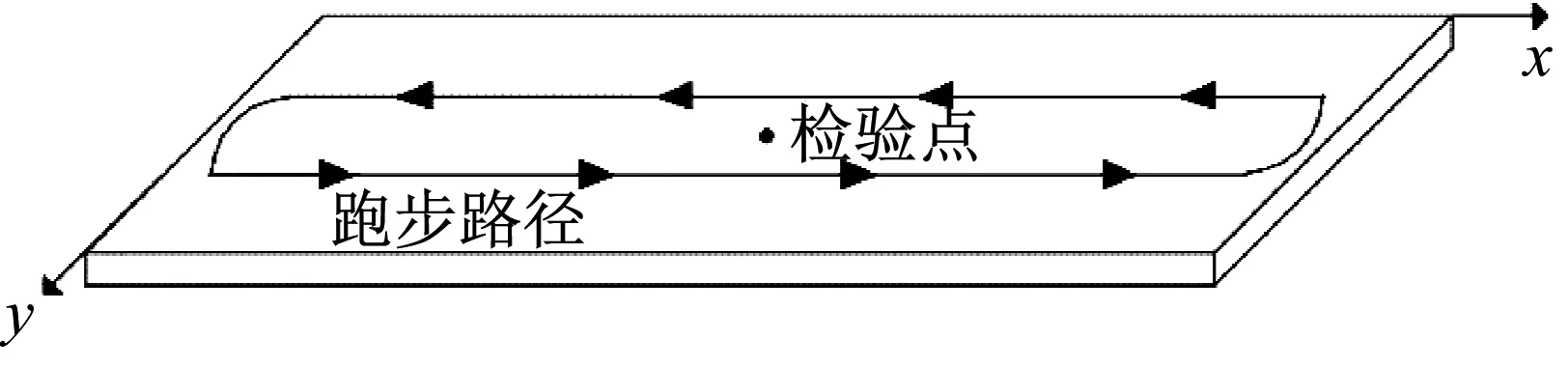
(b) 跑步路径及检验点

某测试者的体重为50 kg。按上述试验要求完成了5种跑步频率共12组的试验。图7为两次跑步频率为3.3 Hz时的跨中加速度响应时程，各工况结构跨中加速度峰值见表5。可以看出，当测试者的跑步频率为3.3 Hz时，荷载时程的第2阶谐波分量引发结构共振，此时的最大加速度是所有工况下的最大值，并且跑步频率越接近3.3 Hz，结构跨中加速度响应峰值越大。

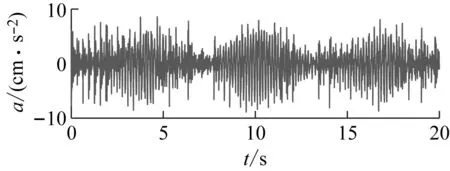
(a) 第一次

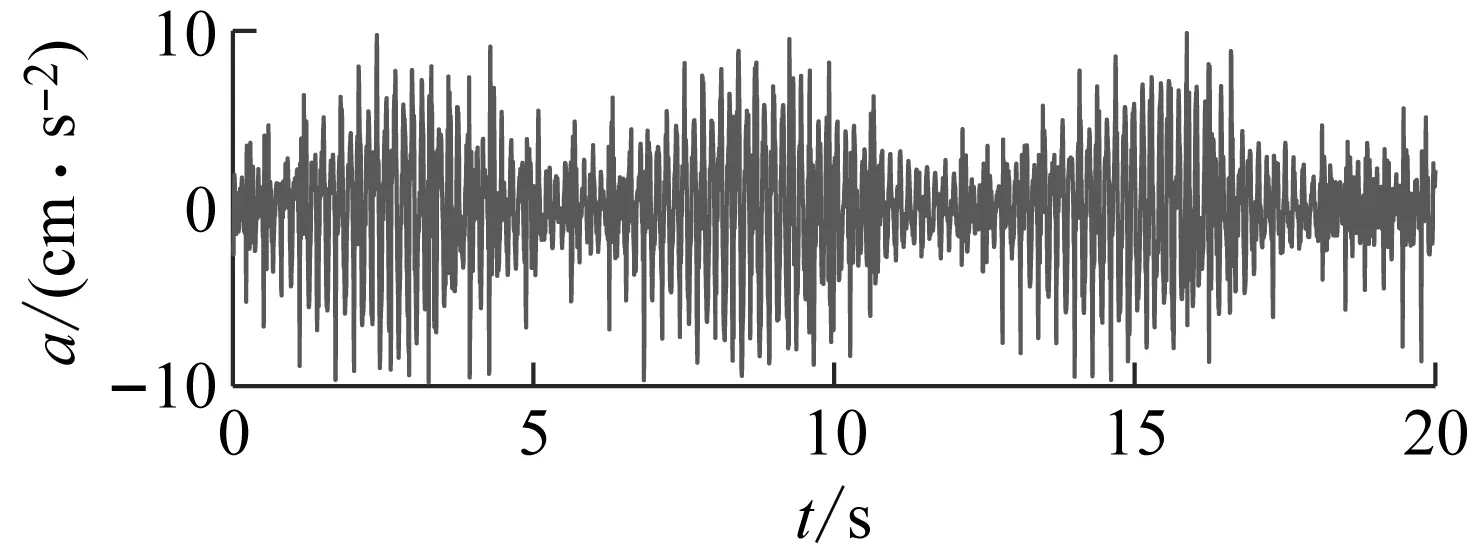
(b) 第二次

表5 不同频率跑步激励下连廊结构的实测最大加速度响应

3.3 数值模拟与试验结果对比

为验证所建荷载模型，首先对比模拟荷载时程与实测荷载时程。如图8所示，可见荷载时程的形状相似，幅值相差也较小。为进一步验证，建立连廊的有限元模型并计算结构在模拟荷载作用下的加速度响应，图9为连廊有限元模型及跑步路线示意图。模型基频为6.65 Hz，与实测基频6.6 Hz相近。计算不同跑步频率下DLF分别取均值、均值±标准差时连廊在模拟荷载作用下的跨中加速度响应峰值[15-18]，跑步频率增量取0.1 Hz，计算结果如图10所示，结构的实测加速度响应峰值与DLF取均值时的计算结果大体接近，且几乎都落在包络线(DLF取均值±标准差)内。

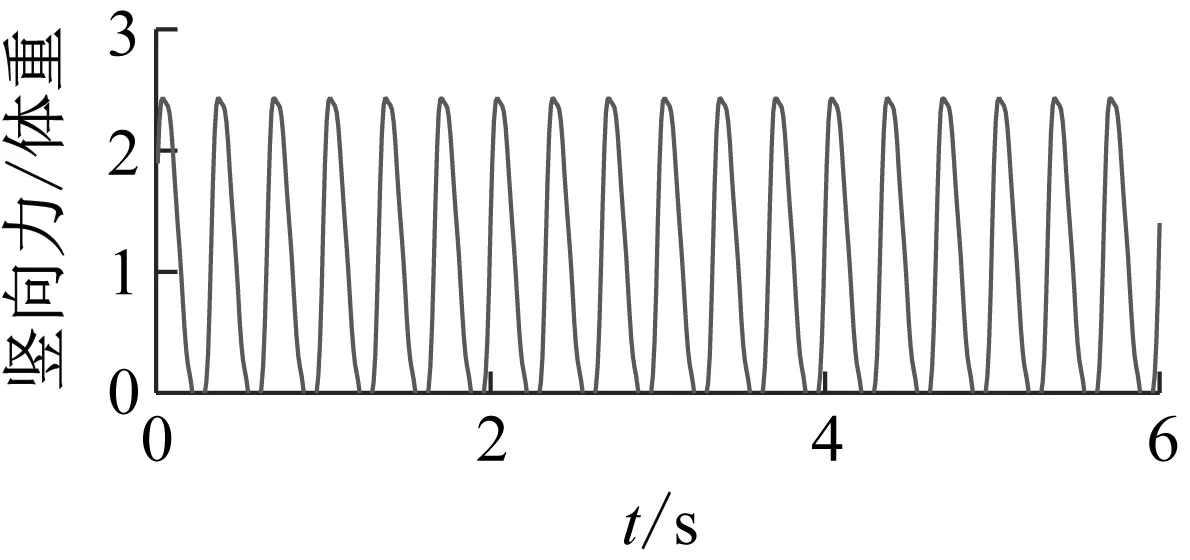
(a) 模拟3.0 Hz跑步荷载时程

(c) 实测3.0 Hz跑步荷载时程

图9 连廊有限元模型和荷载布置

图10 模型峰值加速度响应包络线与实测结构响应对比

此外，如果采用美国钢结构协会AISC规范Design Guide 11-1997所推荐的节奏性荷载，则对于2.75 Hz(该规范给出的荷载频率的上限值)，计算结果见图10中星号，比实测值大很多。对本例而言采用节奏性荷载代替跑步荷载是不合适的。由上述分析可得，本文提出的跑步荷载模型与实测荷载较为吻合，所引起的结构响应大体一致，可用于相关工程的设计与分析。

4 结 论

跑步荷载是室内、屋顶运动场以及人行桥等结构振动舒适度设计需要考虑的重要荷载类型。我国目前尚无跑步荷载模型。本研究利用高精度无线测力鞋垫技术开展了单人跑步荷载试验，并提出了傅里叶级数的荷载模型，由试验数据给出了连续跑步荷载的前5阶动载因子和相位角的建议值。通过将数值模拟与实际结构的响应对比表明，本文所建议的跑步荷载模型可供相关人致结构振动的工程设计与分析使用。