典型有偏估计方法均方误差极小值一致性分析
岳元龙 张彩虹 赵晓磊 韩云峰 左 信
(1.中国石油大学(北京)信息科学与工程学院;2.海洋石油工程股份有限公司;3.中海油研究总院有限责任公司)
在自动化等领域,y=Hx+w是一个重要的线性模型,广泛用于估计未知参数x,其中又以Gauss和Legendre在18世纪初提出的最小二乘估计最为经典。1900年,Markov提出Gauss-Markov定理和高斯最小二乘估计,并且证明了高斯最小二乘估计在线性无偏估计中具有最小的估计方差。
均方误差是衡量不同估计方法优劣程度的重要指标,估计均方误差越小,表示这种估计方法越好。 均方误差等于估计方差与估计偏差平方的代数和。 经典的高斯最小二乘估计是一种无偏估计,即偏差平方等于零,所以高斯最小二乘估计的均方误差就等于它的估计方差。 当数据出现复共线性时,此时最小二乘估计的均方误差会大幅增加,它不再是最优的估计方法。 为了解决这种问题,得到较小的估计均方误差,科研工作者提出了很多方法,其中,线性有偏估计是最直接有效的方法。 线性有偏估计通过引入较小的偏差,在均方误差准则[1~3]条件下,达到减小最小二乘估计方差的目的。 有偏估计不仅需要考虑方差大小,还要考虑偏差大小。 有偏估计优于最小二乘估计表现为有偏估计的均方误差小于最小二乘估计的均方误差。
线性有偏估计在近半个世纪以来发展迅速,科研工作者提出了不同结构形式的有偏估计。STEIN C针对Stein现象[4]提出James-Stein估计[5]。SCLOVE S L于1968年完善了James-Stein估计并提 出 压 缩 最 小 二 乘 估 计[6]。 HOERL A E 和KENNARD R W在研究回归问题中的岭分析及其应用的基础上[7],在设计矩阵中加入了一个偏参数, 提出最常用的有偏估计方法——岭估计[8,9]。LIU K J结合Stein压缩估计和岭估计的优点,对岭估计进行修正和改进,分别于1993年和2003年提出了两种新的较为常用的有偏估计方法——Liu估 计 和Liu 型 估 计[10,11]。 ÖZKALE M R 和KAÇIRANLAR S结合岭估计和Liu估计提出两参数估计[12,13],并在均方误差准则下证明,当观测矩阵存在复共线性时,它的估计效果是优于最小二乘估计的。 BATAH F S M等提出刀切广义岭估计和修正刀切广义岭估计,并在均方误差准则下得出 它 优 于 广 义 岭 估 计 的 条 件[14]。 2008 年,SAKALLIOLU S和KAÇIRANLAR S综合岭估计和带有先验信息的Liu估计,提出k-d估计类,并与Liu估计、 岭估计和两种特殊的Liu型估计进行比较, 得到新的有偏估计在均方误差准则下优于普通最小二乘估计、 普通岭回归估计和Liu估计[15]。DURAN E A和AKDENIZ F于2012年提出修正刀切广义Liu估计, 它是广义Liu估计和刀切广义Liu估计的组合估计, 并在均方误差准则条件下与广义Liu估计和刀切广义Liu估计进行比较,在均方误差准则下证明了修正刀切广义Liu估计优于广义Liu估计的一个充要条件[16,17]。 由于不同的估计方法有着不同的形式, 这给研究有偏估计的共同特性增加了难度,为此,岳元龙于2013年提出线性统一有偏估计,将不同的有偏估计方法用一种形式表示[18]。 2016年,刘佳瑞在岭估计的基础上考虑了齐次等式约束,提出综合条件c-K岭估计的方法,证明这种方法的有偏性[19]。 LIU G和YIN H于2020年在加权平衡损失下证明了椭球约束下的Gauss-Markov模型的可容许性[20]。 2021年,WANG L Y和CHEN T提出最小二乘估计的一种迭代算法,并基于岭估计原理推导出了岭参数的U曲线法[21]。
在工业研究中,更关注选择哪种有偏估计方法能更好地改善最小二乘估计。 因此,研究不同的典型有偏估计方法改善最小二乘估计方法的均方误差极小值的能力是否相同就显得尤为重要,如果相同,说明选用任何一种有偏估计方法改善最小二乘估计都是可行的;如果不同,则可选择具有最小均方误差极小值的有偏估计方法改善最小二乘估计。
在多种有偏估计方法中,广义岭估计(Generalized Ridge Estimation,GRE) 和 广 义Liu 估 计(Generalized Liu Estimation,GLE) 是对岭估计和Liu估计的推广,是两种应用比较广泛的典型有偏估计, 修正广义岭估计 (Modified Generalized Ridge Estimation,MGRE) 和 刀 切 广 义Liu 估 计(Jackknifing Generalized Liu Estimation,JGLE)则是先验信息估计类和刀切估计类中具有代表性的估计方法,线性统一有偏估计方法是现有的有偏估计方法 (Linear Unified Biased Estimation,LUBE)的统一表示形式。 因此,笔者选取这5种典型有偏估计方法进行研究。
1 线性估计模型及复共线性判断
1.1 线性估计模型
线性估计模型中估计未知参数的一般形式为y=Hx+w,其中,y是m×1维的观测矩阵,H是m×n维的观测矩阵,x是n×1维的未知参数矢量,w是与未 知 参 数x 无 关 且 满 足E(wTx)=0 和Var(w)=σ2I的相同分布的高斯噪声。 若HTH非奇异,此时最小二乘估计=(HTH)-1HTy。

1.2 矩阵复共线性判断
判断矩阵复共线性的方法有: 特征根分析法、条件数法、方差扩大因子法和行列式法。 本研究中判断矩阵的复共线性时选择的是条件数法。

2 有偏估计的一致性分析
本节选取GRE、GLE、MGRE、JGLE和LUBE共5种典型的有偏估计方法, 利用矩阵的分量形式进行典型有偏估计方法的均方误差极小值的一致性分析的理论推导。
2.1 GRE的极小值分析
GRE是在设计矩阵时通过引入偏参数矩阵KGRE来改善最小二乘的方差, 是应用最广泛的有偏估计方法。 GRE的典则形式表示为:
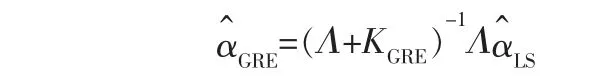
GRE的方差表示为:

将式(1)用矩阵分量形式表示为:

GRE的偏差表示为:

将式(3)用矩阵分量形式表示为:

GRE的均方误差用矩阵的分量形式表示为:

通过对式(5)进行求导,得到:


2.2 GLE的极小值分析


将式(7)用矩阵分量形式表示为:

GLE的偏差为:

将式(9)用矩阵分量形式表示为:

GLE的均方误差用矩阵的分量形式表示为:

GLE的均方误差取得极小值,表示为:
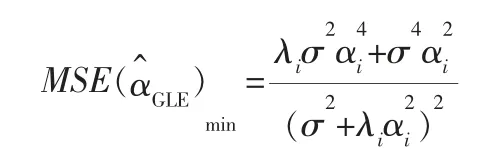
2.3 MGRE的极小值分析
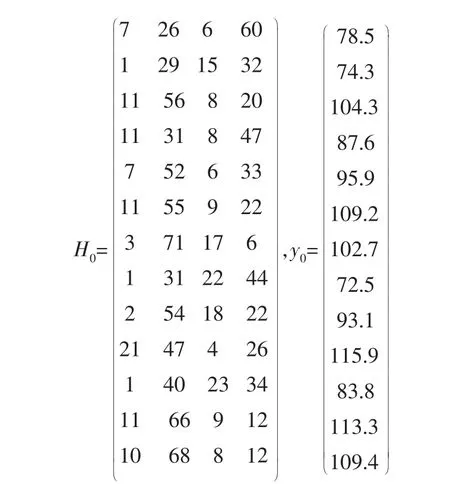
MGRE是在GRE的基础上添加了未知参数的先验信息b所产生的一种新的有偏估计方法。 假设先验信息b=,T=diag(ti),0 其中,KMGRE为偏参数矩阵。 MGRE的方差为: 将式(13)用矩阵分量表示为: MGRE的偏差表示为: 将式(15)用矩阵分量表示为: MGRE的均方误差用矩阵分量表示为: JGLE是一种综合了刀切估计和广义Liu估计的优点的有偏估计方法。 偏参数矩阵FD=diag(fi)=(Λ+I)-1(Λ+D),i=1,2,…,n,JGLE的典则形式表示为: JGLE的方差为: 将式(19)用矩阵分量表示为: JGLE的偏差表示为: 将式(21)用矩阵分量表示为: JGLE的均方误差用矩阵分量形式表示为: LUBE是在综合了多种有偏估计方法的基础上提出的估计方法。 最小二乘估计=(ZTZ)-1ZTy是针对ZTy进行的线性变换矩阵,其中ZTZ=Λ是一个变换算子。 所以,LUBE通过直接调整变换矩阵,也就是对角矩阵,提高最小二乘估计(LSE)的估计准确度。 LUBE的典则形式为(T)=。 LUBE的方差表示为: 将式(25)用矩阵分量表示为: 线性统一有偏估计的偏差表示为: 将式(27)用矩阵分量表示为: LUBE的均方误差用矩阵分量形式表示为: 在5种典型有偏估计方法的均方误差极小值一致性的理论分析的基础上,采用经典数据集进行数据分析,以更好地说明典型有偏估计的一致性。 1932年,WOODS H等在波兰进行水泥实验时产生的一组数据[22],是有偏估计研究应用最广泛的工程数据,1999年,KACIRANLAR S等在研究中再次使用该数据[23],这组数据是应用最广泛的工程数据。 本节也采用这组经典的数据集例子进行数据分析。 x1,x2,x3,x4分别代表水泥的4种化学成分,y0代表每1 g水泥所释放出的热量,h1,h2,h3,h4分别为热量与4种成分含量之间的关系,详见表1。 表1 波兰水泥热量与4种成分含量的关系 首先对数据处理如下: 参数向量x0的最小二乘估计为: 表2 数据的特征值及特征向量平方 表3 不同有偏估计方法的数据分析 图1a~e 分别是5 种典型有偏估计的方差(Var)、偏差(Bias2)和均方误差(MSE)的曲线。 可以看出,在偏参数为零时,有偏估计退化为最小二乘估计, 此时5种典型有偏估计方法的均方误差是相等的。 随着偏参数的增加,5种典型有偏估计曲线呈现相同的变化趋势,即偏差逐渐增加,方差逐渐减小,均方误差先减小后增加,但均方误差曲线都会出现一个极小值。 尽管5种典型有偏估计取得均方误差极小值时的偏参数不同,但它们的均方误差极小值是相同的。 说明不同的有偏估计方法改善最小二乘方差的能力是相同的,即典型有偏估计方法的极小值一致。 图1 5种典型有偏估计的指标曲线 由于每种有偏估计方法的均方误差与最小二乘方差的差代表它们改善最小二乘方差的能力, 虽然每种有偏估计方法呈现不同的结构形式,但每种有偏估计方法的均方误差都存在相同的极小值,即均方误差极小值与最小二乘方差的差是一个常数,这个常数不依赖于有偏估计方法的选择,这说明它们改善最小二乘的方差能力是相同的。 如果把最小均方误差作为有偏估计方法改善方差的能力指标,那么先验信息估计类的先验信息并不影响改善最小二乘方差的能力。 无论哪种有偏估计方法, 总能找到在某个偏参数时,均方误差取得极小值,此时有偏估计方法具有最优的改善最小二乘方差的能力。 因为典型有偏估计方法的最优估计效果是相同的,那么在实际参数估计问题的研究中, 若需达到最优估计效果,可以根据实际情况选取任意一种有偏估计方法进行参数估计。


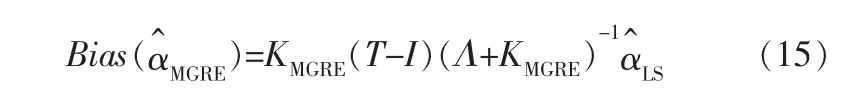



2.4 JGLE的极小值分析






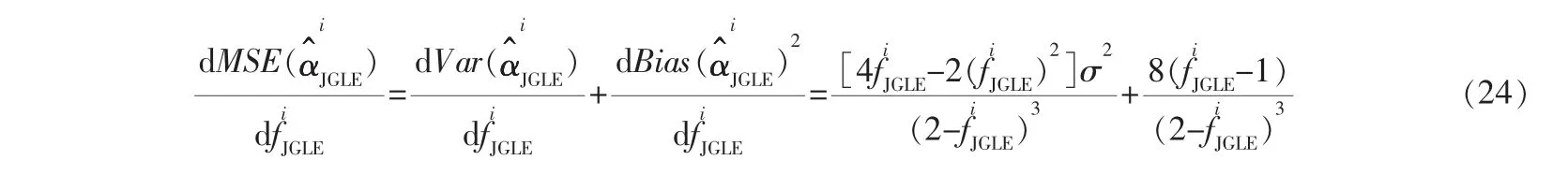

2.5 LUBE的极小值分析


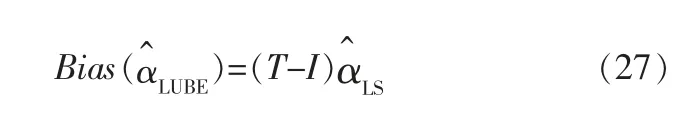

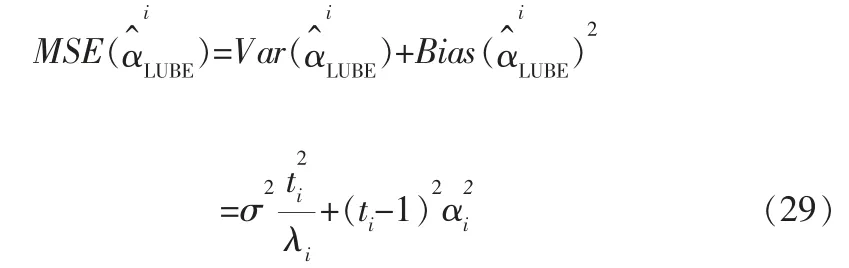


3 实例分析







4 结束语

