一题多解，培养发散性思维

筅辽宁省大连开发区第九中学 戴琳琳

1 引言

发散性思维是指大脑在思维时的一种扩散状态，它对创造力的形成具有直接影响.流畅、变通与独特是发散性思维的主要特征.解题教学中，引导学生从不同视角看待与思考问题，对学生解题能力的提升与发散性思维的形成具有显著的促进作用［1］.本文中，笔者以一道例题的解题教学为例，具体阐述如何在一题多解中培养发散性思维，为学生创新能力的形成奠定基础.

图1

2 发现隐含条件，明晰解题思路

数学解题时，不仅要有扎实的知识基础，还要有一双火眼金睛，能从题设条件中挖掘出一些若明若暗的条件，这些隐含条件往往对解题具有决定性的作用.不少学生在考试中解题失败的主要原因就是没有能发现题中潜存的隐含条件，导致走了很多弯路，致使解题时无从下手或想得过于繁杂.本题看似简短，但存在条件抽象、结构灵活的特点，教师首先应引导学生从题中的隐含条件（直角坐标系中的直角）的角度分析问题.

解法1：取线段AB的中点C，并连接PC.

解此解的核心是发现隐含的条件∠BOA=90°，而AB的中点就是外接圆的圆心；由∠POA=45°这个特殊角，可发现点P的坐标具有一定的特殊性；再从圆概念的内涵出发，很容易就联想到用方程解决此问题.此解题过程主要建立在对圆的概念有深刻理解的基础上，用这种方法突出清晰的思路与简便的计算过程.

3 夯实知识基础，筑牢解题根基

研究发现，中考中数学基础知识的占比非常大.在中考试卷中，一般不会有怪题或偏题等，基本以常规的科学记数法、图形、方程等为主，只要有扎实的基础与一定的思维能力，基本上不存在大的问题.解本题时，只要对求点的坐标的方法有一定的认识，学生基本上都能想到利用过该点作辅助线的方式解题.这种看似按部就班的解题方法，却对启发学生的思维具有重要作用，学生在解题中不断探索、前进，思维获得相应的成长.

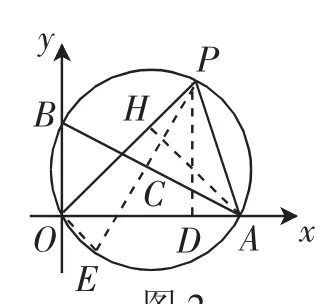
图2

求点的坐标最基本的方法之一是过该点作坐标轴的垂线.过点P作与x轴垂直的线段PD，或过点A作AH⊥PO，都是以这种基本解题方法为方向进行思考的.解题时，虽涉及了75°角的三角函数值，但对解题思路与结论并不产生影响.这种解题方法属于常规思维下的解题方式，符合大部分学生的认知规律，教师通过这种方式的引导，为培养大部分学生的发散性思维奠定了一定的基础.

4 形成数学思想，以不变应万变

教学向来都不是以会解题为最终目的，而是帮助学生获得终身发展的能力.数学思想是指人们对数学方法、内容或结构等的系统认识.很多教师遇到过这样的情况：学生的解题能力仅限于模仿的水平，一旦题设条件发生了变化，则无从下手.杜威认为：“高度概括并清晰的知识，才具备迁移的条件”［2］.想让学生形成灵活的解题与思维能力，首先要有良好的数学思想作为支撑.因此，新课标提倡我们要通过各种教学手段帮助学生构建新的数学思想，让学生在探索中形成良好的数学思维.

图3

对于以坐标系为背景的几何类题型，可将图形的基本结构作为思维的切入点，用一些基本图形的性质举一反三，达到以一通百的效果.本题中，过点P分别作两坐标轴的垂线后，就出现了学生所熟悉的正方形.从正方形的性质出发思考本题，问题则迎刃而解.同样地，换个角度，通过证明△APB是一个等腰直角三角形，与以上作正方形的原理一样，都是以不变的数学思想方法应付发生变化的问题，但解题的核心思想并没有发生改变.

5 利用数形结合，提升思维能力

利用数形结合，可将复杂的几何问题转化为简单的数量关系问题，也可将繁杂的数量关系问题简化为直观的几何问题，它最大的特点就是将问题变得直观、形象、通俗易懂.在初中，数形结合思想的运用一般与坐标系的建立、数轴、函数等密切相关，本题亦可从此角度思考，解题将变得直观、明了.

解法4：如图4所示，取AB的中点C，连接PC并延长与线段OA交于点H.站在函数的视角分析，点P为直线CP与PO的交点，已知直线OP的解析式为y=x.

图4

数形结合思想在初中数学中是运用得较多的一种数学思想，本题以函数图象为思维的切入点，再从代数的角度分析与解决问题.复杂的问题经转化后变得更为直观，容易理解.笔者发现，学生在运用该思想方法时，常会因为图形不标准、思维定式、逻辑不清等问题导致解题失败.因此，教师在用这种方法启发学生思维时，应充分了解学生的实际情况，要求学生严格按照条件准确画图，才能把复杂的问题变得简单化.

6 教学思考

数学这门基础学科消耗了学生不少的时间与精力，有些学生因鲜少在数学解题中收获成就感，而对学习渐渐失去信心.一题多解则能让学生在发散性思维中从不同角度观察与分析问题，多种解题方式中，总有一种方式是学生所擅长的，学生在丰富的解题方法中可感知到数学学习的乐趣，实现思维的步步登高，学习也不再那么单调.

一题多解会让学生不断地挑战自己的思维，体验非智力因素对学习的影响，并感知到数学学习的成就感.新课标提出：“教师要以不同形式的教学方式与探究活动，带领学生感知与体验数学的再创造过程，实现创新意识的提升.”［3］这就要求教师充分发挥学生的自主性，让学生在良好的情感体验中进行解题训练，以形成良好的解题技巧与技能.

同时，一题多解还能避免枯燥的重复练习，本题的四种解题方法，从不同的角度思考与分析，分别带给学生不一样的学习体验.众所周知，“双基”的掌握离不开一定量的实操，而一题多解完美地避免了反复演练带来的枯燥感.

总之，一题多解与发散思维的培养有着密不可分的联系.基础教育阶段开设数学学科的主要目的就在于发展学生的思维，而思维的发展又依赖于学生认知的发展.因此，我们应想方设法带领学生进入精彩的数学世界，让学生充分感知数学的丰富与多彩，体验数学独有的魅力，从而积极、主动地投身于数学学习中，在“多变”的数学中感知“不变”的真谛，让每个学生都能抛弃固有的思维模式，不断创新，成为自信且善于探究的新一代.