基于毕达哥拉斯模糊信息系统的多粒度冲突分析

王宣 陈跃

（六盘水师范学院数学与统计学院，贵州六盘水 553004）

1 选题背景及意义

冲突存在于社会的方方面面，因而关于冲突问题的分析与解决尤为重要。近年来，冲突分析这一旨在揭示冲突问题本质的理论应运而生，为冲突问题的有效解决开启了新篇章。基于学者们的潜心研究，产生了各种冲突分析模型。然而，对于一个实际的冲突问题，现有的冲突分析模型尚未结合多粒度粗糙集展开研究。实际上，在具体的冲突问题中（比如军事上的冲突），代理在做决策时是相当慎重的。换句话说，代理往往会采用多个评价函数去度量决策结果以免导致决策失误。因此，本文拟考虑从多粒度粗糙集的角度出发进行冲突分析研究。作为直觉模糊数的推广，毕达哥拉斯模糊数为描述不确定信息提供了新方向，毕达哥拉斯模糊数中的隶属度和非隶属度恰好可考虑用来描述冲突问题中代理对事件所持态度的程度。因此，本文拟基于多粒度粗糙集将毕达哥拉斯模糊集与冲突分析理论结合起来研究。

2 国内外研究现状

冲突在人类社会中是无法避免的。寻求冲突问题的有效解决策略是社会发展进程中必须攻克的难题之一。近年来，学者们致力于冲突分析的研究进而产生了很多模型［1-11］。对于具体的冲突问题，帕夫拉克（Pawlak）［1］最初构建了三值信息系统，其中分别用-1,0 和+1 来刻画代理对事件的三种态度。在不确定性背景下，模糊集和粗糙集成为研究冲突问题的两大主要工具。诸多学者将模糊集理论，粗糙集理论与冲突分析结合起来研究。如，王（Wang）等［2］构建了三角模糊信息系统上的三支冲突分析模型，进一步刻画并解决了冲突问题；杨（Yang）［3］等基于梯形模糊数的特点，将梯形模糊数运用到冲突分析的研究中，建立了梯形模糊信息系统上的冲突分析模型；张（Zhang）等［4］考虑到代理处于决策时的犹豫心理，将犹豫模糊数与冲突分析模型结合起来研究；孙（Sun）等［5］基于双论域上的概率粗糙集模型构建了三支决策框架，并提出了一种改进的Pawlak冲突分析模型；郎（Lang）［6］构建了基于三支决策的一般冲突分析模型。

20世纪下半叶以来涌现出很多数学理论以更好地描述不确定信息。模糊数学作为典型代表，为不确定信息的研究提供了向导。当我们无法对客观事物的类属划分做出确定的判断时，就产生了模糊性。模糊性在实际生活中不胜枚举。比如，胖与瘦、健康与不健康等等。然而，经典集合却对这些模糊概念束手无策。为弥补经典集合的缺陷，扎德（Zadeh）［12］于1965 年首次提出模糊集合的概念。自此之后，学者们提出了很多模糊集模型［13-17］。比如，粗糙模糊集［13］，韦格（Vague）-模糊集［14］，等等。此外，1986年阿塔那索夫（Atanass⁃ov）［15］首次提出了直觉模糊集的概念，耶格尔（Yager）［16］提出了毕达哥拉斯模糊集的概念，实现了对直觉模糊集的推广。结合具体的冲突问题，毕达哥拉斯模糊数中的隶属度和非隶属度可用来刻画代理对事件所持态度的程度。

粗糙集模型中的概念是基于单个二元关系来近似的。在许多情况下，我们往往需要根据问题解决的要求通过多个二元关系来描述特定概念。为此，钱（Qian）等［18］提出了多粒度粗糙集理论从而使得粗糙集理论得以更广泛地应用。在此基础上，学者们展开了很多关于多粒度粗糙集的研究［19-23］。如，梁（Liang）等［20］从多粒度的角度提出了粗糙特征选择算法，折（She）等［21］研究了多粒度粗糙集模型的结构。由于多粒度粗糙集是根据一族等价关系来近似的，这恰好可刻画代理在决策中的谨慎心理。因此，基于多粒度粗糙集将毕达哥拉斯模糊集与冲突分析结合起来研究将是一个有趣的课题。

3 预备知识

3.1 Pawlak冲突分析模型

Pawlak［1］最初为中东冲突构建了三值信息系统。下面回顾一下信息系统（ISs）的概念。

定义3.1一个IS即为四元组S=(U,A,V,f)，其中U={x1,x2,…,xs} 是一个有限对象集，A={a1,a2,…,at} 是一个有限属性集。其中是所有对象关于属性cj的取值集合且，f是从U×A映射到V的函数。

在定义3.1中，若U是一个有限代理集，A是一个有限事件集，V是所有代理关于事件cj的态度集合且，其中(i=1,2,…,s;j=1,2,…,t.)

此时，该模型被称为Pawlak信息系统上的冲突分析模型，且该IS被称为三值信息系统。

对某单一事件cj∈A，我们定义代理集U的三划分：

它们表示对cj持反对、中立和支持态度的代理集，也称为反对联盟、中立联盟和支持联盟。

例3.1中东冲突的三值信息系统如表1所示。

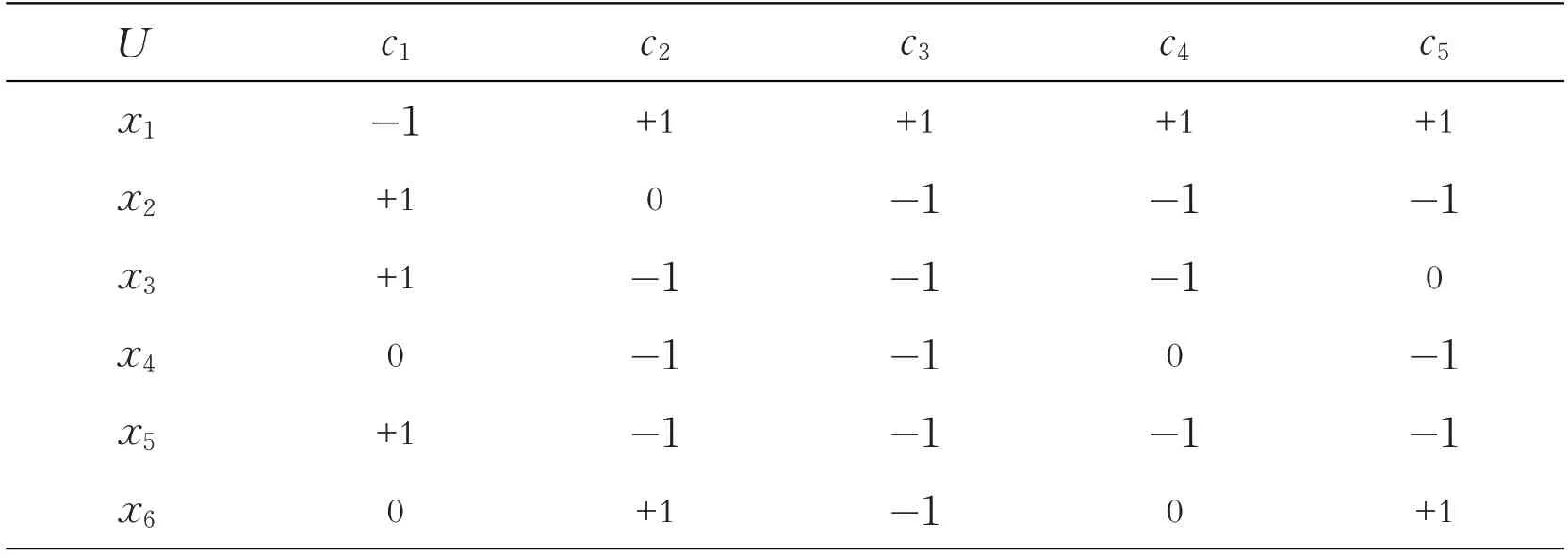
表1 中东冲突的三值信息系统

其中，x1,…,x6表示六个代理，c1,…,c5表示五个事件。下面用cj(xi)表示代理xi对事件cj的态度。如，c1(x1)=-1 表示代理x1反对事件c1；c2(x2)=0 表示代理x2对事件c2持中立态度；c1(x5)=+1 表示代理x5支持事件c1。

三值IS中用-1，0和+1描述代理对事件的三种态度。在实际的冲突情景中，同一代理对不同事件的态度往往存在不同程度的差异。例如，表1中c1(x2)=+1,c1(x3)=+1 表示代理x2和x3均支持事件c1。事实上，x2和x3的实际情况不可能完全相同。为此，本文考虑构建毕达哥拉斯模糊信息系统（PFISs）上的冲突分析模型以刻画代理对事件所持态度的程度。

3.2 多粒度粗糙集

多粒度粗糙集是基于一族等价关系而非单个等价关系来近似的，根据近似的要求不同，通常分为乐观多粒度粗糙集与悲观多粒度粗糙集两种模型。

多粒度粗糙集是根据一族等价关系来定义的。从某种意义上讲，多粒度粗糙集从多个角度来看待问题。结合实际的冲突情景，代理在决策时往往是谨慎的。换句话讲，代理需要通过运用多个评价函数来度量决策结果，这与多粒度粗糙集的思想不谋而合。因此，本文考虑展开PFISs上的多粒度冲突分析研究。

4 PFISs上的多粒度冲突分析

4.1 基于PFISs的冲突分析模型

在构建PFISs上的冲突分析模型之前，首先回顾毕达哥拉斯模糊数（PFNs）的概念。

定义4.1［16］若U是任一非空集合，则毕达哥拉斯模糊集P是一个具有下列形式

μij和νij分别表示代理xi对事件cj的支持程度和反对程度。其中

此时，该模型称为基于PFISs的冲突分析模型。相应地，该IS被称为关于冲突分析的PFIS。

对某单一事件cj∈A，我们定义代理集U的三划分：

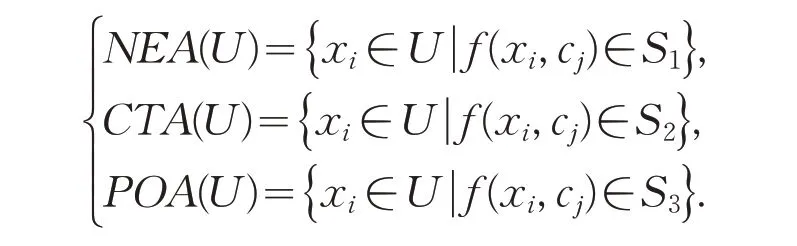
它们表示对cj持反对、中立和支持态度的代理集，也称为反对联盟、中立联盟和支持联盟。

注4.1（1）定义4.2中的S1,S2和S3可表示如图1所示：

图1 S1、S2 和S3

（2）特别地，对于下面四种特殊的PFNs给出如下定义：

a.P(0,ν)(0 ≤ν≤1)被定义成完全反对态度；

b.P(μ,ν)(ν=)被定义成弱中立态度；

c.P(μ,ν)(ν=被定义成强中立态度；

d.P(μ,0)(0 ≤μ≤1)被定义成完全支持态度。

例4.1中东冲突问题的PFIS 如表2 所示。下面用cj(xi) 表示代理xi对事件cj的态度。如，c1(x1)=P(0.2,0.4)∈S1表示代理x1反对事件c1；c4(x3)=P(0.3,0.4)∈S2表示代理x3对事件c4持中立态度；c5(x2)=P(0.8,0.3)∈S3表示代理x2支持事件c5。

表2 中东冲突的PFIS

注4.2（1）表2 中的PFIS 将作为全文的研究对象。此外，PFNs 的定义决定了表2 中的所有数据均在［0,1］之间。

（2）本节构建的PFIS 刻画了代理关于事件所持态度的程度。然而，在实际的冲突情景中，我们有时更关心代理对所有事件的总体态度。因此，接下来我们对此展开研究。

4.2 基于多粒度的三个联盟

基于表2 中的PFIS，接下来首先确定代理对所有事件的总体态度；然后，将总体态度映射成总体态度值；最后，通过贝叶斯决策过程计算出所需阈值以确定PFISs上的三个联盟。

4.2.1 总体态度

在确定代理对所有事件的总体态度之前，我们重新定义PFNs的加法与数乘运算。

定义4.3若P(μ,ν)是一个PFN，且k>0，则kP被定义为

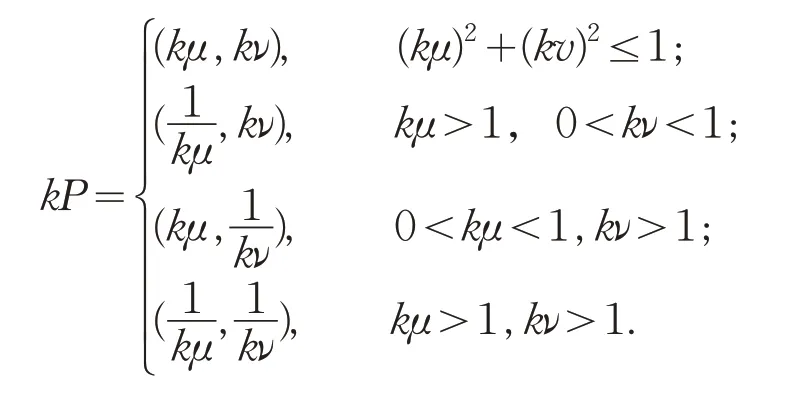
定义4.4若P1(μ1,ν1)和P2(μ2,ν2)是两个PFNs，则P1⊕P2被定义为

注4.3PFNs 的形式与向量类似，只不过两分量μ与ν满足0 ≤μ≤1,0 ≤ν≤1 且μ2+ν2≤1。基于此，考虑仿照向量的加法与数乘运算来定义PFNs的加法与数乘运算。

对于表2中的冲突问题，各事件关于各代理的重要性往往不同。换句话说，由于代理的实际情况不同，它们对各事件赋予的权重应该有所区别。为此，下面提出权重矩阵的概念。

定义4.5权重矩阵被定义为

其中ωij表示代理xi赋予事件cj的权重，且

基于定义4.5中的权重矩阵，下面确定代理对所有事件的总体态度。

定义4.6代理xi对所有事件的总体态度被定义为 (i=1,2,…,s;j=1,2,…,t.)

其中ωij表示代理xi赋予事件cj的权重，cj(xi)表示代理xi对事件cj所持的态度。

注4.4由cj(xi)是PFNs，ωij∈[0,1]，则根据PFNs的加法与数乘运算知也是PFNs。

下面将对表2中的PFIS继续展开研究以确定各代理对所有事件的总体态度。

例4.2（续例4.1）对于表2中的PFIS，假设权重矩阵为

表3 各代理对所有事件的总体态度(xi)

表3 各代理对所有事件的总体态度(xi)

4.2.2 总体态度值

为促进决策规则的形成，接下来构造两种函数将定义4.6中的映射成实数。在介绍第一种函数之前，首先需要定义PFNs到直线的距离。

细胞与细胞外基质形成动态力学环境，细胞内肌动-肌球蛋白收缩产生力，通过黏着斑传递给细胞外基质，在黏着斑处产生细胞牵引力[1-3]。细胞与细胞外基质之间的力学作用被认为是影响细胞黏附、迁移、增殖和凋亡等生物过程的关键因素[4-10]。研究细胞在弹性基底上产生的动态牵引力对于了解细胞如何感知周围环境力学性能变化具有重要的意义,因此，测量细胞牵引力是定量研究细胞迁移、收缩和分裂的重要方法。细胞牵引力非常小，大约为皮牛顿到纳牛顿量级，发生在纳米到微米尺度上[11]。

定义4.7 若P(μ,ν)是一个PFN，则P(μ,ν)到直线Ax+By+C=0 的距离d被定义为

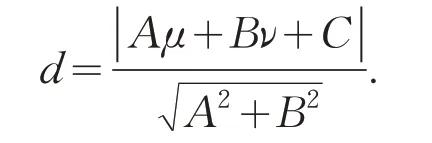
表4 各代理对所有事件的(xi)和(xi)

表4 各代理对所有事件的(xi)和(xi)

通过对表2中PFIS进行研究，现已明确各代理对所有事件的总体态度值。接下来，在定义4.2的基础上给出基于多粒度的三个联盟的概念。

定义4.101。（乐观）若S=(U,A,V,f) 是一个关于冲突分析的PFIS，且阈值α和β满足0 ≤β<α≤1，则基于乐观多粒度的支持联盟、反对联盟和中立联盟被定义为

2。（悲观）若S=(U,A,V,f)是一个关于冲突分析的PFIS，且阈值α和β满足0 ≤β<α≤1，则基于悲观多粒度的支持联盟、反对联盟和中立联盟被定义为

（2）在模型(S,α,β)中，算子和已分别在定义4.8 和注4.6 中被解释。换句话说，基于多粒度的三个联盟由阈值α和β决定。下面我们将根据毕达哥拉斯模糊理论提供一种计算阈值的方法。首先，构造适合本文模型的毕达哥拉斯模糊损失函数；其次，构造函数将期望损失映射成实数；最后，通过定理的形式阐述决策规则的形成过程。

定义4.11若S=(U,A,V,f)是一个关于冲突分析的PFIS，则毕达哥拉斯模糊损失函数被定义如表5所示：

表5 毕达哥拉斯模糊损失函数

根据表5中的毕达哥拉斯模糊损失函数，接下来提出期望损失的概念。

注4.9期望损失值刻画了期望损失的大小。事实上，

对于表2中的PFIS，构建毕达哥拉斯模糊损失函数如表6所示：

表6 表2的毕达哥拉斯模糊损失函数

由式（3），可计算得α=0.57,β=0.33,γ=0.44,则由定义4.10有基于多粒度的三个联盟如表7所示：

表7 基于多粒度的三个联盟

从表7可看出，在同一对阈值下，基于乐观多粒度的三个联盟与悲观多粒度的情形有很大区别。因此，分别从悲观多粒度和乐观多粒度的背景去研究代理集的三联盟是有意义的。

5 总结与展望

基于已有的冲突分析理论，本文构建了PFISs上的冲突分析模型。在该模型的基础上，为确定代理对所有事件的总体态度，首先，重新定义了毕达哥拉斯模糊数的加法、数乘运算并提出了模糊矩阵的概念。其次，通过定义两种评价函数将总体态度映射成实数。再次，本文提出了基于多粒度的三个联盟的概念。最后，通过贝叶斯决策过程给出计算阈值的方法。然而，以下两点问题需要进一步考虑：

（1）关于求解模型中的阈值。本文提出的毕达哥拉斯模糊损失函数中存在很多参数，导致阈值的计算公式较复杂。若能设计出计算阈值的算法将会是本文一大突破。

（2）关于总体态度值的确定。本文定义了两种评价函数将总体态度映射成实数。寻求其他合理的评价函数将毕达哥拉斯模糊数映射成实数将会是一个有意义的课题。