基于灰色马尔可夫链的铁路事故死亡人数预测模型

房 新，谈敏佳，吴啸宇，何 君

(南京理工大学 自动化学院，南京 210094)

铁路是我国交通运输方式的重要一环，保障铁路乘客和工作人员的人身安全是铁路运输的基本要求。铁路运输是一个复杂的系统，受到了人、车、路以及运行环境多方面的影响，预测事故和提前防范都十分困难。因此，文中针对铁路事故中的关键指标铁路事故死亡人数进行研究，使用灰色马尔可夫链模型对铁路事故死亡人数进行预测，分析未来一段时间铁路事故的发展趋势和状态特征，为铁路安全防范提供科学依据和参考，避免盲目性和被动性。

已有研究对交通事故进行预测大多采用宏观预测方法和微观预测方法。例如，机器学习预测[1]、BP神经网络预测[2]、贝叶斯预测及时间序列预测等，但都有一些局限性，导致预测结果存在较大误差。胡哨刚等[3]提出一种基于灰色理论的铁路一般事故数据预测模型，使用GM(1,1)模型对2015—2019年的小规模铁路事故数据进行预测，具有一定精度，但缺乏对波动数据的处理能力；纪俊红等[4]提出基于GSK-Adaboost-lightGBM的交通事故死亡人数预测，通过树类算法和集成算法，选取6种影响因素，对交通事故死亡人数进行预测，拟合精度较高，但参数的调试较为繁琐；Suna等[5]提出一种Light-GBM算法，这是基于Histogram的决策树算法，对于中等数据集的预测有着较好效果，但对于小数据集的预测精度较差；Hamad等[6]采用机器学习中的决策树方法对高速铁路车站中的事故进行分析，通过预测乘客特征和死亡人数，分析事故和增强车站的安全系统；林震等[7]运用贝叶斯预测法，将车速标准差作为预测指标，建立了车速和交通事故的预测模型，但在一些事故与车速没有明显关系路段不能正确构建车速和交通事故之间的关系；杨文忠等[8]采用一种基于时间序列关系的梯度提升回归树交通事故模型，提出了周期性的时序关系和多元周期时序关系来处理数据，但该方法存在一定的信息冗余，有时无法取得最佳处理结果。针对以上方法存在的不足，通过采用灰色马尔可夫模型对铁路事故死亡人数进行拟合和预测，通过预测铁路事故死亡人数判断铁路安全防护的状态和安全水平，为铁路安全运营提供超前的安全建议和参考。该模型既可以避免对铁路事故的关键因素进行划分，又可以适应数据波动，提高了铁路事故死亡人数预测的精确性、稳定性与可靠性，较好地反应了目前的铁路运行状况。

1 铁路事故死亡人数预测模型

2010—2020年，中国铁路快速发展，旅客发送量年增长率接近8%,年平均新增铁路里程0.55万km，年平均新增高速铁路里程0.33万km。随着铁路安全监管的不断加强，铁路事故死亡人数总体呈下降趋势，但2020年仍有674人死于铁路事故，具体如图1所示。

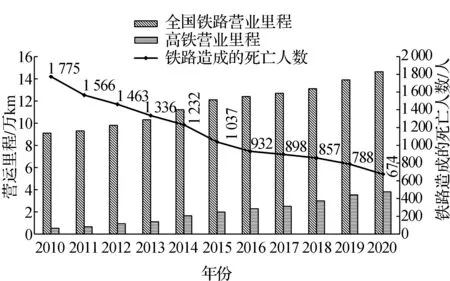
图1 2010—2020年中国铁路发展及事故死亡状况

1.1 基于灰色GM(1,1)的铁路事故死亡人数建模

灰色系统适用于预测复杂系统的变化规律和未来发展趋势，这些复杂系统往往受某些主导因素影响，例如，由人、车、路及环境共同影响的铁路运输系统[9-10]。其中灰色GM(1,1)是一个单变量的一阶微分方程，通过对铁路事故死亡人数的原始数据处理、建模、还原，得到铁路事故死亡人数预测。具体过程如下：

1)铁路事故死亡人数数据处理。获取某些年份的铁路事故死亡人数数据，将其作为原始序列

x(0)(t)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)}

t=1,2,…,n

(1)

对原始序列进行一次累加得到

(2)

x(1)(t)={x(1)(1),x(1)(2),x(1)(3),…,x(1)(n)}

(3)

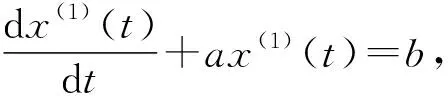
(4)

根据构造的矩阵求得参数值a，b为

(5)

3)灰色GM(1,1)模型建立。将参数带入微分方程，并将时间离散化，可得灰色GM(1，1)模型

(6)

(7)

4)铁路事故死亡人数预测值还原。运用得到的灰色GM(1.1)模型进行预测后，需要将得到的预测值进行累减处理并获得相对残差。对于灰色GM(1,1)模型来说，其使用条件与发展系数a的大小有关[11]，当a<-1时，灰色GM(1,1)模型的相对残差将超过20%，预测不宜采用GM(1,1)模型。若需要进行交通事故预测而灰色GM(1,1)模型的发展系数不满足条件时，可以从拥有的数据量出发对时间序列数据进行预测。当序列数据为小型数据集时(数据量小于100)，可以采用以马尔可夫模型为主的方法进行预测，并使用例如支持向量机等方法进行修正。当序列数据是中小型数据集时(数据量超过100)，可采用集成算法等经典机器学习或LSTM长短时神经网络进行预测。

1.2 基于灰色马尔可夫链预测模型

马尔可夫理论具有无后效性，在对随机过程的研究中，它认为系统的未来状态只与当前的状态有关。灰色GM(1,1)模型预测铁路事故死亡人数时，模型会将波动的数据视为干扰，而波动数据是在铁路运输过程中随机耦合产生，直接剔除会大大降低模型的精度，因此，对于一些铁路数据异常的年份，预测会产生较大误差。采用马尔可夫模型可以弥补灰色模型对于波动数据处理时的不足，利用其对于处理波动性数据的优势，对灰度预测结果进行修正[12-13]，提高铁路事故死亡人数预测模型的抗干扰性和准确性。建模过程分为以下3个步骤。

1)灰色GM(1,1)预测模型的状态划分。采用模糊理论的方法对灰色预测模型的状态进行划分，一共划分为i个状态，每一种状态表示为Si(i=1,2,…,n)，划分的状态表示未来铁路事故死亡人数预测的一种变化趋势，准确预测、高估及低估等。通过创建三角模糊数,代入相对残差Xt得到相应αsi(Xt)[14-15]，对于模糊状态划分矩阵G需要满足如下条件

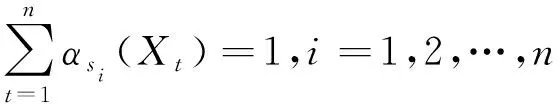
αsi(Xt)∈[0,1]

(8)

(i,t=1,2,…,n)

(9)

2)灰色GM(1,1)预测模型的状态转移矩阵。根据创建模糊状态概率矩阵，计算概率转移矩阵。定义Cjk为状态Sj到状态Sk的模糊转移频数，Bi为所有数据落入状态Si的频数，算式为

(10)

(11)

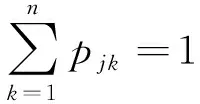
(12)

得到马尔可夫状态转移矩阵为

(13)

3)计算i+1年的预测值在各状态上的分布。根据第i年预测值所处状态的概率分布Qi(通过将相对残差带入三角模糊数中求得)与状态转移矩阵P，得到预测年份的状态分布

Qi+1=Qi·P

(14)

设各个状态的区间端点为ai(i=1,2,…,n)，则相对残差的预测值为

(15)

根据得到的预测年份相对残差对灰色预测的预测值进行修正，得到灰色马尔可夫模型的预测值。当相对残差预测值为正时算式取负号，反之取正号。

(16)

2 案例分析

文中选用2010—2020年中国铁路事故死亡人数数据进行建模，对其中2010—2019年数据进行拟合、2020年数据进行检验，最后通过铁路事故死亡人数预测模型对2021—2023年情况进行预测，并给出管理建议和方法。

2.1 灰色GM(1,1)铁路事故死亡人数预测模型案例分析

铁路事故死亡人数数据如表1所示。在建模前需要对数据进行光滑性验算、级比验算和准指数验算，通过计算可以看出数据同时满足光滑性条件、准指数条件和级比条件，可以开始构建GM(1,1)预测模型。

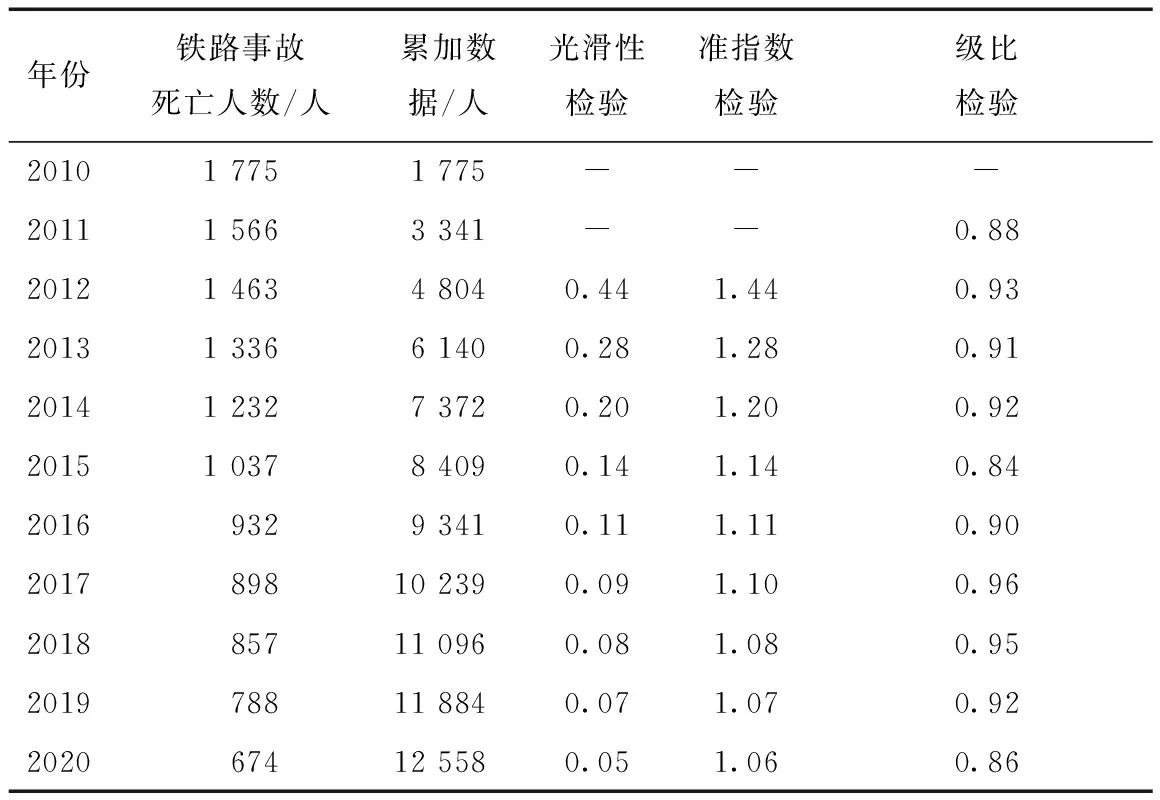
表1 2010—2020年铁路事故死亡人数及检验结果

由式(5)使用最小二乘法可得参数a=0.092 6,b=1 818.34，由式(7)可知GM(1,1)模型为

将t=10带入预测模型，可得2020年预测的铁路事故死亡人数为686人。通过该模型所得到的所有预测结果如表2所示，计算各个年份的残差和相对残差。

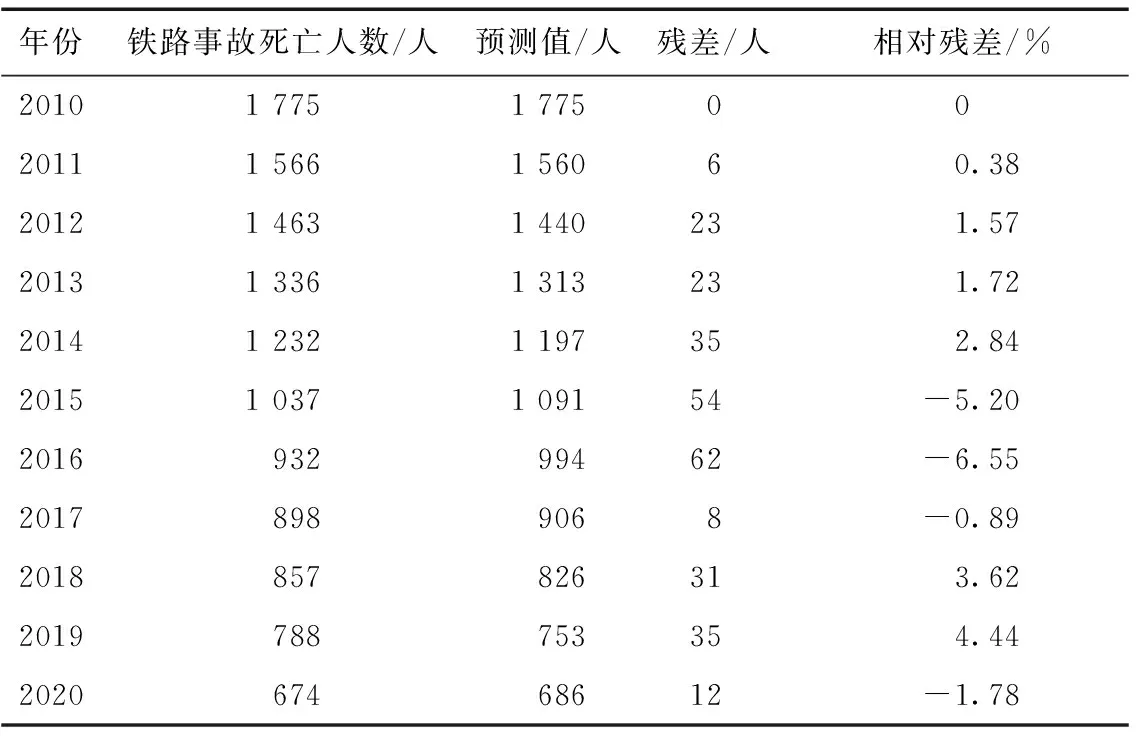
表2 GM(1,1)预测结果分析

由表2可以看出，灰色GM(1,1)模型对于2010—2020年中国铁路事故死亡人数估计有着较好的预测结果，模型预测的最大相对残差值为-6.55%，最小相对残差为0.38%，平均相对残差为2.90%(取绝对值进行运算)，可以较好地拟合给出的数据。对于2020年的预测数据，其相对残差为-1.78%，低于平均相对残差，说明此模型对于短期的预测精度相对较高。

由图2(相对残差取绝对值绘制)可知，在一些数据波动年份，灰色GM(1,1)模型的预测还存在较大波动。在2015—2016年，相对残差值分别达到了-5.2%和-6.55%，在后续的马尔可夫状态划分时，这两年的状态属于状态S1，表示预测的铁路事故死亡人数较真实值偏大，真实的事故死亡人数低于预测值。总体看，模型的预测精度较高，但对一些随机波动的数据预测精度下降，因此，下文采用灰色马尔可夫模型对预测结果进行修正。

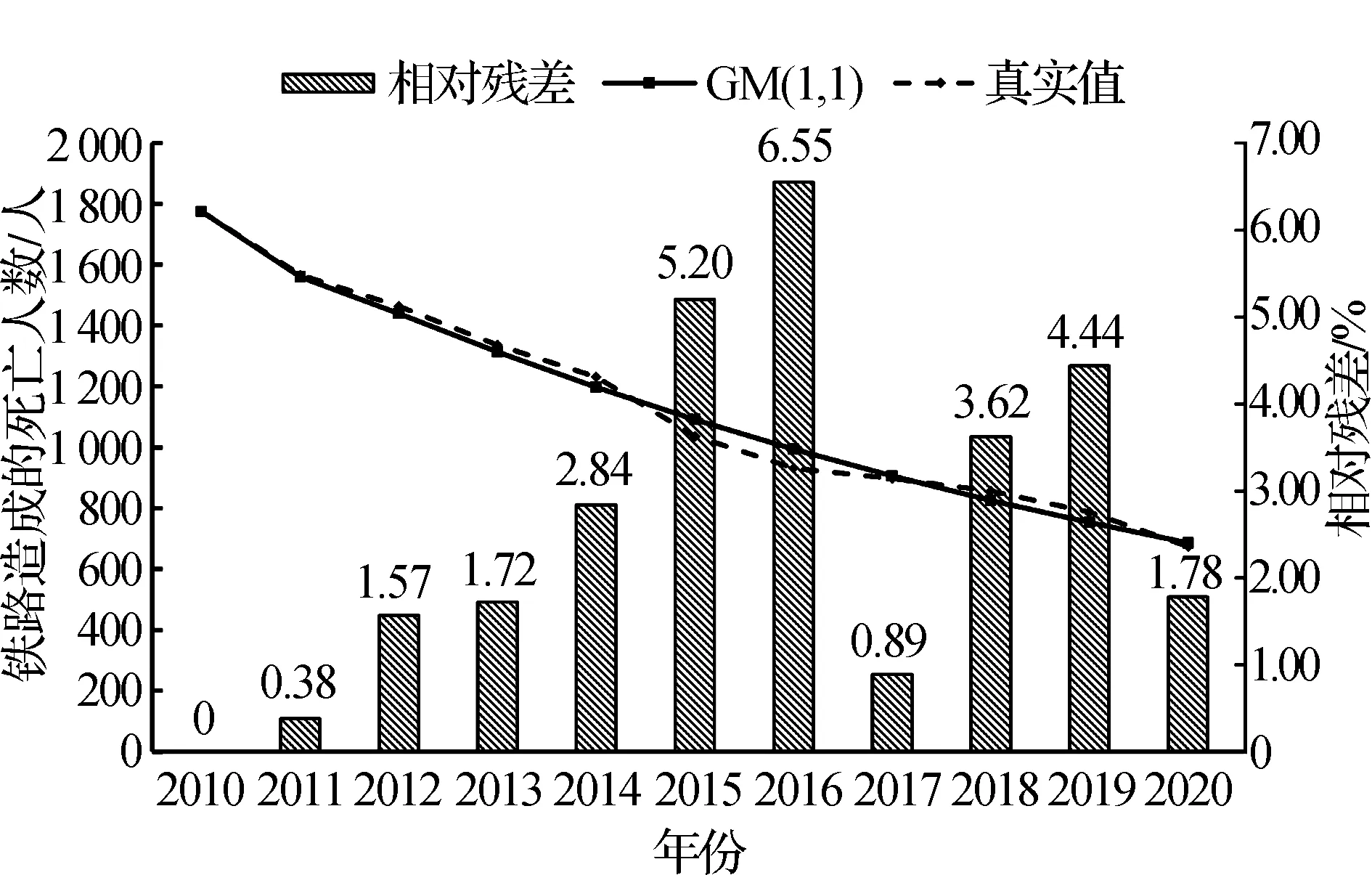
图2 GM(1,1)预测结果及相对残差

2.2 灰色马尔可夫链预测模型案例分析

针对GM(1,1)模型在处理波动数据时的缺陷，采用马尔可夫链对灰色预测结果进行修正，提高预测输出结果的精度。进行修正前，需要对马尔可夫状态进行划分，根据GM(1,1)预测模型的相对残差作为划分依据来创建三角模糊数。由灰色GM(1,1)的性质可知，其预测值的相对残差需要小于10%时才能满足预测的精度要求，所以第一个边界点的绝对值取0.10，第二个边界点需要将数据靠近数据边界，且包含所有数据，而预测值的相对残差绝对值的最大值为6.55%，通过取整，边界点的绝对值取0.07，具体模糊数算式为

(17)

将灰色GM(1,1)的预测值代入上述隶属函数中，可得到各个年份在3种模糊状态下的概率，当预测值在某一个状态下的概率值最大时，便认为此时它处于该状态，结果如表3所示。可以看出，在状态S1时，预测值的相对残差较大且为负值，说明此时预测的铁路事故死亡人数要高于实际值，此时处于高估状态；在状态S2时，相对残差接近于0，说明此时铁路事故死亡人数的预测与真实值相吻合，此时处于正常估计状态；在状态S3时，系统预测的相对残差为正，说明此时铁路事故死亡人数的预测值偏小，实际铁路事故死亡人数会高于预测值，此时处于低估状态。

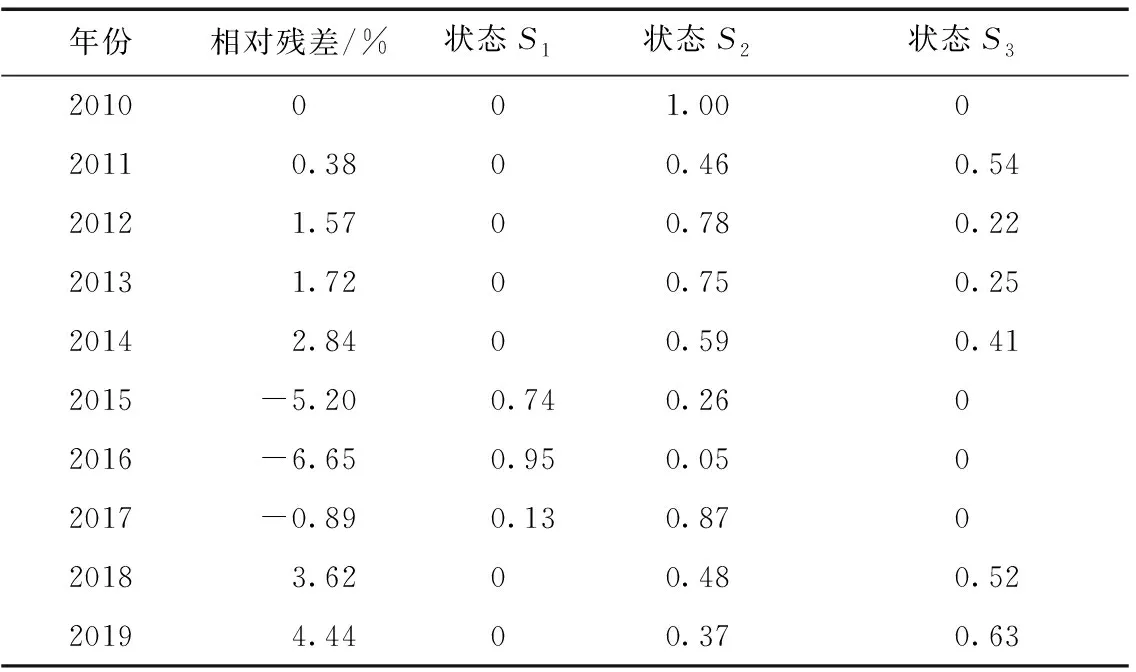
表3 马尔可夫状态划分

由表3数据，根据式(10)～(12)得马尔可夫状态转移矩阵

由式(14)得2020年铁路事故死亡人数预测值在模糊状态中的概率分布为

由式(15)可得2020年铁路事故死亡人数相对残差预测值为

由式(16)可得灰色马尔可夫模型对2020年铁路事故死亡人数的修正值为

使用灰色马尔可夫模型进行修正后的2020年铁路事故死亡人数为680人，此时相对应的残差为-0.9%，比灰色GM(1,1)模型进行估计时的相对残差下降50%，预测结果处于S2状态，表明预测值估计准确。为避免模型的偶然性，对2019年的铁路事故死亡人数预测值进行修正,结果表明，使用马尔可夫修正后2019年的铁路事故死亡人数为760人，相对残差为3.4%，精度提高了1%，说明当灰色GM(1,1)模型预测值偏小时，马尔可夫模型仍然可以进行一定程度的修正。因此，使用灰色马尔可夫铁路事故死亡人数预测模型对2021—2023年的铁路事故死亡人数进行估计，具体的预测结果如表4所示。

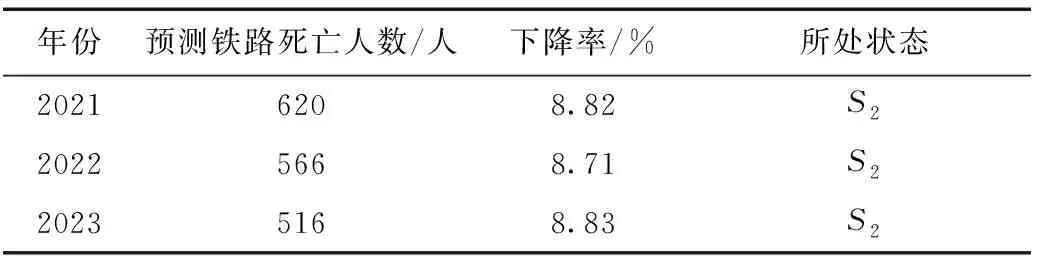
表4 2021—2023年预测数据

根据预测结果可知，2021—2023年铁路事故死亡人数预测均处于S2状态，年铁路事故死亡人数下降率高于8%但低于9%，表明铁路事故死亡人数的预测值与实际值接近，处于平稳下降阶段，但铁路安全运营还有提升空间。铁路部门通过派出检查组和发放问题整改通知书两种较为常规的检查手段进行监管，根据2014—2019年铁路部门派出检查组和发放问题整改书数据，分析监管措施与当年铁路安全运营之间的联系(见图3)。

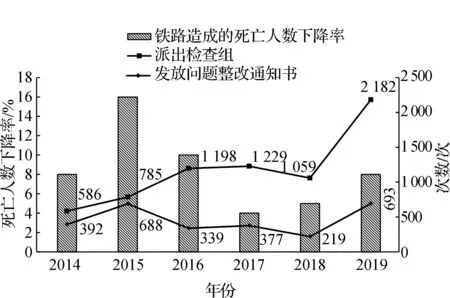
图3 铁路部门检查频率与事故关系

2014—2016年，随着铁路部门派出检查组次数的持续增加，铁路事故死亡人数的下降速度明显放缓，2015年相较于2014年铁路事故死亡人数下降16%，2016年下降10%。2017—2018年，随着铁路部门派出检查组次数稳定在1 100～1 200次，铁路事故死亡人数的下降率仅维持在5%以下，当2019年提高派出检查组次数到2 182次后，下降率提高到8%。说明通过增加铁路检查组的检查次数，可以较好提升铁路运营的安全意识，如果可以在检查过程中及时对发现的安全问题发放问题整改通知书，将其与检查次数维持在一个较为接近的水平，可以更好地督促铁路运营，有利于发现问题、解决问题，提升列车运行的安全性。

2021—2023年，新冠疫情依旧会对铁路运输产生一定影响，为保证铁路运行的安全可靠和铁路事故死亡人数持续降低，铁路部门需要构建一个高质量的安全保障体系[16]。一方面铁路监察部门需要继续加大检查力度，对违反安全运行的行为加大惩罚力度，同时借助大数据和智能巡检的帮助，对列车状态、人员操作及运行环境多方面因素进行监督。另一方面，铁路部门需要投入资金，积极制定日常操作的技术标准和安全检查技术创新，建立完善的铁路信息数据库，将更多的关键因素纳入到铁路事故的考虑范围内[17-18]，为今后取代人工检查组做好技术准备。只有当铁路部门的监察、惩戒、创新三方面的措施博弈到一种均衡状态时，铁路客运才可能健康长久地发展[19-20]。

3 结 论

1)灰色马尔可夫链模型在进行铁路事故死亡人数预测时，可以满足稳定性和精度的要求。使用模型对未来3年的铁路事故死亡人数进行分析,可以得到未来短期内的安全运营状况，并提出安全建议措施。

2)灰色马尔可夫链模型可以在少量数据的情况下进行建模预测,实用性强，但无法考虑到其他多方面因素的影响和突发条件下的不确定因素,存在一定的滞后性和缺陷。

3)铁路运营的安全状况与一些其他影响因素也有联系，需要进一步提取出一些关键影响因素，后续可以构建出一种反应更快、更加综合的预测模型。