疫情下安装共享电动车头盔消毒装置博弈

梁顺利，李香红，李大韦，郑兰兰，宋晖颖

(1.河南理工大学 能源科学与工程学院， 河南 焦作 454003； 2．东南大学 交通学院，南京 211189)

在低碳出行、解决最后一公里的大背景下，很多城市投入了共享单车，随着便捷性要求的增长，共享电动车也走进人们的视线，众多学者进行了相关问题的研究[1-6]。从前瞻性角度来看，丹麦等国外学者对头盔的保护效果及政策进行了研究[7-9]，同时我国也推行了“一盔一带”政策，相信未来会有更多的共享电动车运营企业配备头盔。但随着新冠疫情爆发，通过对不同措施的防疫效果进行分析发现[10]，共享类物品的卫生安全问题受到了人们的广泛关注，头盔消毒问题也成为关注热点。目前共享电动车头盔消毒多数采用定时、集中、批量的消毒措施，初步实现人工管理[11], 但无法实现使用后的及时消毒，大面积的消毒无法顾及到细节，而头盔相对空气流通性较好的车把、车身等部位[12]更具有密闭性以及口鼻密切接触性的特点，更易发生病毒传播。虽然现在并无相关企业安装相应消毒设备，但随着需求的不断增加，安装相应消毒设备将纳入企业考虑范围。研究表明，在环境适宜条件下，某些变异病毒在塑料表面存活72 h后依旧具有传染性[13]，短时间内根本无法自行死亡。针对共享电动车头盔仍存在消毒不及时问题，蔡玥[14]、惠英等[15]在新冠疫情背景下研究了共享单车的卫生及使用情况。王惠队等[16]通过对重大公共卫生事件下出行行为的研究发现，共享单车更符合群众在短距离出行条件下的需求。所以，解决好共享电动车头盔消毒问题十分关键。

在新冠疫情背景下，文献[17-19]从博弈角度分析了中外之间的贸易相关问题，国内学者[20-24]以及国外研究人员[25-28]也利用博弈论解决了许多企业与政府之间的问题。自驾摩友及外卖送餐人员也在每天对自己的私有头盔采取消毒措施[29-30]，如何通过安装共享电动车头盔消毒设备保障政府和企业利益最大化、减小因使用共享电动车造成新冠疫情传播风险，已成为当前研究的主要内容。

综上，针对新冠疫情下企业与政府间在博弈过程中是否会考虑安装头盔消毒设备问题进行讨论，以便实现新冠疫情背景下政府及企业的收益最大化。政府通过监管企业安装头盔消毒设备来降低人们的感染风险，从经济角度出发，降低了人们的感染风险，也就减少了政府的支出。而企业也可能因安装相应的消毒设备，满足人们出行的防疫需求，进而增加用户，带来额外收益。因假定双方存在非合作的利益冲突，可以使用完全信息博弈。通过建立博弈模型对演化博弈结果进行分析，得出能够使双方收益最大化的条件，实现人们健康出行，减少因使用共享电动车而造成新冠疫情的传播。

1 建模假设相关问题描述

市场共享电动车的运营，围绕着企业的收益进行相关规划，当企业安装消毒设备时，出于更加卫生的角度，必定会吸引潜在客户选择本企业的出行车辆，但同时也会产生安装及维修成本的增加。当本企业不安装，另有企业安装时，会失去部分原有客户，造成收益减少。对政府来说，如果不进行监管，政府则不用支付相关监管费用，但若造成新冠疫情的传播必会产生新的相应损失；如若进行相关监管，则要额外支付监管费用，但同时由此造成疫情传播的风险会大大降低，造成的相应损失也会减少，并且如果企业不进行安装，则政府有权对其进行相应惩罚，可以通过惩罚不安装的企业带来额外收益。

1.1 参数设计

假设企业和政府都为理性“经济人”，都追求最终利益最大化。企业与政府都在完全信息条件下进行博弈，参数设计及含义如下所示。

C：安装相应设备的成本及后期维修成本；

W0：企业正常情况的收益；

W1：安装后的增加收益；

W2：不安装时损失的市场收益；

F0：政府监管需要的花费；

M：在政府监管下企业没有安装设备时受到的惩罚；

N：企业不安装且政府不监管产生的社会危害(由政府承担)；

D：企业不安装但政府监管产生的社会危害(由政府承担)。

1.2 博弈收益矩阵

在企业与政府监管及安装博弈中，企业选择安装(x1)的概率为p，选择不安装(x2)的概率为(1-p)；政府选择监管(y1)的概率为q，选择不监管(y2)的概率为(1-q)。因此，得到相关收益矩阵如表1所示。

2 监管博弈模型求解

由于企业与政府之间的博弈不存在纯策略纳什均衡，所以通过混合策略纳什均衡进行双方博弈。假设企业的混合策略U1=(安装，不安装)，政府的混合策略U2=(监管，不监管)。

E代表博弈方的收益状况，企业在混合策略组合下选择安装相应设备策略的期望收益为E1,企业选择不安装相应设备策略的期望收益为E2，则平均期望收益为E3。

E1=(W0-C+W1)q+(W0-C+W1)(1-q)

E2=(W0-M-W2)q+(W0-W2)(1-q)

E3=pE1+(1-p)E2

政府在混合策略组合下选择监管的期望收益为E4，政府选择不监管的收益期望为E5,则平均收益期望为E6。

E4=(-F0)p+(-F0+M-D)(1-p)

E5=0p+(-N)(1-p)

E6=qE4+(1-q)E5

则企业选择策略行为的动态复制方程分别为

p(1-p)(Mq+W1+W2-C)

政府选择策略行为的动态复制方程分别为

q(1-q)(-Mp+Dp-Np+M-D-F0+N)

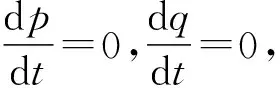
因此,可求出博弈双方的鞍点值

通过对雅可比矩阵的计算，即分别对企业和政府双方的复制动态方程p、q进行求导，可得出雅可比矩阵为

则此雅可比矩阵的行列式结果为

|J|=(1-2p)(Mq+W1+W2-C)·

(1-2q)(-Mp+Dp-Np+M-D-F0+N)-

p(1-p)M·q(1-q)(-M+D-N)

雅可比矩阵的迹为

tr(J)=(1-2p)(Mq+W1+W2-C)+

(1-2q)(-Mp+Dp-Np+M-D-F0+N)

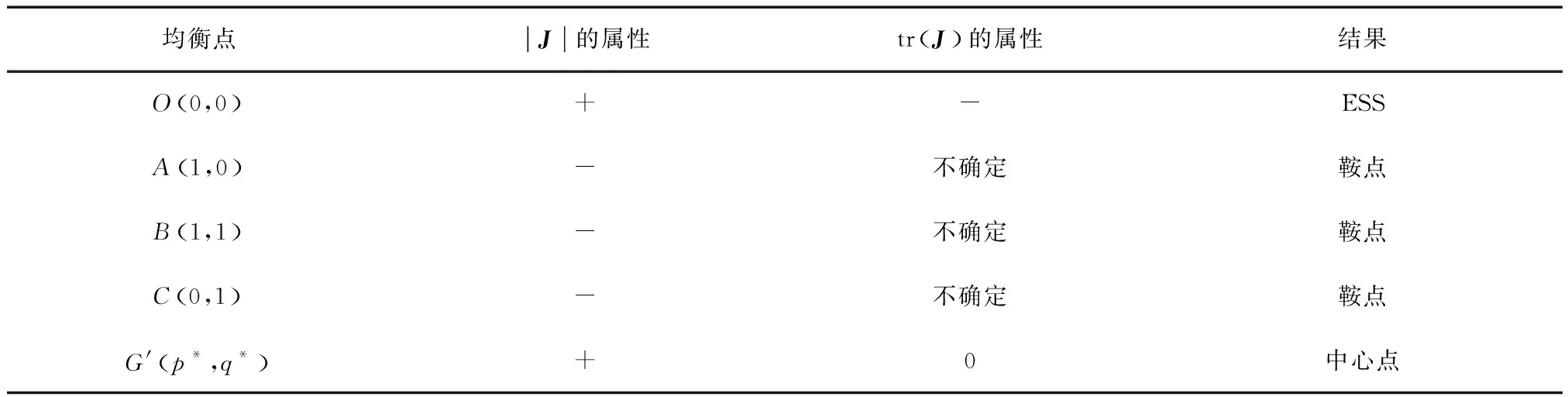
由此可得出博弈双方局部稳定结果(见表2)。

表2 博弈双方局部稳定性分析

针对离散系统，当且仅当det(Jacobi)>0,tr(Jacobi)<0时，该点为ESS(进化稳定策略)稳定点。由于博弈矩阵中相关变量相对取值不同，det(Jacobi)和tr(Jacobi)的正负可能性也会不同，企业由于安装消毒设备增加的收益是来自于其他相关企业的损失收益，以及其余出行方式转移而来的收益之和，故W1≫W2。所以，从政府和企业两个方面博弈角度出发，起决定作用的相关变量为W1和C以及F0-M与N-D的大小关系。下面将从这两组不同大小的4种组合进行相关分类讨论，进而得到不同大小组合情况下的均衡点类型。

3 演化博弈仿真

3.1 参数间大小关系说明

W0不参与双方博弈，W2对企业与政府间博弈影响可以忽略。企业安装付出的成本C与安装后给企业带来的收益W1之间的大小关系直接决定了企业是否会安装头盔消毒装置，企业监管付出总成本F0-M与企业不监管产生的社会危害N-D的大小关系决定了政府是否会监管企业进行头盔消毒装置的安装。

3.2 针对不同情况下博弈仿真

1)当W1>C且F0-M>N-D

此时，企业因安装消毒设备增加的收入大于其安装费用及后期维修管理的成本之和，政府监管产生的花费大于政府不监管产生的社会危害。

系统有4个均衡点：O(0，0)，A(1，0)，B(1，1)，C(0，1)，均衡点类型判断如表3所示。

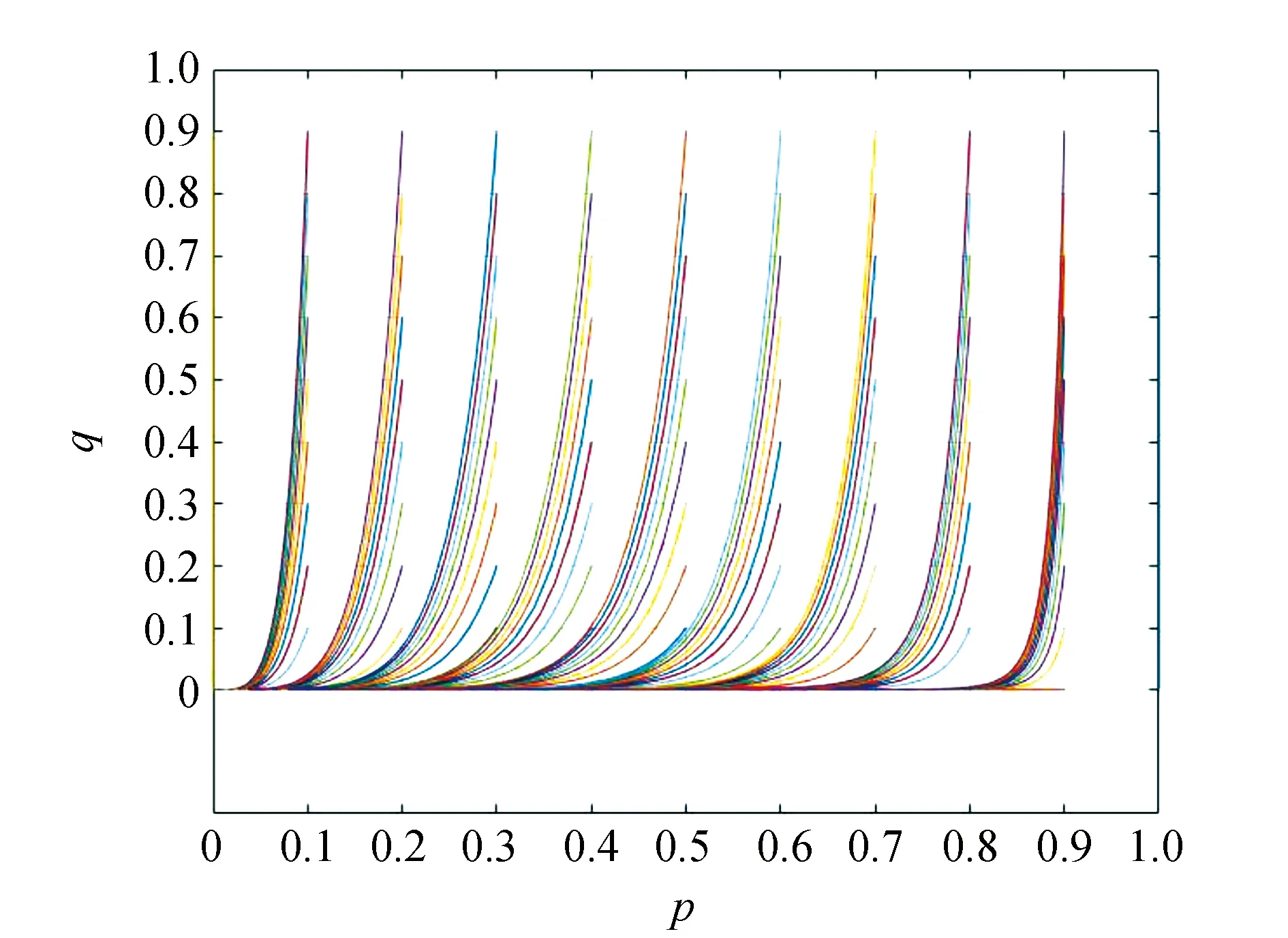
从表3可以看出系统稳定点为A(1,0)，针对当前条件W1>C且F0-M>N-D，对其进行具体取值:W1=6，C=4，N=5，D=3，F0=7，M=1，W2=1。对G(p,q)做出不同初始值下的博弈系统演化路径，如图1所示，分析其演化规律。p，q初始值分别取自向量(0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0)。

表3 W1>C且F0-M>N-D时均衡点类型判断

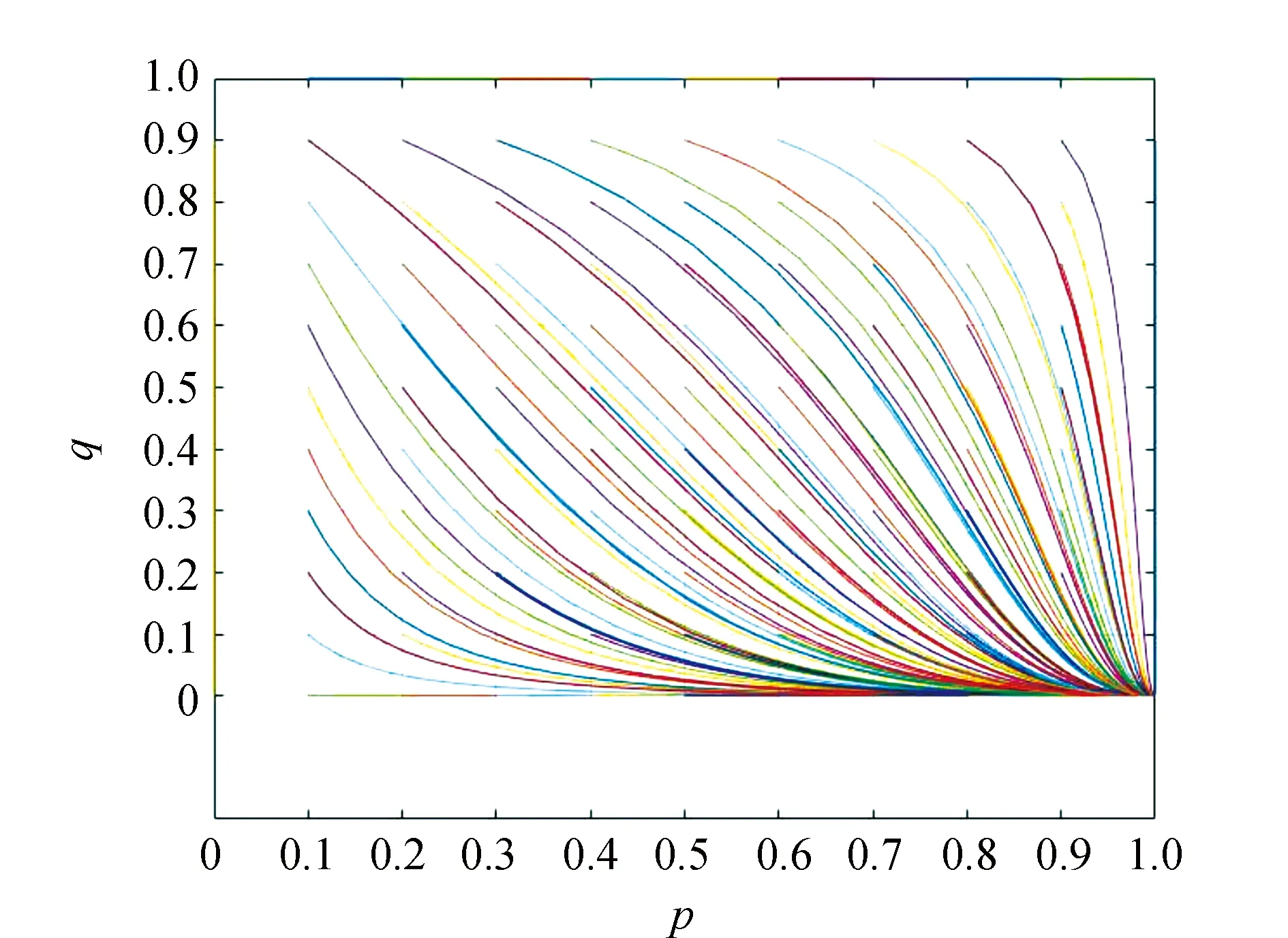
图1 W1>C且F0-M>N-D时演化路径

根据图1所示，所有给定值经过一段时间的演化后最终都收敛到A(1，0)点，可以理解为无论企业和政府的初始选择概率如何，最终都会向着企业安装、政府不监管的方向演化。在双方博弈过程中，企业所获收益大于企业安装以及后期的维修成本，最终企业安装相关设备的概率p趋于1。政府监管付出的成本大于由于监管减少的社会危害，所以最终政府监管的概率q趋于0，系统最终达到A(1，0)的状态。

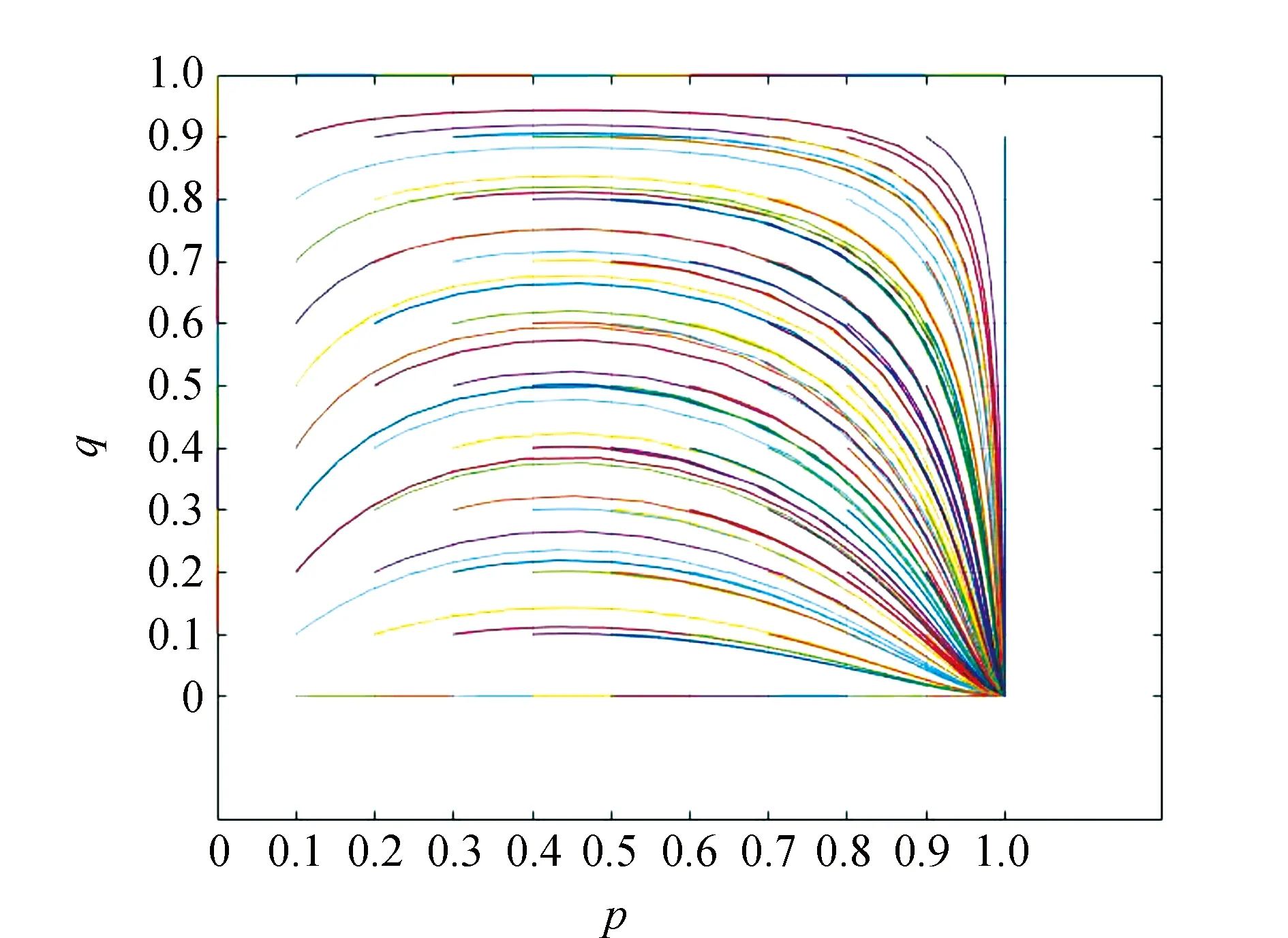
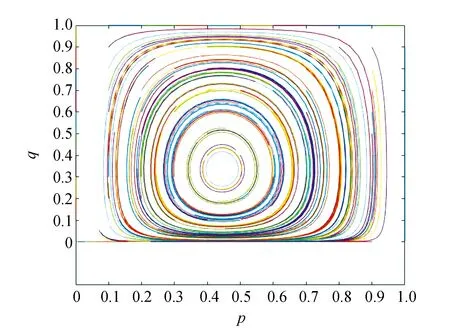
2)当W1>C且F0-M

此时，企业因安装消毒设备增加的收入大于其安装费用及后期维修管理的成本之和，政府监管产生的花费小于政府不监管产生的社会危害。

系统有4个均衡点：O(0，0)，A(1，0)，B(1，1)，C(0，1)，均衡点的类型判断如表4所示。

表4 W1>C且 F0-M

从表4可以看出系统稳定点为A(1,0)，C(0,1)为鞍值点，针对当前条件W1>C且F0-M

图2 W1>C且F0-M

如图2所示，在所有给定值经过一段时间的演化后最终都收敛到A(1，0)点，可以理解为无论企业和政府的初始选择概率如何，最终都会向着企业安装、政府不监管的方向演化。在双方博弈过程中，企业所获收益大于企业安装以及后期的维修成本，最终企业安装相关设备的概率p趋于1。而此时虽然由于监管所付出的成本小于社会危害减少的成本，虽然初始状态政府选择监管的概率q趋于1,但随着企业的安装，即便不进行监管，社会危害也会降低，最终政府选择监管的概率趋于0，系统最终达到A(1，0)的状态。

3)当W1N-D

此时，企业因安装消毒设备增加的收入大于其安装费用及后期维修管理的成本之和，政府监管产生的花费大于政府不监管产生的社会危害。

系统有4个均衡点：O(0，0)，A(1，0)，B(1，1)，C(0，1)，均衡点类型判断如表5所示。

表5 W1>C且 F0-M>N-D时均衡点类型判断

从表5可以看出系统稳定点O(0,0)，A(1,0),B(1,1),C(0,1)为鞍值点，针对当前条件W1N-D时，对其进行具体取值:W1=4，C=6，N=5，D=3，F0=7，M=1，W2=1。对G(p,q)做出不同初始值下的博弈系统演化路径，如图3所示，分析其演化规律。p，q初始值分别取自向量(0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0)。

图3 W1N-D时演化路径

由图3可知，所有给定值经过一段时间的演化后收敛于O(0，0)点，可以理解为无论企业和政府的初始选择概率如何，最终的演化结果为企业不安装、政府不监管。由于企业的安装及维修成本大于由于安装带来的收益，企业选择不安装。政府的监管成本大于因监管减少的社会危害， 最终企业安装相关设备的概率p趋于0，政府选择监管的概率q趋于0,系统最终达到O(0，0)的状态。

4)当W1

此时，企业因安装消毒设备增加的收入大于其安装费用及后期维修管理的成本之和，政府监管产生的花费小于政府不监管产生的社会危害。

系统有4个均衡点：O(0，0)，A(1，0)，B(1，1)，C(0，1)，均衡点类型判断如表6所示。

从表6可以看出系统稳定点O(0,0)，A(1,0),B(1,1),C(0,1)为鞍值点，针对当前条件W1

表6 W1

图4 W1

由图4可知，所有给定值经过一段时间的演化后没有收敛，可以理解为无论企业和政府的初始选择概率如何，双方的博弈现象会一直存在。在双方博弈过程中，企业所获收益小于企业安装以及后期的维修成本，最终企业安装相关设备的概率p趋于0。而此时由于监管付出的成本小于社会危害减少的成本，所以最终选择监管的概率q趋于1,系统无法达到稳定状态，双方一直处于博弈中。

4 结 语

对共享电动车企业是否安装头盔消毒装置和相关政府单位是否会对企业进行安装监管进行博弈演化机理研究，通过建立双方博弈的收益矩阵，得到相关的复制动态方程，对相关参数大小分析进行相应的MATLAB演化仿真分析，得出以下结果：

1)通过对上述仿真图的分析，为使演化结果朝着企业效益最大、政府效益最大方向发展 ，可定向调节参数，使得W1>C且F0-M>N-D或W1>C且F0-M

2)经过市场分析，影响企业收益的因素有较多方面，笔者的研究还存在一些缺失，想要真正落实安装头盔问题，后续还应当考虑企业与企业之间以及企业与消费者之间的博弈研究，进而提高疫情下的共享出行安全。