考虑实时数据的城市道路承载量及饱和度

常 铮,裴玉龙

(东北林业大学 交通学院，哈尔滨 150040)

随着城市机动车保有量的快速增长和居民出行强度的不断提升，城市交通拥堵日趋严重，无论是交通管理者还是研究人员都在尝试从不同角度探究缓解交通拥堵的对策和方法。城市交通拥堵的实质是道路在一定时间内的实际交通需求超过了其通行能力或承载能力，因此如何科学计算城市道路实际供给与实际需求之间的关系，已成为解决城市交通拥堵问题的首要任务。为此国外学者Akamatsu等[1]运用过饱和公式对平衡状态下道路网的容量进行了计算，Chiou[2]和Wang等[3]对交通信号控制下的路网容量进行了分析，Feng等[4]利用双层模型发现开放封闭小区可使复杂城市道路网全局承载能力显著增加。García-Palomares等[5]分析了大容量路网关键路段的脆弱性、连通性及临界性，并探究了其内在关联。Laval等[6]从动静态一体化的角度对城市道路网最大承载能力进行求解，Park等[7]分析了自动驾驶对道路通行能力的影响，Dhamaniya等[8-9]则分别对行人和车辆行驶速度对道路通行能力的影响进行了较为全面的研究。

国内学者李悦等[10]基于双层规划模型和迭代优化算法实现了对道路网容量的求解，张洪宾[11]对公交停靠站对快速路出口通行能力的影响进行了研究，杨阳等[12]介绍了利用融合浮动车数据预测城市道路通行能力的方法，邵长桥等[13]分析了路侧停车行为对城市道路通行能力的影响，安连华等[14]基于交通大数据对城市道路容量进行了标定，张雪、李婷[15-16]分别基于耗散结构理论和改进出行时耗模型对城市道路网承载力进行分析。

虽然国内外学者已针对城市道路的容量或通行能力开展了一定研究，但大多仅从交通供给角度对城市道路网或其关键路段理论最大承载能力进行计算，对城市道路实际交通需求方面的研究相对较少。此外，由于现有城市道路容量或承载量的计算方法大多依靠理论公式进行推算，或利用局部路段的小样本观测数据进行扩样，其计算过程缺乏充分且可靠的数据支持，因此,结果的科学性及准确性有待论证。笔者针对以上不足，创新性提出实际承载量概念，尝试从实际交通需求角度探究城市交通的管理方法，依托数据爬取技术实现城市道路网大范围、全覆盖的实时交通数据连续采集，克服传统路网容量或承载量计算方法中基础数据不足的缺陷。最后，基于交通流理论构建既可用于整体路网又可用于局部路段的实际承载量及饱和度计算模型，并依托全样本实时交通数据实现模型求解，极大提升计算结果的真实性和可靠性。

1 基于Python的实时交通数据爬取及预处理

传统交通调查方法受调查方法和技术条件限制，往往仅能获取城市道路局部路段或部分时段的小样本观测数据，难以在时间和空间上实现城市道路网全样本实时交通数据的连续采集。为克服此问题，研究采用基于Python的数据爬取技术，为城市道路网实时交通数据的批量获取提供新思路。

1.1 数据来源

1.1.1 实时交通数据

目前国内外众多地图导航平台均提供了实时交通查询服务，其中百度作为一个面向大众的开放地图服务平台，能够实现全球7 000万km的路网覆盖和分钟级的道路交通状况数据更新，十分适合二次开发或研究。因此文中研究选择调用百度地图Web服务API中的实时路况查询服务，对实时交通数据进行批量获取。

1.1.2 城市道路数据

OpenStreetMap(OSM)是一个全球矢量地图开源网站，其数据精度高、质量好、覆盖广且开源免费[17]，并可提供详细道路等级、交叉口类型、道路属性及表面材质等数据信息，目前已在交通及地理信息研究领域得到了广泛应用。通过OSM开源网站实现了城市道路矢量数据的获取，并以此为基础利用ArcGIS软件构建了可用于后期计算分析的城市道路模型。

1.2 基于Python的实时交通数据爬取与解析

1.2.1 Python网络爬虫原理

网络爬虫是一种按照特定规则自动抓取网络信息的程序或脚本，可在互联网的海量信息中根据指定规则对数据进行抓取、解析和存储[18]。其原理为爬虫程序从待爬取网页队列中的一个或多个初始url开始，根据指定规则过滤掉无关内容后对所需信息进行采集、保存和解析，并不断重复此操作，直至遍历队列中的所有url为止。Python作为21世纪最热门的编程语言之一，其针对网络爬虫提供了众多功能强大的扩展库，在大大简化了爬虫程序表达的同时大幅提升了爬取成功率，使大范围批量爬取地图数据成为可能[19]。

1.2.2 实时交通数据爬取与解析

百度地图提供了多种实时交通数据获取方法，其中周边区域路况查询是将城市道路切割为若干采集区域，通过发送每一个采集区域中心点的经纬度坐标至百度地图服务器来批量获取采集区域各路段的实时交通数据，其操作简单且定位精准，十分适合大范围城市道路实时交通数据的批量采集。

具体思路为使用ArcGIS软件生成采集区域坐标集，并利用Python中的pandas库对坐标集进行读取，随后使用range函数配合for循环实现对坐标集中坐标的循环提取，并将所提取的坐标与在百度开放平台申请的开发者密钥key组合，构建不同的请求url，最后利用Python中的requests库将所构建的请求url批量发送至百度地图开放平台，并通过pandas库将返回的数据进行解析及存储，完成整个爬取过程。百度地图实时交通数据爬取与解析过程如图1所示。

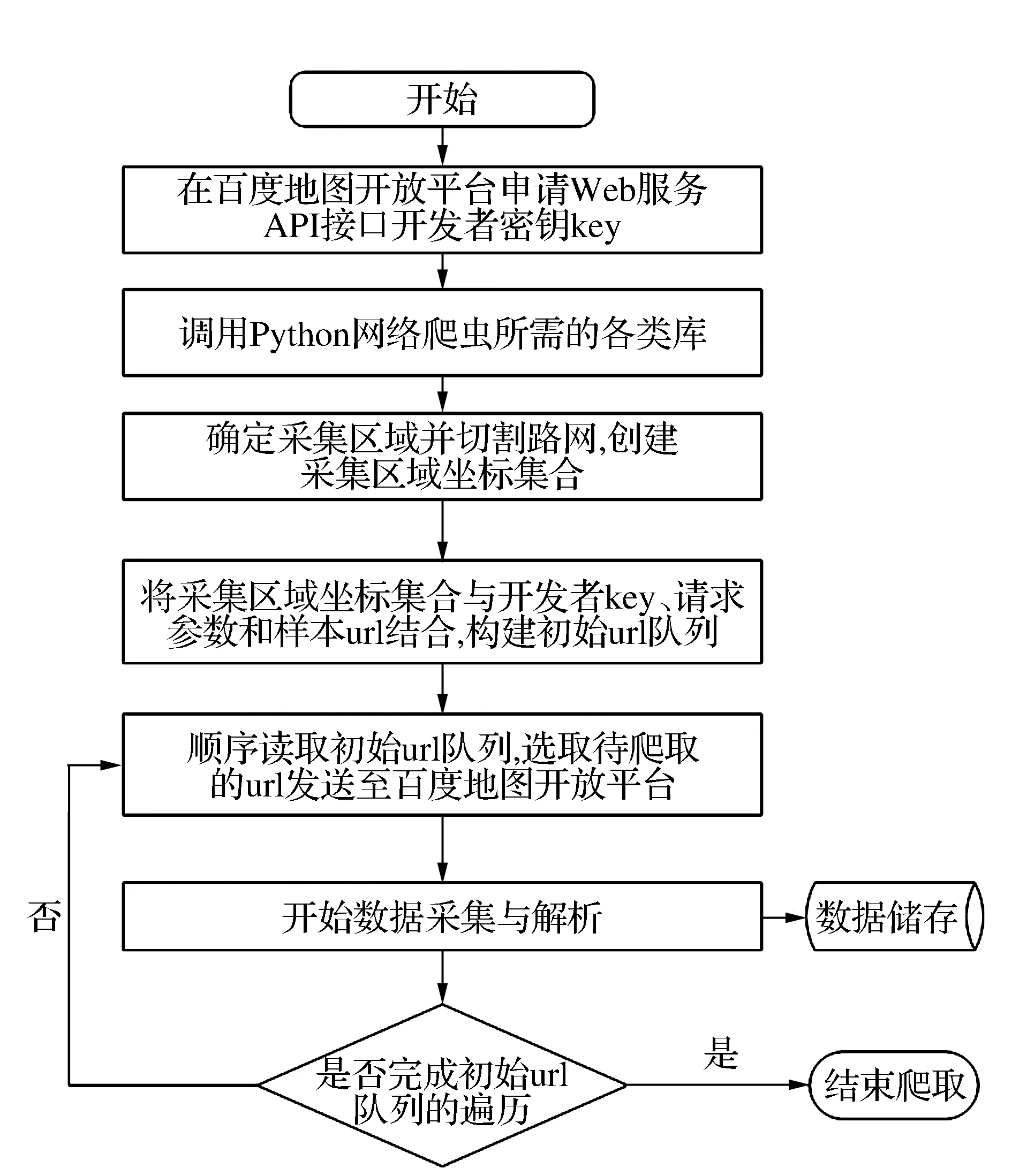
图1 百度地图实时交通数据爬取过程

1.3 实时交通数据预处理

1.3.1 数据清洗

实时交通数据爬取所返回的数据中除了包含研究所需的道路信息外，还包含一些较低等级的无关道路信息。因此需要对爬取数据进行筛选及清洗，剔除不相关的冗余信息，以免对后续计算造成不必要的影响。

1.3.2 数据修复

通过百度开放平台进行实时交通数据爬取时，只有拥堵或严重拥堵路段才能返回速度及拥堵评价数据，当道路畅通时则无法返回详细道路交通状况信息。为保证数据完整，可按照《城市道路交通规划设计规范(GB 50220-95)》中所规定各等级道路最高设计速度的70%～80%对无速度属性的路段进行填充与修复。

1.3.3 平均行程速度计算

为消除由偶然事件对城市道路各路段平均行程速度的影响，可将调查期间内各路段行程速度的平均值作为路段的平均行程速度，算式为

(1)

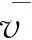
2 城市道路实际承载量模型

2.1 考虑交叉口延误的道路空间资源计算

道路空间资源即城市道路中各路段可供车辆通行的资源，一般情况下道路空间资源越大其单位时间所能承载的车辆数也越多。然而在实际情况中，由于各类因素的影响导致道路空间资源很难实现百分之百的利用，因此需要对道路实际可被利用的空间资源进行计算。其中交叉口是决定道路空间资源利用率的主要因素之一，车辆在交叉口处停车等待会在一定程度上影响道路通行能力，进而降低道路空间资源的实际利用率，因此在进行城市道路空间资源计算时必须考虑交叉口的影响。其中交叉口折减系数β可按式(2)计算[20]。

(2)

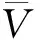
城市道路空间资源可表达为道路网中各路段长度与其机动车道总宽度乘积之和，在实际情况中，道路可利用的空间资源除会受到交叉口影响外，还会受到道路等级和车道数量等因素影响，因此,还需要对模型进一步修正，最终得到城市道路可利用空间资源模型算式为

(3)

式中：A为城市道路可利用空间资源，Ai为第i个路段可利用空间资源，li为第i个路段的长度，di为第i个路段所有机动车道的总宽度，βi为第i个路段的交叉口折减系数，μi为第i个路段的车道折减系数，αi为第i个路段的道路等级折减系数。

若某一行车方向仅有一条车道时折减系数为1.00，其余车道的折减系数如表1所示[21]，若快速路道路等级折减系数为1.00，其余等级道路折减系数如表2所示[22]。

表1 车道折减系数

表2 道路等级折减系数

2.2 基于交通流特性的道路实际承载量模型

道路实际承载量反映的是某时刻城市道路各路段实际承载的车辆数，其计算的关键在于城市道路各路段实际车流密度的获取。通过Python爬取百度地图中各路段的实际行程速度，并基于交通流3个参数中速度与密度的关系即可实现各路段车流密度的推算。通常情况下交通流3个参数中速度与密度之间一般对应3种模型，即格林希尔茨直线模型、安德伍德指数模型和格林柏对数模型，由于上述模型属于交通流理论中的经典模型，故不再对其计算方法及适用条件做过多赘述。

在获取到实际车流密度后，可利用道路有效长度与实际车流密度的乘积对其实际承载量进行计算，如式(4)所示。

(4)

式中：C为城市道路实际承载量，Ci为第i个路段的实际承载量，Ai为第i个路段的可利用空间资源，ri为车辆在第i个路段行驶时占用的横向宽度，Ki为第i个路段的实际车流密度。

根据交通流3个参数中速度与密度之间的关系，将已建立的城市道路可利用空间资源模型带入式(4)中，即可得到城市道路实际承载量的畅通模型、缓行模型和拥堵模型，如式(5)～(7)所示。

2.2.1 畅通模型

畅通模型一般适用于交通流密度较小、交通流处于自由流状态的路段，在此状态行驶中的车辆受其他道路中其他交通单元的影响较小。此时车辆平均运行速度与交通流密度符合安德伍德指数模型，算式为

(5)

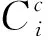
2.2.2 缓行模型

缓行模型一般适用于交通流密度适中、交通流处于正常运行或缓行状态路段，在此状态下同路段中行驶的车辆彼此之间会产生一定限制。此时车辆平均运行速度与交通流密度符合格林希尔茨直线模型，具体算式为

(6)

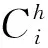
2.2.3 阻塞模型

阻塞模型一般适用于交通流密度很大、交通处于拥堵或严重拥堵状态路段，在此状态下车辆行驶速度极大受限，无法根据自身意愿行驶。此时车辆平均运行速度与交通流密度符合格林柏对数模型，算式为

(7)

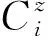
最后通过融合畅通模型、缓行模型和拥堵模型即可得到城市道路实际承载量算式(8)。基于此公式并结合前文所爬取的实时交通数据，即可实现对城市道路实际承载量时空分布特性的分析及研究。

C=Cc+Ch+Cz

(8)

式中：C为城市道路实际承载量，Cc为城市道路网中畅通路段实际承载量总和，Ch为城市道路网中缓行路段实际承载量总和，Cz为城市道路网中阻塞路段实际承载量总和。

因此，本模型既可用于计算局部路段的实际承载量，又可用于计算整体路网的实际承载量。

3 城市道路实际饱和度模型

为进一步探究城市道路各路段的实际利用情况，提出实际饱和度概念，并通过各路段实际承载量与理论容量之比对其进行计算。其中，路段的理论容量可理解为交通流处于最佳运行状态时路段所能容纳的最大车辆数，其算式为

(9)

式中：N为城市道路理论容量，Ni为第i个路段的理论容量，hi为第i个路段运行效率最大时所对应的平均车头间距，其余参数物理意义与前文相同。

其中，路段运行效率最大时所对应的平均车头间距h可按快速路为27.92 m、主干路25.56 m、次干路21.88 m及支路15.50 m进行取值[23]。

计算出城市道路各路段理论容量后，其实际饱和度可通过式(10)求得。

(10)

式中：Ei为第i个路段的实际饱和度，Ci为第i个路段的实际承载量，Ni为第i个路段的理论容量。

通过模型可以看出，在理论容量一定时路段实际饱和度主要由其实际承载量决定，当路段实际饱和度大于1时，代表其实际承载的车辆数超过了理论容量，此时虽然路段的资源利用率较高，但车辆密度的增大会使路段中产生较为严重的拥堵，从而影响道路的整体运行效率。反之，若路段实际饱和度过低，则表明路段中实际承载车辆数过少，道路资源存在一定冗余，同样不利于道路整体运行效率的提升。

4 案例分析

4.1 数据爬取及处理

阿城区地处哈尔滨市中心城区东南23 km处，是黑龙江省最具经济活力的区(县)之一，对其城市道路实际承载量及饱和度进行分析具有十分重要的意义。通过Open Street Map(OSM)网站获取阿城区城市道路，其中包含快速路2条、主干路7条、次干路12条、支路15条，总长度约59.68 km。运用ArcGIS软件中的渔网工具将城市道路按不同等级分割为若干采集区域，并利用自编Python爬虫程序对采集区域道路的实时交通数据进行爬取，爬取时间为07：00—18：00，间隔30 min，调查期间共采集7天 161个时刻的实时交通数据。将实时交通数据根据前文所述方法进行清洗、筛选及修复处理后，按照经纬度坐标及道路名称等属性将其链接进城市道路模型中，用于后续的计算与分析。阿城区道路模型如图2所示，按文中1.3节所述方法处理计算后的高峰时刻实时交通数据(见表3)。

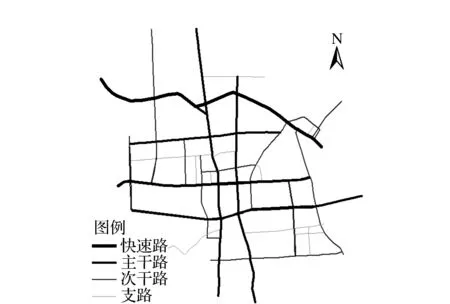
图2 哈尔滨市阿城区道路模型

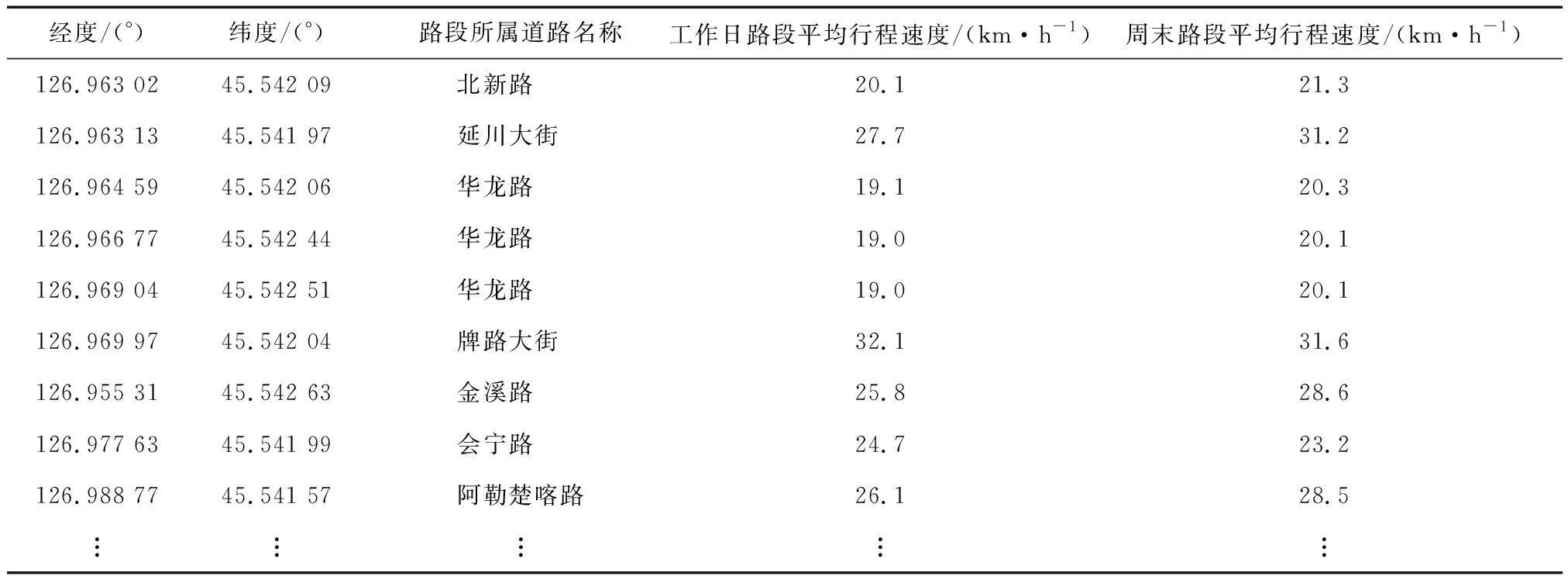
表3 处理后高峰时刻实时交通数据

4.2 实际承载量及其时空特性分析

4.2.1 时间特性

通常情况下城市道路工作日和周末的交通流会呈现较大的差异性，分别对阿城区工作日和周末城市道路不同时刻的实际承载量进行计算，并绘制其时间特性曲线(见图3)。根据曲线可对阿城区城市道路实际承载量的时变特性做出以下分析。

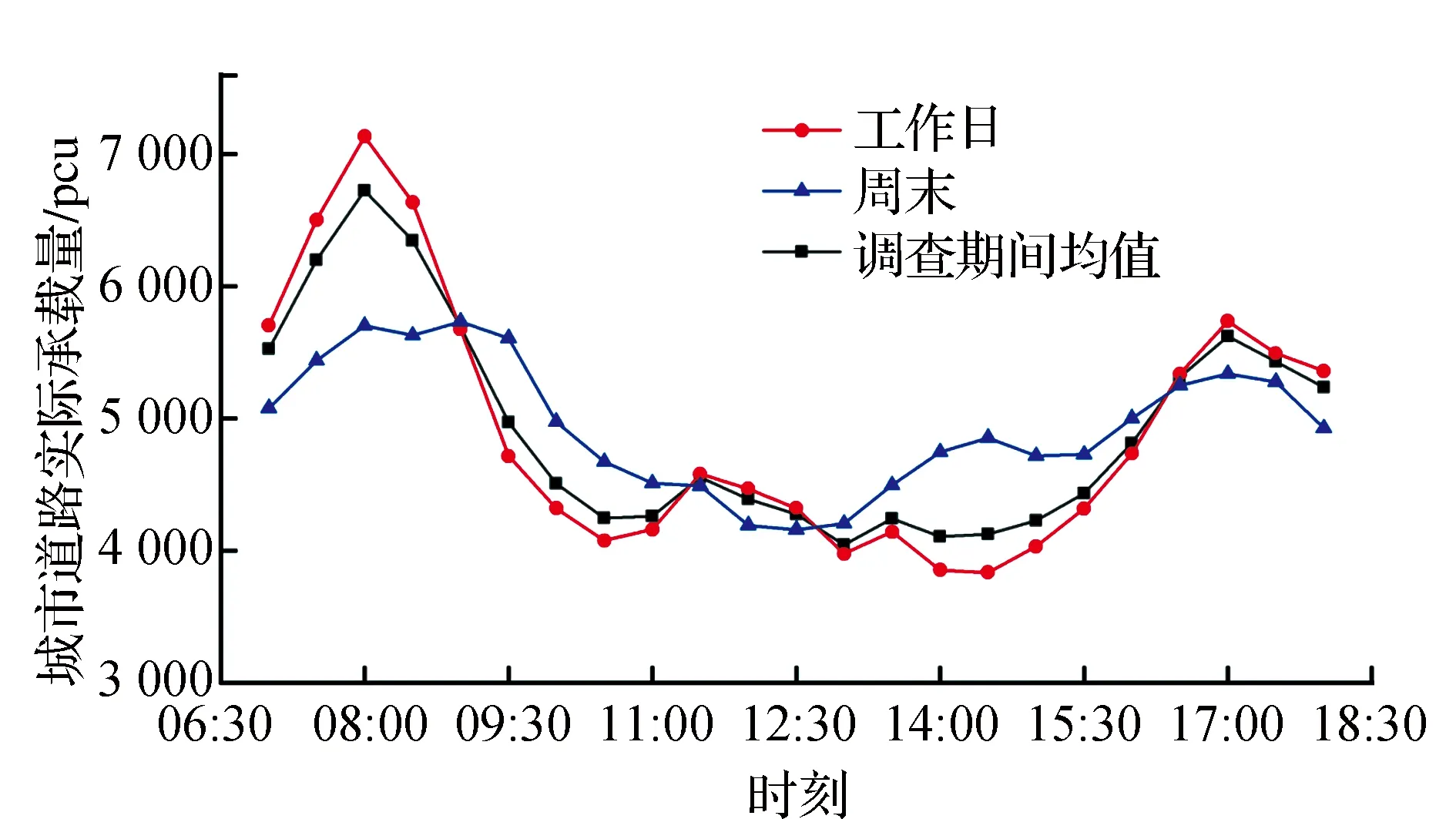
图3 城市道路实际承载量时间特性曲线

1)阿城区城市道路实际承载量在早晚高峰(即07：30—08：30和16：30—18：00)存在明显峰值，表明工作日早晚高峰时段城市道路中所承载的车辆总数最多；而周末实际承载量曲线无明显峰值，说明周末居民出行的集中性较弱。

2)在曲线波动性方面，阿城区工作日城市道路实际承载量的波动性明显强于周末，其曲线整体呈马鞍型，平峰时段(即09：30—15：30)城市道路实际承载量仅为高峰时段的60%左右。而周末虽然高峰时段城市道路实际承载量低于工作日，但在平峰时段却高于工作日。

3)通过对一周内不同时刻城市道路实际承载量进行分析可以发现，工作日城市道路实际承载量与时间之间具有较为明显的关联性，因此，交通管理者可以根据实际承载量的时间特性提出差异化的管控措施，提升城市道路的整体运行效率，进而实现从交通需求角度缓解交通拥堵。

4.2.2 空间特性

由城市道路实际承载量的时间特性分析可知，阿城区早高峰城市道路的实际承载车辆总数约为7 133 pcu，而其他时刻均低于该值，表明阿城区早高峰居民出行强度最高，因此，对早高峰实际承载量的空间特性进行分析具有重要意义。采用ArcGIS线密度分析方法，以实际承载量作为权重字段生成栅格分析(见图4)。可以看出工作日和周末各路段实际承载量在空间分布上均呈现由中心向边缘递减的趋势，其中工作日高峰时刻出行热点主要聚集在解放大街与延川大街交叉口附近；而周末高峰时刻出行热点主要聚集在解放大街与会宁路交叉口附近，城区西南部长安路附近也有一定量的交通聚集。

4.3 实际饱和度分析

分别对阿城区工作日早高峰不同等级路段理论容量和实际承载量进行计算，并将二者之间的关系表达为如图5所示。

1)高峰时刻快速路和主干路的实际承载量与理论容量之间相关性较强，而次干路和支路高峰时刻理论容量与实际承载量之间并无明显线性关系。此现象主要原因是快速路和主干路整体服务水平较高且道路内车流连续，速度波动小，而次干路与支路由于长度较短且宽度较窄，易受交叉口及路侧非机动车干扰，导致路段实际承载量的波动较大。

2)根据拟合曲线可以看出，虽然快速路与主干路实际承载量与理论容量总体上呈正相关，但随着路段理论容量的增大，实际承载量的增长速度会逐渐降低。这是由于通常情况下区域交通需求是固定的，当道路总供给大于实际交通需求时，道路的实际承载量将不会再继续提升，此时若继续提升道路容量则会出现资源冗余现象。

3)在理论容量相同的情况下，快速路或主干路高峰时刻的实际承载量明显大于次干路和支路，主要是由于在路段理论容量相同的情况下，快速路或主干路往往拥有更丰富的空间资源以及更高的服务水平，出行者更倾向于选择高等级道路通行，因此，高等级道路路段的实际承载量更高。

为探究不同等级道路的实际饱和度差异，对阿城区不同等级道路的实际饱和度进行计算，结果如图6所示。可以看出在高峰时刻主干路实际饱和度均值接近1.0，快速路实际饱和度均值约为0.7，而支路和次干路实际饱和度均值仅为0.5左右。表明高峰时刻不同等级道路空间资源利用情况差异较大，其中主干路空间资源利用率最高，其高峰时刻实际承载量均值已经接近理论容量，部分路段甚至已超过理论容量，处于超负荷运行状态；而次干路和支路实际饱和度普遍较低，因此在进行交通管理时应着重加强交通量由高等级道路向低等级道路的疏导，在提升城市道路整体资源利用率的同时避免高等级道路出现拥堵。

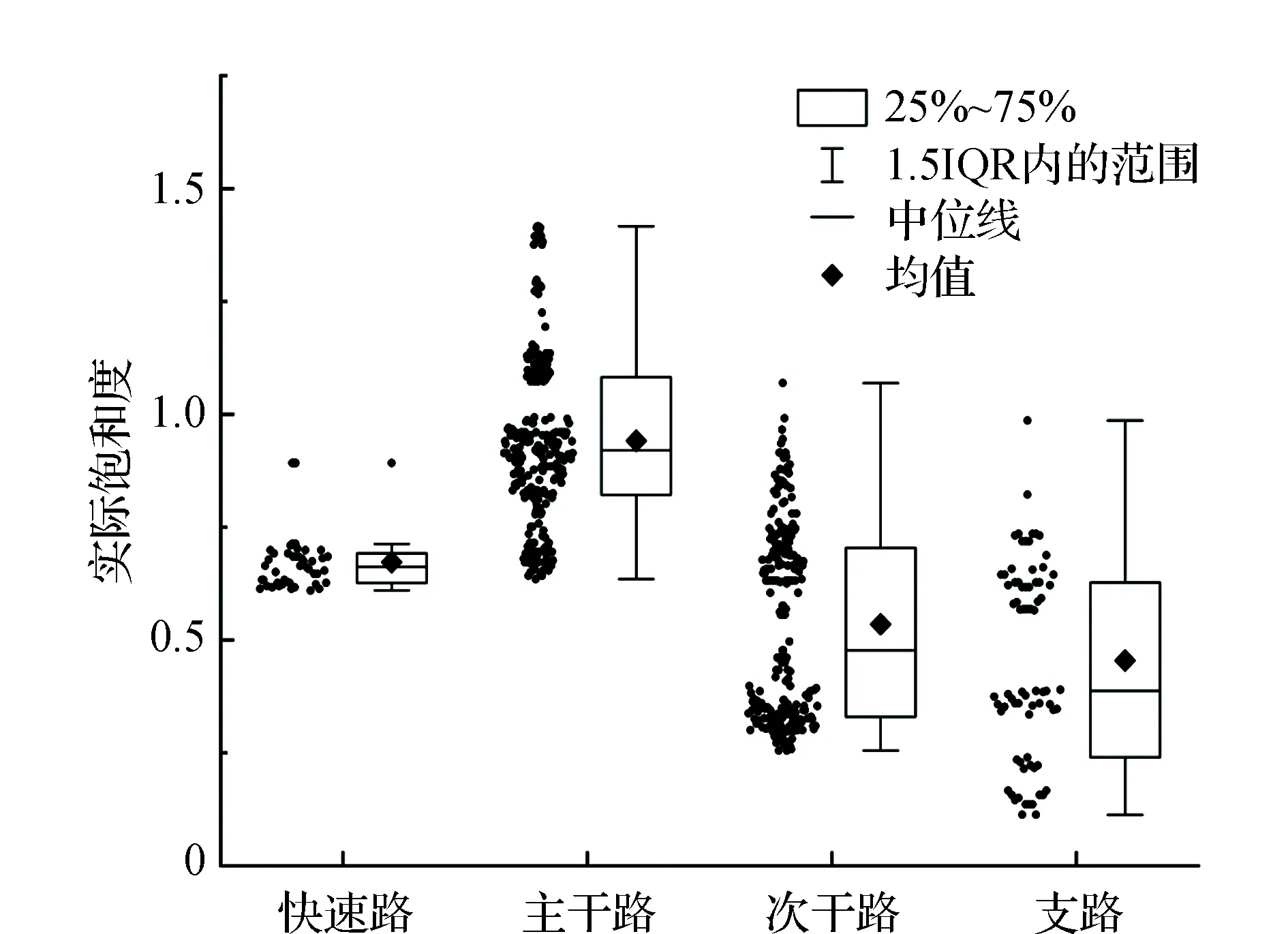
图6 不同等级道路实际饱和度

5 结 论

从实际交通需求出发，通过一种新的视角探索缓解城市交通拥堵的对策和方法，利用网络爬虫技术实现了城市道路全样本实时交通数据的连续采集，并提出了基于实时交通数据的城市道路实际承载量及饱和度计算方法。相比于传统道路交通量测算方法，该方法思路清晰、简单实用且效率更高，此外得益于可获取大范围、全样本实时交通数据的数据爬取技术，该方法理论上可用于任意规模的城市道路网或局部路段实际承载量的推算，具有较强的普适性和先进性。通过对阿城区城市道路实际承载量及饱和度进行分析，可得出以下结论。

1)高峰时刻快速路和主干路的实际承载量与理论容量之间的相关性较强，而次干路或支路高峰时刻实际承载量与理论容量之间相关性较弱，因此，可推测快速路和主干路通行能力或承载能力的改变对高峰时刻城市道路整体承载量的影响更为明显。

2)工作日高峰时刻城市道路实际承载量最高，且主要集中于城市中心区域，其余时刻城市道路实际承载量仅为高峰时刻的60%左右。这表明工作日居民出行在时间和空间上较为集中，而周末不同时段城市道路实际承载量相差不大。因此，可针对实际承载量的时空分布特性为不同道路制定差异化的管理措施，提升城市道路的整体运行效率，进而缓解交通拥堵。

3)从整体上看，快速路与主干路高峰时刻实际饱和度高于次干路与支路，这说明在高峰时刻出行者更倾向选择高等级道路出行。考虑未来汽车保有量的增长以及居民出行强度的提升，为避免高峰时刻快速路或主干路出现交通拥堵，在进行交通管理时应注意将交通量由高等级道路向低等级道路进行疏导。