基于混频数据模型实时预测效果分析——以中国GDP增速为例

许飞

安徽大学，安徽 230031

一、引言

一直以来，宏观经济预测对于政府制定决策以及相关部门采取相应措施至关重要，如2021年“两会”提出欲完成年度国内生产总值6%以上的目标，基于此，进行有依据的预测和及时出台相关政策必不可少。传统的时间序列计量模型基本采用同频数据进行分析预测，而目前所能收集到的宏观经济数据以及经济指标时间序列数据多是处于不同频率，因此在建模之前需要对数据进行同频处理，即将高频数据转化为低频数据（如采用加总法、插值法）但高频数据往往能捕捉到更全面、完善的信息，亦对模型的预测结果大有改善，因此同频化会造成数据信息的损失，带来降低预测的精度甚至模型参数失效等问题。另外，由于指标数据的滞后，常常导致样本末期数据的缺失，也就是所谓的“不规则边缘”问题。如何深度挖掘更多不同频率数据间的信息，成为众多学者研究的方向。

混频数据模型的优势在于不损失高频变量数据信息的前提下，即利用原始数据信息进行建模。目前国内流行使用的方法是Ghysels等人（2004）提出的MIDAS模型，它的提出很大程度上解决了不同频率预测时所出现的信息利用不足，处理办法不统一等问题。最初的MIDAS模型用于金融市场波动性的研究，后经 Clements&Galvao（2008）证实在宏观经济变量的分析与预测的应用上有良好的效果。通过对选取指标的改进以及对方法拟合效果的研究，MIDAS模型得到越来越广泛的应用。如Andrius（2015）利用实时数据集对商品市场展开预测；Galbraith等人（2018）利用电子支付数据发现支付系统数据可以降低GDP和零售增长的预测误差。国内学者根据此模型的研究在预测中国宏观经济变量上有良好的效果。如：我国学者刘汉、刘金全（2011）将影响我国经济因素的三架马车：消费、投资和出口引入到模型中，得到不同指标解释能力和作用方式不同的结论。郑挺国（2013）将金融变量作为预测因子，建立实时数据分析数据修正给模型预测精度带来的负面影响；张伟等人（2020）构建高频舆情指数，对GDP增长率具有有效的解释能力。另外，由于高频被解释变量采样频率更高，模型中加入的滞后项容易导致参数的过度化。权重函数的选择至关重要，Ghysels（2007）给出四种权重多项式函数，其中，由于指数Almon权重函数相对较为灵活，参数较少，得到不同权重函数等优良性质被普遍使用。而 Foroni，Marcellino（2011）等人提出无约束的MIDAS模型，即不考虑模型中滞后项参数的限制，而是采用最小二乘法直接进行回归，被证实在一定条件和有约束的MIDAS模型中具有互补作用。

混频数据模型打破了传统同频计量模型的缺陷，使同时处理不同频率数据成为可能。随着越来越多研究证实基于MIDAS模型的预测效果的可靠性，更多变量被应用于模型的构建。而不同变量指标对于模型的预测能力有所差别，伴随着宏观经济数据获取的便捷和保存完整，其相关指标更加繁多，模型的预测能力和效果亦有所差别，通过单个指标进行预测的说服力和解释能力下降，指标的选取也成为影响模型的主观因素。相对而言，因子模型旨在利用少数因子代表原始变量大多数信息，能够从众多相关指标中萃取有用的信息，在经典的MIDAS模型中加入因子后有利于改善单个变量的预测能力。本文结合前期学者的研究，以先行指标、同步指标和滞后指标三个方面为基础，选取不同月度指标作为预测变量，利用混频数据模型对指标的预测精度展开探究，并从中提取公共因子代表上述指标信息，弥补单一指标预测的缺陷。同时对经典的带有参数限制的MIDAS模型与无约束U-MIDAS模型进行比较，得到在预测步长较短的情况下，无约束U-MIDAS模型预测效果更好。

二、模型构建

（一）混频数据模型（Mixed Data Sampling，MIDAS）

1.单变量MIDAS（m，k）模型

基础的MIDAS模型由Ghysels等（2004）提出，将高频变量和低频变量以参数化多项式整合在一个方程模型里，充分利用了高频解释变量中的信息，使预测结果更加准确，同时通过分布滞后多项式建模，使得模型参数大大减少。

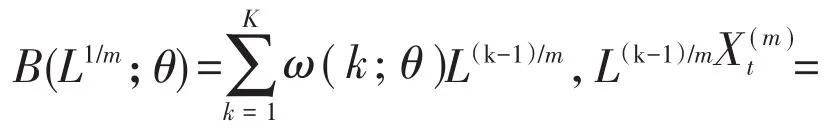
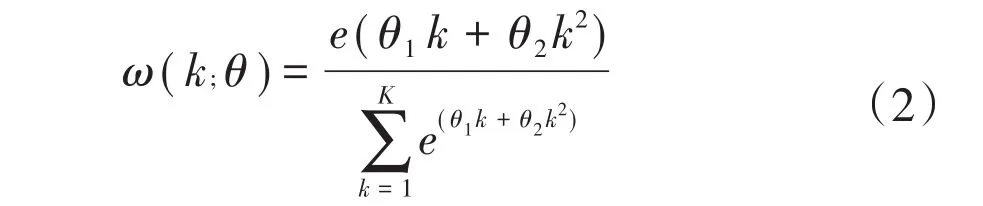
2.向前 h步预测的 MIDAS（m，k，h）模型

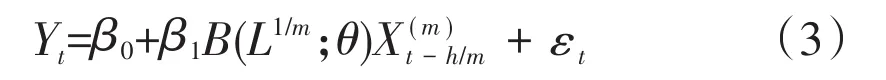
简单的MIDAS（m，k）模型只能进行样本内预测，而MIDAS（m，k，h）模型弥补了这一不足。通常情况下，高频数据收集截止时间要先于低频数据，由于高频数据的公布时间相对较早，也为实时预测提供数据基础。同时季度GDP数据的公布有一定的滞后期（以我国为例，GDP季度增长率初步核算数据在下季度首月中旬左右公布，即约40天的滞后期）无法及时对宏观经济状况进行反应，MIDAS（m，k，h）模型可以有效地对季度数据进行实时预测和修正。

3.加入自回归项的MIDAS（m，k，h）-AR（p）模型

基于经济系统往往存在惯性的原因，对宏观经济变量预测时，需要考虑自相关因素存在，如用一些月度指标来预测实际GDP增长率时，解释变量中往往会自相关，因此，在模型中加入自回归项更加符合逻辑，见模型（4）。

考虑到直接往模型中加入自回归项可能会导致季节反应，将Yt中自回归动态结构（1-λLp）作为共同因子加入模型中用来消除季节反应。

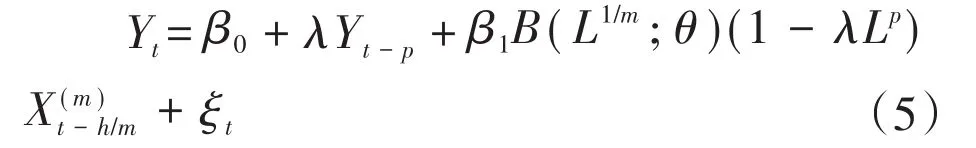
4.非限制混频数据模型（U-MIDAS模型）

经典的MIDAS模型在模型被估计之前需要对滞后权重多项式进行参数限定，以防止“维度灾难”，而在某些情况下，对权重多项式的处理过于主观，结果产生偏误。Foroni，Marcellino（2011）等人对 MIDAS 提出改进，即取消模型中对滞后权重多项式的限定，称为非限定MIDAS模型，即U-MIDAS模型。

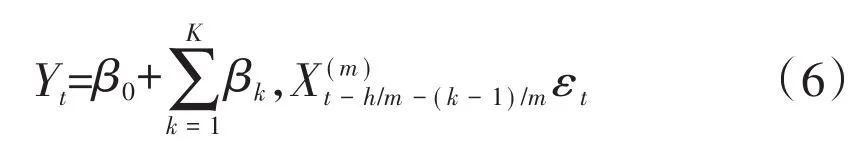
其中，最高滞后阶数为K+h-1，无约束的MIDAS模型常常需要在低频变量与高频变量之间倍差较小时使用，即上式中的m较小，如月度指标构建季度指标的模型。而本文基于月度数据选取指标，对季度GDP的实时预报和短期预测，故将两种方法放在一起比较。

（二）结合因子模型的混频数据预测模型

以上模型是基于单个指标建立的模型，对于宏观经济预测指标集常常是庞大的，将大量指标一一进行分析过于繁琐，本文结合Bai等人的研究，结合因子模型改进模型的预测效果。设Xi，t为N个选取指标中第i个月度指标同比增长率，则可以假设月度指标Xi，t可由所有指标共有的少数几个公共因子和每个指标独有的不可观测异质成分构成。即Xt，ΛFt+et则由式（7）进行预测：

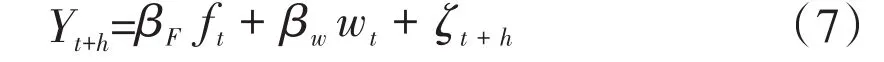
其中，Λ是有r个因子变量r×1的因子载荷矩阵，每个变量由共同成分即因子变量Ft的线性组合和随机扰动项et组成。wt为可观测变量，如Yt的滞后项，建立好因子模型后，便可利用模型进行预测，其中Ft随着TX-TY（时间差）进行更新，以获得参数估计值进行实时预测，预测模型可转变为模型（8）：

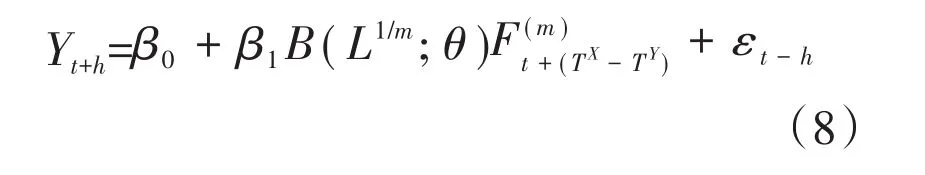
三、实证研究

（一）变量选取和数据处理

本文结合中国经济景气监测中心构建指数时选取的指标序列和郑挺国、王霞（2010）的研究成果，并兼顾数据的可获得性，基于先行指标、一致指标、滞后指标三个方面构建与季度GDP相关的18个经济指标（如表1所示），测试这些指标基于MIDAS模型预测的有效性，同时与从众多指标中提取不可观测因子建立的模型结果进行比较，从而检验萃取出的因子是否有助于提高模型预测精度。考虑到因子模型的需要，尽可能减少数据中的缺失值，本文选取从2004年1月至2020年12月的各指标月度数据作为自变量，2004年第一季度至2020年第四季度的季度GDP同比增长率作为被解释变量（其中，将2004年第一季度至2017年第四季度作为训练样本，2018年第一季度至2020年第四季度作为测试集）；另外，关于各指标含有缺失值的情况，主要采用以下方式：对于某些指标，如固定资产投资完成额、工业企业利润总额，缺失一月份数据，采用前两个月份的平均值作为代替；同时缺失一二月份数据，可利用全年年度加总值减去其他月份，再求其同比变化率；对于个别缺失数据，采用插补法进行补全。本文对各月度时间序列数据提取因子，进行降维处理；为了防止伪回归带来的影响，对萃取出的因子进行平稳性检验，并通过差分将其转化为平稳序列；最后，考虑到因子分析的需要，对平稳化序列进行标准化处理（本文数据来自中经网统计数据库和国家统计局）。另外，本文使用预测的均方误差根（RMSE）来衡量模型的预测精度，计算公式为：

表1 数据指标统计表

先行指标可以揭示未来经济的趋势，我国先行指标的峰谷平均领先一致指标6-7个月，对于经济发展的方向和转折具有重要意义，耿鹏、齐红倩（2012）验证了先行景气指标的有效性。当然，由于指标规模和数据口径、时间跨度等问题，对先行指标的选取也各有不同。本文根据中国经济景气监测系统先行指标的构成，以及数据的可获得性，选取6个指标作为先行指标序列。一致指标，又称同步指标，其波动趋势及转折点大致与国民经济的趋势及转折点相同，有利于判断当前经济的基本走势以及预测未来经济的发展走向。我国学者更青睐选取一致指标作为预测因子，如郑挺国、王霞（2012）等，本文选取9个指标作为一致指标的代表。滞后指标，时间上落后于经济周期波动，可以检验当前经济的变动情况。本文旨在检验该类指标相比较其他两类指标的预测能力，选取3个指标作为预测季度GDP的滞后指标。

（二）单变量MIDAS模型预测

单变量模型的预测，一方面希望利用可利用数据的信息量愈多愈好，即滞后阶数越长，信息量越多；另一方面，滞后阶数的增加将带来参数指数倍增加的烦恼。MIDAS的优势在于既能赋予每个高频观测值不同的权重，又能保证参数数量大幅度减少，即保留时间信息的基础上使模型变得更加灵活。结合刘汉、刘金全（2011）的方法，首先确定不同解释变量对于季度GDP预测的最优滞后阶数，在给定K值等于 3，6，9，12，15，18（Clements和 Galvao指出月度指标滞后阶数最好为3的倍数，且最大滞后阶数不超过两年，以便和基础模型进行比较），利用模型（1）对我国2018年第一季度至2020年第四季度GDP进行预测，并计算出RMSE值，如表2所示。

从表2中可以看出，不同指标对于季度GDP的解释能力不同，如税收收入的预测效果优于其他指标。而普遍使用的固定资产投资完成额，社会消费品零售总额以及进出口总额，预测精度并不突出，由此可见，仅凭单个指标作为宏观经济的预测指标说服力不足。整体上看，本次预测效果相比较以往学者预测结果，误差更大。主要原因在于2020年前期受新冠疫情的影响，包含在测试样本中的各指标以及GDP增长率陡然下降，之后又恢复正常，给模型预测精度带来一定的影响。另外，总体来说，先行指标和一致指标的预测效果更优，滞后变量组的三个指标在预测效果上并不显著。MIDAS模型主要基于当下或过去不同滞后阶数时期进行预测，而滞后指标的波动和反应趋势一般慢于一致指标，因此在预测上有效性显得不足。

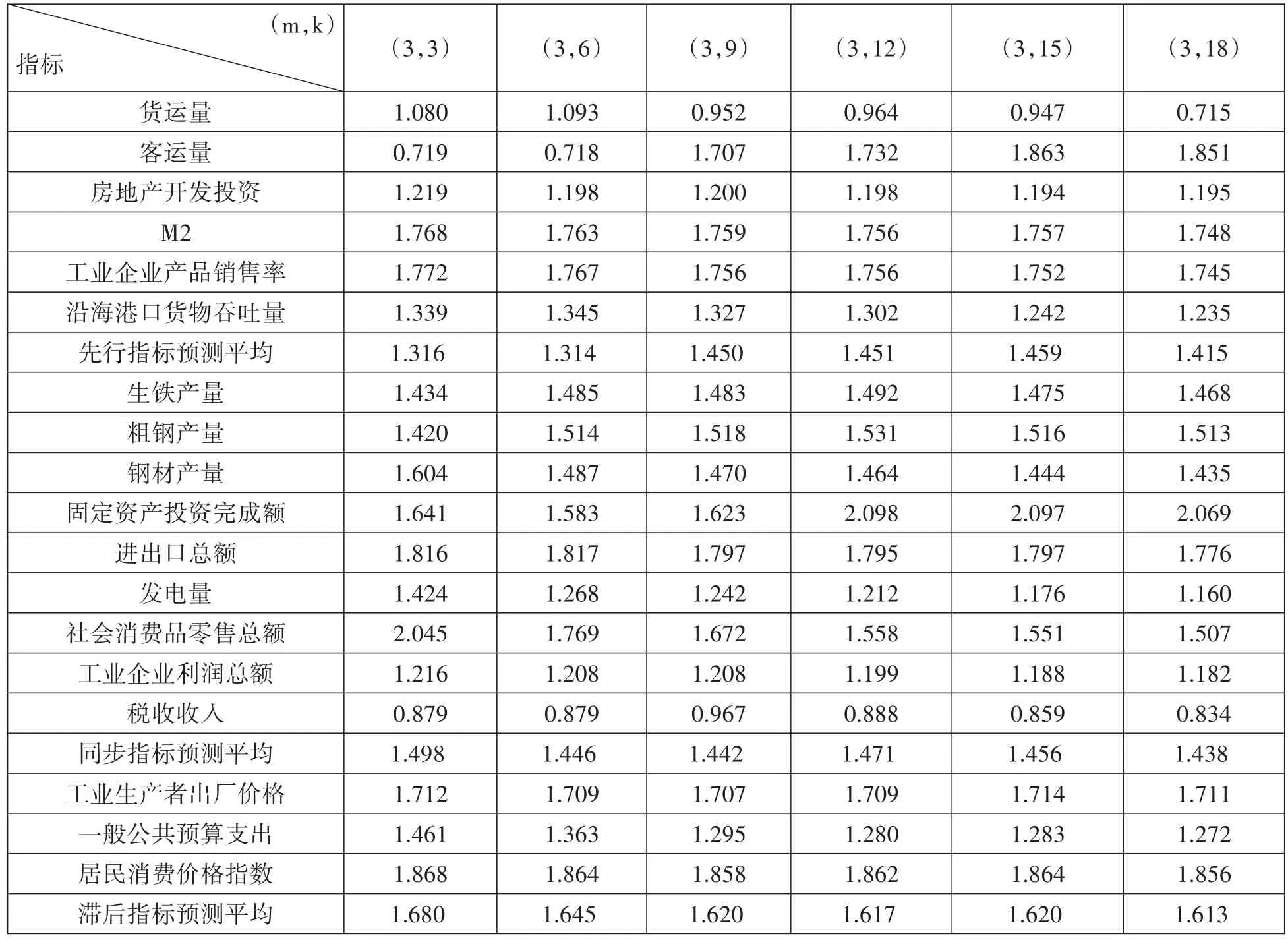
表2 单一变量在不同滞后阶数下的预测误差

随着计量模型的发展以及大量宏观经济数据获取和保存技术的提升，宏观经济总量的预测向如何使用大量具有代表性指标，尽可能利用收集到数据的有用信息发展。面对大量的高频变量数据，逐一采用计量模型进行预测，工作繁琐，且由于数据口径、时间跨度等问题，很难保证某个变量始终为预测模型的最佳变量。通常使用组合预测的方法，将所有变量的预测结果以不同的权重进行综合以提高模型的拟合效果和预测精度。Stock、Waston（2002）提出从大量变量中萃取子集，利用几个不可观测因子达到模型应用的简便性，同时也能利用所有变量中的有效信息。本文结合Stock等人的方法，利用主成分分析方法获取因子变量，具体步骤为：首先计算样本相关系数矩阵，并求其特征值，选择r个最大特征值计算对应的N×r特征向量矩阵V，利用主成分分析方法得到因子变量和因子载荷 矩 阵,其 中 ，X=（X1，…，XN），Λ =(Λ1,…,ΛN)T。

从表3可以看出，前两个因子的累计贡献率已经超过85%，能解释原始变量绝大多数信息，因此，本文将因子个数确定为2。同时，由于提取因子的方式是按特征根大小次序进行选取，两个因子的方差贡献率有所差别，因子1达到65.6195%，因此，因子1序列包含更多原始变量信息。正因为如此，因子1在后期的预测能力上相对于因子2具有更大优势。为了使因子更具有代表性意义，对提取的因子进行旋转，旋转后因子载荷结果如表4所示，发现代表供给的工业产品产量即生铁、粗钢钢材产量以及发电量在因子1上有较高的载荷，因此，因子1可视为供给因子；而房地产开发投资、工业企业利润总额在因子2上载荷最大，可视为需求因子。为了更清楚地展现两个因子与季度GDP序列的趋势和转折点，将季度GDP序列进行标准化，与因子序列趋势图进行比较，结果如图1所示。

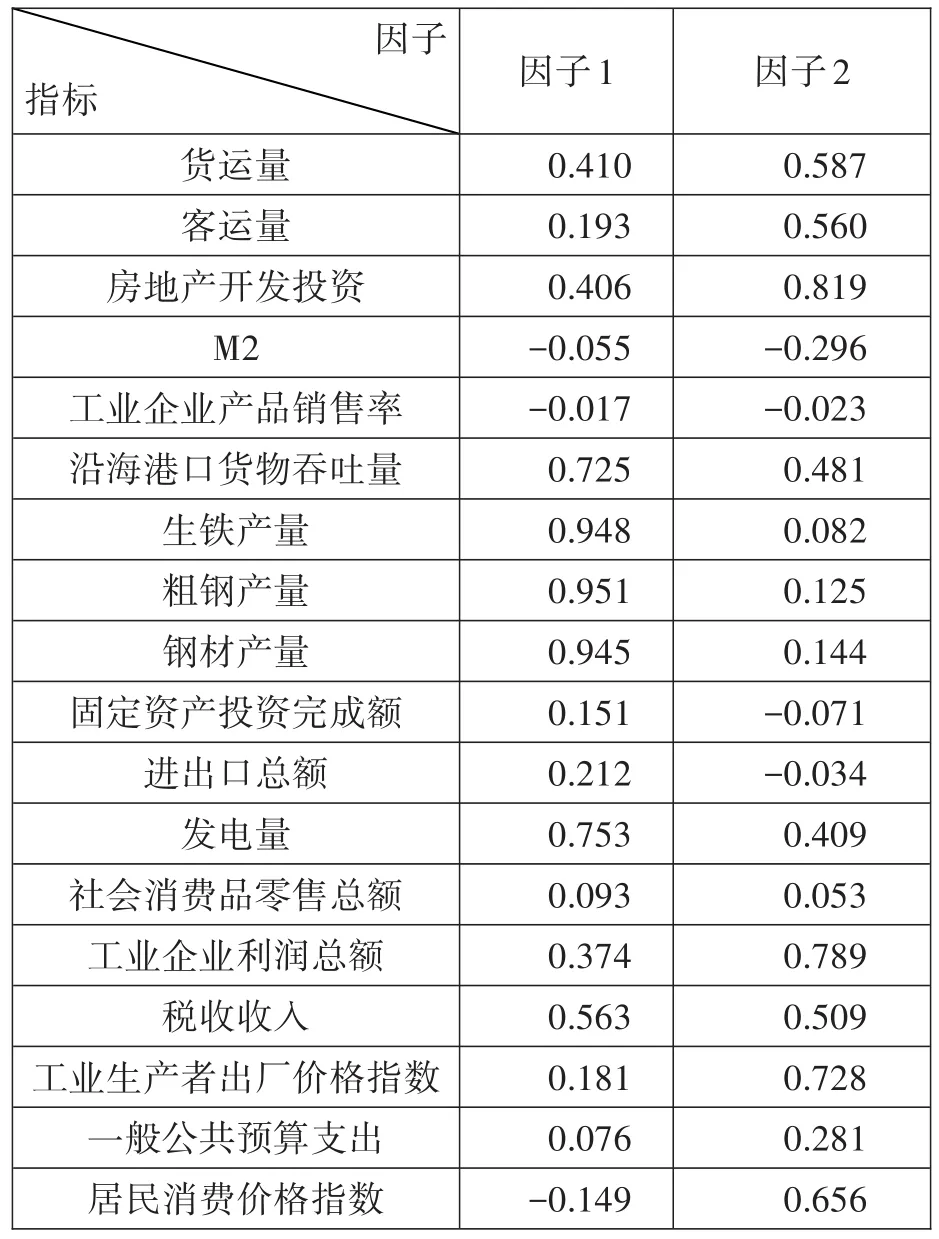
表4 旋转后因子载荷

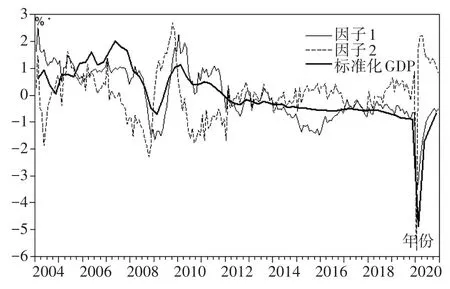
图1 因子和标准化GDP序列变化率

整体上看，因子1序列的波动趋势更接近于GDP时间序列。其中，下滑转折处集中在2005、2008以及2020年左右，分别由于房地产销售滞后、金融危机导致的进出口增长率下降和新冠疫情导致的2020年首月各指标增长率猛然跌落造成。而因子2虽然在波峰和谷底处与季度GDP序列保持形同的趋势，但整体波动性较大。

考虑到受参数限制MIDAS模型的主观性，本文结合无约束限制的MIDAS进行对比分析。从表5可以看到，基于不同滞后阶数的条件下，两种模型的预测能力各有所长。仔细观察可以看出，U-MIDAS模型在滞后阶数较短的情况下，其预测精度要优于受参数限制的MIDAS模型，而当滞后阶数增加，如：因子1变量滞后阶数达到15，18后，因子2滞后阶数超过9阶后，U-MIDAS相对来说，精度幅度下降，预测能力反而不及经典的MIDAS回归。这主要是由于U-MIDAS模型取消参数限制的影响，即避免主观上带来信息的失真，而随着滞后阶数的增加，模型参数随之增多，非限制MIDAS显得缺乏稳健性，导致模型预测结果下降，均方根误差上升。

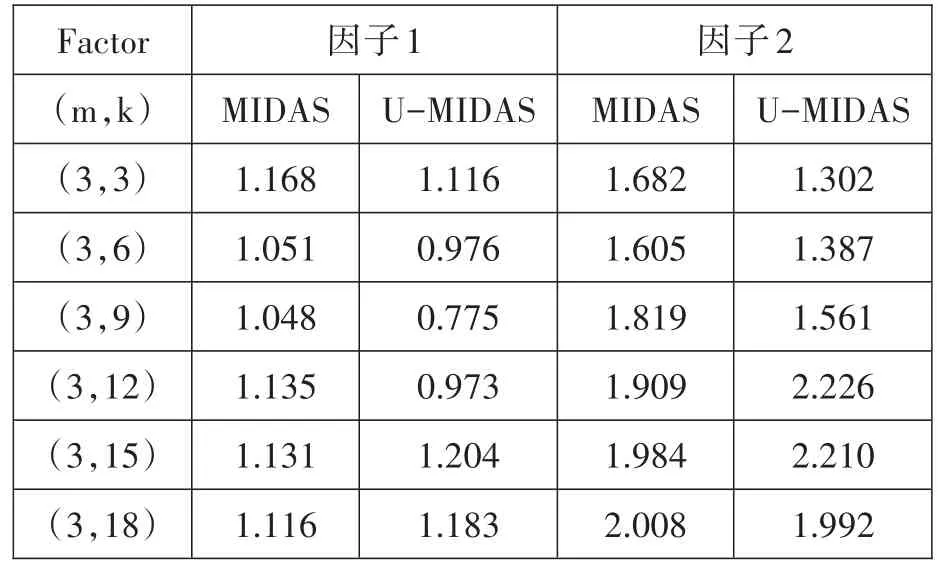
表5 因子变量在不同滞后阶数下的预测误差

（三）h步向前预测的MIDAS（3，k，h）模型

在确定完最优滞后阶数的情况下，加入h步向前预测的模型可以弥补MIDAS（m，k）模型不能对样本外数据进行预测的不足，且能根据最新公布数据进行预测，如：当预测步长h小于3时，可以利用最新更新的月度数据对季度GDP增长率进行实时预测，当预测步长大于3时，可进行样本外预测。

为了比较MIDAS模型相对于传统模型的优势，本文选取多项式分布滞后模型（PDL）作为基准模型。如表6所示，无论是受参数限制的还是无约束的MIDAS模型，相比较基础模型都展示出更精确的预测，如步长为1时，MIDAS模型和U-MIDAS模型预测效果对比基准模型提升35%和56%，一定程度上说明混频数据模型能提取高频变量的高效信息。随着步长的增加，两种模型的预测能力开始下降，尤其对于因子2，两个模型的预测效果开始减退，甚至逊于基础模型，其中主要是由于MIDAS模型基于滞后时期数据信息，当预测步长过大时，所利用的信息过早，不能对当前和未来的经济发展做出很好的模拟。在步长为1的情况下，因子1基于两种模型的预测效果最佳，最小均方根误差为2.951和0.642，其模型的参数估计如表7所示。在检验性水平为5%的条件下，因子1基于MIDAS预测的拟合优度为68.8%，基于UMIDAS模型的拟合优度为70.2%（由于参数过多，不再展示），显然这个拟合程度不足。

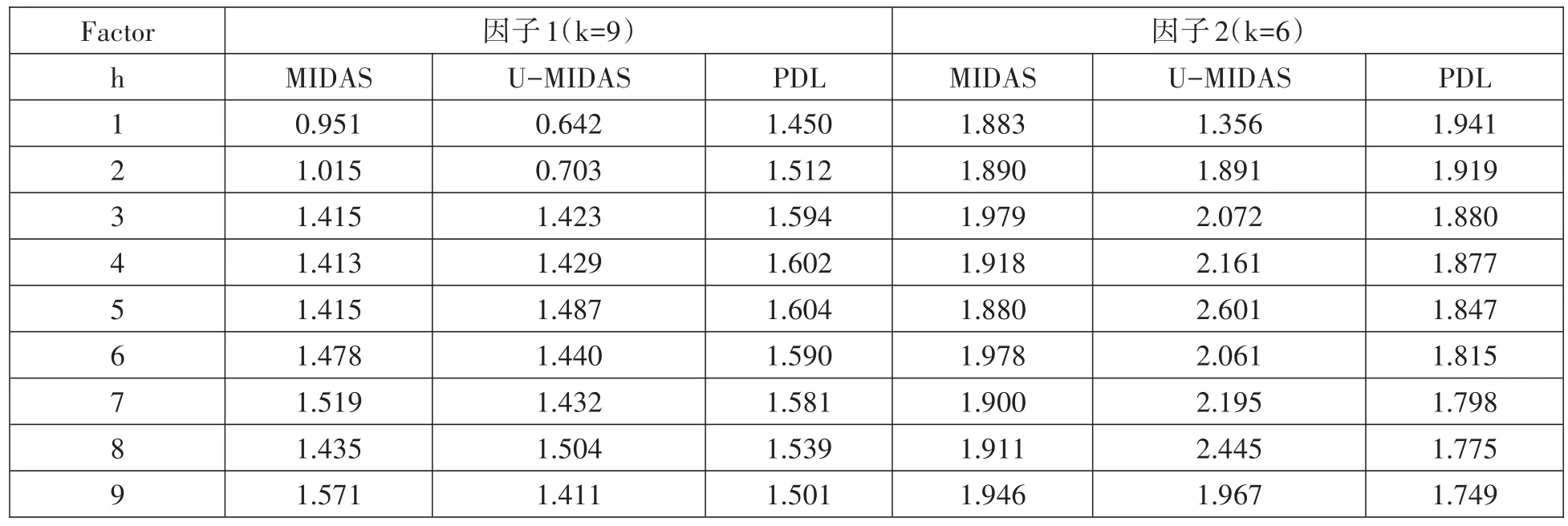
表6 在最优滞后阶数下两个因子的RMSE

表7 最优模型下参数估计结果

（四）加入自回归项的AR-MIDAS（3，k，h）-（p）模型

对于宏观经济变量模型预测，常常加入自回归项来减少经济系统惯性的影响，因此，本文在模型MIDAS（3，9，h）的基础上加入AR（p）项，用以作为预测精度的对比。

根据表8中的预测误差以及表9中最优参数估计结果，可以看到，加入自回归项后，除了因子一前两步预测外，无论是受限制的混频数据模型还是非限制参数的混频模型，其预测能力都有了明显的提高，且其拟合精度亦有所提升，上升到80.3%和92.0%。

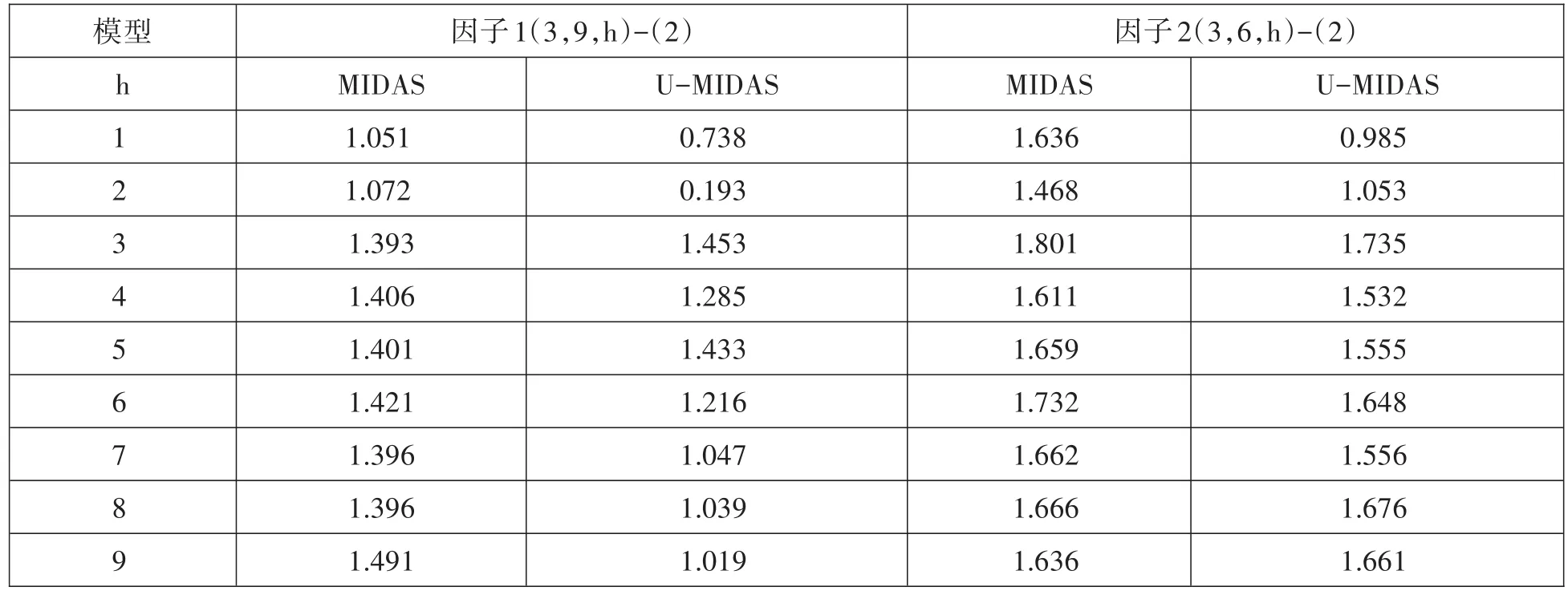
表8 基于AR-MIDAS（3，k，h）-（p）模型的预测误差

表9 加入自回归项的最优模型参数估计

综上所述，本文认为从众多指标中提取因子变量对于模型的预测效果有明显提升，主要是由于因子变量是高频变量信息的提取，在某种程度上能代替原始变量数据，面对宏观数据指标的增加，很难再利用单个指标对模型效果进行估计。当然，提取因子的方法不一，因子个数也有所差异，但相对于单变量预测，充分利用众多变量中的有效信息能提高模型的预测精度。

四、结论

本文通过基于先行指标、一致指标以及滞后指标构建变量，并提取因子，建立经典的MIDAS模型，并对比比较了非限制MIDAS模型的预测效果。通过比较在不同滞后阶数以及步长下的模型的预测能力发现以下三点。

1.对于预测季度GDP的指标来说，先行指标和一致指标更有优势。二者的平均预测误差优于滞后指标，由此说明滞后指标由于数据波动的延迟，对模型的预测效果不显著。

2.在从众多指标中提取因子后，因子变量由于携带原始变量绝大多数信息，在预测上有了明显改善。尤其对于本文中提取的因子1，其贡献度达到65%，其预测精度高于几乎所有单一指标，从而证实从指标中提取有效因子的可行性。

3.非限制MIDAS模型在滞后阶数较短的情况下，其预测精度和拟合效果要优于受限制的MIDAS模型，且随着预测步长的增加，非限制MIDAS模型预测能力开始下降，表示非限制MIDAS模型更适用于短期预测。