量子启发式优化算法的尺度动态调速机制

穆 磊，王 鹏

（1.西南民族大学计算机科学与工程学院，四川成都 610041；2.电子科技大学计算机科学与工程学院，四川成都 611731）

1 引言

优化问题是一种选择特定方案以在特定条件下实现最佳目标的方法，被广泛用于军事、工程、管理等领域，是人工智能和其他技术领域的基石［1］.

多尺度量子启发式谐振子优化算法（Multiscale Quantum-inspired Harmonic Oscillator Algorithm，MQHOA）是一种受量子物理过程启发的优化算法［2］，源于量子退火（Quantum Annealing，QA）派生的量子优化理论［3］，其理论体系和应用领域都得到了广泛的关注，在数据聚类［4］、任务分配［5］、功率自适应控制［6］等方面都有应用.

王鹏等人［2］定义了MQHOA 算法波函数，提出了算法基本物理模型.随后，零点能量和量子隧穿效应的分析极大地发展了该算法框架［7］.文献［8］证明了波函数定理和尺度减半策略的有效性，通过量子算符从理论上解释了多尺度的必要性.随后，一些工作补充了算法理论体系［9］.应用方面，基于MQHOA 的具有多级分辨率的多模优化分区算法显示出良好的性能［10］.MQHOA还被用于选择聚类中心，通过波函数的概率变化将高能级降到低能级来找到最佳的聚类和聚类中心［4］.韩虎等人［11］将云计算任务调度方案与MQHOA 的采样位置建立关联，在CloudSim 平台上实施并获得了优于比较算法的调度方案.

尺度因素是大多数智能优化算法的重要组成部分，用于调整算法在解空间的搜索粒度.现有大量MQHOA 的研究工作使用尺度减半策略，即尺度除以2作为下一个尺度值.该方法可以实现不同粒度的搜索，但缺乏灵活性，未考虑实际进化过程中不同的算法状态具有不同的搜索粒度要求，无法实现自适应调整.另外，由于高斯分布的聚集效应，高斯采样生成的候选解会聚集在采样中心区域附近.如果当前采样中心位于定义域的边界，可能导致采样点因聚集效应以大概率集中在边界附近，使得算法陷入早熟收敛.这也是本文要解决的问题.

本文的主要贡献如下：（1）将适应度进化利用率作为尺度动态调速的依据，通过尺度调节因子动态改变尺度调节速度，以达到探索与开发的平衡；（2）根据映射点、采样中心点和生成点之间的位置关系，定义了2种不同的边界映射策略，测试了不同尺度调节因子参数组合对性能的影响；（3）采用一种动态可接受误差的评估机制，通过数据自身特征来计算可接受误差，以此计算成功率，评估算法稳定性；（4）将改进算法与MQHOA 及对比算法在基准测试函数上进行了比较，实验结果表明改进算法有效地提高了MQHOA的性能.

2 多尺度量子启发式谐振子优化算法

MQHOA 的理论基础的核心思想是优化空间中的搜索过程与量子空间中的粒子运动具有相似性［12］.根据QA 派生的量子优化理论［3］，当量子系统收敛到基态时可以得到目标函数的极值［13，14］.因此，优化问题可以理解为在有约束势阱的量子系统中寻找基态.

2.1 量子运动与优化问题的映射

量子系统中，波函数随时间和空间变化的方程被称为薛定谔方程.其中，定态薛定谔方程描述了粒子在势阱中受不含时Hamiltonian 约束的运动，它可以看作从量子力学的角度来描述优化问题的工具，形式如下［15］：

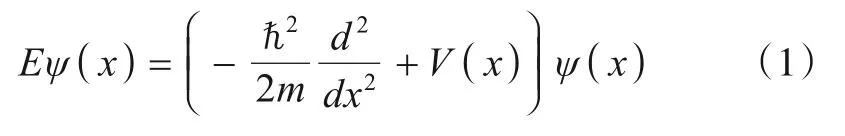
其中，ℏ 表示简化的普朗克常数，m表示粒子质量，状态ψ(x)的能量特征值表示为E.波函数ψ(x)的二次方对应于粒子的概率分布，可以被认为与最优解的概率分布相关［12～14］.

理论上，可以通过求解薛定谔方程得到基态波函数，然后得到最优解的概率分布.与量子计算机相比，经典计算机实际处理的优化问题通常涉及非常大的Hilbert 空间，薛定谔方程的推演在这种条件下是不可行的.MQHOA 将复杂目标函数f(x)的全局优化问题转换为求解不同尺度下谐振子势的基态波函数问题，使整个理论系统具有可操作性，原理如图1所示.

从图1 可以看出，MQHOA 采用势阱等效和谐振子势能近似，使薛定谔方程可以近似求解.定态薛定谔方程变为

图1 MQHOA基本原理框图

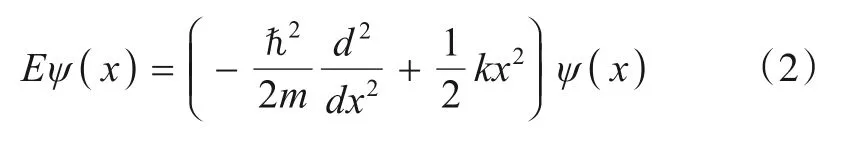
其中，k是弹性系数.

2.2 MQHOA算法流程

MQHOA 的具体实现框架由3 部分组成，即能级稳定、能级下降和尺度调整，具体流程如图2所示.

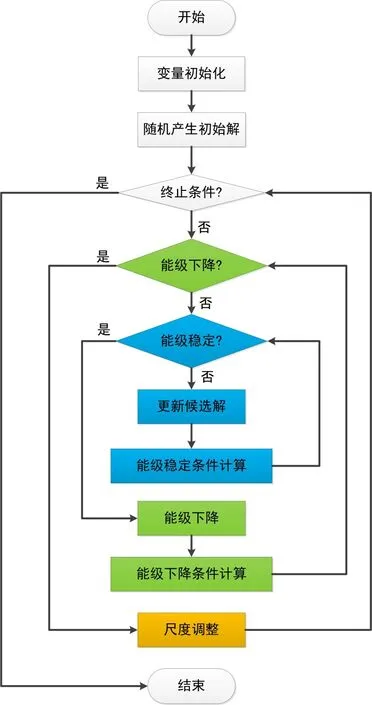
图2 MQHOA算法流程图

从图2 可以看出，能级稳定是算法的基本进程，达到能级稳定条件后将转入能级下降阶段，依此类推，直到在该尺度下达到基态.尺度调整后，在新搜索粒度下重复该循环过程.通过这样的机制，全局优化问题转换为多尺度的基态收敛问题.

关于MQHOA 的详细理论推导和实现细节可以参考文献［14］.

3 尺度调整速度调节的改进方法

本节定义了尺度调节因子以及进化效率的评估指标，改进了边界映射策略以提高算法性能，随后，详细阐述了MQHOA中尺度调整速度调节的改进算法.

3.1 术语

定义1fs定义为尺度调节因子，用作尺度调节的控制量.

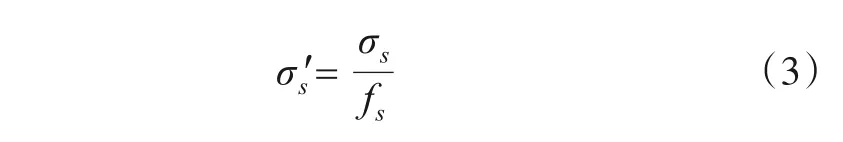
定义2适应度进化利用率rfe定义为下式中适应度变化与进化次数变化的比率：

3.2 边界反弹映射策略

进化算法中一般使用边界映射策略处理候选解超出定义域的情况.MQHOA 中采用直接截断策略.本方法将越界点根据其与临近边界点的位置关系，反弹回定义域特定区域.根据映射点、采样中心点和越界点的位置，可以定义2种不同策略.

在定义之前给出以下符号定义：越界采样点位置为xb，采样中心位置为xc，边界反弹映射策略生成的点位置是xg.定义域上界为ub，下界为lb.2 种边界反弹映射策略定义如下.

定义3生成点和越界采样点在采样中心的同一侧，称之为正向反弹策略.在这种情况下，(xb-xc) ×(xg-xc) ≥0.设α是均匀分布在（0，1）上的随机数，则可以根据以下公式生成新点：

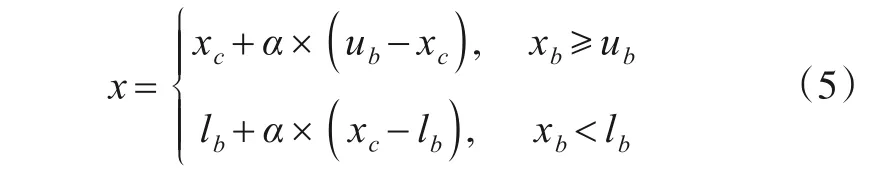
定义4生成点和越界采样点在采样中心的不同侧，称之为负向反弹策略.在这种情况下，(xb-xc) ×(xg-xc) ＜0，可以根据以下公式生成新点：

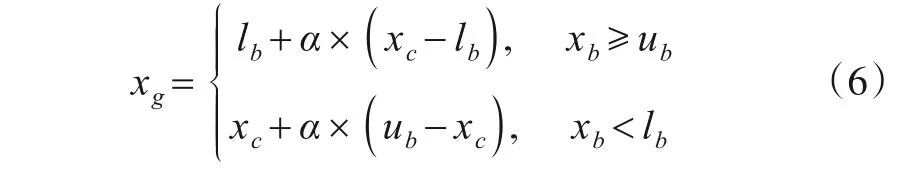
图3 是2 种反弹映射策略的示例.图3 中，浅色点表示采样中心点，蓝色点是越界采样点，超出了定义域的范围.正向反弹策略将点映射到采样中心的同侧，如图3（a）所示的绿色点.负向反弹策略将点映射到采样中心的相反一侧，表示为绿色点，如图3（b）所示.

图3 边界映射策略

3.3 尺度调整的速度调节

进化算法的探索和开发存在均衡问题.如果使用固定尺度调节因子fs调整尺度，则可能会丢失某些尺度上的测量值，也有可能在某个尺度浪费过多资源.MQHOA 中尺度减半策略对应的尺度调节因子是2，该策略以此作为速度调整变化的基准.

本方法通过尺度调节因子来改变尺度调整的速度.当适应度值变小时，获得适应度值并记录对应的进化数，通过式（4）来计算适应度进化利用率.一旦适应度进化利用率发生变化，尺度调整速度将动态调节.

如果新适应度进化利用率小于原有适应度进化利用率rfe，则表明进化平均收益在下降.此时，尺度应迅速下降，以加强新尺度下的探索，尺度调整采用加速因子fa，其值应大于2.如果大于rfe，则表明进化平均收益在增加.此时，尺度应缓慢下降，以促进该尺度附近的开发，尺度调整采用减速因子fd，其值应小于2.

定义a为尺度调整因子的控制向量，尺度调整基向量为f，则尺度调整因子fs可以表示为a和f的内积：

3.4 算法实现框架

本文提出的方法在MQHOA 的框架基础上进行改进，其伪代码如算法1所示.

4 数值模拟讨论

PSR 和NSR 分别表示具有正向和负向反弹策略的尺度动态调速方法，与以下优化算法进行综合比较：MQHOA，精简烟花算法（Bare Bone FireWorks Algorithm，BBFWA）［16］，量子行为粒子群优化算法（Quantum Particle Swarm Optimization，QPSO）［12］和标准粒子群优化算法2011（Standard Particle Swarm Optimization 2011，SPSO2011）［17］.

4.1 基准测试函数

基准测试函数用来验证不同优化算法的总体性能，它们都被表述为最小化问题，并根据其重要物理特性和形状相似性进行分组，如表1所示.

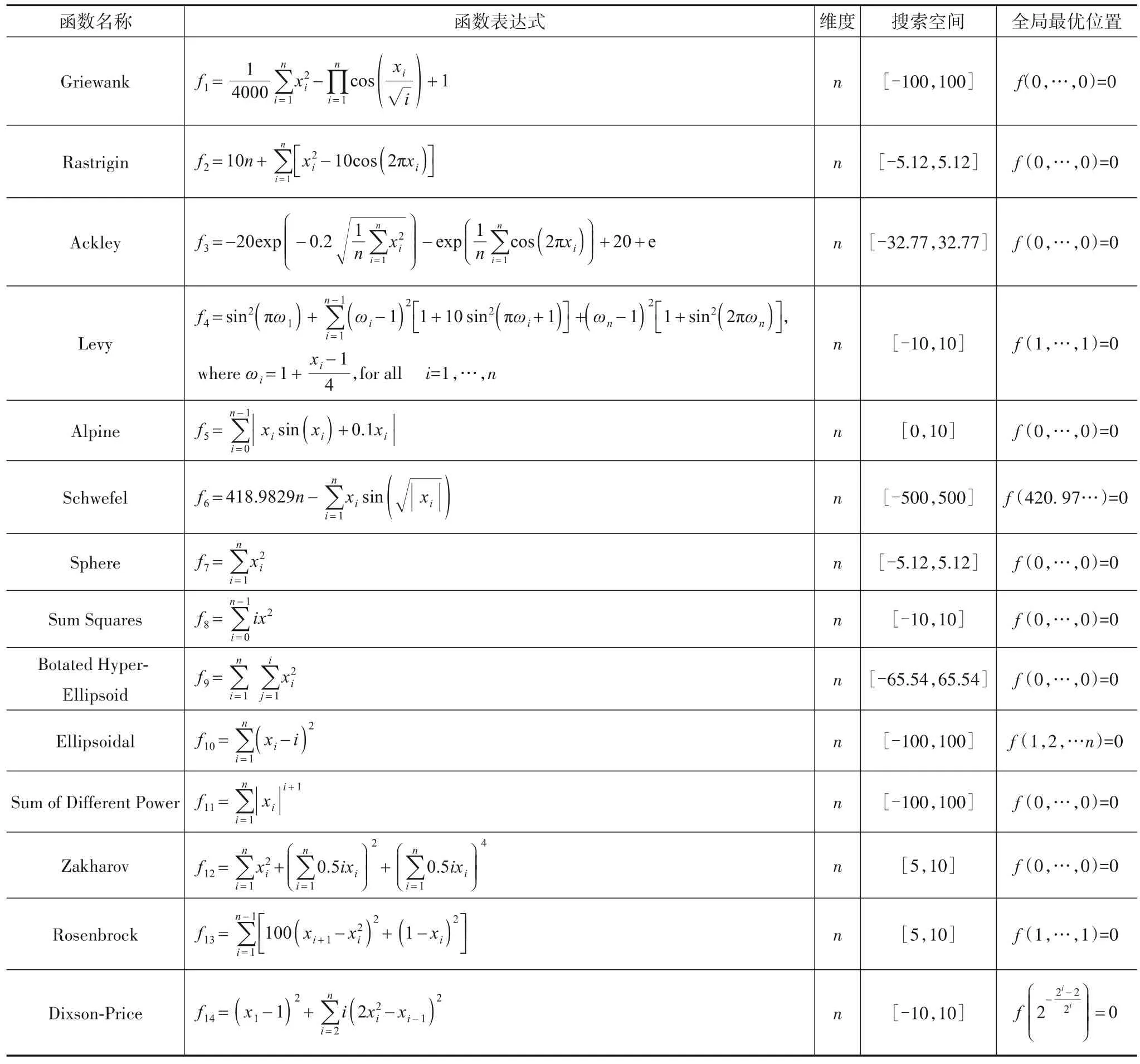
表1 基准测试函数

这些基准测试函数分为2 类.函数f1～f6是多模函数，它们都具有许多局部最小值，可以测试优化算法跳出局部最优值的能力.函数f7～f14是单模函数，它们只有一个全局最小值，具有不同的形状，例如碗形、谷形等，主要测试算法对不同问题的快速收敛能力.

4.2 实验参数设置

本文针对每个基准测试函数的30维问题进行了实验，最大进化次数设为10 000×维度，每个实验重复运行51次.所有比较算法的种群规模均设置为40以进行公平比较.每种算法中的参数设置均基于相关文献.BBFWA 中的Ca和Cr分别设置为1.2 和0.9，在QPSO 中考虑了线性递减的收缩膨胀，其中a1和a2分别设置为1和0.5.SPSO2011 的参数选自文献［17］.在MQHOA 及其改进算法中，k表示探针或个体的数量，设置为40.所有数值模拟都在8 GB 内存的Intel i7 6700 CPU（3.4 GHz）和Windows 10 的计算机上通过64 位版本的MATLAB R2018a实现.

4.3 尺度调节因子参数分析

在比较算法之前，应先确定合适的尺度调节因子fs.本文使用不同取值下尺度调节因子来求解30维问题基准测试函数的实验，统计分析参数组合对两种边界映射策略的影响.

为了便于计算，限制了参数组合的数量，采用网格搜索确认参数组合.其中，fa从2.1 变化至2.9，步长为0.2；fd从1.1 变化至1.9，步长为0.2.在这种情况下，2 种边界映射策略改进的MQHOA算法总计有5×5种参数组合.针对每个基准测试函数进行51次运行，计算每种参数组合对应的误差.所有实验运行完成后，统计2种改进算法的不同参数组合中，每种参数组合下误差不高于原始MQHOA的函数数量.随后，固定尺度调节因子组合中的一个参数值，然后将另一参数所有对应结果求平均值.由于函数数量为整数，向下取整直接保留整数部分.

2种边界映射策略的结果以不同的颜色区分，如图4所示，其中虚线是趋势线.

图4 尺度调节因子统计结果

如图4所示，根据尺度调节因子的定义以及基准参考值的选取不难看出，当尺度调节因子与2越接近的时候，加速或减速越慢；当尺度调节因子与2差距越大时，加速或减速越快.

对于负向反弹策略，当fa较大时，仅在较少数量的测试函数上实现性能提升.fd较小时也会发生相同的情况.数据表明，大幅度的加速和减速不利于负向反弹策略的性能提升.负向反弹策略位置调整相对较大，快速调整尺度会导致特定尺度下的搜索不足.

正向反弹策略显示出相反的趋势.当fa较大时，在大量测试函数上实现性能提升.fd的值与实现性能改进的函数数量负相关.结果表明，在正向反弹策略中，尺度调整应相对较快地加速和减速.该映射策略将点映射到越界点附近的定义域内，如果速度调节相对较慢，则会在特定尺度上消耗资源，从而影响多样性和进化利用率，使性能受到影响.

4.4 与其他方案的比较和讨论

将2 种改进算法与一些常见优化方案在基准测试函数的30 维问题中进行比较，评估不同优化算法的误差和成功率.在NSR 中fa和fd设置为2.1 和1.7，在PSR中fa和fd设置为2.3 和1.1.这些参数值参考第4.3 节中的实验结果进行设置.

4.4.1 误差分析

不同优化算法的误差结果显示在表2 中.每个单元格中的数据均由3部分组成：平均值、标准差（第一个括号中）以及该误差在所有算法中的排名顺序（最后一个括号中的数字）.

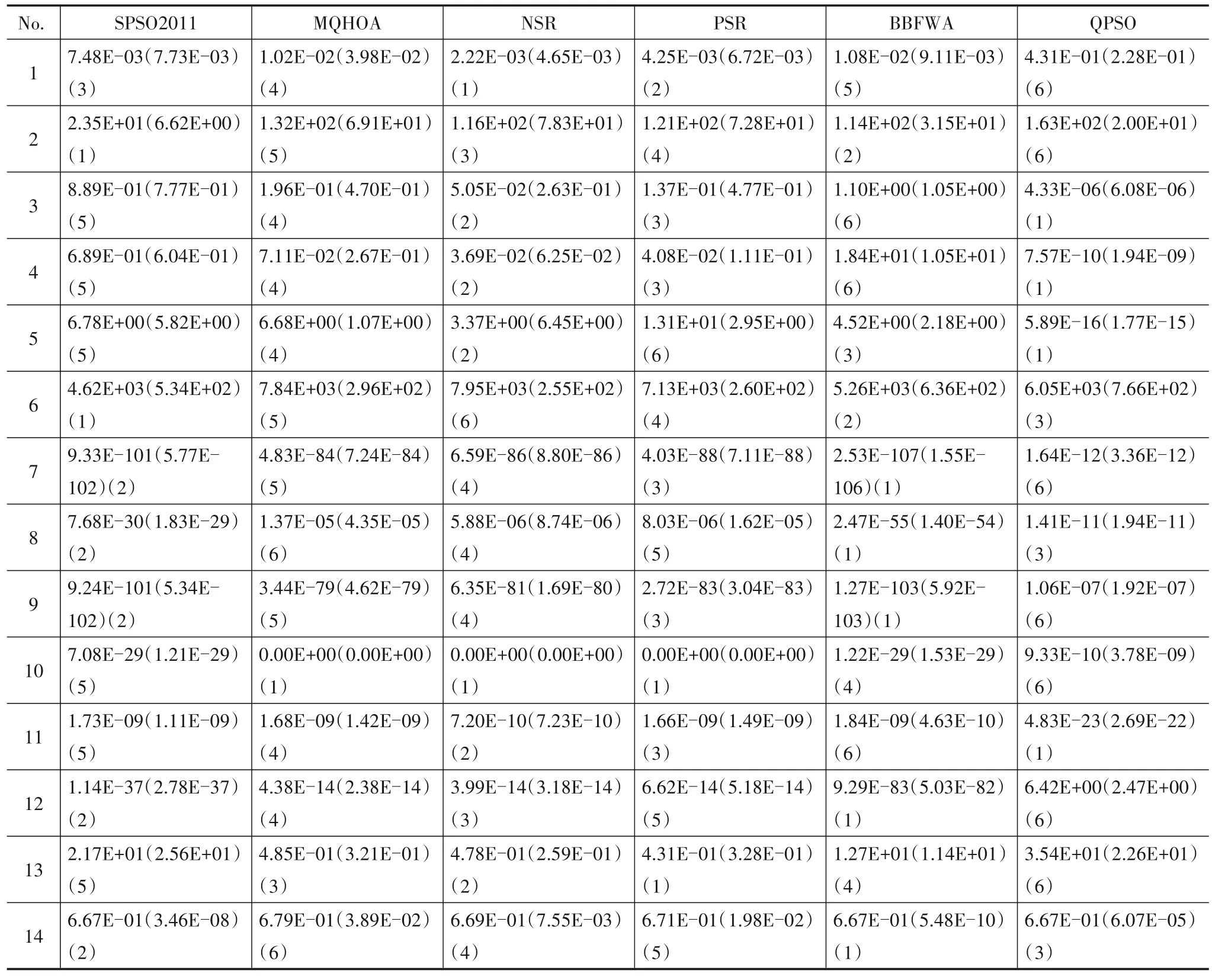
表2 基准测试函数上的误差结果

为了更清楚地观察整体性能，将每个算法误差均值的排名按照单模函数、多模函数和所有函数分类进行平均.

图5 显示了所有平均误差的平均排名（Average Ranking，AR）.根据中央极限定理，AR～N((k+1)/2，(k2-1)/12n)，其中k是对比算法数量，n是测试函数数量［18］.单模函数，多模函数以及所有函数上AR 的先验标准差（Prior Standard Deviation，PSD）为0.6，0.69和0.46.

如图5所示，BBFWA 在单模函数上排名第一，其次是NSR 和SPSO2011.NSR 在多模函数中排名第一，紧随其后的是QPSO 和SPSO2011.在所有函数上，NSR 排名第一，BBFWA 排名第二，之后是SPSO2011.虽然BBFWA 在f7，f8，f9，f12，f14等函数中排名优势显著，但在某些函数上排名太低.NSR 由于在不同函数上的均衡排名而胜出.

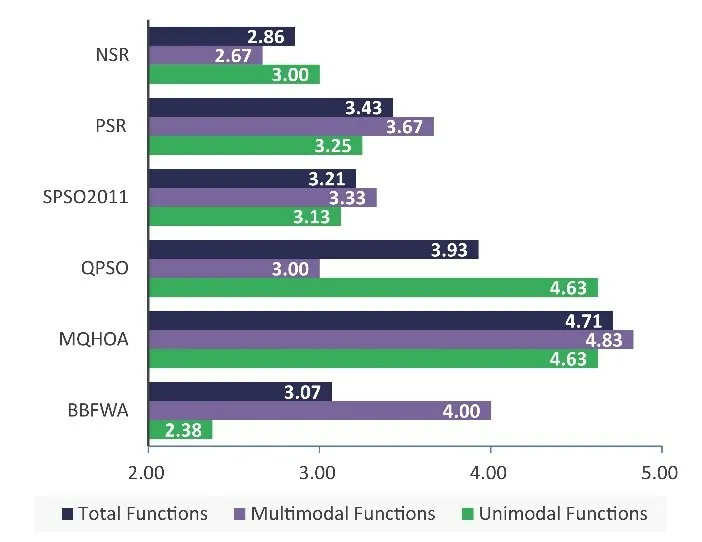
图5 基准测试函数上的误差均值平均排名

图6 显示了部分基准函数上不同算法平均误差的统计信息.其中MQHOA 和BBFWA 分别用M 和BBF表示.

图6 部分基准测试函数误差均值箱形图

根据箱形图的分析结果，NSR 在除f2之外的所有基准测试函数上均具有良好的稳定性.NSR 在f1，f3，f4，f7，f9，f10，f12，f13上表现出稳定性和良好性能之间的平衡.在f5和f11上，NSR在性能和稳定性方面的表现并不是最好的，但也排在前列.

4.4.2 成功率分析

成功率rs可用于衡量算法的可靠性，它被定义为达到可接受误差范围内的运行次数占运行总次数的比例，可以按下式计算：

其中，naccept和ntotal分别表示达到可接受误差范围内的运行次数和运行总次数.对于每个函数，计算所有算法误差均值的平均数，将其作为可接受误差eaccept：

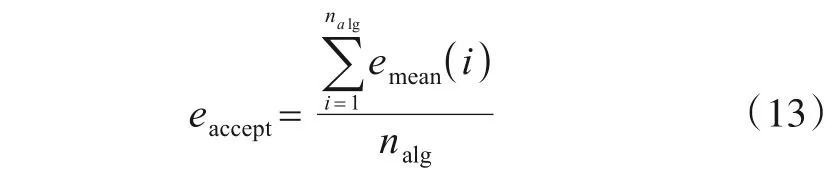
其中，nalg表示对比算法总数表示第i个算法的误差均值.

成功率结果显示在表3中，括号中的数字表示其在测试函数上的排名.

表3 基准测试函数成功率

如表3 所示，SPSO2011 在所有算法中的10 个函数上表现最佳.NSR 再次显示出其均衡性，它在7 个函数上表现最佳，在3 个函数上均获得第二名，在11 个函数上获得高于0.8 的成功率，这是所有算法中的最佳结果.SPSO2011在10个函数上的成功率都是1，但在其他函数上的成功率小于0.6.BBFWA 在8 个函数上的成功率均大于0.8.总体而言，NSR 在更多函数上获得了更高的成功率.

各个算法按照不同的基准测试函数进行成功率排名，并分别按照单模函数、多模函数以及所有函数的类别分别计算成功率的平均排名，结果显示在图7中.

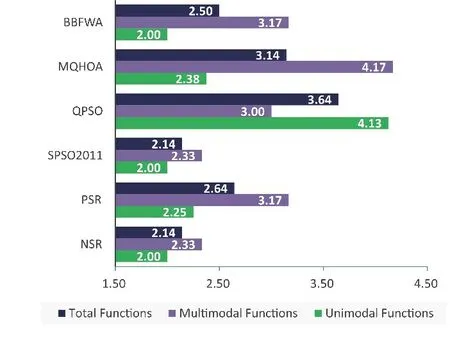
图7 基准测试函数上成功率平均排名

该图显示了NSR 和SPSO2011 在单模函数、多模函数和所有函数上成功率的平均排名均优于其他方案.NSR在不同的测试函数上表现出更好的均衡性.BBFWA由于在多模函数上性能不佳而在所有函数上获得第三名.

4.4.3 计算复杂度

算法1中生成候选解的时间复杂度为O(nprobendim)，其中，nprobe和ndim分别表示探针数量和问题维度.当探针数量固定时，此时间复杂度随问题的维度线性增加，即时间复杂度为O(ndim).此外，尺度调整速度调节的时间复杂度不会随问题的维度而变化，即时间复杂度为O(1).通过分析整个算法，可以看到其他部分的时间复杂度最多为O(ndim).从以上分析可以得出，在不考虑目标函数影响的情况下，本文提出的算法总体上具有线性时间复杂度.

将每个算法在相同的基准测试函数上执行51 次，然后计算该基准测试函数上算法的平均执行时间，结果显示在表4中，括号中的数字表示其在基准测试函数上的排名.

表4 基准测试函数平均执行时间（单位：s）

从表4 中可以看出，BBFWA 的平均执行时间在各种基准测试函数中显示出绝对的优势.NSR 在大多数基准测试函数中排名第二，在3个基准测试函数中排名第三.因此，NSR的排名仍然不错.PSR在平均执行时间上也表现良好，它在14个函数的8个函数中排名前三.

各个算法的平均执行时间排名按照单模函数、多模函数和所有函数上的分类计算平均值，结果如图8所示.

图8 基准测试函数执行时间均值平均排名

从图8 可以看出，BBFWA 在所有函数中均排名第一，其次是NSR 和PSR.MQHOA 和QPSO 的平均执行时间平均排名接近，而SPSO2011 排名最后.对于每种算法，不同类型函数之间的排名得分差异很小.在不同类型函数中，所有算法的排名顺序都没有改变.

4.4.4 讨论

这些对比算法具有不同的特性.SPSO2011 对原始粒子群优化有两大改进，即自适应随机拓扑和旋转不变性.这些措施带来了良好的全局搜索能力，并阻止了早熟现象的产生.BBFWA 的结构非常简单.它使用动态爆炸半径进行搜索，并采用贪婪策略来更新候选解.QPSO通过压缩-扩展系数来调整算法的收敛过程，从而可以在全局搜索和局部搜索之间取得平衡.其候选解的采样函数是对应于δ势阱的双指数分布.该采样分布的累积效应强于高斯分布，因此局部搜索能力强于MQHOA.MQHOA 利用高斯分布的波函数生成候选解，并通过调整尺度以不同的分辨率搜索解空间.本文所提出的算法主要在边界映射策略和尺度调整速度调节方面改进了MQHOA.

边界映射策略可以使算法具有更大的概率在定义域内有效搜索.负向反弹策略将越界点反弹到采样中心的另一侧并远离采样中心，具有更强的量子隧穿作用，并探索了更广阔的区域，获得了更好的多样性.通过分析rfe的变化，动态选择fa和fd以调节尺度调整的速度.负向反弹策略将点出界映射到远离采样点的区域，在该区域采样的可能性很小.应该缓慢减小尺度，以微调搜索分辨率进行开发.较小的fa和较大的fd可以获得更好的结果.正向反弹策略将外部越界点映射到采样点附近，该区域被采样的可能性更高.如果速度调节相对较慢，则可能会消耗过多的搜索资源，从而影响rfe和候选解的多样性，导致性能下降.因此，应迅速进行尺度调整，这可以通过较大的fa和较小的fd来实现.第4.3节中的实验结果验证了上述分析.

为了更直观地观察各算法排名对比情况，把不同算法在各个评估指标上的整体排名进行综合统计分析，如表5所示.

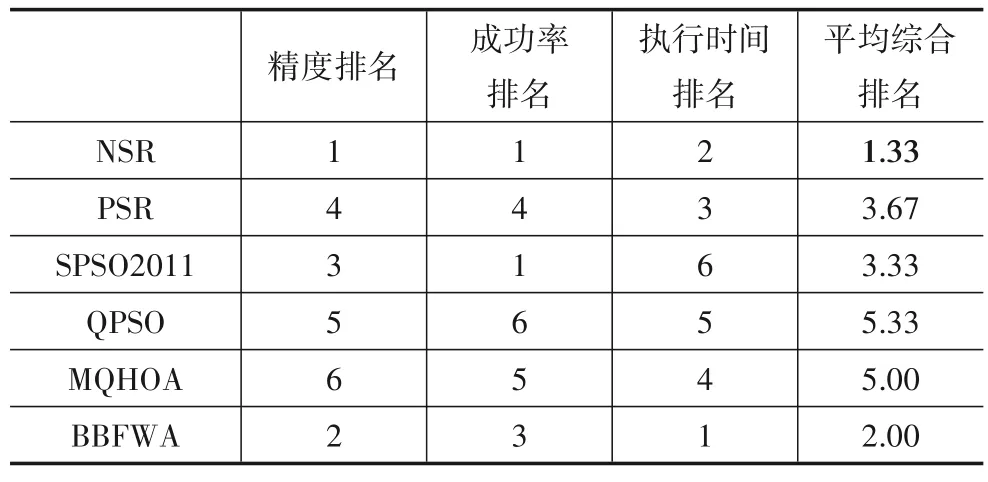
表5 不同算法的平均综合排名

可以看出，在所有算法中，NSR 在平均误差方面排名最高，NSR 和SPSO2011 在成功率方面排名最高.BBFWA 在平均执行时间方面有很大的优势，其次是NSR.在多个维度的综合评价中，NSR 获得了最高的平均综合排名.从性能，效率和稳定性的总体平衡来看，排名结果显示了NSR的优势.总体而言，NSR与对比算法相比具有较强的竞争力.

5 结论

本研究的重点是改善尺度资源的利用效率和解的多样性，以提高算法性能.具体而言，采用适应度进化利用率表征特定尺度下的资源利用效率，用作动态调节尺度调整速度的标准.提出了2种不同的边界映射策略来提高多样性.通过使用不同参数组合的实验，统计分析尺度调节因子对算法的影响，实验结果表明2种改进算法通过适当的速度调节可以提升MQHOA的性能.

为了评估所提出方法的整体性能，与MQHOA 以及其他流行算法在基准测试函数上针对30维问题进行了实验比较.计算平均误差、成功率和平均执行时间并分别进行排名.实验结果表明，尺度动态速度调节可以通过平衡探索和开发来提高MQHOA的性能，边界映射策略对性能改进有积极作用，负向反弹策略会带来更大的竞争力.

本文提出的算法仍然存在一些局限性.首先，改进算法的平均执行时间仍有提升空间.此外，增加了算法中的参数数量，参数的各种组合会带来不同的效果，因此有必要分析参数组合以获得更好的性能.另外，尺度反映了优化算法搜索粒度，多种尺度调整策略和规则值得进一步研究.这些问题都是未来的研究重点.