一种履带式管道检测机器人的转弯算法研究

石红梅，侯 伟，谢文霞

(1.陕西能源职业技术学院； 2.咸阳特种设备检验所，陕西 咸阳 712000)

0 引言

现代计算机、网络及通信等技术的发展使得“智能+网络”[1-3]主导模式已成功应用于教育、工业、商业和国防等众多领域，特别是给机器人领域[4-5]带来了改革与创新。为了满足完成管道大修检测、降低人工操作风险的要求，管道机机器人[6]应运而生。管道检测机器人可分为轮式机器人、蠕动式机器人和履带式机器人等。

与轮式机器人相比，履带式机器人与管壁的接触面积更大，因此具有更大的牵引力[7]。然而，由于管道中的约束极其复杂，需要对机器人运动状态进行严格分析，从而提高控制精度。管道机器人的很多研究都集中在机器人的自主操作上，这需要基于大量的传感器信息[8-12]。一般来说，机器人与管道内壁的接触位置不在同一平面内，这表明机器人在管道内的运动分析和控制分析比管道外的分析更困难。尽管目前对弯曲管道和变形管道的研究很多，但由于弧形管道空间的限制和机器人自身参数的限制，履带式机器人在管道中运动的分析仍有不足之处。首先，对管道中的车轮或履带的分析需要依赖三维空间，这导致机器人在弯管中的运动姿态以及与管道的接触程度很难详细分析；其次，大多数分析只关注机器人进入弯管后的持续时间，不涉及从直管到弯管的过渡阶段。

为了解决传统算法自主控制能力和环境适应性不足的问题，该文提出了一种基于上述管道机器人和相似结构管道机器人的转弯方案。该方案主要适用于伸缩杆结构的履带式管道机器人。该算法能使机器人伸缩杆随环境变化，实现稳定运行；它还可以确保机器人在更大的管径范围和更大的重量负载下稳定运行。该算法有助于大型输油管道中的机器人检测，通过简化机器人模型来实现。通过分析履带与管壁的接触点，建立了二维方程，得到了机器人在直管进入弯管过程中的约束条件和在弯管中的约束条件；通过三维分析，得出了满足足够牵引力的三履带支脚在运行中的最佳位置和三履带支脚的伸缩状态。根据机器人的3条腿位置，推导出机器人的3条腿速度比。根据履带速度与偏置角之间的关系，结合各种传感器的信息进行综合处理，建立了机器人的偏转角和机器人主控芯片的输出模型。同时，该文对算法模型进行了仿真和实验，证明了算法的可行性。

1 运动学分析

图1所示为机器人示意图。为分析机器人的整个运动过程，首先介绍2个坐标系：世界坐标系和机器人自身坐标系。对于世界坐标系，将沿着管道方向设置为Z方向，将地面的法线方向设置为X方向，将XOZ平面的法线方向设置为Y方向；对于机器人自身坐标系，将机器人的3条腿分别命名为f1(上)、f2(左)和f3(右)，其中f1始终与机器人坐标系的X轴方向一致，Z轴是机器人的前进方向。

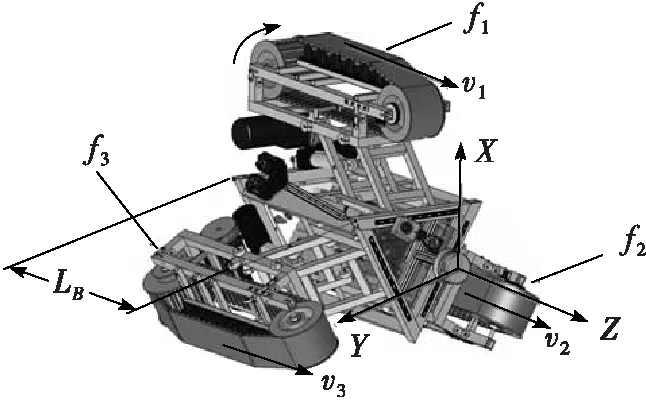
图1 机器人示意图

1.1 直管运动分析

机器人在直管中的运行状态示意图如图2所示。根据图2(a)所示机器人横截面，如果忽略轨道的宽度，并将机器人的轨道视为刚体，则机器人与截面上管道内壁之间只有3个接触点。为此，可将机器人抽象成一个矩形，并俯视管子内部的运动。如图2(b)所示，矩形左右两侧的边界是机器人腿f3和机器人腿f2，矩形的中心线是机器人腿f1。因此，在直线管道中，矩形两侧的边界也是机器人和管道之间的接触点。机器人的中心与管道的中心轴重合。同时，假定机器人的3条腿的速度保持不变，分别表示为v1,v2和v3，机器人的中心速度为v，则有：

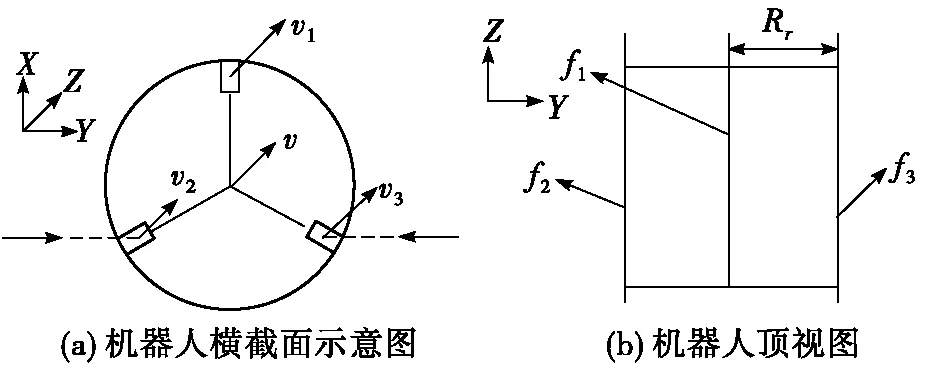
图2 机器人在直管中的运行状态示意图

v1=v2=v3=v

(1)

1.2 弯管运动分析

在2D分析中，假设管道是理想的弯管，将机器人的转向运动分为2步：第1步是从直管进入弯管，第2步是在弯管中移动。下面对2个步骤的运行进行详细分析。

1.2.1 入弯运动模型

图3所示为机器人从直管进入弯管过程示意图。

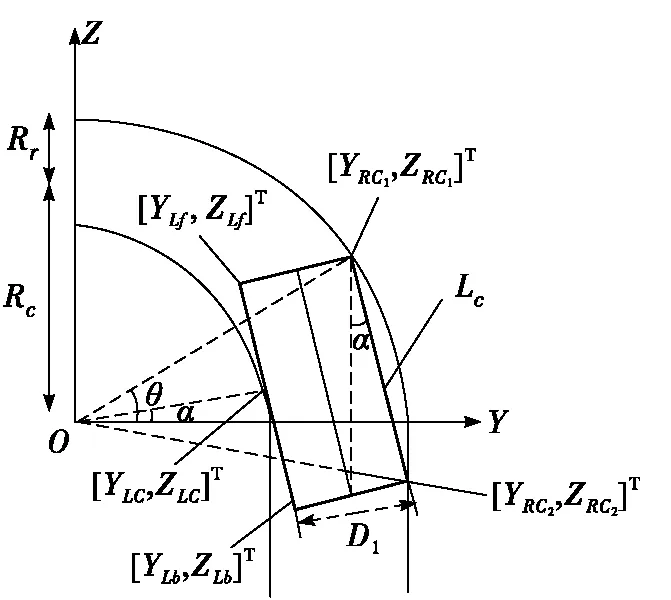
图3 机器人从直管进入弯管过程示意图

受曲线的空间约束，机器人的驱动模块与管道的接触点将减少，机器人的中心不再与中心轴重合。下面分析3个接触点的坐标。首先，将接触点定义为[YLC,ZLC]T，[YRC1,ZRC1]T，[YRC2,ZRC2]T。需要注意，f1和管道在不同的位置的接触点具有不同的量，具体定义为{[YLC1,ZLC1]T,[YLC2,ZLC2]T,…}。此外，矩形的右顶点定义为([YRf,ZRf]T,[YRb,ZRb]T)，左顶点定义为([YLf,ZLf]T,[YLb,ZLb]T)。

如图3所示，令矩形末端到原点的直线与Y轴角度为θ，交点[YLC,ZLC]T到原点O的直线与Y轴之间的角度为α，Rc为从管道轴线到原点的距离，R是管道半径，Rr为管道中心轴到履带接触点的水平位置。因此，R和Rr之间的关系定义如下：

(2)

[YRC1,ZRC1]T=[(Rc+Rr)cosθ,(Rc+Rr)sinθ]T

(3)

[YLC,ZLC]T=[(Rc-Rr)cosα,(Rc-Rr)sinα]T

(4)

[YRC2,ZRC2]T=[(Rc+Rr),(Rc+Rr)cosθ-Lccosα]T

(5)

需注意，矩形左边界的方向与管道内表面的切线方向相同，从切入点到原点的直线垂直于矩形左边界。因此，矩形右边界线方程ZR可描述如下：

根据平行线斜率相同的原理，矩形左边界线方程ZL可推导如下：

(7)

根据平行线原理，两平行线之间的距离可以计算如下：

(8)

(9)

上述公式表明，在机器人从直管进入弯管的过程中，机器人履带之间的距离随着机器人的运动而变化，该运动学关系表征机器人在弯管运动过程中需要满足的条件。

1.2.2 形变运动模型

考虑到机器人3个履带的拉伸状态不同，机器人模型将从矩形形变为平行四边形。图4所示为机器人形变过程示意图，机器人增加了一个角度β，因此点[YRC2,ZRC2]T可更新如下：

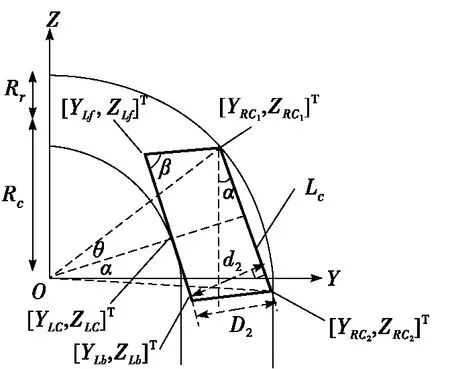
图4 机器人形变过程示意图

[YRC2,ZRC2]T=[(Rc+Rr),(Rc+Rr)sinθ-Lccosα]T

(10)

同理，右边界线ZR和左边界方程ZL可描述为：

(11)

(12)

此时，根据平行线原理，两平行线之间的距离d1=D1。然而，由于抽象模型为平行四边形，机器人的约束会发生变化，距离约束D2定义如下：

(13)

1.2.3 完全转弯模型

当机器人点[YRC1,ZRC1]T进入YOZ坐标平面的第一象限时，表示机器人已完全进入弯道。图5所示为机器人完全转弯过程示意图。此时，[YRC1,ZRC1]和[YLC,ZLC]T的坐标没有变化，因此根据三角形公式，有以下公式成立：

图5 机器人完全转弯过程示意图

LC1=(Rc+Rr)sin(θ-α)

(14)

(15)

[YRC2,ZRC2]T=[(Rc+Rr)cos(α-γ),(Rc+Rr)sin(α-γ)]T

(16)

此时，右侧边界线计算如下：

(17)

因此，机器人在弯管中移动的约束条件可以等效于矩形左右两侧之间的距离d2，计算如下：

(18)

根据机器人的机械结构特点，其弯曲约束条件D3描述如下：

(13)

2 优化模型

根据以上分析，f2和f3不同程度的收缩可能导致不同的角度α和β。当获得f2和f3的最佳拉伸条件时，可根据机器人形状获得f1的位置，并根据此时的位置进一步获得3条履带速度关系。因此，如何获得最佳拉伸条件成为一个亟待解决的重要问题。

图6所示为机器人在弯管中的运动状态。3条实线分别表示机器人履带f1，f2和f3在管中的移动路径的法线。从机器人的机械结构可知，如果获得机器人在管道中的2个履带模块的运动路径，则可以通过管道本身的约束获得第3个履带的运动路径。假设3个履带到机器人中心的距离为L1，L2和L3，两者之间的夹角为120°，由余弦定律可知：

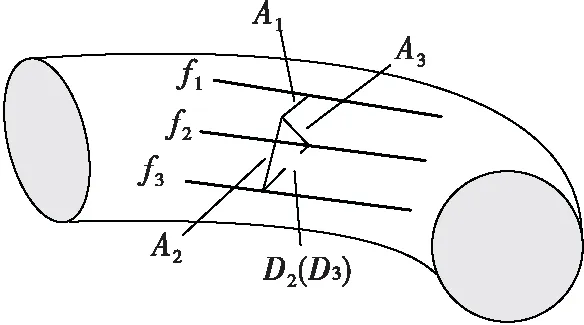
图6 机器人在弯管中的运动状态

(14)

d=Dsinβ

(15)

为了将履带的膨胀程度与约束结合起来，需要分析L和伸缩杆之间的关系。图7所示为履带和主机架的抽象视图，忽略主机支架的宽度，令伸缩杆装置的距离为X，机架的部分长度为a1，整体长度为A1，机架与中央底座装置上伸缩杆装置之间的距离为c，机架与中央底座装置下边框之间的角度为ε。因此，X和L之间的关系可描述如下：

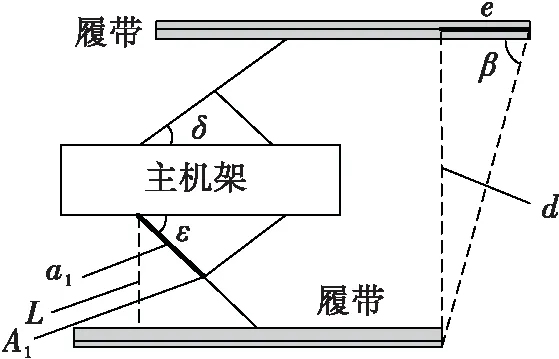
图7 履带和主机架的抽象视图

(16)

(17)

同理,令机架与中央底座装置上边框之间的角度为δ。与ε计算方法类似,假设伸缩杆装置的变化为dε,则角度β与伸缩杆装置延伸长度e的关系为：

a[cosε-cos(ε+dε)]=e

(18)

(19)

(20)

式中：D为D2或D3。

3 实验与分析

3.1 数值模拟

该文使用MATLAB来模拟机器人的弯曲速度，从而确定上述弯曲算法是否符合实际运动过程。仿真运行环境如下：酷睿i7 CPU，内存为64G ARM的联想服务器,操作系统为64位Win10。此外,仿真时相关参数定义如下：机器人的长度为530 mm，宽度为400 mm，机器人轨道的厚度为177 mm，管道的半径为1100 mm，管道中心到弯管中心的距离为2200 mm。图8所示为机器人通过90°弯管时的速度偏移角关系曲线。

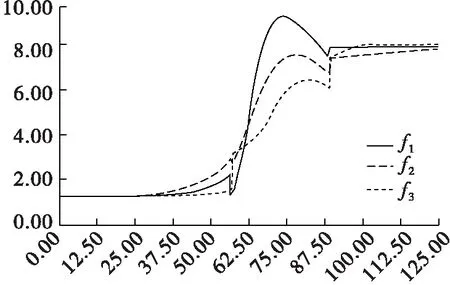
图8 机器人通过弯管时的速度偏移角曲线

对仿真数据进行分析可以看出，在90°的角度下，机器人的单足速度在管道中移动时几乎呈线性变化，并且在弯曲过程中一直缓慢加速。弯管角度越大，机器人的3条履带速度非线性程度越小。外履带速度的变化比内履带更明显。仿真结果表明，3条履带的速度存在一个跳跃点，该点主要由机器人从不完全到完全进入弯道引起，同时，跳跃现象随着弯道曲线的增加而减小。

3.2 实物验证

为了验证算法的合理性，在内径为1100 mm的管道上进行了实物试验(如图1所示)。该机器人由3个履带模块组成，在圆周方向上以120°的间隔对称排列。每只履带垂直于管道内壁，并配有驱动电机，因此3个履带的速度相互独立。同时，利用速度编码器采集3个履带的速度，并基于薄膜压力传感器采集履带的压力值，将结果记录在机器人主控芯片携带的SD卡中。图9所示为机器人3个履带在实际运行中的速度变化图，数据采样率为10 Hz。该图显示了几次实验后获得的时间和速度的平均值。由于PID的稳定速度控制，机器人可以在平均6 s的时间内通过曲线，整体速度波动很小。实际结果与仿真结果相似。仿真结果进一步验证了该模型在实际应用中显示出良好的优越性，为履带机器人合理通过弯管起到一定借鉴作用。

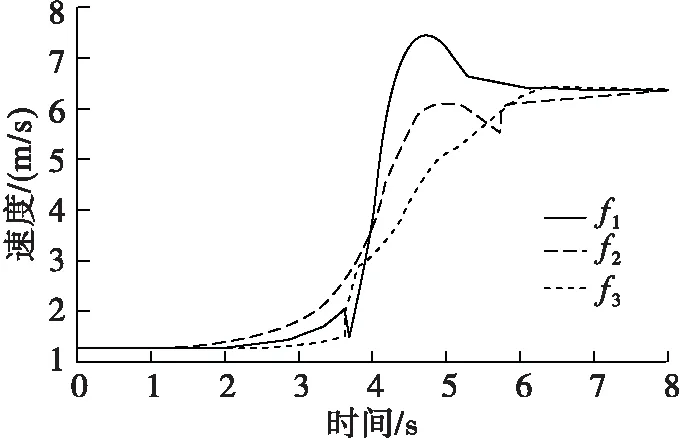
图9 3个履带在实际运行中的速度变化图

4 结论

该文基于运动学模型对履带机器人在弯管中运动进行了研究与分析，提出了一种机器人弯管转弯方案。该方案将机器人的转向运动分为2步：第1步是从直管进入弯管，第2步是在弯管中移动。所提方案对履带机器人弯管移动技术研究提供了一定借鉴作用。