一种周期信号波形识别及参数测量装置的设计

殷理杰，张文初，魏丽君

(湖南铁道职业技术学院，湖南 株洲 412001)

0 引言

在信号处理中，对周期信号的参数进行测量具有非常重要的意义。在测量数值参数时，如果能准确的对波形的类型进行识别，便能够针对该类波形的特点，采取更为合适的采样、数值计算策略，从而能够改善参数的测量精度。

该文以STM32为主控完成了一个能够对周期信号波形进行识别并测量参数的装置。为拓宽被测信号范围，使用2级4档放大电路做信号调理，使得装置的测量范围提升到50 mVpp～10 Vpp，频率1 Hz～50 kHz。最大值、最小值、峰峰值、有效值、频率等主要测量参数误差不大于1%。

1 整体方案设计

装置整体框图如图1所示。2级放大器、钳位及比较器直接使用一个4运放LF347实现。放大倍数的调整通过模拟开关CD4052切换不同的反馈电阻实现。参数显示使用320×240分辨率的TFT屏。主控芯片为STM32F103VE，丰富的外设资源能够满足本装置的设计需求。钳位电路将连接STM32F103VE的片上ADC接口，比较器输出将连接片上定时器输入IO，以便使用片上资源完成相应功能。

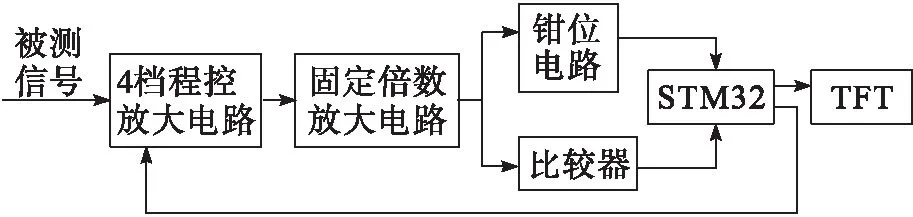
图1 整体框图

2 硬件电路设计

为满足1 Hz～50 kHz、50 mVpp～10 Vpp的采样需求，需要设计程控增益放大器，使得输出信号最大值不大于3.3 V，最小值不小于0 V，以满足STM32F103片上ADC的采样需求。该文中设计一个2级4档位放大倍数放大器，如图2所示。

图2 放大器电路图

由于LF347的增益带宽为4 MHz，当需要放大10倍时，其通频带仅为400 kHz，对50 kHz信号进行放大时，必然丢失高频分量，导致波形失真。因此，设计采用2级放大形式，第一级(U1A)最大放大倍数为3.3倍时，通频带约为1.21 MHz，第二级(U1B)固定放大3.03倍时，通频带约为1.32 MHz。采用2级放大电路设计后，能够显著降低高频信号放大的失真。

在第一级放大电路中，反馈电阻通过模拟开关CD4052选择，最大放大倍数3.3，最小放大倍数0.068。与第二级放大电路组合后，最小放大倍数为0.22，最大放大倍数为10。

当输入信号在峰峰值范围为3～10 V时，使用0.22倍档位，输出信号范围0.66～2.2 Vpp；输入信号在500 mVpp～3 Vpp时，选用1倍放大；输入信号在100～500 mVpp时，选用3.63倍放大，输出信号范围为363 mVpp～1.815 Vpp；输入信号在50～100 mVpp时，选用10倍放大，输出信号的范围为500 mVpp～1 Vpp。

输入信号为双极性信号时，需要通过添加直流偏置，时被采样信号不小于0 V。该部分功能使用U1D电路实现。为便于测频，通过U1C组成的比较器，将任意波形转变成矩形波，并确保最小值不小于0 V。

输入信号为50 mVpp和50 kHz正弦波时，经过电路得到的波形如图3所示。

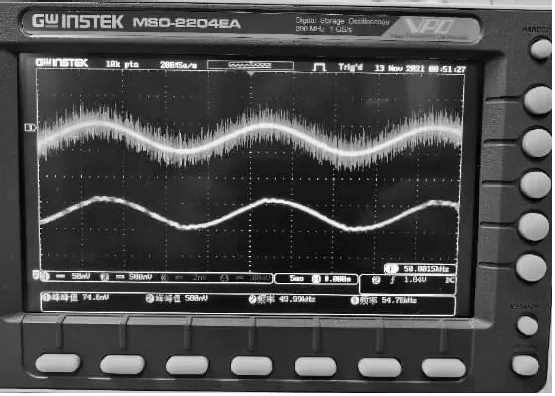
图3 实测波形

3 软件设计

3.1 频率测量

被测信号转换成矩形波后，可直接使用STM32F103的PWM输入模式，能够准确的测量频率和占空比。由于被测信号频率范围宽，需要进行分档测量。对于200 Hz以上的信号，使用12 MHz的计数频率；小于200 Hz的信号，使用10 kHz的计数频率。

当计数频率与被测频率较为接近时，定时器的CCR1和CCR2的值比较接近，此时测频误差较大，应切换为高采样频率。当被测频率太低时，由于不能监测到合适的边沿停止计数，因此会触发定时器的溢出中断，此时需要降低计数频率。测频部分程序流程图如图4所示。

图4 测频程序流程图

3.2 信号采样

为保证ADC的输入信号不大于3.3 V，STM32F103初始化后默认将放大倍数设置为0.22。完成一次采样后，计算被测信号的幅度，并选择合适的放大倍数，使输入信号的电压范围尽量在500 mV～2 V范围内。

采样使用ADC的DMA模式完成，ADC的外部触发转换信号为TIM3的更新事件。设置TIM3的分频系数和计数个数，则能够对采样频率进行设置。由于采样频率范围广，因此需要根据测得的被测信号频率，选择合适的采样频率。为了能够更好的恢复被采样信号，采样频率不低于被测信号频率的20倍，即每个周期不少于20个采样点，并设定一次采样长度为1000个采样点。采样频率与被测信号频率如表1所示。

表1 被测信号频率与采样频率对照表

STM32F103片上ADC的最快转换速度为1 μs，即1 MHz，因此使用传统方式按20倍于被测信号的采样频率，50 kHz被测信号已是能够采样的最高频率。如果需要对超过50 kHz的周期信号进行采样，则可以使用多周期采样。简而言之，就是在每个周期内，仅完成一个采样点的采样，20个周期后，则可以恢复出周期信号。如图5所示，被测信号周期为，假设为第一个采样时刻，则第二个采样时刻为，即为所在位置。使用多周期采样，能够使用转换速率较低的ADC完成对高频周期信号的有效采样。

图5 多周期采样示意图

为确认采样的正确性，将STM32F103采样的数据通过串口发送到PC，并通过Excel绘制出波形。如图6所示为使用多周期采样策略对50 kHz正弦波进行采样，等效采样频率1.25 MHz。

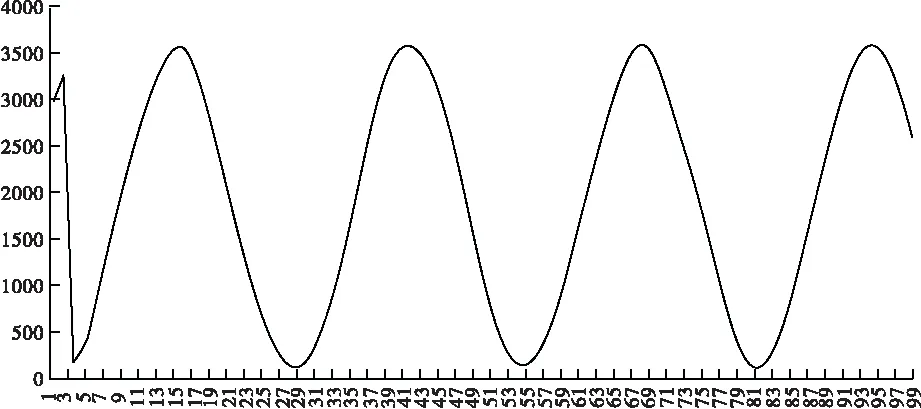
图6 多周期采样50 kHz信号波形

3.3 波形识别

采样完成后，可计算出被测信号有效值，通过计算有效值与幅度之比，可辨别正弦波、三角波、正弦波。但是，这种传统的识别方法对采样的精度要求非常高，同时也对信号调理电路的精度提出了很高的要求，有效值和幅度存在少量变差时，就会影响波形识别的准确性。此外，该种方式不能很好的识别三种基础波形以外的波形。

波形识别本质上属于分类问题，是机器学习中最简单的问题。为提高波形识别的抗干扰能力，引入机器学习中的k最邻近(kNN)算法用于波形识别。kNN算法的思路非常简单：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别[]。波形识别时，每个采样点都可以认为是一个特征点，因此kNN算法能够应用于波形识别。

将被识别信号经过幅度和频率的归一化后，可以求其与模板波形的距离，根据kNN的思想，被识别信号与距离最小的模板具有相同的波形，由此完成波形识别。

为验证算法的可行性，使用Matlab生成了5种波形模板，如图7(a)所示。增加期望为0.1的正态分布随机数作为噪声到波形模板，如图7(b)所示，用于模拟待识别波形。

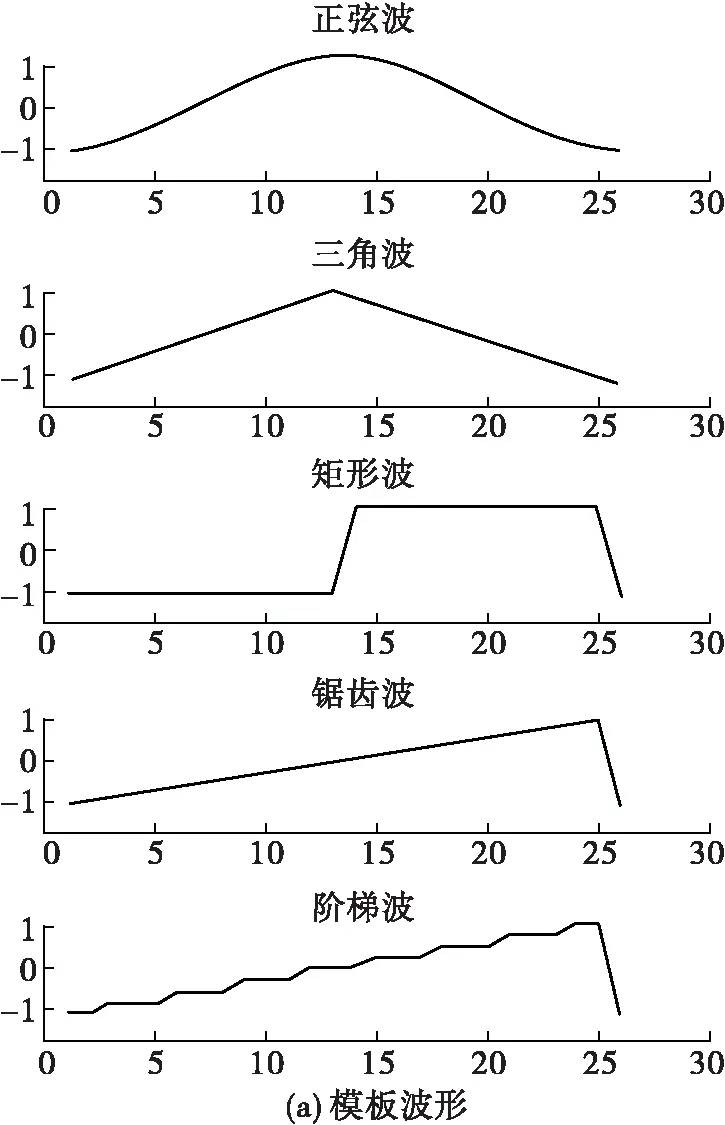
图7 测试波形图

经过kNN计算后，可得到如图8所示结果。横坐标为模板编号，1为正弦波，2为三角波，3为矩形波，4为锯齿波，5为阶梯波。加扰正弦波与正弦波模板距离最近，即最为匹配，与三角波也比较接近，但还是显著大于与正弦波的距离，与矩形波的距离已超过坐标范围。加扰三角波、加扰矩形波、加扰锯齿波、加扰阶梯波都能被准确识别出，故确认了kNN算法用于波形识别的可行性，且该方法可推广用于各类波形识别，只需准备相应模板即可。

图8 kNN识别结果

此外，算法在实施过程中，可省略距离计算中的开平方运算，以此减小运算量，提高识别速度。

4 实验测试

为验证装置的实际测试效果，对频率及波形识别测试结果如表2所示。峰峰值测试结果如表3所示。对50 kHz和2 Vpp正弦波进行测量的实物图如图9所示。

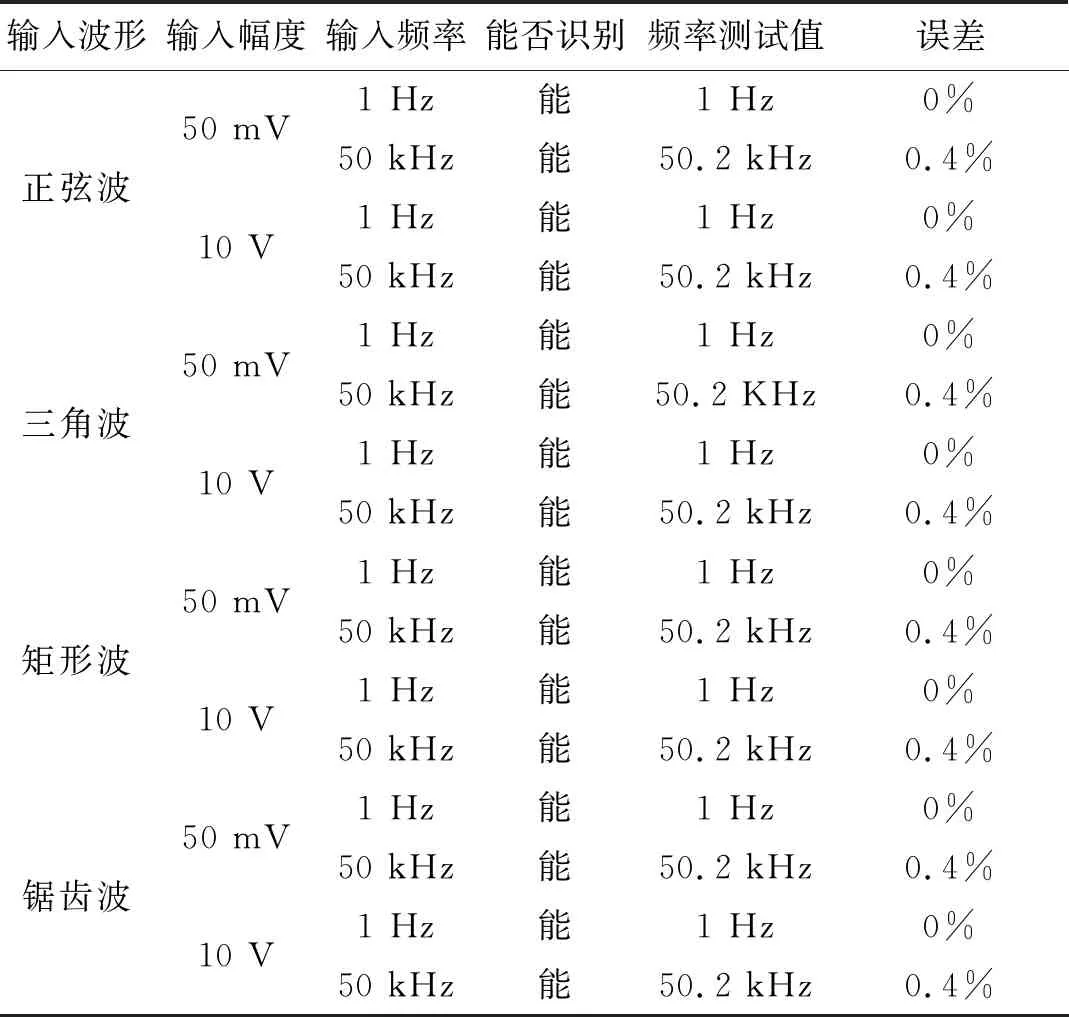
表2 频率及波形识别测试

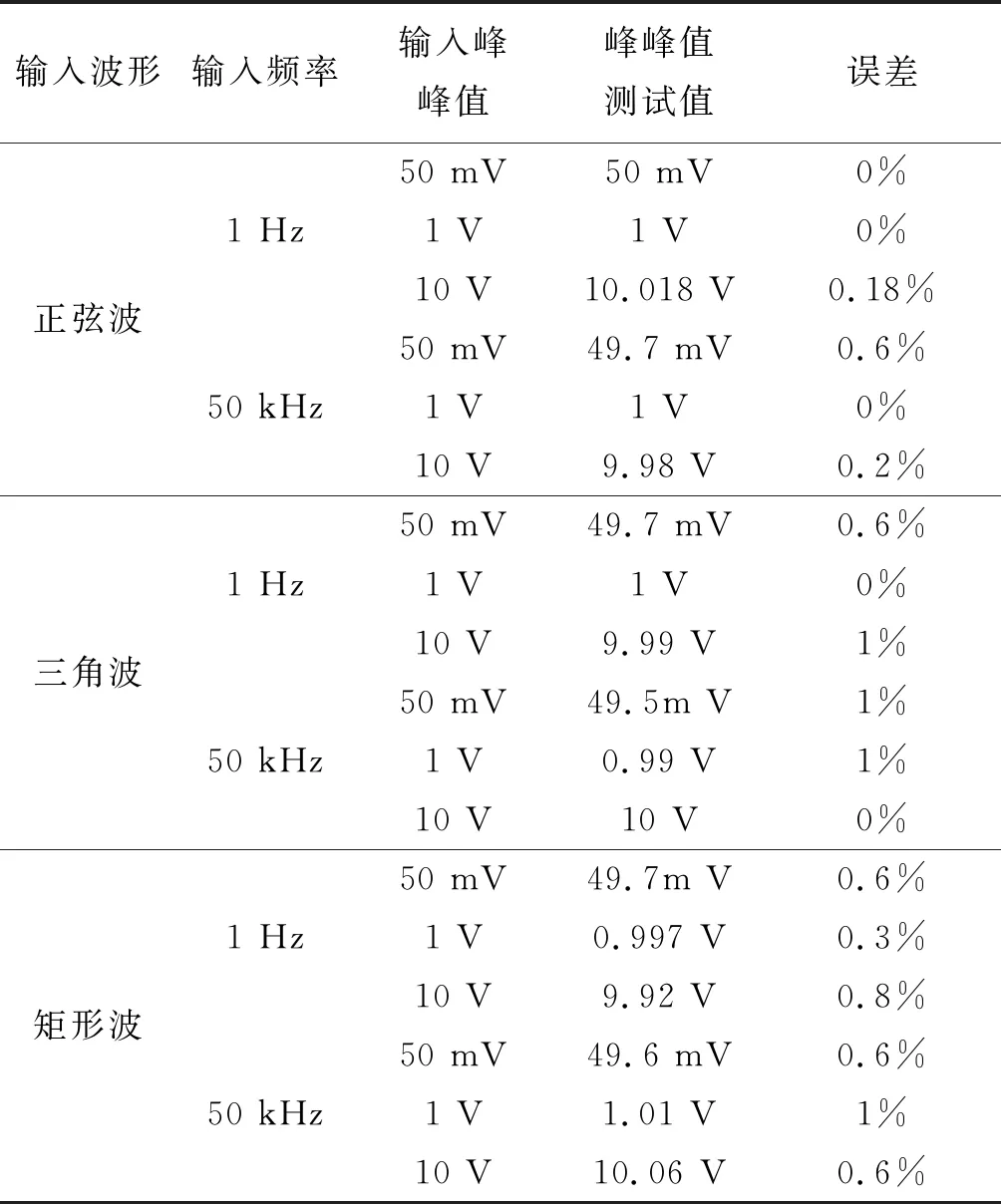
表3 峰峰值测试

图9 实物图

5 结论

经过设计，完成了模拟信号采集电路、4档位2级放大电路，通过多周期信号采样策略以及kNN算法，实现了对周期信号进行波形识别及参数测量。经过反复实验，该装置能够对50 mVpp～10 Vpp，1 Hz～50 kHz信号的参数进行有效测量，且误差不超过1%，很好地达到了预期效果。