汶川县水磨镇地震动场模拟

张 皓,江华伟,李宏男,2,孙 威

(1.沈阳建筑大学土木工程学院,辽宁 沈阳 110168;2.大连理工大学建设工程学部,辽宁 大连 116024)

据不完全统计,在全球大陆的大地震中,约有25%～30%发生在中国[1]。2008年我国四川省汶川县发生8.0级强烈地震,震中烈度高达11度,波及范围广,地震导致汶川县下属各级村镇区域的震害极其严重。我国地震动参数区划图主要是按城市区域进行分区划分,未考虑城市区域与村镇地区的环境差异,无法精确反映村镇区域的特点。因此有必要针对村镇区域开展地震动场模型的研究,为村镇区域的防震减灾提供理论依据。

目前,国内外学者对针对地震动场模拟开展了大量的研究工作。I.A.Beresnev等[2]将有限断层模型随机点源法相结合当中提出了随机有限断层法模拟地震动场。H.Mittal等[3]采用随机有限断层法模拟了印度北阿坎德邦和尼泊尔边界处发生的5.4级地震。ZHOU Hong等[4]对随机有限断层法进行修正,进而模拟了2013年芦山7.0级地震的地震动场。王国新等[5]回顾总结了国内外关于地震动模拟的相关方法,采用随机有限断层法合成汶川各网格点的地震加速度时程,并绘制了加速度等值线图,分析了地震动的分布特点。大量震害调查结果表明,地震动扭转分量也会导致建筑物发生严重破坏[6]。李钢等[7]在对汶川地震村镇建筑结构震害调查研究中发现,村镇建筑破坏形式具有多样性,有些破坏模式可明显看出是地震动扭转分量造成。L.Knopoff等[8]根据地震发生时的震源机制展开研究,结果显示,地震发生时,断层发生破裂的不平衡扭矩能够产生一种扭转波,进而导致场地发生扭转变形。王君杰等[9]分别从定量和定性两个方面展开了对薄壁圆柱回转壳结构在地震动扭转分量作用下的地震反应分析的研究,结果发现,针对结构反应贡献大小,扭转分量主要和结构高度、结构高度比、回转半径以及壳的刚度有关。

在地震动场模拟及结构抗震分析中仅考虑平动分量可能会低估地震的破坏力。笔者以汶川县水磨镇(东经103.427°,北纬30.937°)作为区域研究对象,基于该区域地震原始数据通过概率法开展地震危险性分析,采用随机有限断层法模拟合成该区域各网格点的地震动平动分量,基于地震动平动分量建立地震动场。在此基础上基于弹性波动理论方法得到与该区域内各网格点地震动平动分量相对应的地震动扭转分量,建立基于地震动扭转分量的地震动场。

1 地震危险性分析

1.1 地震带划分

以汶川县水磨镇为中心,半径约150 km的地理区域,即东经101.5°～ 105.5°,北纬29.5°～ 32.5°。根据四川及邻区地震区划图[10],对水磨镇地区影响最大的地震带主要有甘南川北地震带、四川盆地地震带和川滇块体地震带。

1.2 地震重现关系

地震重现关系又称为震级-频度关系,通常由G-R关系式来表述:

lgN=a-bM.

(1)

式中:M为震级;N为震级大于M的地震总数;a、b为统计常数。

通过统计分析川滇块体地震带、甘南川北地震带和四川盆地所发生历史地震的次数和震级之间关系,即可得到各地震带的震级-频度关系如下[11]:

lgN=3.700-0.688 9M.

(2)

lgN=3.665-0.733M.

(3)

lgN=4.155-0.888M.

(4)

1.3 潜在震源区地震空间分布函数

将以上三个地震带的地震活动参数中年平均发生率分配给各潜在震源区,将各潜在震源区按震级进行分档,再将各地震带的地震年平均发生率按不同权重分配给各潜在震源区,结合文中实际情况,采用文献[10]中在水磨镇研究区范围内的各潜在震源区地震空间分布函数。

1.4 基岩加速度峰值衰减关系

采用西南地区、美国西部地区地震烈度衰减关系和美国西部地震动衰减关系得到西南地区长轴和短轴基岩水平峰值加速度衰减关系[11]如下:

log10A长袖=-0.334 9+1.380 7M-0.066 5M2-2.192 0 log10(R+2.529 2exp(0.333 4M)).

(5)

log10A短袖=-1.520 6+1.453 9M-0.071 5M2-1.849 9 log10(R+2.529 2exp(0.333 4M)).

(6)

1.5 地震危险性分析结果

在地震带划分后可以看出,各个地震带上的地震活动在时间和空间上均呈现非均匀分布的特征,地震活动发生的时间过程在进行概率性地震危险性分析时可近似表达为分段泊松分布;各地震带的震级上限和下限可分别表示为muz和m0,t年内出现震级为muz和m0之间地震的年平均发生率可用v0表示,因此在该地震带t年内发生k次地震的概率为

(7)

震级概率密度函数为

(8)

式中:β=bln10,b为地震重现关系中的b值。

(9)

式中:Δm为震级分档步长。

将各地震带划分潜在震源区,则各个震级档的地震发生在各地震带的各潜在震源区在空间上呈非均匀分布,用fj,mj作为各潜在震源区的空间分布函数来表示这种地震空间分布不均匀性。潜在震源区的个数用Ns来表示。地震带上的地震对场地影响的地震动参数为A,则A超过已知值a的概率为

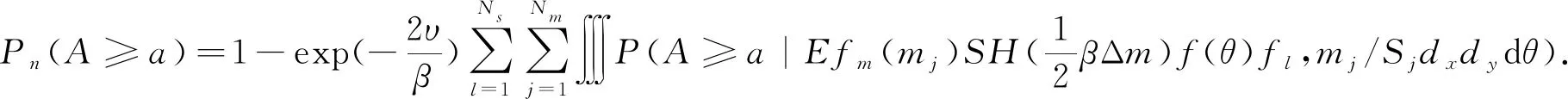
(10)

式中:P(A≥a|E)表示第i个潜在震源区发生特定事件时场地处地震动值超过a的概率;f(θ)为等震线长轴方向的分布函数。

综合Nz个地震带对场点的影响得:

(11)

基于以上方法得到水磨镇地区地震危险性分析结果见表1。

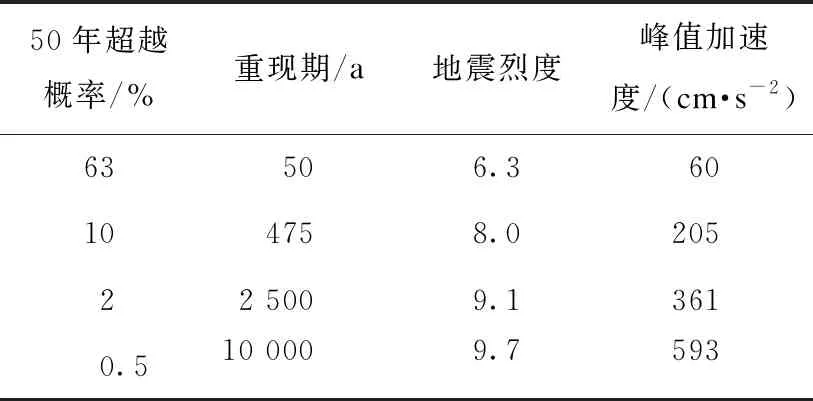
表1 水磨镇地区地震危险性分析结果

水磨镇地区50年超越概率分别为63%、10%、2%、0.5%的加速度反应谱曲线如图1所示。该地区50年超越概率63%的地震烈度为6.3度,PGA=60 cm/s2;超越概率10%的地震烈度为8.0度,PGA=205 cm/s2;超越概率2%的地震烈度为9.1度,PGA=361 cm/s2;超越概率0.5%的地震烈度为9.7度,PGA=593 cm/s2。

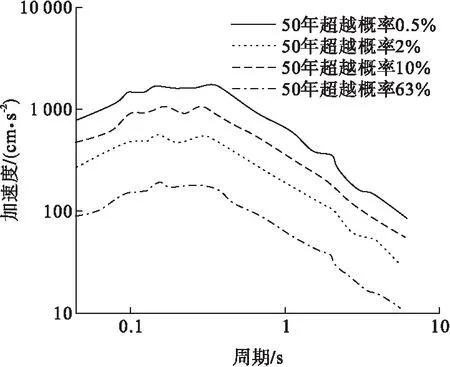
图1 50年不同超越概率加速度反应谱曲线

2 基于平动分量的水磨镇地区地震动场模拟

笔者采用随机有限断层法进行地震动场的模拟,随机有限断层法是将整个发震断层按照固定的规则分解成一定数量的子断层,由于划分后子断层尺寸较小,每一个子断层在计算中都可以视为一个点源模型[5]。通过对水磨镇区域划分网格,并针对各网格点采用上述有限断层法进行水磨镇地震动场模拟。

2.1 随机有限断层法震源参数确定

破裂面积和地震矩之间的关系为

logM0=1.5logS+logΔσ+logC.

(12)

式中:M0为地震矩;S为断层破裂面积;Δσ为应力降;C为常数,可按下式取值:

(13)

式中:L为断层长度;W为断层宽度;λ为拉梅常数;μ为剪切模量。

地震矩和矩阵级之间的关系为

logM0=1.5MW+16.1.

(14)

式中:MW为矩阵级。

应力降为

(15)

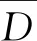
Δσ可按经验取值或者对实测地震数据的反演得到。文中取Δσ=4.0×106Pa。

(16)

圆盘断层的半径长度可以表示为

(17)

模拟地震动采用随机有限断层法时,其中的应力降参数的取值没有具体的规定,可以不通过计算而直接采用经验值或者对地震的反演得到的应力降参数。当震级大于5.5时,取平均值为4.0×106Pa。

对于长方形断层长度L:

(18)

(19)

断层长度和震级M的关系为

logL=-1.5+0.5M.

(20)

断层面积与震级的关系为

logS=-3.49+0.91M.

(21)

子源断层长度ΔL和子震震级MZ之间的关系:

log(ΔL)=0.4MZ-2.

(22)

在震级和破裂长度已知的情况下,与选定的子震震级相对应的子源平均破裂长度可以用式(23)决定:

log(ΔL)=logL-0.5(M-MZ).

(23)

对发震断层进行划分后,先确定子源地震矩,之后可以确定子震的个数:

Me=Δσ×A×ΔL.

(24)

式中:A为子源的面积。

子震的数量可以由式(25)表示:

(25)

综合考虑各子源产生的地震动到达目标场地的时间滞后效应,将每个子源产生的地震动加速度时程进行叠加,就可以得到断层破裂在目标场地引起的地震动加速度时程a(t):

(26)

式中:NL和Nw表示长度和宽度方向上的子断层数,NL×Nw=N即子源的总数;Δtij为可考虑断层破裂传播到第ij个子源引起的时间滞后效应和从第ij个子源至目标场地距离所引起时间滞后效应;aij(t)为第ij个子源引起的观测点的地震动。

高频衰减因子(k0)是采用有限断层法地震动模拟时考虑地形、地质条件影响的重要参数,对地震动峰值加速度影响较大,傅磊等[12]在采用该方法模拟两个不同台站的地震动时发现,k0的取值仅相差1.4%的情况下导致两个台站的PGA值相差近两倍。因此,笔者按式(27)考虑水磨镇地区各网格点的高频影响因子k0与高程之间的影响关系:

lnk0=-0.786-0.379×lnh.

(27)

式中:k0为目标场地各网格点处高频衰减系数;h为目标场地内网格点的高程。

2.2 基于地震动平动分量地震动场模拟

汶川地震发生后,很多学者对汶川地震发生的震源和断层模型进行反演,得到了该次地震的相关断层和震源参数[13-14]。笔者根据汶川地震实测数据,结合文献[5]中推演分析得到的震源参数结合有限断层法用于水磨镇地区地震动场模拟,相关震源参数取值见表2。

表2 汶川地震震源、传播路径和场地效应参数取值

图2和图3分别给出了模拟得到的水磨镇地区加速度反映谱和基于地震动平动分量的地震动场模型。由图2可以看出,模拟得到的水磨镇地区地震动加速度反应谱与基于历史地震数据危险性分析所得到的反应谱基本吻合,由于地震危险性分析时所选台站所处范围较广,有个别台站处于水磨镇区域范围以外的相近区域,导致地震危险性分析得到的加速度反应谱偏于保守,可能会低估水磨镇地区的地震风险。由图3可以看出,水磨镇地区西北角区域PGA值较大,自西北角向东南角呈递减趋势,东南角区域PGA值较小。

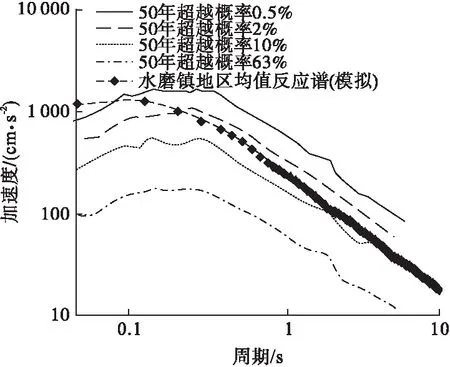
图2 加速度反应谱曲线

图3 基于地震动平动分量地震动场

3 基于地震动扭转分量的水磨镇地区地震动场模拟

已有研究表明[15-16],地震动并不是仅具有简单三个方向的平动分量,在平动分量的基础上还存在三个方向的扭转分量,包括两个绕水平轴的摇摆分量和一个绕竖轴的扭转分量。目前,关于地震动场模型的研究一般仅考虑地震动平动分量的影响,考虑地震动扭转分量的研究尚不多见。基于此,笔者在考虑地震动平动分量的基础上,进一步模拟得到基于地震动扭转分量的地震动场模型。

3.1 地震动扭转分量

3.1.1 Rayleigh波

在弹性介质中选择一立方体体积元,在坐标平面内投影(见图4)。在外力的作用下同时发生平动和转动,按图示几何关系即可得到立方体体积元形变前后对角线之间的夹角,即所产生的角位移:

图4 体积元形变原理示意图

(28)

由于体积元的变形极其微小,转角的正切值可以近似等于转角,即:

(29)

同理,另外两个坐标平面内角位移:

(30)

(31)

设势函数:

zexpi(ax-ωt).

(32)

zexpi(ax-ωt).

(33)

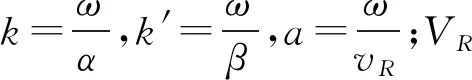
X向位移和Z向位移W可分别表示为

(34)

(35)

利用自由表面剪应力为零的边界条件可得到Raylay波绕Y轴的地震动扭转分量:

(36)

3.1.2 Love波

设第一土层和第二土层中波函数为

v1(x,z,t)=[Acos(pz)+Bsin(pz)]×

ei(ax-ωt).

(37)

v2(x,z,t)=Ce-bzei(ax-ωt).

(38)

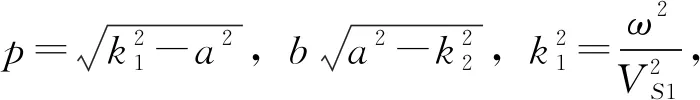
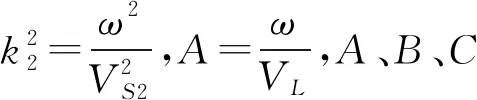
Love波只会产生竖向位移,即u=ω=0,所以扭转分量为

(39)

式中:v为y方向位移;VL为L波相速度。

若想要获得平面内以及出平面的地震动分量需要对获得的地震动平动记录进行分解,分解过程如下所示:

u=Tu′.

(40)

式中:u为分解得到的三个地震动水平分量和三个地震动扭转分量;u′为由地震台站实际得到的地震动三个水平分量地震动记录,坐标变换矩阵如下所示:

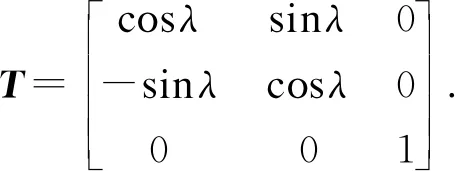
(41)

3.2 基于地震动扭转分量的地震动场模拟

基于以上方法得到水磨镇区域各网点的地震动扭转分量,进而得到基于地震动扭转分量的水磨镇地震动场(见图5)。可以看出,水磨镇区域地震动扭转分量峰值分布与地震动平动分量的峰值分布不尽相同,较大的地震动扭转分量有可能出现在地震动平动分量较小的网格点上,因此地震动扭转分量的影响也不容忽视。

图5 基于地震动扭转分量的地震动场

4 结 论

(1)通过地震危险性分析得到了该地区50年超越概率63%的地震烈度为6.3度,PGA=60 cm/s2;超越概率10%的地震烈度为8.0度,PGA=205 cm/s2;超越概率2%的地震烈度为9.1度,PGA=361 cm/s2;笔者特别考虑了巨震的影响,得到了50年超越概率0.5%的地震烈度为9.7度,PGA=593 cm/s2。

(2)通过模拟得到的水磨镇地区地震动场模型可以看出,地震动加速度峰值普遍较大、衰减较快,且自西向东,加速度峰值逐步递减,主要是由于山区地形地质条件造成的。

(3)通过建立基于地震动扭转分量的地震动场可以看出,在整个区域内扭转分量的大小分布情况与平动分量不一致,在某些平动分量较小的区域扭转分量可能会较大。因此,需关注地震动平动分量和扭转分量对村镇建筑的综合影响。