二级市场股票价格影响因素辨析——基于R 的多元线性回归

谢淳钰 万文君(通讯作者)

(武汉工程大学管理学院 湖北武汉 430205)

多元回归分析方法应用于股票定价逻辑剖析的思路，源于传统定价理论中的多因素定价模型，该模型在发展过程中多是基于实证观点建立起来的。

实证分析研究经济状态“是什么”，它侧重研究经济系统如何运作，分析经济活动的过程、结果和发展方向。实证分析在一定的假定条件下，描述、解释或说明已观察到的事实，对将会出现的情况或现象进行预测。客观事实是检验由实证分析方法得出结论的唯一标准。

有学者指出，实证分析的基本特征：以对经济现象分析归纳出的基本前提假设为起点，并基于这些假设进行逻辑演绎，推导出一系列结论，再逐步放松一些假设，使结论更接近具体事实。

1 研究方法

1.1 从企业价值研究开始

上市公司的整体价值由其股权资本价值和债务价值两部分组成。为了方便，我们将占比较小的优先股暂时忽略，以普通股价值作为企业资本的衡量标准；债务违约风险一般较小，其市场价格的变动也不会很大。由此，在企业资本结构不变的前提下，企业的整体价值越大，其股权资本的价值就越高，股票价格也就越高。

一般投资者都认可股价是由企业的内在价值决定的，但“内在价值”是财报中的哪些指标及怎样的权重决定的？如果这种定价逻辑在二级市场的行业板块中是普遍适用的，那么我们可以用截面数据拟合出定价的回归方程，从而揭示二级市场行业板块的定价逻辑。

1.2 多元线性回归模型

多元线性回归模型(multivariable linear regression model)中，当预测对象同时受到多个解释变量，，…，影响，且各个解释变量都与预测对象有线性相关时，可以建立多元线性回归模型进行预测和分析，模型为：

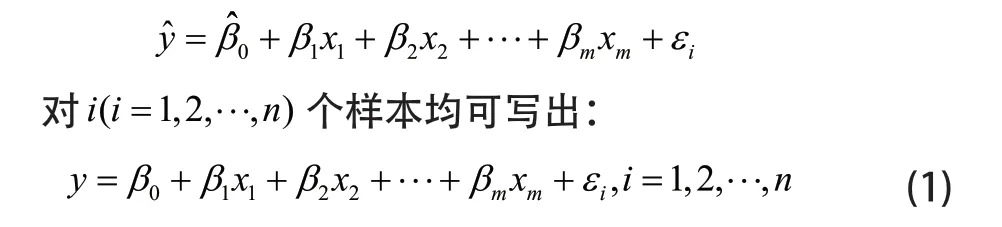
其中：为解释变量的数目；为回归系数(regression coefficient)；为随机干扰误差。式(1)也被称为总体回归函数的随机表达式。

由公式可以看出，解释变量有多个，我们构造模型时，应选取对被解释变量影响较大的几个解释变量，并且确定对应系数，再判断模型能否较好地拟合实测数据，才能进一步通过模型来预测。

在使用多元线性回归模型时，有四个基本假定：

假设一：各解释变量之间互不相关。

假设二：随机误差项是一个平均值或期望值为零的随机变量。

假设三：解释变量与随机干扰项不相关。

假设四：随机干扰项满足正态分布。

1.3 使用多元线性回归模型的前提条件

首先，行业板块概念清晰，定价逻辑成熟，即全新的概念板块可能定价逻辑尚在磨合中，对当前的股价没有指导意义。

其次，被评估企业所处的资本市场应有效或接近有效，上市公司在同等条件下相较非上市企业在接受资本市场评估时更易于获得有效价格。

再次，企业不能过于特殊，同一行业中寡头企业也许在收入模式上与其他企业有明显差距，所以应该尽量避免寡头垄断企业数据对行业板块数据的影响。

最后，多元线性回归模型要求解释变量之间互不相关，即不存在多重共线性。

1.4 数据来源和指标选择

数据来源为同花顺股票交易软件中的财报数据，易查找、更官方；截面数据时间选为2021年3月31日，股价选择20日均价；行业板块选为可降解塑料；指标选择综合考虑盈利能力、偿债能力、营运能力和增长能力等。

表1所列财务指标都是经过理论和实践长期检验的，因此首选将其列为备选指标。

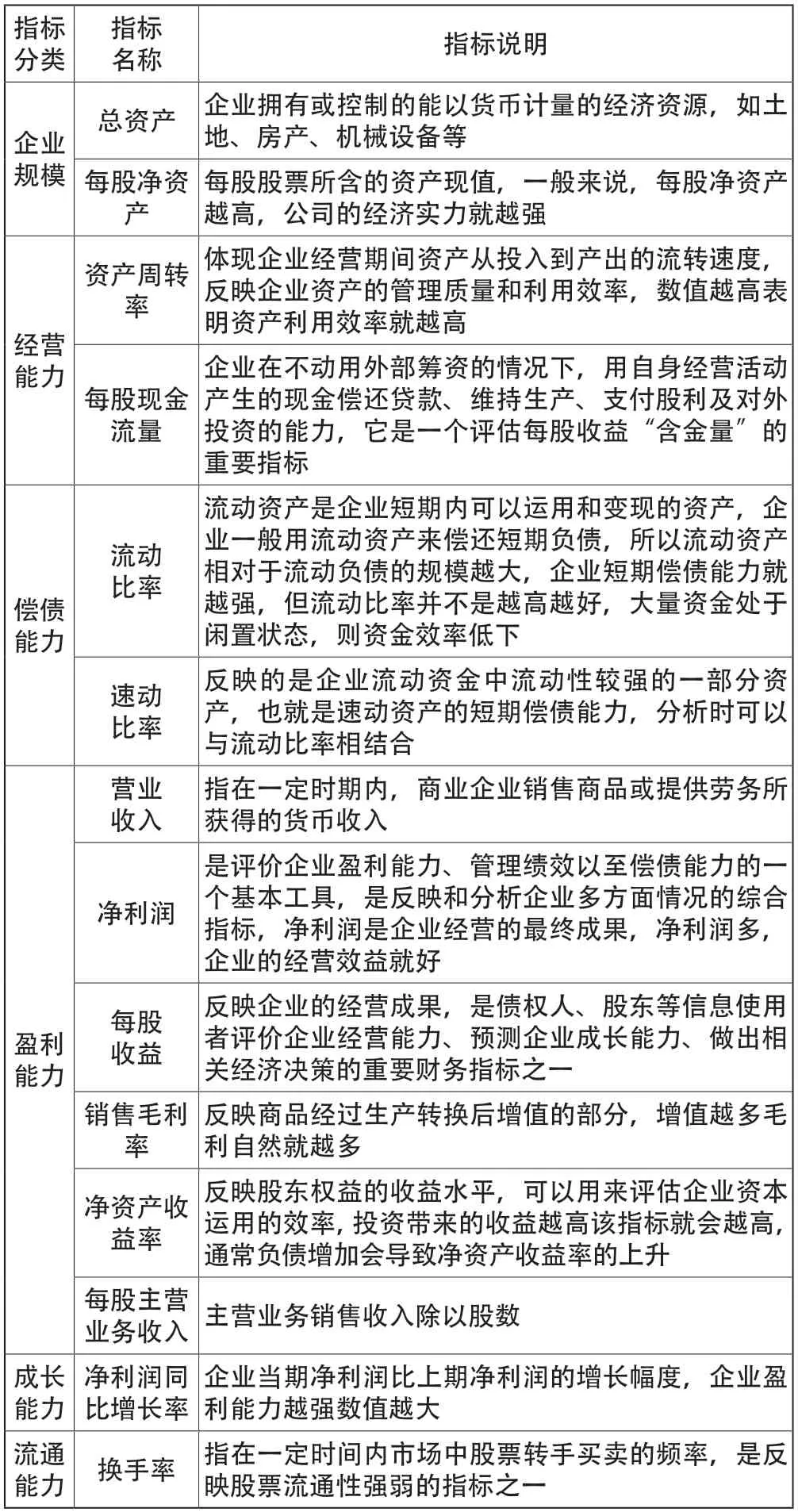
表1 备选解释变量一览

2 实例分析

2.1 建立多元线性回归模型

2.1.1 绘制散点图矩阵

散点图矩阵如图1所示。

图1 散点图矩阵

2.1.2 拟合多元线性回归方程

以前述股票数据中的“股价”为因变量，拟合各财务指标的多元线性回归方程，运行R语言summary()函数返回的信息如下：

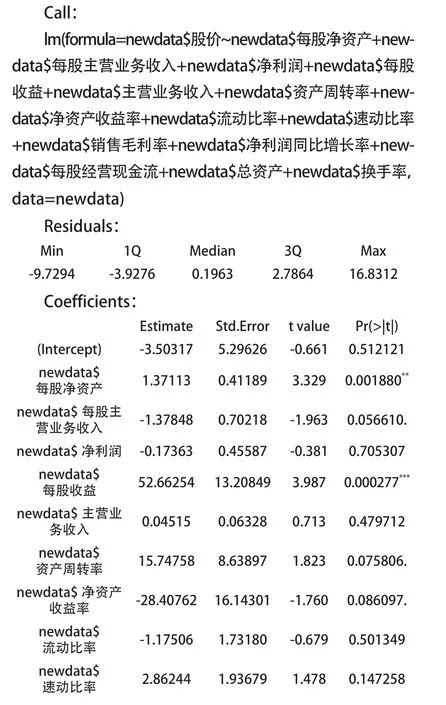
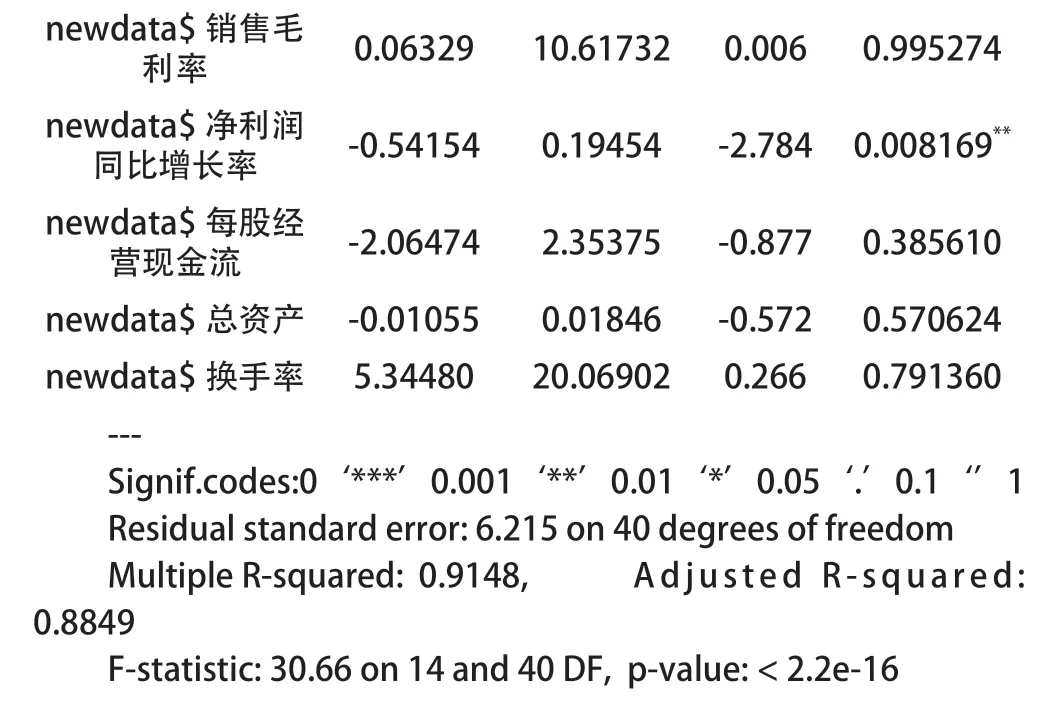
从回归参数的显著性可以看到：每股净资产、每股收益、净利润同比增长率通过t检验，拟合优度值达0.8849，多元线性回归方程整体通过F检验。

2.2 优化多元线性回归方程

以通过t检验的回归参数每股净资产、每股收益、净利润同比增长率，重新优化拟合回归方程，运行R语言summary()函数返回的信息如下：

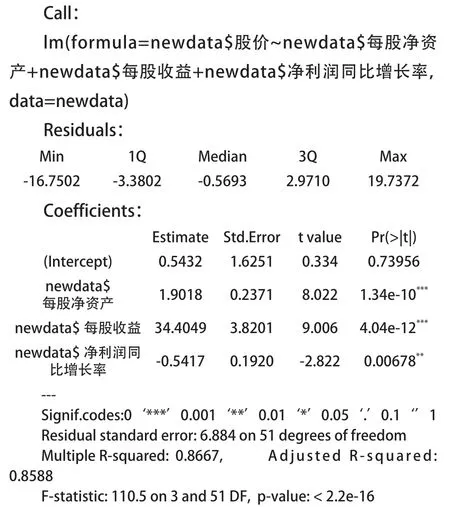
各自变量的p值为0.05水平上显著不为零，通过显著性检验；多元线性方程的拟合优度达到0.8588，通过F检验。

2.3 异方差检验

运行R语言bptest()函数，返回的信息如下：

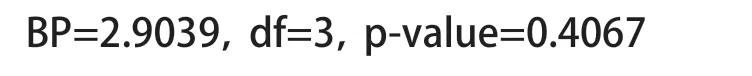
通过异方差检验。

2.4 自相关检验

由于此次回归分析中各自变量的数值为各股的财务指标，数值之间没有时间顺序上的相关性，因此自相关性检验在本例中没有意义。

2.5 多重共线性检验

运行R语言vif()函数，返回信息如下：

各回归参数的vif值均小于10，通过多重共线性检验。

2.6 建立多元线性回归方程

我们获得了关于股价的多元线性回归方程：

股价=0.5432+1.9018每股净资产+34.4049每股收益-0.5417净利润同比增长率

2.7 用回归方程计算拟合值

运用关于股价的多元线性回归方程，可计算得到个股的拟合价格，用拟合价格减实际价格的偏差计算偏差率，其偏差率数列的描述统计如表2所示。

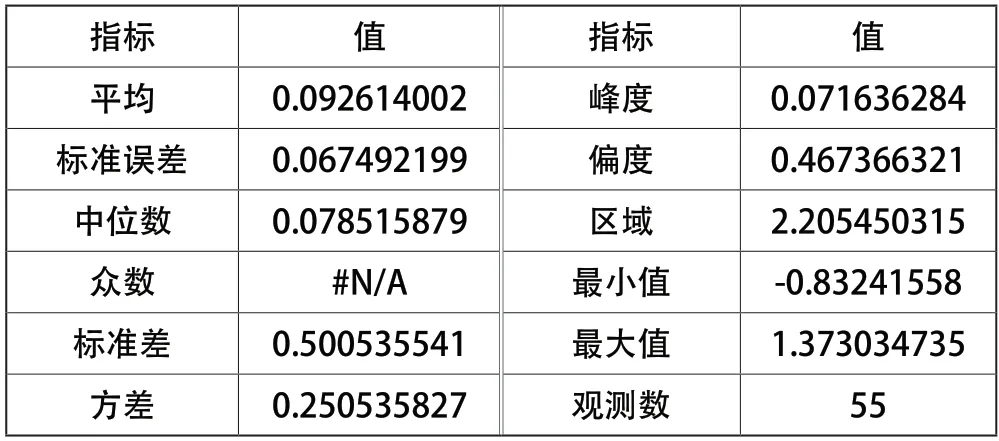
表2 个股拟合价格偏差率数列的描述统计

由表2可以看出，有少数股票的拟合股价正向偏差过大，牵动行业板块整体拟合股价正向偏移。

2.8 分析拟合股价的决策价值

我们以拟合股价正向偏差大于90%的4只个股(苏美达、紫江企业、湖北宜化、双星新材)为例，观察2021年3月31日—2021年11月30日的股价波动，发现各股20日均价的最大涨幅依次为33.95%、110.70%、685.95%、152.08%，而同期可降解塑料指数(代码885901)的最大涨幅仅为56.13%。

由此发现，拟合股价正向偏差较大的个股(实际股价远不及按行业定价逻辑拟合的股价)均在此后约半年的时间中有强于板块的补涨冲劲。

3 多元线性回归分析的特点

3.1 优点

3.1.1 降低了研究者的进入门槛

与通过财务报表对股价进行分析相比，数理统计分析方法无需分析人员深刻把握宏观经济、产业发展趋势、市场竞争条件、企业经营状况等，仅需掌握数理统计分析技术和初步的财务知识即可。

3.1.2 有效防范研究者的主观臆断

多元线性回归分析仅依据行业和个股财报数据作出分析结果，排除了分析人员的主观因素，也可以降低因分析人员经验不足导致的分析偏差。

3.2 缺点

3.2.1 需要数据量庞大

在数据量较少时，回归分析更容易得到显著结论。一般认为，样本数量大于30时，分析结论才更有保障，同时因为要在众多的自变量中筛选具有显著性的自变量，所以有大量的数据收集和整理工作。

3.2.2 忽略了非上市公司在行业中的影响

此次行业股价回归分析中，由于非上市企业的财报不公开披露，同时非上市企业才是行业市场中的多数，所以抽样范围受限造成结论偏差在所难免，但没有影响我们探索市场定价的基本逻辑。

4 结语

相较传统的企业价值评估，数理统计分析的特点在于客观性、时效性、普遍性，只要有足够的数据，就可以充分揭示复杂经济现象下深刻的内在规律。

此次对可降解塑料行业二级市场定价影响因素的辨析，我们发现：多元线性回归分析对于行业板块股价的定价机制揭示准确、可靠，可以作为一种投资参考工具。

随着市场周期性的波动，在市场不同趋势阶段，二级市场股票定价的影响因素是否保持稳定？会不会在市场盘整趋势和下降趋势中显现出其他影响因素的显著作用？值得我们进一步研究和揭示。