多文字可满足SAT问题的相变点上界*

芦 磊,王晓峰,2,梁 晨,张九龙

(1.北方民族大学计算机科学与工程学院，宁夏 银川 750021； 2.北方民族大学图像图形智能处理国家民委重点实验室，宁夏 银川 750021)

1 引言

可满足性SAT(SATisfiability)问题是一种特殊的约束满足问题 CSP(Constraint Satisfaction Problem)，也是最基本的CSP问题。给定一个合取范式CNF(Conjunctive Normal Form)公式F，SAT问题指是否存在一组布尔变元赋值，使得F中每个子句至少有1个文字为真。在SAT问题中，子句长度为k的SAT问题被称为k-SAT问题。k≥3的k-SAT问题是世界上第一个被证明的NP-完全问题[1]。

本文研究的多文字可满足SAT问题MLSAT(Multi Literal SATisfiability problem)是指：是否存在一组变元指派，使得SAT实例的每个子句至少有2个文字为真。显然，MLSAT问题仍然是NP难问题。MLSAT问题是SAT问题的特殊情况，如果一个赋值指派是MLSAT问题的解，则其必然也是SAT问题的解。在现实生活中，MLSAT问题也很常见，如机器调度问题往往需要多台机器同时运行，又比如在竞赛中，往往需要3局2胜才能取得胜利。各种NP难问题往往不会恰好编码为严格的SAT问题，因此，研究多个文字为真的SAT问题很有意义。

设F是MLSAT问题中n个布尔变量x1,…,xn的随机3-CNF公式，m为F的子句个数，约束密度α=m/n。本文研究的问题是计算最小实数α*，当n趋于无穷大时，如果α严格大于α*，3-MLSAT问题可满足的概率收敛到0。在这种情况下，3-MLSAT问题高概率不可满足。实验数据表明，α*的值在0.65左右。实验还表明，如果α严格小于α*， 3-MLSAT问题高概率是渐近可满足的。因此，从实验上讲，α*既是可满足性相变点上界，又是命题公式由可满足变化到不可满足的阈值。本文模型从3-CNF公式出发，可推广到k-CNF公式。通过对相变上界的研究，不仅有助于进一步认识这类问题的难解本质，还有助于设计出更为高效的算法。

MLSAT问题是SAT问题的衍生问题，研究SAT问题的相变点上界，对研究MLSAT问题很有参考意义。在多项式时间内，任意CNF公式都可归约转换到3-CNF公式[2,3]，因此，学术界普遍研究3-SAT问题的相变点上界。1983年，Franco等人[4]利用一阶矩方法的简单应用产生了5.191的上界。1992年，文献[5]经过实验验证存在相变点。在后续的研究中，文献[6]是一个重要的进步，Kamath等人基于占用问题和独立变量，将上界提升到了4.758。文献[7]基于一阶矩负素解，将上界提升到4.64。文献[8]基于一阶矩随机变量序列，将上界提升到4.667。文献[9]通过限制典型句法特征，又迈进了一大步，将上界提升到4.506。在此基础上，Dubois等人[10,11]对相变点上界进行了综述。文献[12]将上界提升到了4.489 8，这是目前为止最好的上界。此外，基于统计物理的理论性但不严谨的工作研究[13,14]，阈值估计在4.27左右。

本文针对MLSAT问题的相变点上界展开研究，引入随机CNF实例产生模型，利用一阶矩和文献[8]中的局部最大值技术，提升了该问题的相变点上界。具体地讲，利用简单的一阶矩证明，当k=3时，α*=1(具体请参考定理1)；利用单次翻转，α*提升到了0.740 4(具体请参考定理2和定理3)；利用2次翻转，α*提升到了0.719 3(具体请参考定理4)，本文的模型可推广到k-CNF公式。最后，选择变元规模为100和200的随机CNF实例进行实验，验证了k=3和k=4时的2种情形，实验结果均表明：理论结果与实验结果相吻合。为了方便描述，本文所有的“满足”均默认为MLSAT问题。

2 基础知识

2.1 MLSAT问题实例生成模型

2.2 一阶矩简单证明

定理13-MLSAT问题的不满足阈值α*=1,4-MLSAT问题的不满足阈值α*=1.8499，k-MLSAT问题的不满足阈值为α*=-ln 2/ln(1-(k+1)/2k)。

在证明定理1之前，需要先证明引理1。

引理1在MLSAT问题中，对于任意指派Z={z1,z2,…,zn}∈{0,1}n，指派Z可满足的公式数量是相同的。

□

下面再证明定理1：

(1)

□

3 主要结论

3.1 单次翻转证明相变点上界

(1/2)α(2-e-3α/2)=1

(2)

在证明定理2之前，需要先证明下面几个引理。

证明在3-MLSAT问题中，给定3个不同的变量xi,xj和xk，其文字组合有8种。对于任意一个文字组合，可满足的赋值指派有4种，设恰好满足该子句2个文字的真值指派为A1，更改A1的变元取值，更改后的指派不满足该子句。从一个子句出发，可推导至m个子句，引理2得证。

□

(3)

其中,

(4)

引理3得证。

□

A∈Sn]

(5)

□

下面给出定理2的证明：

(6)

□

(7)

(8)

定理3得证。当k=4时，α*=1.6085，符合第3节的实验结果。

□

3.2 2次翻转证明相变点上界

引进变量字典序的定义：变量赋值为False的字典序小于赋值为True的。定义字典序的作用是识别关于n个变量的赋值指派的类别。2次翻转也从3-CNF公式入手。

引理5在MLSAT中，式(9)中的马尔可夫不等式成立:

(9)

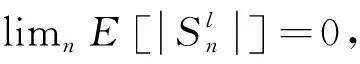
引理6式(10)成立：

(10)

3.2.1 概率计算

先来介绍一下子句的生成模型:

Gp：模型中的每个子句都以独立的概率p出现在公式中。

Gm：通过均匀且独立地选择m个子句且不放回抽样来获得随机公式。

Gmm：通过均匀且独立地选择m个子句且放回抽样来获得随机公式，本文中使用的即为Gmm模型(请注意，我们仅引用赋值指派A满足的子句)。

(11)

(12)

引理7式(13)成立：

(13)

(14)

引理7得证。

□

Janson不等式

(15)

□

利用Janson不等式的上述变体得出如式(16)所示结论:

(16)

根据引理7，ε=o(1)。现在计算不等式中出现的Δ，设置u=e-3α/2，则式(14)变为如式(17)所示：

(17)

引理8令df0和df1为2个2次翻转，它们共享从False变为True的变量。然后可以得到式(18)：

(18)

□

引理9令df0和df1为2个2次翻转，它们共享从True变为False的变量。然后可以得到式(19)：

(19)

□

现在，观察到2次翻转的有序对的数量最多为df(A)·n，且引理8中的概率小于引理9中的概率。代入Δ，得到式(20)：

(20)

将式(17)和Δ代入式(16)，得到式(21)：

(21)

在u的取值范围内，不等式的右侧表达式最多为1。现在，通过式(10)～式(12)和式(21)，得到式(22):

(22)

其中：

X=1-u+o(1)

(23)

(24)

在3.3.2节中，将给出不等式(22)总和的估计值。

3.2.2 数值估计

引理10如果0≤X2≤Y≤1，则式(25)成立:

(25)

其中：

证明原理请参阅文献[26]，然后对n进行归纳[27,28]。

(26)

(27)

最后，令df_eq(α)是在公式ln(1/2)α(Z′/2)+dilog(1+X)-dilog(1+XeZ′/2)中替换X和Z′的值且去掉它们的渐近项时得到的表达式。引理10得证。

□

使用Yn/2=eZ′/2和Y=1+o(1)，则可以得到df_eq(α)的表达式如式(28)所示：

df_eq(α)=ln(1/2)α(Z′/2)+

dilog(Z′/2)-dilog(1+XeZ′/2)

(28)

方程df_eq(r)=0的唯一正数解即为α*。使用Matlab 获得了值α*=0.7193，定理4得证。

□

4 数值实验与分析

在实验中，利用第1节中的MLSAT问题实例模型G(n,k,α)来生成随机实例，取2组变元规模不同的数据，规模分别为n=100和n=200。根据定理1,当k=3时，α*=1；当k=4时，α*=1.8499；根据定理2和定理3，当k=3时,α*=0.7404；当k=4时,α*=1.6085。根据定理4，当k=3时,α*=0.7193。图1和图2分别表示k=3和k=4时的MLSAT问题的相变现象，图中的每个数据点均由100个随机实例的统计结果产生，横坐标表示相变控制参数α，纵坐标表示MLSAT问题实例可满足的统计概率。经实验得到，3-MLSAT的相变点在0.6～0.8，4-MLSAT的相变点在1.4～1.8。本文理论结果与实验结果吻合。

Figure 1 Phase transition phenomenon of MLSAT problem (k=3)图1 MLSAT 问题的相变现象 (k=3)

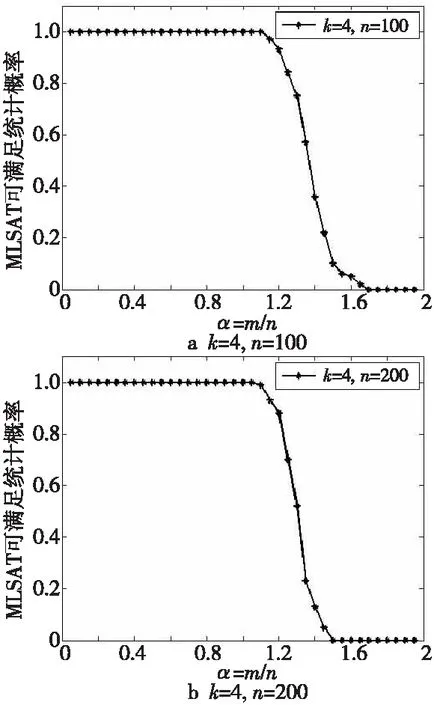
Figure 2 Phase transition phenomenon of MLSAT problem (k=4)图2 MLSAT 问题的相变现象 (k=4)

5 结束语

本文分析了随机多文字可满足SAT问题的可满足性相变点上界。具体地讲，设α*是关于k(k>3)的一个常数，F是一个随机CNF实例，当相变控制参数α>α*时，则F是高概率不可满足的。多文字可满足SAT问题可以看作是SAT问题的一种特殊情况，对该问题相变现象的分析，有助于分析SAT问题及其同类型问题的相变。在研究中使用了一阶矩和局部最大值方法，通过构造实例的解结构，给出了相关结论。下一步将利用更精确的方法研究相变上界，研究多文字可满足SAT问题的相变下界等。