基于车底使用数量最少的动车组运用计划优化研究

陈旻瑜，张雨洁，张守帅，闫海峰

（1.山东省铁路投资控股集团有限公司 运营管理部，山东 济南 250102；2.西南交通大学 交通运输与物流学院，四川 成都 611756)

0 引言

截至2021 年底，我国铁路营业里程已达15 万km，其中高速铁路营业里程达4 万km。随着我国高速铁路路网规模的进一步扩大，动车组作为高速铁路系统中实现运营任务的关键载体设备，其需求量不断增加。目前动车组运用计划通常由动车调度员根据中国国家铁路集团有限公司下发的运行图，再结合不同等级维修要求的约束条件，进行人工编制[1]。当前我国正在大力推广根据旅客需求动态调整的高速铁路“一日一图”运营模式，且已在京张高速铁路实现[2-3]，而既有人工编制动车组运用计划的方法很难适用于复杂多变的运营情况，导致动车组运用计划质量和效率难以满足现有需求，因此有必要对动车组运用计划进行优化研究。

既有研究中，针对动车组运用计划优化模型的构造方法可汇总成2 类：一类是基于列车运行图或动车组交路图直接构建整数规划模型[4-6]，另一类是将其抽象成其他数学问题如指派问题[7]、旅行商问题[8]等，或借助接续网络[9]间接构造。在求解方面，大多数文献以智能算法为主，如粒子群算法[10]、模拟退火算法[4]等，也有少部分文献采用商业求解器[11]求解。

综上，在列车运行图给定的基础上，结合当前高速铁路运输组织模式、一级检修里程约束、动车组配属情况以及动车组运用方式等对动车组使用效率和数量产生影响的因素，对动车组运用计划进行优化研究。对于运行线间接续关系多且复杂的情况，提出将其抽象成连续型时空网络的方法，以更加清晰直观地描述动车组运用情况。在模型建立时引用0-1 变量表述动车组车底是否使用和分配任务情况，将非线性约束条件进行线性化处理，并直接采用商业求解器求解。对于求解时间长的问题，提出将动车组集合拆分为必用和备用2 部分以减少求解规模，降低求解难度，从而实现快速高效的对动车组运用检修计划整体优化。

1 时空网络模型构建

1.1 问题描述

对于编制动车组运用计划的问题，最重要的就是解决2 个子问题：①给每条运行线分配合适的动车组承担运输任务；②安排即将满足检修周期条件的动车组回到相应所属动车段(所)内完成检修任务。动车组在实际运用检修过程中的位置及运用状态变化，可以抽象成时空网络中的节点，以及由任务节点组成的弧段。在设计的连续型时空网络中，时间轴限度即为计划编制周期，空间轴限度即为归属本段动车组能到达的最远车站。每一列动车组均有多条路径可以选择，每条路径都会通过任务节点及弧段的坐标详细表明作业状态及时空信息。结合动车组交路编制计划中需满足的优化目标和约束限制，形成在编制周期内每列动车组最终的路径组成方案。

1.2 时空网络的基本元素组成

基于给定的列车运行图，构建动车组时空网络G{V，A}。其中，V表示时空网络中的节点集合，具体包括出入段作业节点、运用作业节点、检修作业节点；A表示时空网络中的弧段集合，具体包括运输作业弧、检修作业弧、出入段弧、列车接续弧。用各节点和弧的坐标值描述当前所处状态的时间和空间。在纵坐标设计时，把含动车段(所)的车站进行分割，分割为进行接发车作业的车站和可进行检修作业任务的动车段(所) 2 部分。时空网络元素的构建如下。

（1）任务节点。

①出入段任务节点。出入段任务节点集合Vd由出段任务节点集合与入段任务节点集合两部分组成。定义动车段(所)集合为D={dk|k=1，2，…，m}，dk表示第k个动车段(所)，m表示动车段(所)的修建数量。定义动车组集合E={edl|d∈D；l=1，2，…，n}，edl表示动车段(所)d配属的第l列动车组，n表示该动车段(所)配属的动车组数量。当动车组edl从动车段(所)d出发时，记为出段任务节点，该节点的时空网络坐标表示为，即表示动车组edl的出段时间、表示动车组edl当前离开的动车段(所)位置。当动车组回到动车段(所)时，记为入段任务节点，同理该节点的时空属性记为进入动车段（所）时间及编号。

②运输任务节点。运输任务节点Vw由运输任务开始节点与运输任务结束节点两部分组成。定义需要完成的运输任务集合W={wi|i=1，2，…，j}，wi表示第i个运输任务，j代表运输任务数量。车站集合为U={uv|v=1，2，…，o}，uv表示第v个车站，o表示车站数量。对于每个运输任务，设置一个开始节点，该节点在时空网络中的位置对应该运输任务w开始时间及车站地点；设置一个结束节点，其所对应该运输任务的结束时间为，结束车站地点为。

③检修作业节点。检修作业节点Vx由检修作业开始节点与检修作业结束节点两部分组成。检修开始时间记为，检修结束时间记为；检修地点记为。

以上3 种任务节点的集合被记为V，因此存在V=Vd∪Vw∪Vx。

（2）作业弧段。

①运输作业弧Aw。将运输任务的出发节点与到达节点相连，即可得到运输作业弧其中Aw根据运输任务的上下行方向不同，又可分为上行运输作业弧和下行运输作业弧，定义运输任务弧段的权重为该运行任务的里程。

②检修作业弧Ax。将检修作业的开始节点与结束节点相连，即可得到检修作业弧定义检修任务弧段的权重为该检修任务的检修时长Tr。

③出入段弧Ad。对任意始发车站为动车段(所)的运行任务建立出段弧，表示某个动车组从动车段(所)出发即将上线担任运输任务。类似地，对任意终到动车段(所)的运输任务建立入段弧，表示某个动车组担当完某一运输任务后需进行检修作业或完成该运输任务后已到达全日运营结束时刻。定义出入段弧长权重为0。

④接续弧AC。用于连接上一运输任务的到达节点和下一运输任务的出发节点。接续条件是下一运输任务的开始时间与上一运输任务的到达时间之差需要满足最短接续时间约束。定义列车接续弧段的权重为该两运输任务间的接续时长。

以上4 种弧集合被记为A，因此存在A=Aw∪Ax∪Ad∪Ac。

时空网络模型示意图如图1 所示，图中包含3个车站，其中车站B 为动车段(所)连接的车站。用不同样式的点和箭头标明任务节点及有向弧段。

图1 时空网络模型示意图Fig.1 Schematic diagram of space-time network model

2 动车组运用计划优化模型构建

2.1 基本假设

动车组运用计划优化模型是在列车开行方案和运行图已知的基础上，假设不发生临时增减、改变运行图及列车晚点情况，且认为动车段(所)检修能力足够大。以完成运行图给定的运输任务为前提，考虑一级检修约束条件，针对单一编组形式的同一型号动车组，进行运用和检修计划优化，提高其使用效率。

2.2 符号定义

基于上述对时空网络模型与动车组运用计划相结合的分析，给出参数和变量符号的定义及说明。参数定义如表1 所示，变量定义如表2 所示。

表1 参数定义Tab.1 Parameters definitions

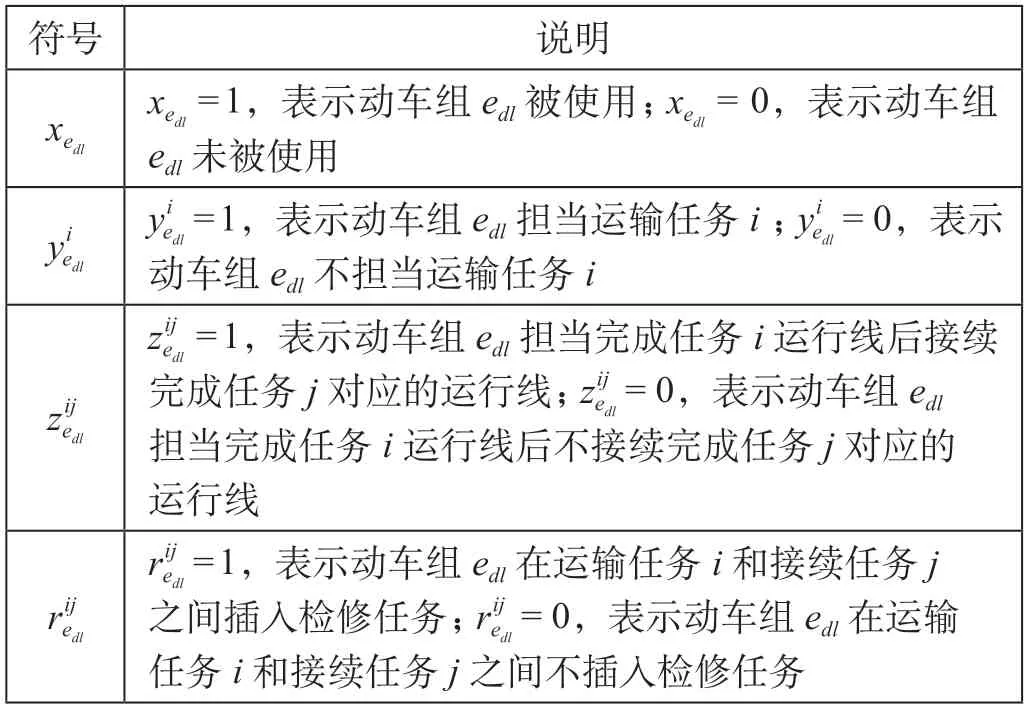
表2 变量定义Tab.2 Variable definitions

2.3 数学表达

2.3.1 优化目标

模型选取完成全部运输任务所需最少车底数Z为目标函数。

2.3.2 约束条件

（1）必用动车组约束。在模型中，为降低求解复杂度，将动车组集合拆分成必用动车组集合和备用动车组集合，设必用动车组集合为备用动车组集合为从而简化决策变量xedl未知个数。在实际中，各动车段(所)也可以根据经验大体确定至少必用动车组数量。所有必用动车组集合中的动车组值均为1。

（2）动车组使用情况与是否完成运输任务间约束。当动车组edl是被使用的动车组时，才有可能承担运输任务i，因此得到以下约束条件。

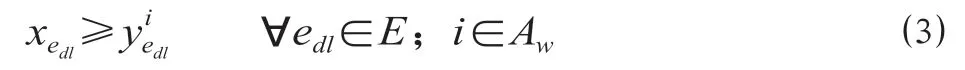
（3）动车组使用情况与是否完成接续间约束。即只有当动车组edl被使用时，才有可能在承担运行线i后接续运行任务j。

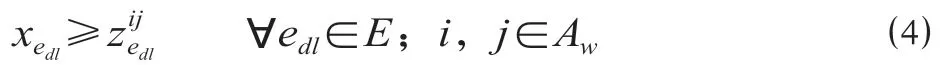
（4）完成当前任务和接续下一任务间约束。动车组edl在完成运行线i后接续运行线j(即=1)的前提条件是动车组edl既担当运行线i，又担当运行线j。

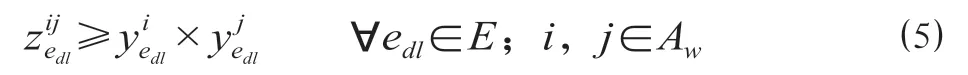
（5）一级检修里程约束。模型仅考虑动车组一级检修的运营里程约束。为避免超期检修所带来的安全隐患，当动车组运行累计一定里程后，将要对其进行一级检修。

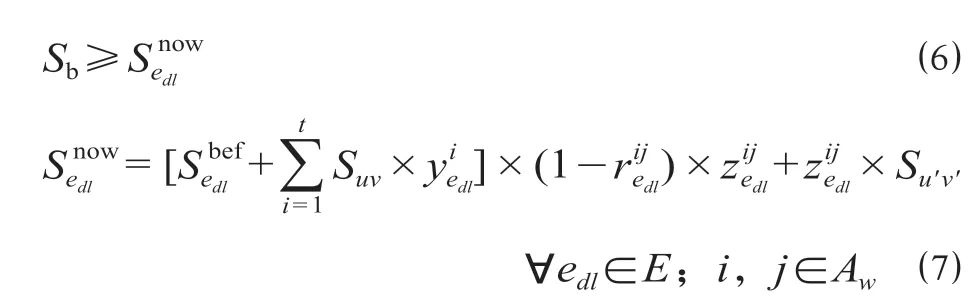
式中：Sb为一级检修里程约束，经查阅资料为5 000 km；Suv为对应已完成任务运行线i中所连接的2 个车站间距离；Su'v'为即将继续完成的运输任务j所对应的2 个车站间距离。

需要注意的是，如果进行检修，则在检修后应消除检修之前的累计里程值。

（6）动车组检修条件约束。

①是否进行检修作业与是否接续间约束。动车组edl是否在完成任务i后安排检修作业的前提，是该动车组必须要接续下一运输任务j。即取1的前提条件一定是=1。

②检修作业地点约束。当动车组edl的检修作业开始节点是其配属段时，方能进行检修。

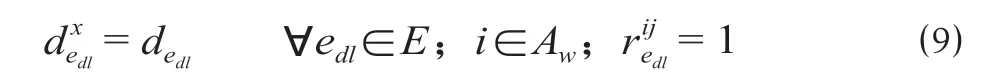
其中为动车组edl的所属动车段。

（7）运输任务全覆盖约束。每条运行线均应分配一列动车组以完成运输任务，且每列动车组在同一时段只能完成一个运输任务。

（8）接续时间约束。动车组接续时间应满足最小及最大的接续时间约束。最小接续时间应保证完成动车组的折返作业以及备品补充、车厢清洁等整备作业。当在两接续任务间加入检修作业时，还需预留出检修作业时间。此外，为了提高动车组运用效率，减少动车组运用数量和车站到发线占用时间，当一个动车组执行完一条运行线以后，不允许在车站到发线上停留过多时间，因而需要有最大接续时间的限制。

（9）接续任务约束。在接续选择判断时，需要检查上一运输任务的终到车站与下一运输任务始发车站是否为同一车站。

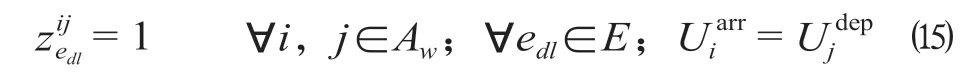
（10）决策变量域约束。

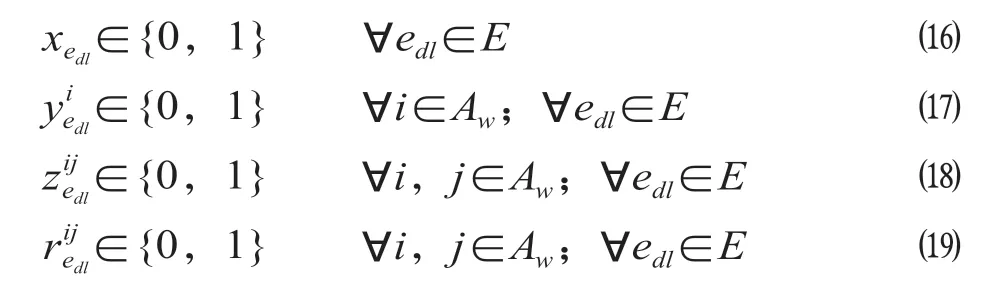
2.3.3 模型处理

将非线性化约束进行线性化处理，将约束 ⑷条件进行线性化处理，即把乘法关系转换成加法关系，以使用线性化求解软件处理。将转化为

2.3.4 求解步骤

根据列车运行图构建动车组运用计划的时空网络，初始化各节点弧段数据，在根据经验确定必用动车组使用数量基础上，对其调用CPLEX求解器求解。与其他纯线性问题相比，本模型属于0-1 整数规划问题，因此针对该问题求解器会采用分支切割算法，即将其划为一系列LP 子问题求解。

求解器求解步骤如下。

步骤1：根据历史数据和经验确定必用动车组数量，并根据线路情况、既定运行图和动车段位置初始化数据信息。

步骤2：在CPLEX 求解器中，定义变量、集合、索引、参数，并输入参数数据、求解时间范围，设置求解目标函数、约束条件等。

步骤3：调用CPLEX 求解器，其原理即为对原问题进行松弛，将整数问题转化为线性问题求解，若所求结果恰好是整数解，则直接跳到步骤5，否则对原问题进行分支处理。

步骤4：对每个分支的问题进行求解，并与其他分支的解相比较，将目标函数值最小者定成新下界；在已符合整数条件要求的分支中，找出目标函数值最小者作为新上界。如此反复进行分支定界步骤，过程中对结果不在上下限内的分支进行剪枝处理，直至求得最优解。

步骤5：输出最优解，求解结束。

3 算例分析

为验证模型可行性，选取国内某条线路2021年6 月的运行图作为算例，在此基础上编制动车组交路计划。动车组分配交路任务情况如图2 所示。算例中包含46 条运行线，途经2 个车站。假设动车组运用计划编制周期为1 d，各动车段根据运行图准备2 列必用动车组和5 列备用动车组。在参数方面，设置相邻运行线间最小接续时间为20 min，一级检修里程最大值为5 000 km，一级检修作业时间为240 min。求解采用CPLEX 求解器，求解环境为Intel(R) Xeon(R) CPU E5-2609 v2 @ 2.50 GHz，内存32GB，64 位操作系统的台式计算机。

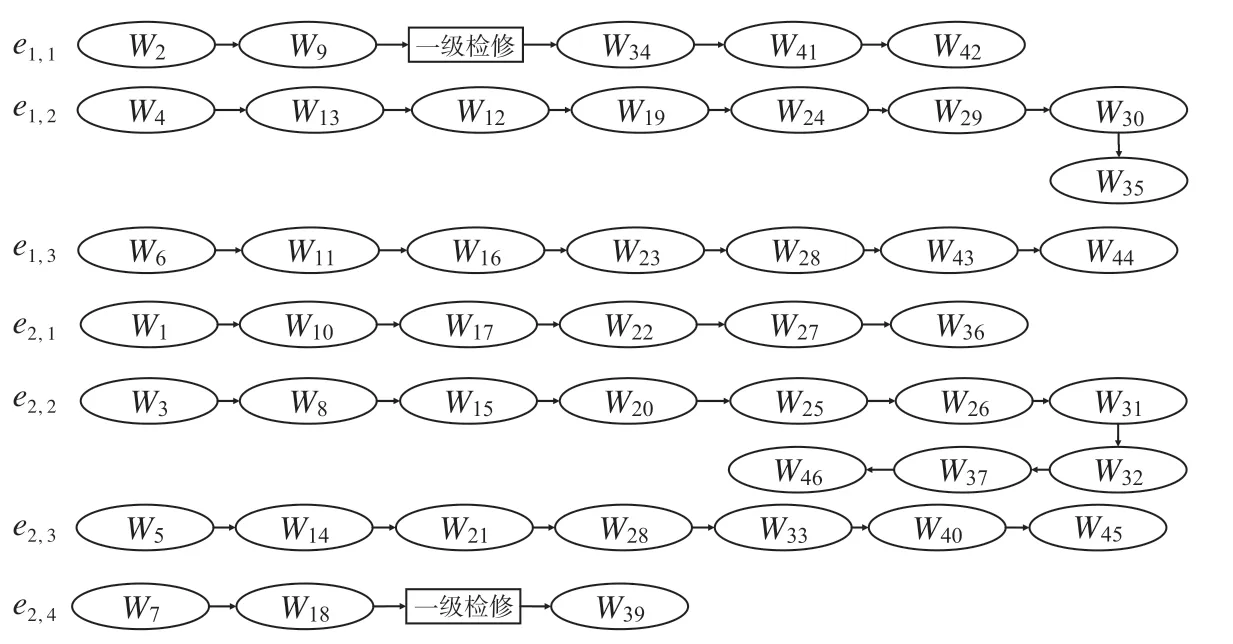
图2 动车组分配交路任务情况Fig.2 EMU assigned routing tasks

优化模型与人工编制方法比较结果如表3 所示。

表3 优化模型与人工编制方法比较结果Tab.3 Comparison table of results between the optimization model and manual method

由计算结果可知，优化模型与人工编制结果相比，动车组平均日车公里提高12.5%，减少动车组车底使用数量，增加企业经济效益。

4 结束语

通过构建0-1 整数规划模型对高速铁路动车组运用计划进行优化。在约束条件上，考虑了决策变量间的检修约束、唯一性约束、接续条件约束等相互关系约束；为进一步简化模型，降低求解难度，提出将动车组集合分为必用动车组集合和备用动车组集合，并对约束条件进行线性化处理，使改进后的模型能直接由商业软件求解。实例分析表明：动车组运用计划优化模型可以有效降低动车组使用数量，提高动车组平均日车公里。该研究是在同一车种、同一编组方式的条件下展开的，进一步将考虑动车段(所)检修能力、多车种情况以及站内进行重联摘解作业情况下的动车组运用计划编制优化问题。