西部陆海新通道成渝物流枢纽建设的竞合博弈策略研究

杨 波，陈园园

（重庆邮电大学 经济管理学院，重庆 400065)

0 引言

西部陆海新通道自2017 年4 月建设以来，成渝至北部湾港之间逐渐形成了重庆—贵州—南宁—北部湾港、重庆—怀化—柳州—北部湾港，以及成都—泸州—百色—北部湾港3 条东、中、西铁路运输通道，并实现常态化运行。相比经上海至东盟国家的水运线路，铁路运距缩短了约1 000 km，货运时间缩短了12 d，运输效率显著提升。2021 年，西部陆海新通道铁海联运班列累计开行6 117 列，共发送货物57 万TEU，不断提高了西部陆海新通道物流枢纽的经济效益。数据增长的背后，是西部陆海新通道建设带动形成的巨大市场，但成渝双方作为相邻城市存在争抢货源的现象[1]。以重庆为始发点的东、中线路运输效率较高，且随着重庆“一主两辅多节点”枢纽体系的快速形成，其运输需求规模逐年上升，市场发展潜力巨大。以成都为始发点的西线由于铁路设施建设滞后，占西部陆海新通道货物运输的市场份额较低。但随着成都区域内物流枢纽建设的逐渐完善，并不断打通西部地区通往北部湾港最近的出海货运通道，将会有效提升成都铁路运输的通行效率。成渝在物流枢纽运营上若展开激烈的竞争，不利于市场的有序发展和区域资源的合理流动，而且促进双方达成合作是实现西部陆海新通道成渝去回程班列运输平衡的重要举措。为了助力成渝在物流枢纽运营上建立良好的竞争与合作关系，促进西部陆海新通道可持续发展，有必要对双方的竞合关系进行研究[2]。

基于以上背景，以成渝在物流枢纽运营的竞合关系为入手点，构建双方静动态的竞合博弈模型；以此分析成渝竞合策略选择对双方物流枢纽运营收益的影响，进而研究双方竞合策略选择和演化趋势。

1 模型构建

1.1 静态竞合博弈模型构建

伯川德博弈理论假设博弈方均为完全理性人，以价格为决策变量构建收益函数。考虑到重庆与成都在物流枢纽建设运营上的实际情况，假设双方对于彼此之间的信息、资源及博弈策略并不是完全了解。另外，重庆和成都之间存在具有竞争关系的物流枢纽设施，并提供较强的同质性服务，则运输费用将会成为货主选择的重要因素。因此，基于伯川德博弈理论假设i和j作为2 个博弈方，分别表示重庆与成都的物流枢纽设施。为了争取区位优势与规模效应，在运营过程中服务价格成为成渝竞争以及影响双方物流枢纽设施的运输需求量的主要因素[3]，因此设博弈方重庆和成都物流枢纽设施的需求函数分别如下。

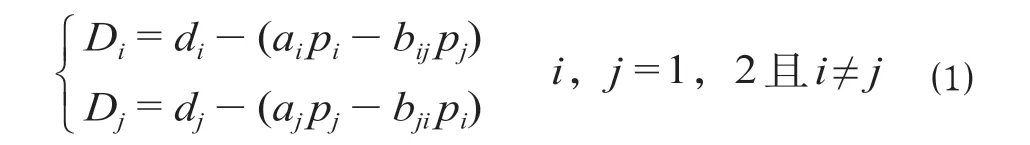
式中：Di为重庆物流枢纽设施的总运输需求量，TEU；Dj为成都物流枢纽设施的总运输需求量，TEU；di为不受价格因素影响时重庆物流枢纽设施能够获得的运输需求量，TEU；dj为不受价格因素影响时成都物流枢纽设施能够获得的运输需求量，TEU；pi为从重庆到北部湾港单个标箱的运输费用，元/TEU；pj为从成都到北部湾港单个标箱的运输费用，元/TEU；ai为重庆物流枢纽设施的运输价格变动导致自身需求量变动的影响系数；aj为成都物流枢纽设施的运输价格变动导致自身需求量变动的影响系数；bij为成都物流枢纽设施的运输价格变动导致重庆运输需求量波动的影响系数；bji为重庆物流枢纽设施的运输价格变动导致成都运输需求量波动的影响系数；其中ai，aj>0 且ai≠aj，bij，bji>0 且bij≠bji，即双方均不能提供完全替代的同类服务。

假设博弈方重庆和成都物流枢纽运营成本函数分别为

式中：Ci为重庆物流枢纽设施的总运营成本，元；Cj为成都物流枢纽设施的总运营成本，元；V为重庆与成都物流枢纽设施运营的单位边际成本，元/TEU；Fi为重庆物流枢纽设施运营的固定成本，元；Fj为成都物流枢纽设施运营的固定成本，元；在此设Fi和Fj等于零。

将需求函数代入成本函数，可得出博弈方重庆和成都的物流枢纽运营收益函数分别为

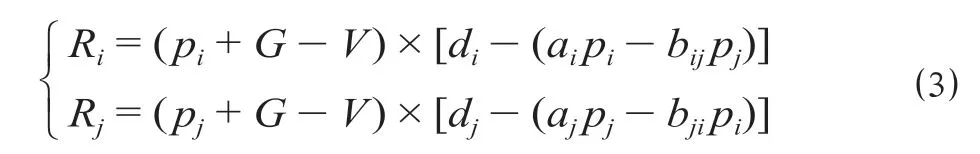
式中：Ri为重庆物流枢纽设施的运营收益，元；Rj为成都物流枢纽设施的运营收益，元；G为重庆与成都地方政府对单个集装箱运输的补贴力度，元/TEU。

假设成渝不存在主从关系，在完全理性的前提下同时在竞合策略中选择自身的最优策略[4]，从而可形成(竞争，竞争)，(竞争，合作)，(合作，竞争)，以及(合作，合作) 4 个策略组。

（1）当成渝为追求自身利益最大化而选择(竞争，竞争)策略时，对公式 ⑶ 分别求解一阶导，可得出

（2）当成渝选择(竞争，合作)策略时，表示重庆以自身利益最大化为目标采取竞争策略，而成都以整体收益最大化为目标采取合作策略。此时均衡条件为

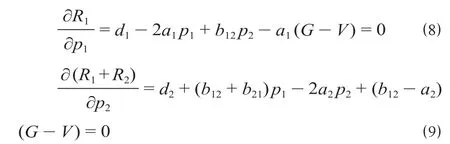
则求解出在(竞争，合作)策略组下重庆物流枢纽的收益函数和成都物流枢纽的收益函数分别为

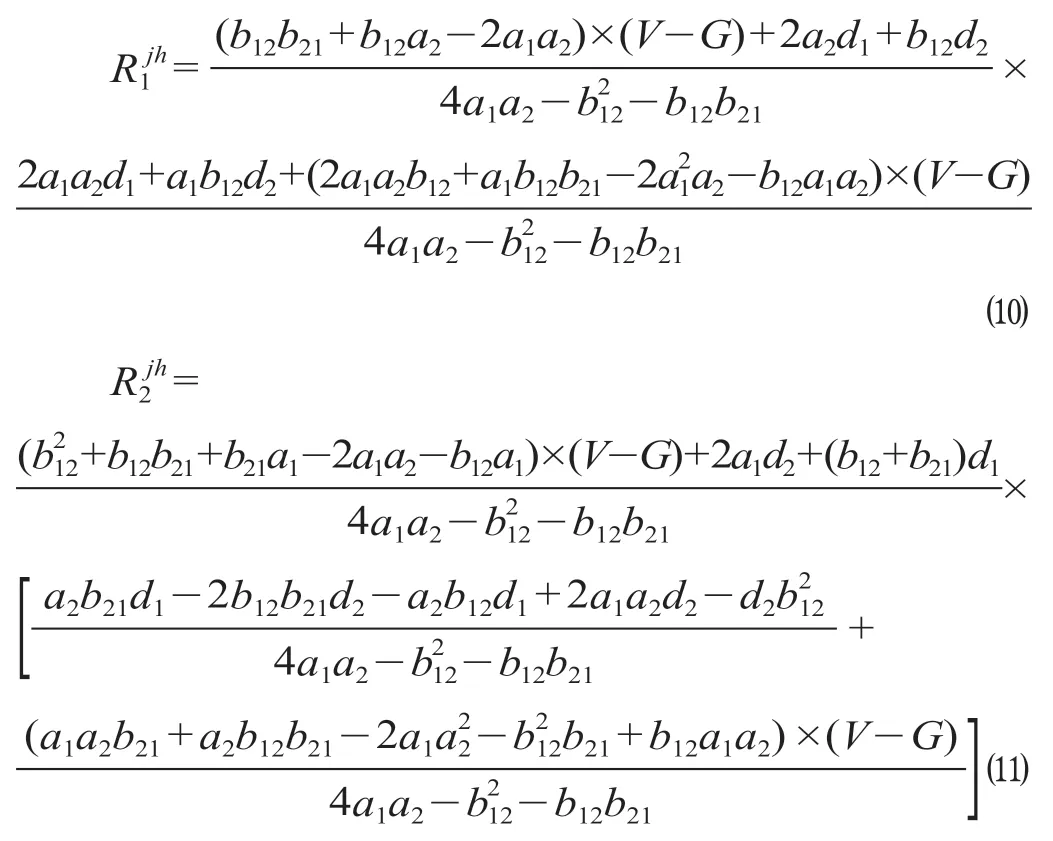
（3）当成渝选择(合作，竞争)策略时，表示重庆以整体收益最大化为目标采取合作策略，而成都追求自身利益最大化而采取竞争策略，此时在满足均衡条件下可以求解出在(合作，竞争)策略组下重庆物流枢纽的收益函数和成都物流枢纽的收益函数分别为

（4）当成渝选择(合作，合作)策略时，即双方为追求整体利益最大化都采取合作策略，此时在满足均衡条件下可以求解出在(合作，合作)策略组下重庆物流枢纽的收益函数和成都物流枢纽的收益函数分别为

1.2 成渝物流枢纽动态竞合博弈模型构建

由于重庆与成都竞合策略博弈是一个长期的、动态的过程，使用静态博弈模型很难一次性找到最优的稳定策略，因此运用演化博弈在静态竞合博弈基础上继续分析。假设成渝均为有限理性者，并在演化博弈过程中会根据自身利益不断模仿和调整策略。相比于纳什均衡，演化博弈的稳定均衡解更具说服力[4]。因此，建立复制动态方程是成渝竞合演化博弈的核心。为了保持模型数据的连贯性，成渝演化博弈复制动态方程的构建是基于静态竞合博弈矩阵，可以推出重庆、成都的演化复制动态方程如下。

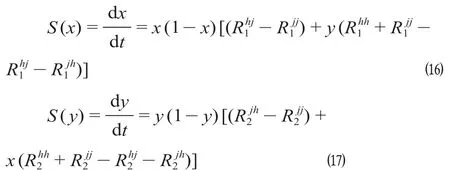
式中：S(x)为重庆选择竞合策略的复制动态方程；S(y)为成都选择竞合策略的复制动态方程；和为重庆和成都均选择竞争策略时的各自运营收益，万元；和为重庆选择合作、成都选择竞争策略时的各自运营收益，万元；和为重庆选择竞争、成都选择合作策略时的各自运营收益，万元；和为重庆和成都均选择合作策略时的各自运营收益，万元；x为重庆采取合作策略的概率，1 -x为竞争概率；y为成都选择合作策略的概率，1 -y为竞争概率。

1.2.1 稳定策略分析

假设在竞合演化博弈中，成渝的竞合策略选择比例趋于稳定，双方的复制行为处于均衡状态。通过利用雅克比矩阵J的行列式De(J)和其迹Tr(J)求解出成渝动态复制方程存在O(0，0)，A(0，1)，B(1，0)，C(1，1) 和D(x1，y1)5 个局部均衡点。均衡点局部稳定性情形如表1 所示。

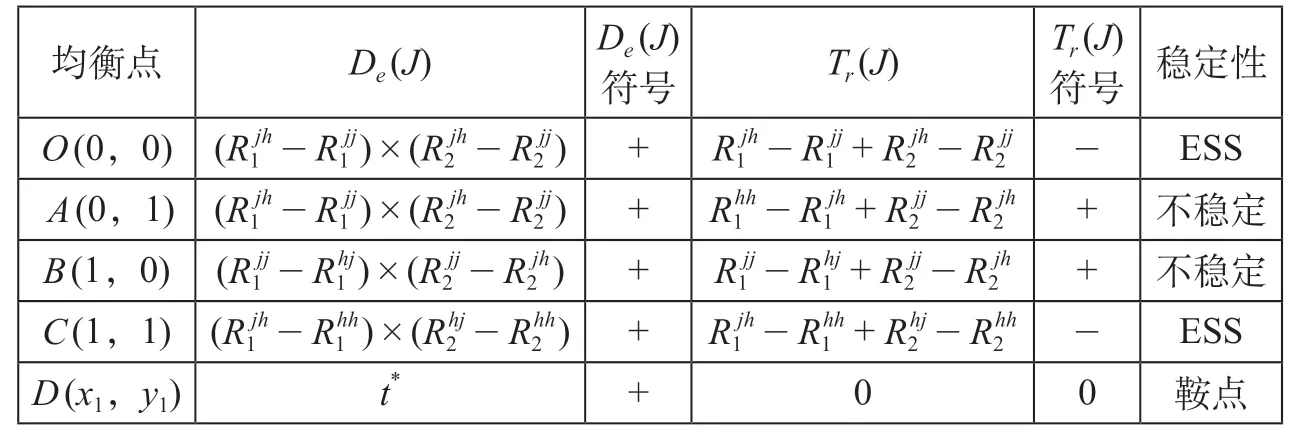
表1 均衡点局部稳定性情形Tab.1 Local stability situation at the equilibrium point

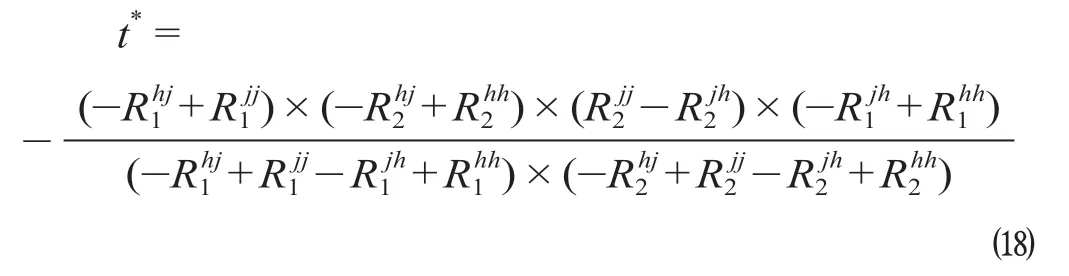
从行列式De(J)和迹Tr(J)的求解可知，A(0，1)和B(1，0)为双方竞合演化系统的2 个不稳定点，O(0，0)和C(1，1)为演化均衡点以及D(x1，y1)为鞍点。且成渝演化路径和结果取决于双方策略选择的初始状态以及鞍点位置。

2 算例分析

2.1 问题描述及参数假设

作为西部陆海新通道物流枢纽建设的核心城市，重庆与成都均开行了中国至东盟国家的铁海联运运输班列，承担着连接西部地区对东盟等国家经济贸易往来的作用。其中，以重庆为核心的东、中通道的运输效率高于以成都为核心的西通道。目前，西部陆海新通道铁海联运货物运输需求量呈现持续大规模增长，区域货物集聚效应日益凸显。然而现阶段成渝在物流枢纽班列运输上并未达成合作，双方的同质化服务增加了其竞争态势，不利于区域资源的合理流动，并带来了成渝物流运输成本的增加和集装箱浪费的问题。因此，以成渝物流枢纽设施的南向运输班列为例对模型的有效性进行分析具有一定的参考性和代表性。通过调研得到2020 年重庆和成都铁海联运班列的集装箱运输量数据，并分别代入竞合博弈收益模型。设重庆运输需求量d1=6.5 万TEU，成都运输需求量d2=4 万TEU；设单位边际成本V为0.5 万元/TEU，政府补贴G为0.15 万元/TEU。并假设a1和a2满足1.1 :1[5]，则a1=0.3，a2=0.27；b12与b21分别为a1和a2的75%，则b12=0.2，b21=0.23。

2.2 模型分析

2.2.1 静态模型分析

运用软件对成渝在不同策略组合下的物流枢纽设施的运营收益进行求解，得出成渝竞合博弈收益矩阵如表2 所示。

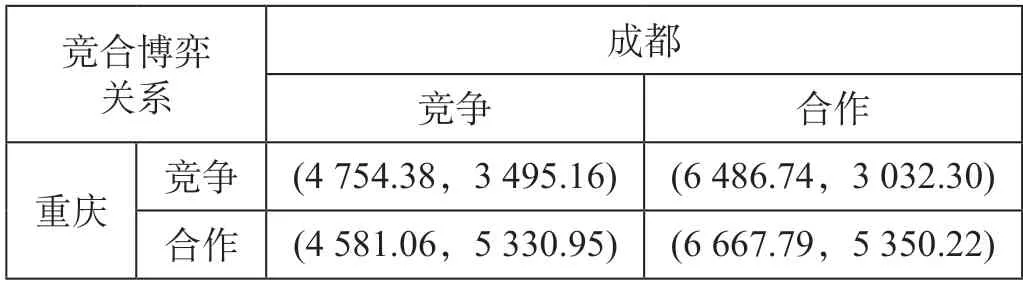
表2 成渝竞合博弈收益矩阵 万元Tab.2 Coopetition game income matrix of Chengdu and Chongqing

从表2 可知，若重庆和成都选择合作策略均能获得最优收益，基于团体最优的目标下双方的最优策略为(合作，合作)。而当重庆选择合作策略时，若成都从采取合作策略转变为竞争策略，此时成都的收益将会从5 350.22 万元下降至5 330.95万元，而重庆的运营收益将从6 667.79 万元下降至4 5810.6 万元，且小于双方都选择竞争策略时获得4 754.38 万元的收益。若成都选择合作策略时，重庆从采取合作策略转变为竞争策略，此时重庆的收益将由6 667.79 万元减少至6 486.74 万元，而成都的收益将由5 350.22 万元减少至3 032.30 万元，且小于双方都选择竞争策略时获得3 495.16 万元的收益。因此，促进成渝在物流枢纽运营上的合作并确保双方合作的长期稳定性十分必要[6]。

2.2.2 演化模型分析

由于演化博弈模型的参数与静态博弈模型保持一致，根据表2 及公式 ⒃、公式 ⒄ 计算出重庆与成都的复制动态方程如下。

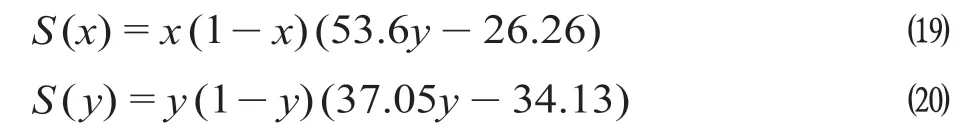
此时，求解出演化鞍点为D(0.921 2，0.489 9)。

运用软件对假设数据进行仿真得到成渝竞合博弈策略演化收敛图，重庆与成都竞合策略演化收敛图如图1 所示。A(0，1)和B(1，0)为成渝竞合博弈演化系统的2 个不稳定均衡点，O(0，0)和C(1，1)为该组合策略的演化均衡点，以及D(x1，y1)为竞合策略选择的临界点，亦为鞍点。由于x1，y1∈ [0，1]区间，当成渝的初始策略落在区域OADB内时，双方选择竞争策略的概率逐渐增加，最终竞合演化博弈的均衡点将收敛于点O(0，0)，即博弈稳定策略为（竞争，竞争）。同理，当其落在区域CADB内时，表明双方选择合作策略的概率不断加大，最终博弈策略收敛于点C(1，1)，即（合作，合作）为最终稳定策略。鞍点是影响成渝竞合博弈演化结果的关键因素，当鞍点越接近C点，区域OADB的面积越大，演化稳定策略收敛于O点的概率越大。鞍点越接近O点，区域CADB的面积越大，演化稳定策略收敛于C点的概率越大。因此，(竞争，竞争)和(合作，合作) 2 个策略组均为博弈模型的演化稳定解，且策略选择的区域面积为演化均衡解的概率[7]。因此，设区域面积OADB为S1，区域CADB面积为S2，可得出

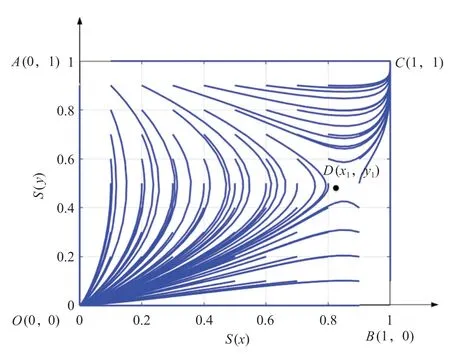
图1 重庆与成都竞合策略演化收敛图Fig.1 Evolution and convergence of coopetition strategy in Chongqing and Chengdu

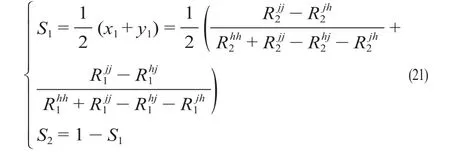
由上述公式计算可知：S1=0.705 6，表明成渝向(竞争，竞争)策略组演化的概率为70.56%；S2=0.294 4，表明双方向(合作，合作)策略组演化的概率为29.44%。

演化策略的方向取决于成渝策略选择的初始状态，为了更直观地研究初始状态对演化策略的影响程度，对S(x)和S(y)在[0，1]概率区间内进行定点分析，其中，0 表示成渝趋向于选择竞争策略，1 表示双方趋向于选择合作策略。以每隔0.2的步长来研究成渝竞合关系在不同概率区间内的走向[6]。利用软件进行模拟演化，得到成渝竞合策略演化路径仿真图如图2 所示。

从图2 可以看出，成渝选择竞争合作策略的概率是由双方策略选择的初始状态决定的。当重庆或者成都倾向于选择竞争策略时，此时对方必然只会选择竞争策略。此外，成渝在长期竞合策略演化过程中发现选择合作会获得较高的额外收益，由此便不断增加了双方选择合作策略的概率。然而通过分析图2 可知，只有成都选择合作的概率高于80%时，重庆才会最终趋向于选择合作策略。反之亦然。这是因为只有成渝选择合作策略意愿十分强烈时，才可以避免当其中一方改变为选择竞争策略，另一方会出现巨额经济损失的情况，从而实现双方达成最终的合作；如果成渝任何一方采取竞争策略，则在后续的策略选择中双方均不会选择合作策略。所以图2 不仅可以表示出成渝在不同概率区间内的竞合博弈走向，还可以表示成渝在不同概率区间内对合作和竞争策略的取舍情况。该趋势反映了成渝双方为了获得稳定的最优收益，不会轻易选择合作策略，而是会倾向于选择竞争策略，这就导致成渝在长期竞合演化过程中呈现选择竞争策略的概率远远大于合作策略的局面[8]。

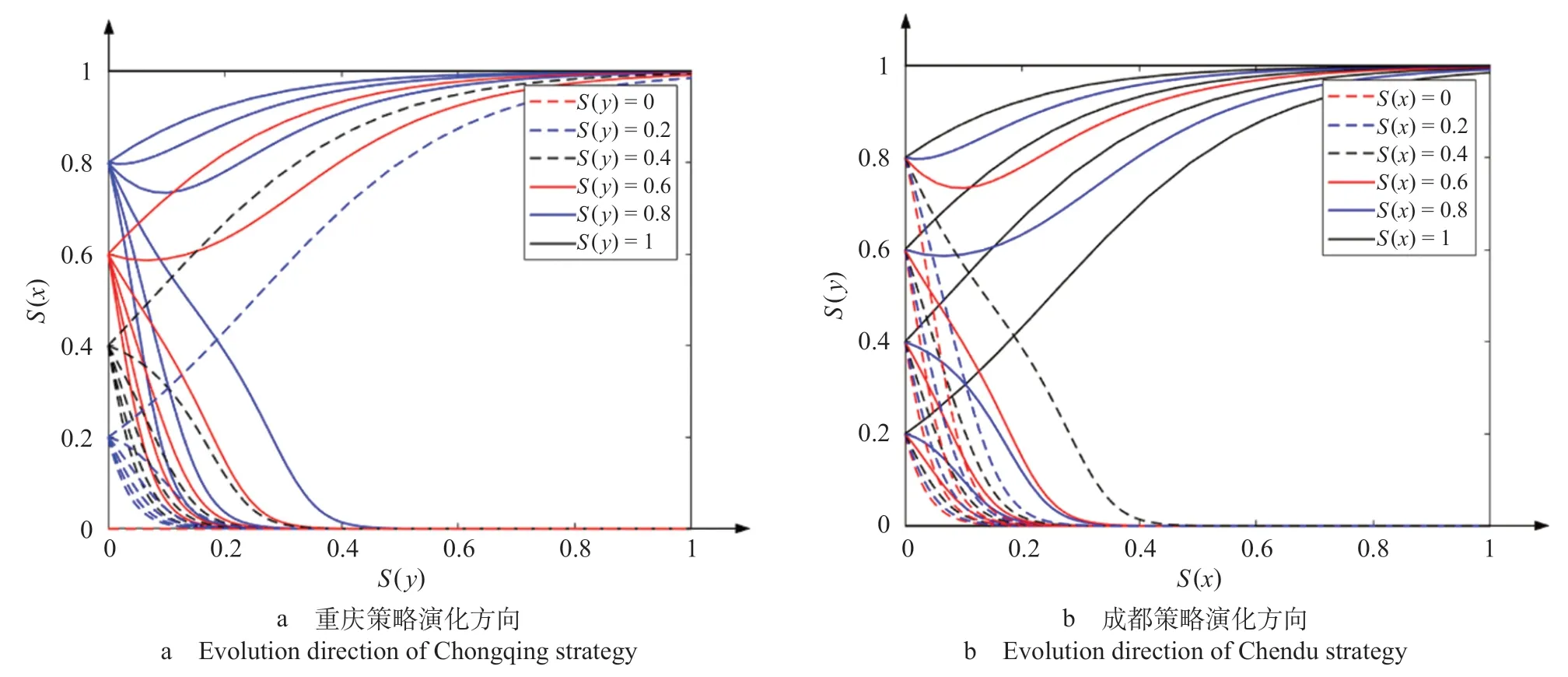
图2 成渝竞合策略演化路径仿真图Fig.2 Simulated evolution path for the coopetition strategy in Chongqing and Chengdu

2.3 结果分析

从成渝在物流枢纽运营上的竞合博弈收益变化和长期演化趋势的角度来分析重庆与成都的竞合关系，可得出以下结论。

（1）成渝物流枢纽竞合演化博弈存在2 个均衡解。一是双方选择(竞争，竞争)策略组进行分散决策，另一个是双方选择(合作，合作)策略组进行集中决策。(竞争，竞争)策略组是成渝双方在信息不对称情况下形成的劣势均衡解，此时成渝通过博弈获得的收益处于最小化。而(合作，合作)策略组是成渝货物资源合理配置的团体最优状态。通过分析成渝竞合收益矩阵可知，成渝收益最优的博弈策略是(合作，合作)，带来的最终收益为(6 667.79，5 350.22)。如果成渝在竞合博弈中不以合作为出发和归属点，而是以自身利益最大化为最终目的均选择竞争策略，势必导致其收益下降至(4 754.38，3 495.16)。从收益风险视角来看，成渝选择合作集中决策是成渝收益最优的均衡策略。因此，成渝地方政府应该采取适当的措施，避免双方在物流枢纽运营上的竞合博弈趋于劣势均衡，应引导双方向最优均衡策略(合作，合作)无限靠近。

（2）博弈一方的策略选择将影响另一方的策略选择，最终影响成渝竞合博弈演化走向。①当重庆追求自身利益最优时选择竞争策略，此时成都若选择合作策略将会造成自身收益损失，则只能选择竞争才能获得稳定的最优收益。同理重庆也将面临相同的情况。②当重庆以团体利益最优为目标时选择合作策略，会将自身在物流枢纽班列运输的收益让渡一部分给予成都，主动分享相关信息，这在一定程度上将市场的货源分流到成都内部；此时成都若为了获得额外的风险收益而选择竞争策略时，将会让重庆由于选择合作策略面临严重的利益损失，并造成双方在后续的时期内不会再选择合作策略。反之亦然。③当重庆或者成都选择合作的意愿十分强烈时，将会增加对方最终选择合作策略的概率，这有利于促进双方向最优策略(合作，合作)靠近，但成渝的合作关系不能维持稳定时，将会影响成渝放弃合作而转向选择竞争策略。

（3）促进成渝由非合作策略转变为合作策略，避免双方在物流枢纽运营上出现“囚徒困境”问题，从而实现成渝团体收益的长期最优化。若成渝选择(合作，合作)最优均衡策略时，表明双方会以长期整体收益最优为目标集中决策，此时双方运营收益均为最高。但从长期演化趋势来看，在不被外部环境干预的情况下，成渝向(竞争，竞争)策略组演化的概率明显高于向(合作，合作)策略组收敛的概率。这是由于政府的补贴政策会在一定程度上降低成渝物流枢纽的运输成本以及增加双方采取竞争策略的风险收益。成渝若已知对方会采取合作策略时，会将自身策略从合作转变为竞争来作为占优策略并重新定价，直至自身定价低于对方的服务价格从而达到抢占市场需求量的目的来获取风险收益，最终导致成渝竞合博弈达至(竞争，竞争)的劣势均衡策略。从整体效益来看，由于成渝合作往往不是一次性的，若成渝在长期发展过程中仍选择竞争策略，一定程度上不利于营造良好的市场秩序，并导致成渝双方物流运输成本的增加以及集装箱的大量浪费。而成渝都选择合作策略时，双方不仅能够获得长期稳定的额外收益，还可以通过合作来整合提速成渝班列运输线路，进一步突显西部陆海新通道物流枢纽的运输优势，实现成渝经济竞争力的提升和区域资源的协调分布。因此，在长期发展过程中促进成渝由非合作策略转向选择合作策略无疑是更明智的选择，维护良好稳定的合作关系更能够实现成渝经济上的“双赢”[9]。

为了避免成渝在物流枢纽运营上出现“个人理性”与“团体理性”的“囚徒困境”问题，需要促进成渝建立共商共建共享的合作关系，从而提高西部陆海新通道物流枢纽的经济效益。首先，成渝地方政府应出台相应政策，适时调整对双方物流枢纽运营的补贴力度，避免出现不公平的竞争优势来干扰市场正常运行的现象，同时，成渝地方政府的补贴行为应更具针对性，且补贴的资金去向应更清晰透明，最大化发挥补贴政策效应，从而促进成渝建立合作关系，有利于提高双方物流枢纽的运行效率。其次，地方政府通过营造良好的内外部环境发挥引领作用，以西部陆海新通道物流枢纽联盟为依托构建完善的协同发展机制，推动成渝更深层次的交流合作，更好地促进成渝在物流枢纽运营上发挥各自优势，凝聚双方发展合力，从而降低双方的运输成本和减少集装箱的浪费。最后，成渝地方政府依托物流枢纽联盟平台，加强双方物流枢纽运营之间的交流和经验分享，建立和完善多层次的合作机制，共同构建双方物流枢纽运输产业协同[10]。此外，在实现资源和信息共享的前提下，地方政府通过出台各种优惠政策有利于降低成渝合作的收益风险，实现双方长期合作的稳定性。

3 结束语

针对成渝在物流枢纽运营中的竞合问题，构建了成渝静动态竞合博弈收益模型，随后以双方运输班列为例分析了其竞合策略选择及演化趋势，有助于为促进成渝在物流枢纽运营上的合作提供理论依据和研究思路。研究表明：成渝竞合博弈模型存在(竞争，竞争)策略组的劣势均衡解和(合作，合作)策略组的最优均衡解。但从收益效果来看，成渝合作集中决策是双方运营的最优解。因此，成渝在西部陆海新通道建设运营发展过程中，为了避免竞合关系出现“囚徒困境”问题，促进成渝在自身发展与社会资源优化配置的双重目标下，实现双方向最优策略(合作，合作)无限靠近的局面，才能更好地促进成渝建立有序竞争、共商共建共享的合作关系，有助于促进区域资源的整合和优化，推动西部陆海新通道高质量发展。