基于预测模糊PID 控制算法的高速列车优化控制研究

杨宏阔，侯 涛，陈 昱

（兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

0 引言

高速列车作为一种重要交通方式，具有快捷舒适、平稳安全、节能环保等特点，深受旅客的欢迎，世界各国都大力发展高速列车来满足日益增长的出行需求。高速列车速度控制的效果直接影响其安全、舒适、高效和准点运行等性能指标。

国内学者最早对高速列车建模的研究一般都是对列车运行时的受力情况进行详细分析，主要是单质点模型。于振宇等[1]提出面向控制的列车制动模型，仿真表明该模型能够很好地描述列车的运动特性。石卫师[2]以此单质点模型为基础进行了基于无模型自适应控制的城轨列车自动驾驶研究，但未考虑参数优化，只是以该模型为基础，结合真实的列车参数进行了模型参数寻优设计。在设计控制器方面，Aradi 等[3]将预测控制应用到列车自动驾驶系统中，在模型失配的情况下，也能实现无静差控制，但动态矩阵控制DMC 算法存在动态时间较长的问题。史来诚[4]提出基于黏着与滑模控制的列车速度控制方法，有较好的鲁棒性，但存在抖振现象。连文博等[5]针对高速列车传统PID控制器在强干扰作用下稳定性不高、鲁棒性差的缺点，提出一种基于自抗扰控制ADRC 的高速列车速度控制算法。张驰等[6]将分数阶PID 控制算法应用到地铁列车中，使列车实现更优的速度控制，但列车的档位控制存在一定的缺陷。

因此，基于优化后的列车模型，研究采用预测模糊PID 控制算法实现对列车目标速度曲线的在线快速精确追踪。该方法改善了高速列车速度控制系统的性能，进一步提高高速列车的速度控制效果，确保高速列车在运行中的快速性、平稳性与准时性。

1 高速列车运动模型

将列车整体看作一个高速列车的单质点模型时，通过忽略各车厢间的耦合力和速度偏差，来建立高速列车运行过程的单质点机理模型。高速列车运动模型如图1 所示。高速列车运动模型反映的是控制器输出控制量、加速度与速度三者之间的动态关系。

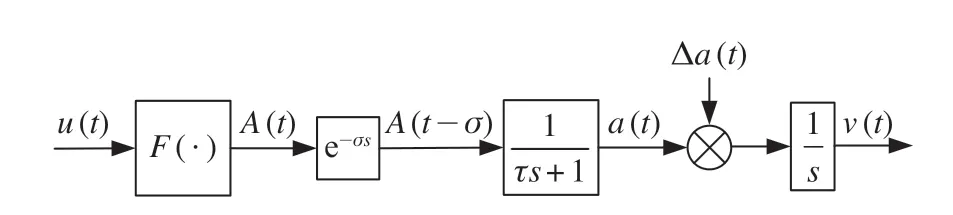
图1 高速列车运动模型Fig.1 Motion model of high-speed trains

图1 中，u(t)为控制指令；F(·)为静态函数；A(t)为期望加速度，m/s2；σ为传输延时；τ为系统时间常数；s为复变量；a(t)为控制加速度，m/s2；Δa(t)为干扰加速度，m/s2；v(t)为输出速度，m/s。静态关系函数[1]计算公式为

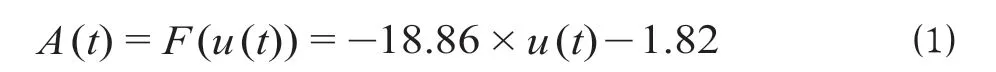
1.1 模型参数寻优

动态响应参数包括系统时间常数τ和传输延时σ。参数寻优过程如图2 所示。

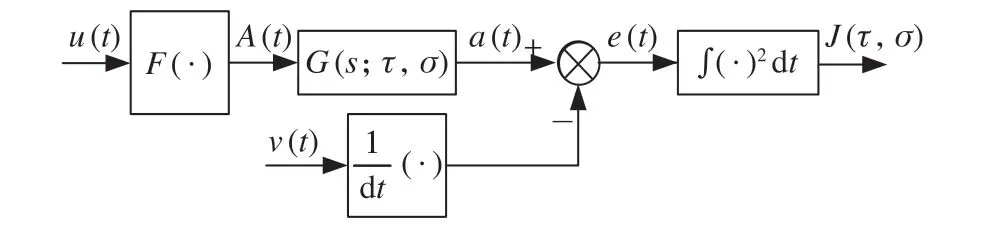
图2 参数寻优过程Fig.2 Parameter optimization process

期望加速度到控制加速度的传递函数可表示为G(s；τ，σ)。相同的输入下，最佳的参数使系统G的响应误差e(t)最小，e(t)的计算公式为

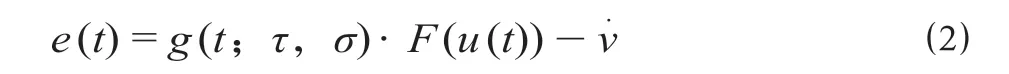
式中：g(t；τ，σ)=L-1[G(s；τ，σ)]。

误差的大小用公式 ⑶ 进行评价。

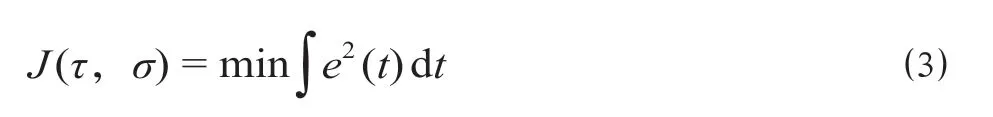
1.2 列车牵引力计算

CRH3 型动车组的牵引特性用公式 ⑷ 计算，牵引特性图如图3 所示。

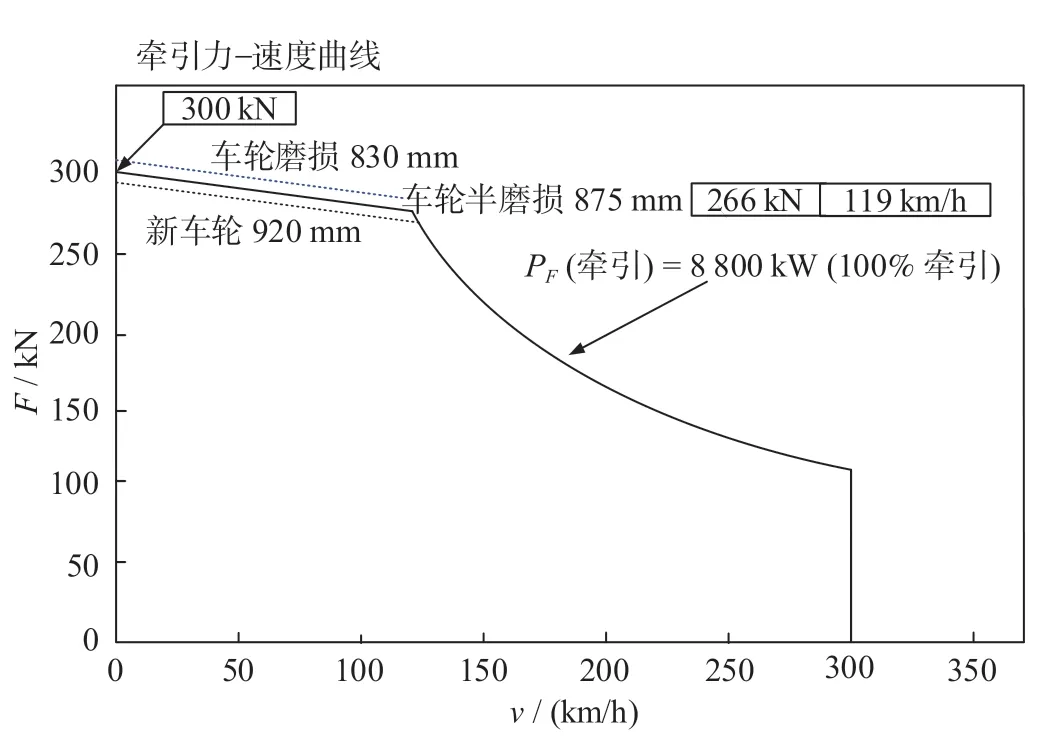
图3 牵引特性图Fig.3 Traction characteristic diagram

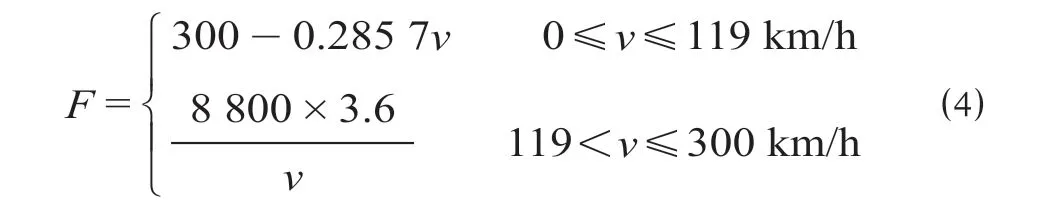
1.3 列车制动力计算

CRH3 型动车组的制动特性计算如公式⑸所示，制动特性图如图4 所示。

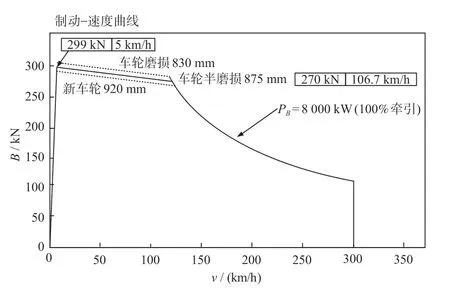
图4 制动特性图Fig.4 Braking characteristic diagram

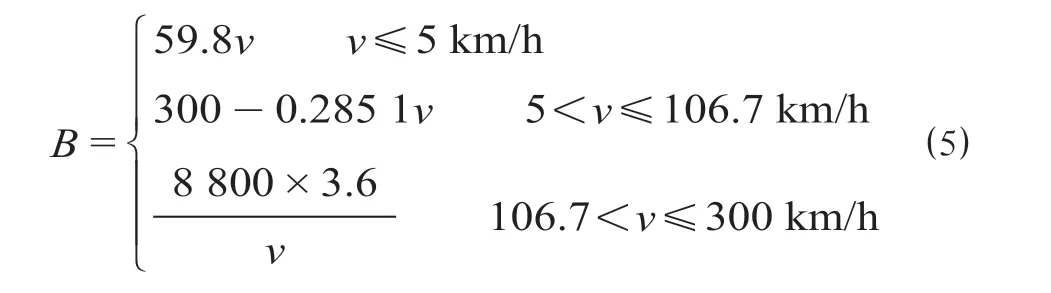
1.4 参数辨识

1.4.1 基本阻力

CRH3 动车组单位基本阻力公式为

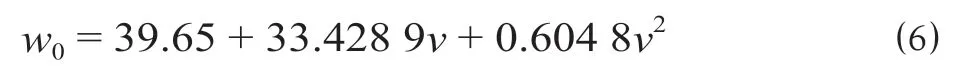
式中：w0为基本阻力，N；v为动车组速度，m/s。

1.4.2 附加阻力

附加阻力主要包括坡道附加阻力、曲线附加阻力、隧道附加空气阻力3 部分。其中，坡道附加阻力对列车运行的影响最显著。目前只对坡道附加阻力进行优化计算。

（1）坡道附加阻力。

①第1 种情况。整个列车的长度位于同一段坡道上，则列车的单位坡道阻力wp计算公式为

式中：i为坡度值。

②第2 种情况。列车整个长度同时位于几个坡段，坡道阻力的计算按照列车在每段坡道上的长度所占列车总长的比例累加计算。l为列车长度，l1，l2，…，ln为列车在不同坡度上的长度，则列车的单位坡道阻力计算公式为

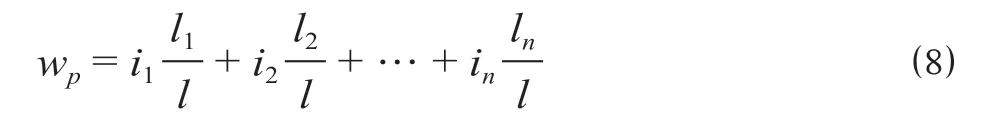
通过对线路数据的处理提高变坡点附近受力计算的精度。坡道计算流程如图5 所示。

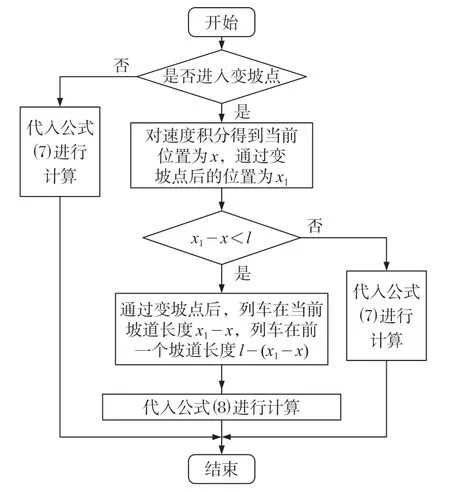
图5 坡道计算流程Fig.5 Ramp calculation flow

图5 中动车组总长l=200 m，取郑西高速铁路(郑州东—西安北)华山北—西安北坡道数据进行如图5 所示的坡道计算，起点里程950.62 km 至终点里程1 003.519 62 km，共计52.899 62 km，22组数据[7]。列车位置每变化10 m，取一组数据进行计算。即在列车跨越变坡点时，坡道阻力也是渐变的，因而速度曲线是光滑过渡的，更接近实际。例如，第2 个变坡点线性关系为

（2）曲线附加阻力。在弯道上运行时所受的单位曲线附加阻力计算公式为

式中：wq为曲线附加阻力，N/kN；R为曲线半径，m。

（3）隧道附加空气阻力。单位隧道附加空气阻力计算公式为

式中：wr为隧道附加空气阻力，N/kN ；Ls为隧道长度，m。

2 预测模糊PID 控制算法设计

预测模糊PID 控制原理图如图6 所示。图6 中，yr为目标速度，m/s；yp为反馈校正后的速度，m/s；ym为预测速度，m/s；y为输出速度，m/s；U为控制器输出的控制量。

图6 预测模糊PID 控制原理图Fig.6 Principle of predictive fuzzy PID control

2.1 预测控制算法的设计

动态矩阵控制是增量式预测控制算法，能有效克服过程的不确定性、大滞后性和关联性。设a=[a1，a2，…，an]为被控对象的预测模型向量，未来时刻的P个预测向量[8]计算公式为

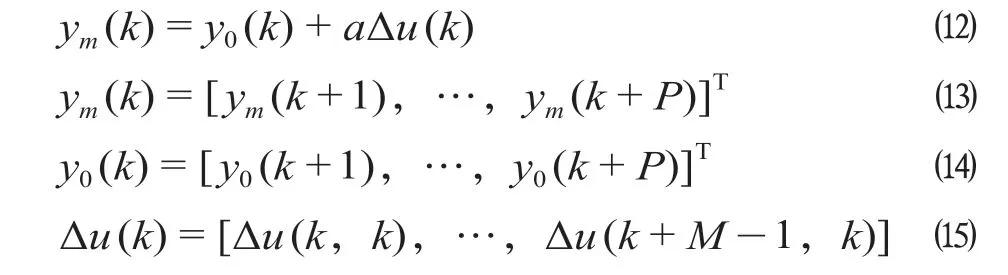
式中：y0(k)为初始值；ym(k)为m时刻的输出值；P为预测时域长度；m为控制时域长度；(k+1，k)表示在k时刻对k+1 时刻的预测[9]。

预测的误差计算公式为

式中：y(k+1)为k+1 时刻的实际输出值。

采用滚动优化的方式对输出预测值进行校正，计算公式为

式中：h为校正向量；yp(k+1)为校正完成后的值。

2.2 模糊PID 控制算法的设计

选取列车速度跟踪偏差e的模糊子集为{NB，NM，NS，NO，PS，PM，PB}，列车速度跟踪偏差变化率ec的模糊子集为{NB，NM，NS，NO，PS，PM，PB}，输入速度偏差与偏差变化率，利用模糊控制规则对PID 参数进行修整[10-11]。以ΔKP为例，ΔKP模糊控制规则如表1 所示。

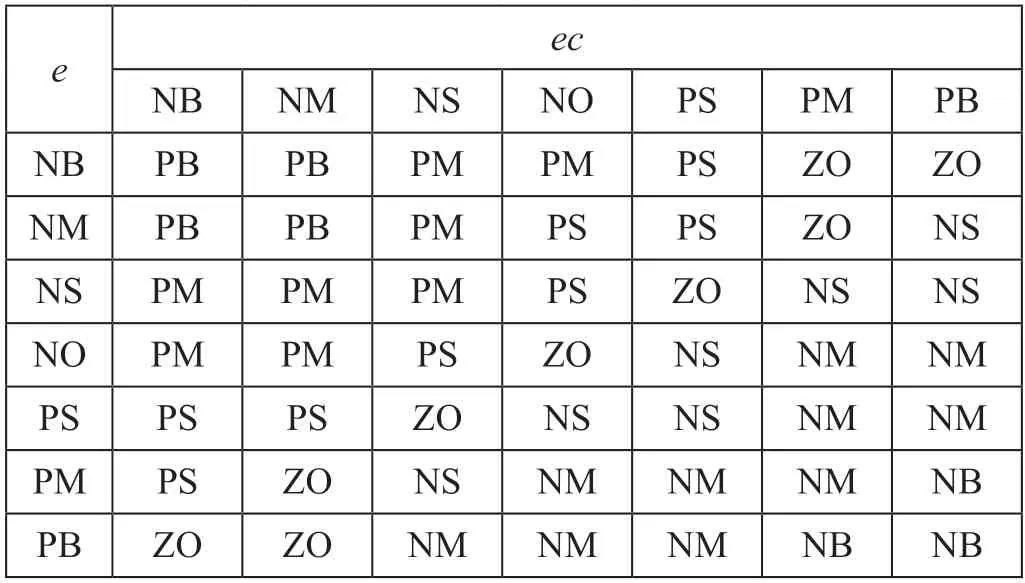
表1 ΔKP 模糊控制规则Tab.1 Fuzzy control rules of ΔKP

3 系统仿真

3.1 仿真线路、仿真模型与控制算法参数设置

按照列车牵引制动曲线的计算公式，得到列车理想速度曲线如图7 所示。

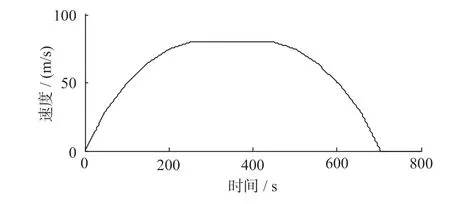
图7 列车理想速度曲线Fig.7 Ideal speed curve of trains

在预测模糊PID 控制中，速度偏差e的论域为[-1，1]，偏差变化率ec的论域为[-6，6]，控制量的论域为[-3，3]，量化因子Ke=3，Kec=0.5，Ku=1。初始参数Kp=1.2，Ki=0.5，Kd=1，二阶模糊控制器对Kp，Ki，Kd3 个系数进行在线校正，校正系数Δkp=2.5，Δki=3，Δkd=3。DMC 控制中阶跃响应在25 s 左右时基本达到稳定，模型向量应该包含被控对象的所有动态性能，因而选取采样周期TS=0.5，建模时域N=40，控制时域m=2，优化时域P=15[13]。

高速列车仿真模型如图8 所示。

图8 高速列车仿真模型Fig.8 Simulation model of high speed trains

3.2 仿真结果

通过公式⑶可估计出系统时间常数和传输延时的最优值：σ=0.8 s，τ=0.4 s。为评估模型参数的有效性，分别取不同参数进行仿真，不同参数下的速度跟踪误差如图9 所示，不同参数下的速度跟踪误差局部放大图如图10 所示。

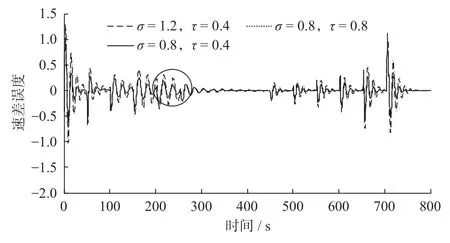
图9 不同参数下的速度跟踪误差Fig.9 Speed tracking error under different parameters

分析图10 的局部放大图可知σ=0.8 s，τ=0.4 s 时高速列车运动模型具有最优的性能。

图10 不同参数下的速度跟踪误差局部放大图Fig.10 Partial enlarged view of the speed tracking error under different parameters

郑西高速铁路华山北—西安北坡道线路数据(起点里程950.62 km 至终点里程1 003.519 62 km)如图11 所示，优化计算后的郑西高速铁路华山北—西安北坡道线路数据如图12 所示。

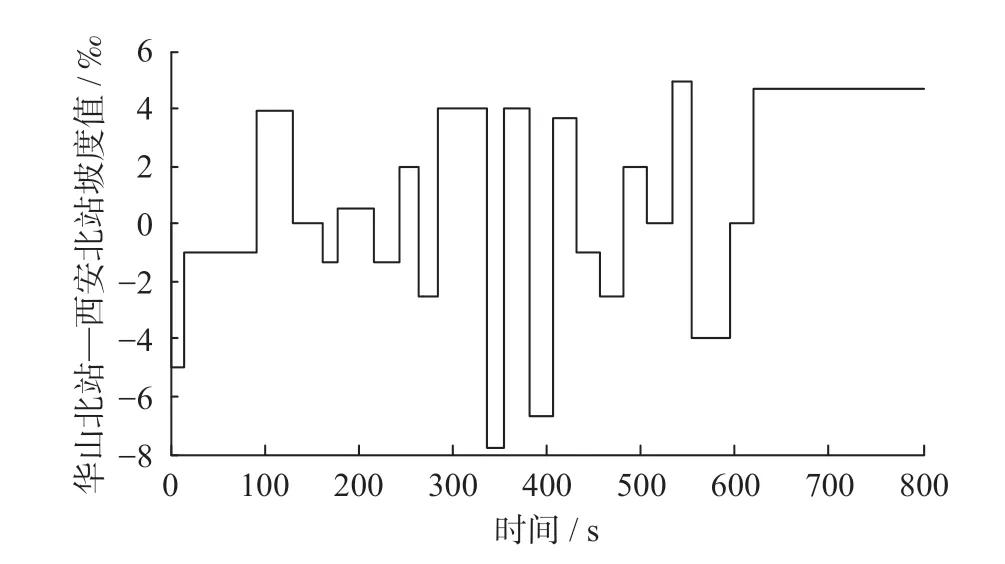
图11 郑西高速铁路华山北—西安北坡道线路数据Fig.11 Ramp data from Huashanbei Railway Station to Xi’anbei Railway Station on Zhengzhou-Xi’an High Speed Railway

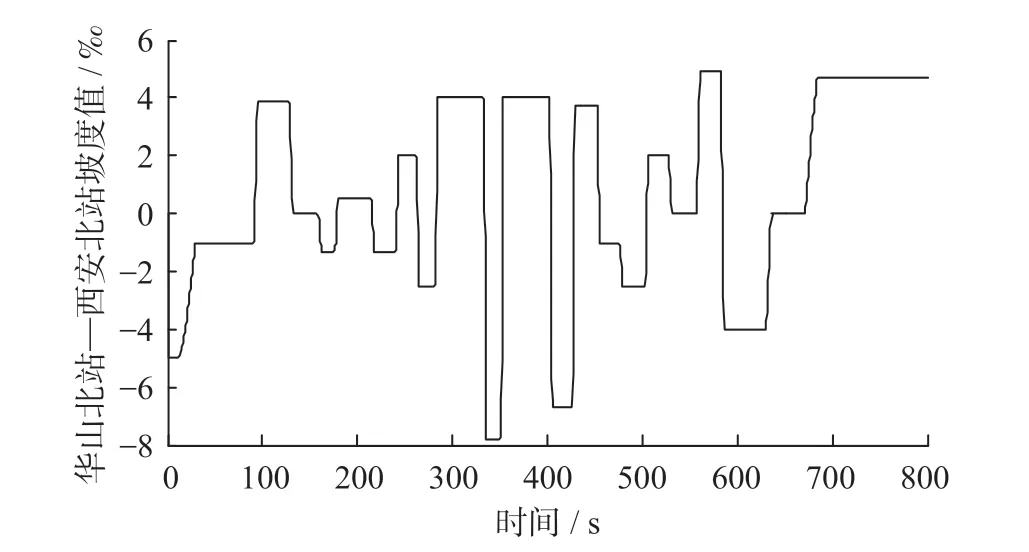
图12 优化计算后的郑西高速铁路华山北—西安北坡道线路数据Fig.12 Ramp data from Huashanbei Railway Station to Xi’anbei Railway Station on Zhengzhou-Xi’an High Speed Railway after optimal calculation

为体现坡道附加阻力优化计算方法的有效性，把原始坡道数据与优化后的坡道数据使用同一算法(预测模糊PID 算法)跟踪理想速度曲线进行对比，2 种坡道数据下的速度跟踪曲线图如图13 所示，速度跟踪曲线局部放大图如图14 所示。

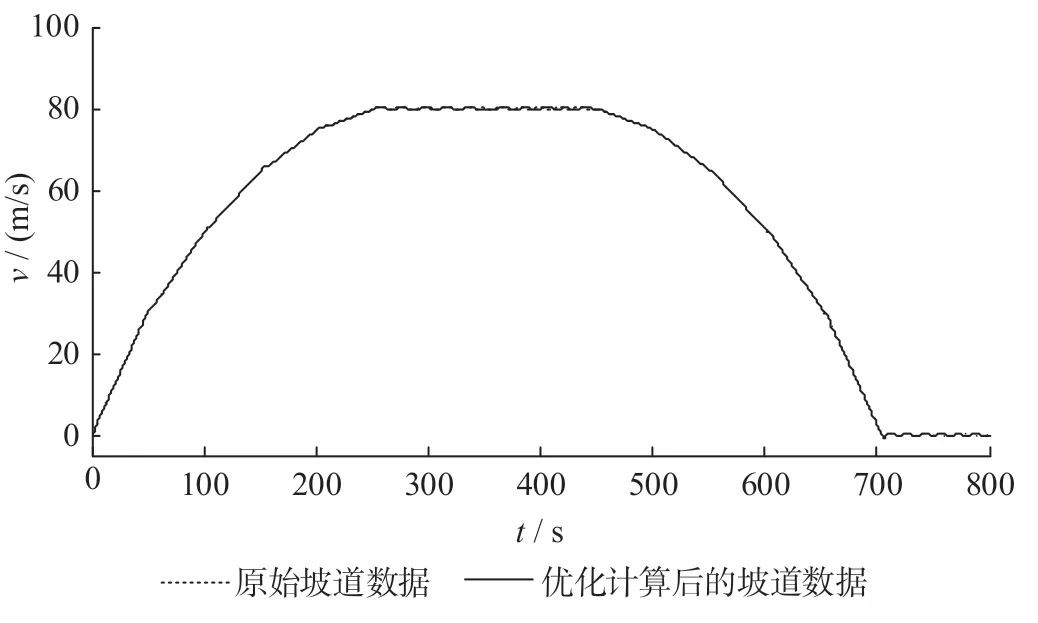
图13 2 种坡道数据下的速度跟踪曲线图Fig.13 Speed tracking curves under two sets of ramp data

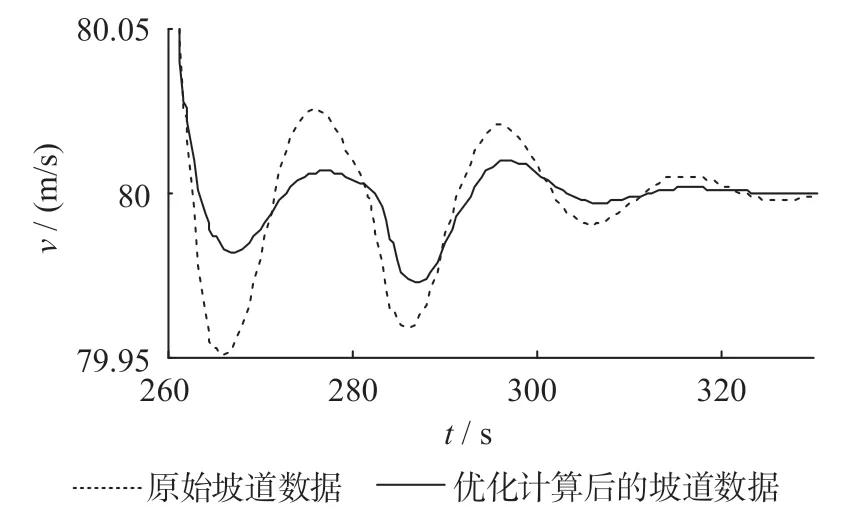
图14 速度跟踪曲线局部放大图Fig.14 Partial enlarged view of the speed tracking curves

由图13 可知附加阻力优化计算方法有效提高了变坡点附近受力计算的精度，减小了速度控制的误差。2 种控制算法下的速度跟踪曲线图如图15 所示。2 种控制算法下的速度跟踪曲线局部放大图如图16 所示。2 种算法的ITAE 指标如图17所示。

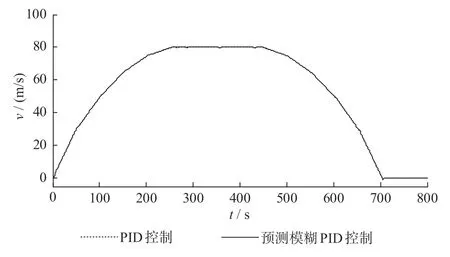
图15 2 种控制算法下的速度跟踪曲线图Fig.15 Speed tracking curves under two control algorithms

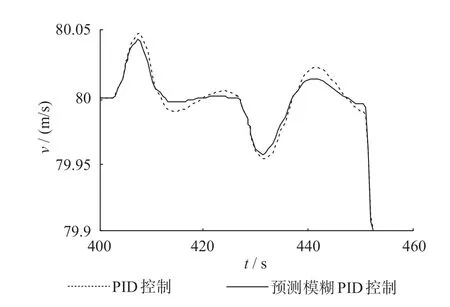
图16 2 种控制算法下的速度跟踪曲线局部放大图Fig.16 Partial enlarged view of the speed tracking curves under two control algorithms

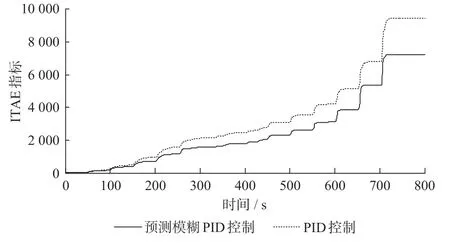
图17 2 种算法的ITAE 指标Fig.17 ITAE indicator of two algorithms

4 结论

通过对传统的列车运动模型进行改进，结合真实的列车参数进行模型参数寻优设计，得到以下结论。

（1）优化后的模型能以更小误差跟踪理想速度曲线，对高速列车运行中所受的阻力进行分析：由于传统单质点模型不考虑车长，列车在变坡点会造成较大的速度控制误差，因而结合真实线路数据提出了附加阻力优化计算方法，使得列车在变坡点受到的坡道附加阻力并非突变，转化为一个渐变的过程，更能真实地反映列车在线路上的实际运行情况。

（2）在优化后的列车运动模型基础上，针对高速列车速度控制的精度问题，将预测控制与模糊PID 控制相结合，基于高速列车模型设计了预测模糊PID 速度控制器，用于控制列车运行速度。由仿真可知，预测模糊PID 能有效降低高速列车速度控制误差。