多层软土地基中桩基水平承载计算研究

刘 越，黄 朝 煊

(浙江省水利水电勘测设计院，浙江 杭州 310002)

0 引 言

由于中国沿海滩涂区多为淤泥质软土地基，其工程建设开发中的桩基水平承载能力相对较差，对深厚淤泥质软土地基中桩基水平承载能力及桩基水平变位控制研究是十分重要的课题[1]。

软土地基中，桩基的水平承载课题是十分复杂的桩-土相互作用问题[2-4]。目前，国内桩基水平承载计算主要方法有：常数法、规范中经典m法[5](即忽略表层土水平反力系数)及吴恒立[6]中双参数法等。张磊等[7]参考Hsiung[8]等方法，进行了推广给出相应离散数值解。国外Matlock[9]等基于p-y曲线法对桩基水平变位计算进行了研究。黄朝煊等[10-12]基于经典m法对水平受荷桩进行深入总结性研究，黄朝煊等[13]还对软土地基预加固处理后桩基水平承载力提高影响进行了研究。

针对目前运用的JGJ94-2008《建筑桩基技术规范》中存在着桩基水平承载力计算水平抗力系数比例系数m取值模糊、未考虑黏性土黏聚力c引起的表层土水平抗力影响，而且不便于工程设计人员查算应用等问题。本文根据常微分方程的幂级数解法，在考虑黏性土黏聚力引起的表层土水平抗力影响下，对软土地基中桩基水平承载力及变位计算进行深入研究，以便于实际工程应用。

1 软土地基中桩基水平承载力及变位计算

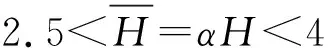
弹性理论下的桩身平衡微分方程[5]如下：

(1)

式中：p(x，y)为桩侧地基土水平抗力，对于线性反力则p(x，y)=ky，y为桩身水平变位，k为桩侧地基水平反力系数，对于考虑黏性土黏聚力引起的表层土水平抗力影响时取k=m(x+x0)(见图1)；x为桩深，m；x0为考虑黏性土黏聚力c引起的表层土水平抗力参数，m，当x0=0时，退化为文献[3]中m法；b为单桩计算宽，m，桩径D≤1.0 m时，b=0.9(1.5D+0.5)，桩径D>1.0 m时，b=0.9(D+1)。

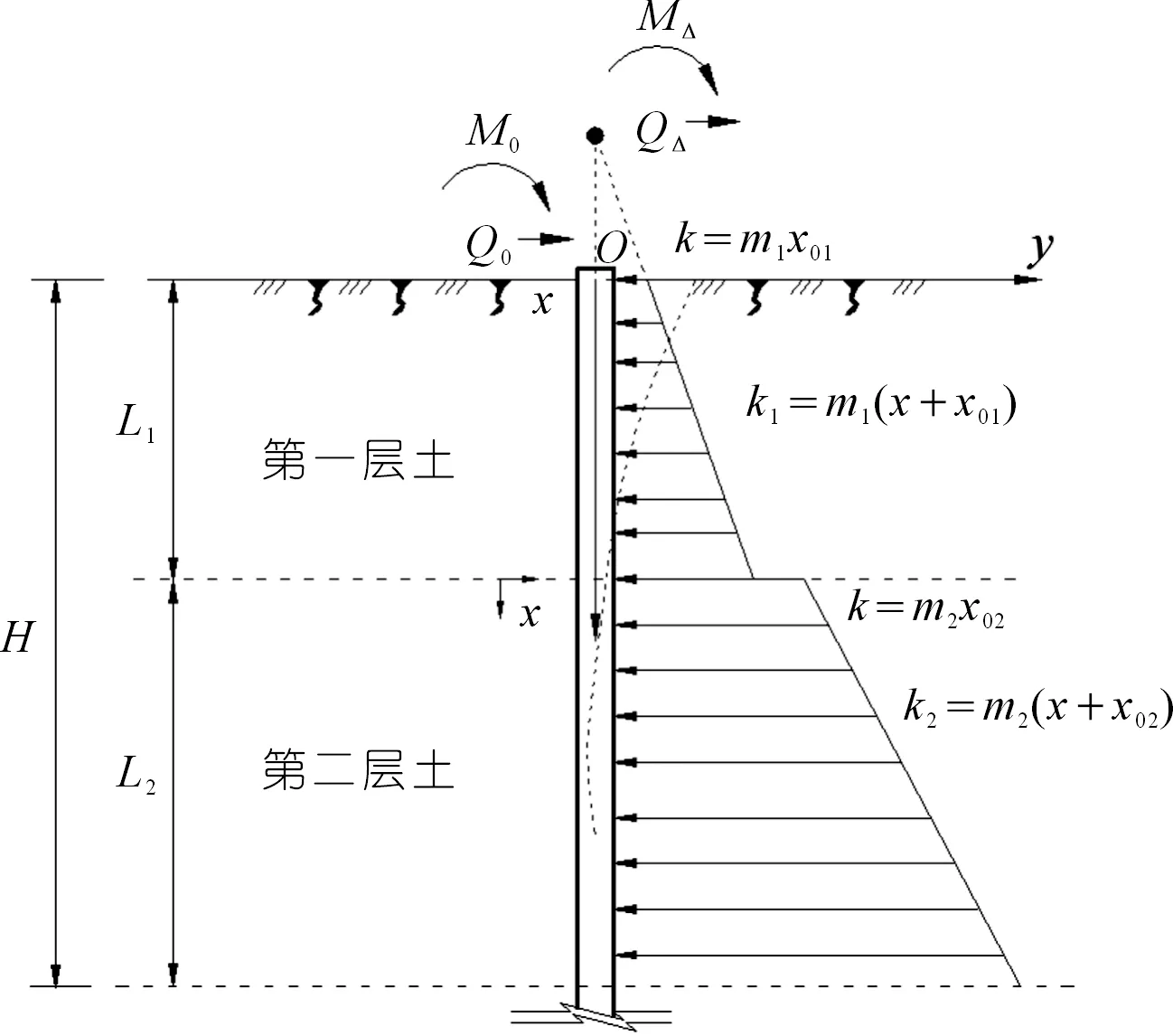
图1 单桩计算简图Fig.1 Diagram of single pile calculation

在图1中，参数Q0、M0分别为桩顶水平剪力和弯矩；参数Q△、M△分别为虚拟桩桩顶O处的水平剪力和弯矩。

1.1 多层地基土中单桩水平变位计算

第1层地基土中桩基的平衡方程如下[5]：

(2)

第2层地基土中桩基的平衡方程如下：

(3)

(4)

(5)

拟线性微分方程(4)、(5)满足边界条件：

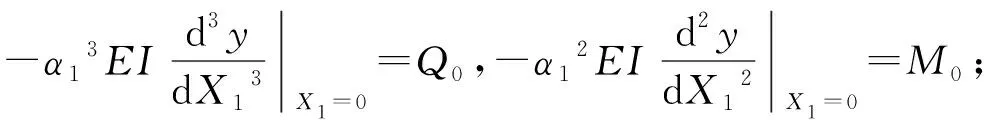
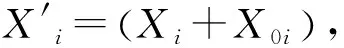
(6)

根据常微分方程的幂级数法，令：

(7)

根据式(6)和式(7)，得系数an的计算式：

(8)

其中，n!表示阶乘，利用文献[10]，可得桩身微分方程(2)、(3)的解析解：

(9)

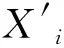
(10)

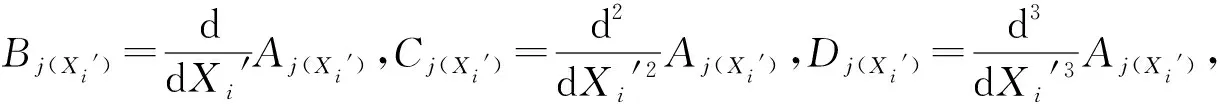
当桩顶自由时，利用边界条件得代数方程：

(11)

其中各矩阵为

(12)

(13)

(14)

(15)

待求系数列向量为

(16)

在桩顶嵌固情况下分块矩阵为

(17)

1.2 对于退化为单层土中的半刚性桩的设计计算(换算桩长αH>2.5)

半刚性桩满足桩底处弯矩、剪力均为0条件(见图2)。根据本文解析解(9)，利用Matab软件数值计算，得到半刚性桩桩顶水平位移及转角的解析解：

(18)

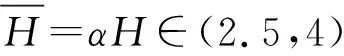
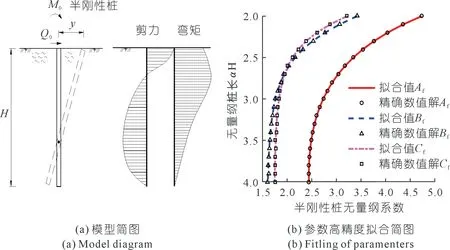
图2 半刚性桩计算图Fig.2 Calculation diagram of semi-rigid pile

(19)

由图2可知：无量纲参数Af、Bf、Cf是换算桩长的减函数，即半刚性桩桩长越长，则地基土对桩的侧向约束作用越大，桩身水平变位及转角则越小。对于柔性桩，即αH>4时，则参数Af、Bf、Cf取极限定值。

在实际工程中，为了节省工程投资，采用半刚性桩进行基坑支护时可采用本文解计算分析，这样方便快捷且精度可靠。

1.3 根据地基土抗剪强度指标计算柔性桩(αH>4)水平承载特性

对于地基水平抗力系数k，可参考文献[13]中的公式进行计算：

k=Ah+Bhxn

(20)

式中：Ah、Bh依据地基土的抗剪强度指标c、φ计算：

(21)

式中：γ为桩侧地基土容重，kN/m3；D为桩径，m。

根据参考文献[13]，可取C=40.0 kN/m3，n=0.40～1.0，Cm=1.0～2.0，参数Fw1=0.50～1.70，Fw2=2.00～4.40。

系数Nq、Nc和Nγ为

(22)

参考桩基规范[3]，取n=1.0。考虑到黏性土黏聚力c引起的表层土水平抗力作用下的地基土的线性反力系数计算公式为

(23)

对于黏性土，由于受到黏聚力c值的影响，当需要考虑表层土水平反力影响时，即地基土水平反力系数为k=m(x+x0)，根据虚拟桩法，令x′=(x+x0)，将其转换为虚拟桩。根据本文1.1节求解方法，给出受到黏聚力c值的影响时不同桩深处的位移、转角、弯矩以及剪力的计算式：

(24)

其中，系数Ay、By、Aθ、Bθ、AM、BM、AQ及BQ根据Matlab软件计算给出，如表1所列。待定参数MΔ、HΔ为虚拟法的桩顶弯矩、剪力(见图1)，结合实际桩顶边界条件联立方程给出，详见后文。

(1)对于桩顶自由情况下，根据实际桩顶边界条件M(X′)|X′=X0=M0，Q(X′)|X′=X0=Q0联立方程求解，得到待定参数MΔ、HΔ如下：

(25)

将式(25)代入虚拟桩法解析解(24)，便可给出桩顶自由情况下的解析解。取X=0(X′=(X+X0)=X0)，即可得对于考虑表层土水平反力影响时，桩顶自由情况下的桩顶水平位移为

(26)

依据桩顶水平位移允许值χ0a，推求得到桩顶自由时的水平承载力计算式如下：

(27)

(2) 对于桩顶嵌固情况下，根据实际桩顶边界条件φ(X′)|X′=X0=0、Q(X′)|X′=X0=Q0联立方程求解，得到待定参数MΔ、HΔ如下：

(28)

将式(28)代入虚拟桩法解析解(24)，便可给出桩顶嵌固情况下的解析解。取X=0(X′=(X+X0)=X0)，即可得到对于考虑表层土水平反力影响时，桩顶嵌固情况下桩顶水平位移为

(29)

同样，根据桩顶水平变位允许值χ0a，给出桩顶嵌固下的桩基水平承载力：

(30)

此外，为了便于工程设计人员在实践中应用，本文通过Matlab软件，拟合得到了桩顶自由情况下桩身弯矩最大处的无量纲深度xmax为

(31)

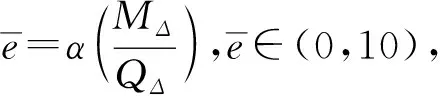
相应桩身最大弯矩为

(32)

高精度拟合公式(31)和公式(32)的最大相对误差小于1.5%，表明精度满足工程实际应用要求。

2 算例验证及计算讨论

2.1 算例1

取文献[5]中的算例。C20钢筋混凝土灌注桩，其桩径D=1.00 m，桩入土深H=10.0 m，露出地面部分的桩长为0，桩顶水平力Q0=80.0 kN，桩顶弯矩M0=150.0 kN·m，水平抗力系数m=2.00×104kN/m4，求桩顶位移y、桩顶转角φ0、最大弯矩Mmax以及最大弯矩处的相应桩深。

桩水平变形系数α=(mb/EI)0.2=0.514 0 m-1，无量纲桩长αH=5.141>4.0，可判别该桩属于柔性长桩，采用公式(26)、公式(31)等分别计算桩顶水平位移及桩身最大弯矩等，计算成果如表2所列。

表2 本文解析法与经典查表法成果对比

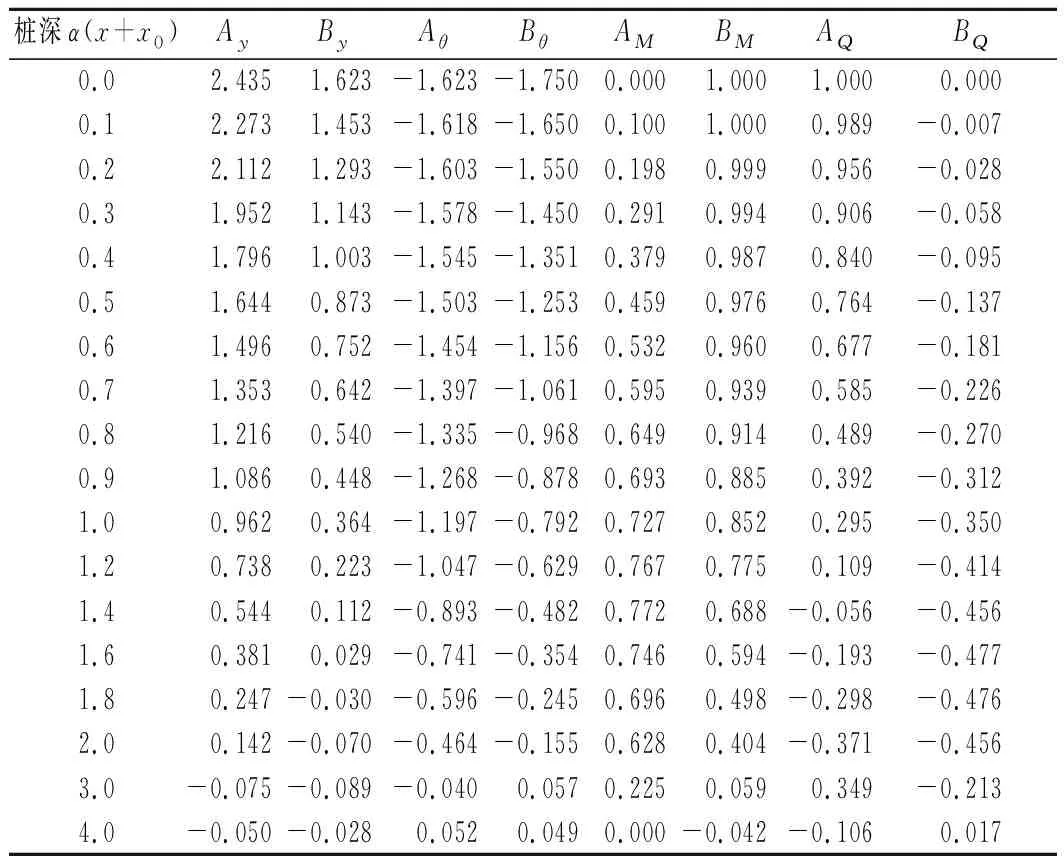
表1 柔性桩桩身水平位移等参数

由表2可以看出，本文推荐的计算公式精度可靠，而且计算过程简洁。

2.2 算例2

浙江省的一围垦工程主要建筑物由海堤、水闸等建筑物组成。海堤包括北堤、东堤和南堤，具体为：北堤长4.30 km，南堤长3.51 km，东堤长约28.85 km；水闸6座，各土层的地质参数如表3所列，其中第一层淤泥土的厚度约10 m。

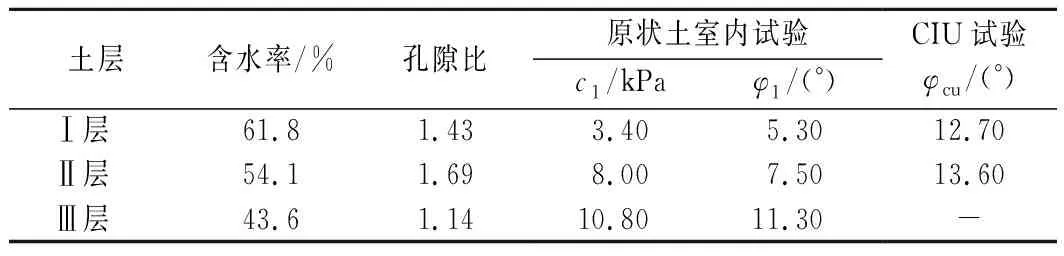
表3 原状地基土物理力学指标

钻孔灌注桩桩径为800 mm，采用C30混凝土，桩长50 m，桩身纵向配筋10φ20，Ⅲ级钢筋(见图3)；待试桩成桩1个月后进行水平承载力检测，通过埋设钢筋应力计以监测桩身弯矩。由规范[3]附录中的2(d+1)=3.6 m深度范围内，确定地基土水平反力系数的比例系数m。

图3 灌注桩水平承载力试验Fig.3 Horizontal bearing capacity test of pile

由公式(21)计算原状地基土水平抗力系数的比例系数m=0.382。

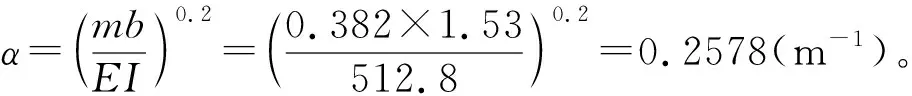
由公式(23)可得到考虑表层土水平抗力影响下的虚拟桩法参数：X0=0.259；根据表1可以计算出无量纲参数：Ay=2.012 9、By=1.205 3、AQ=0.914 2、BQ=-0.054 5、AM=0.261 5、BM=0.978 0。

根据本文新推求的承载力特征值计算公式(27)，可得RT=48.27 kN。而依据JGJ94-2008《建筑桩基技术规范》，在不考虑表层土水平抗力影响下，直接利用m值计算出的单桩水平承载力特征值Rha=26.99 kN。因此，在软土地基中桩基水平承载力计算时需考虑由黏性土黏聚力c引起的表层土水平抗力影响。

原状土中的试验桩现场水平承载力检测试验如图3(b)所示，其水平临界荷载值为60 kN；加载至120 kN时，出现第2个拐点，水平极限荷载值为120 kN。根据JGJ106-2014《建筑桩基检测技术规范》，对于桩身配筋率不小于0.65%的桩，以设计桩顶水平位移1 cm对应荷载的0.75倍作为单桩水平承载力特征值，推求得到淤泥土地基中单桩水平承载力为49.6 kN。

利用本文公式(27)推求得到水平承载力特征值为48.27 kN，与现场检测值49.6 kN接近；而采用桩基规范[3]推荐法计算得到的值为26.99 kN则偏小。因此，文中新推求的单桩水平承载力计算式实用性较好。

鉴于原状淤泥土地基中桩基水平承载力相对较低，实际工程中，可通过对原状淤泥土地基采取预压加固处理、换填硬壳层法等措施，以提高桩基水平承载力。

3 结论与建议

针对现行的JGJ94-2008《建筑桩基技术规范》中桩基水平承载力计算水平抗力系数比例系数m取值模糊、未考虑黏性土黏聚力引起的表层土水平抗力影响等问题，对桩基水平承载特性等开展了研究，可以得出以下主要结论。

(1) 根据常微分方程的幂级数解法，在考虑黏性土黏聚力c引起的表层土水平抗力影响下，通过数学推导给出了双层土地基中桩基水平承载力及变位计算解析通解。

(2) 基于新推求的通解，利用Matlab软件进行计算，给出了半刚性桩桩顶水平位移及转角的半解析计算式；同时，推导了根据地基土抗剪强度指标c、φ计算地基土水平抗力参数的解析式，进而给出柔性桩桩身任意深度处的水平位移、转角、弯矩以及剪力的解析计算式，并推求了新的桩基水平承载力计算式，同时给出了桩身最大弯矩及深度的简化公式。

(3) 作者通过工程案例，结合文中给出的计算方法，对桩基水平承载力进行了计算对比分析，并将分析结果与现场试桩的水平承载力检测值进行了验证对比。验证结果表明：本文根据地基土抗剪强度指标推求的桩基水平承载力计算方法具有较强的实际工程应用价值，最后建议软土地基中的桩基在打设前应进行软土地基预加固处理。