K&C和HJC混凝土模型在高速侵彻作用下的适用性研究

丁羽波，王 猛

(沈阳理工大学 装备工程学院，沈阳 110159)

钢筋混凝土材料凭借其承载力强、整体性好、耐腐蚀、耐高温、隔热、防辐射、可用寿命长以及成本低等优点，已经在民用建筑和军事工程等领域广泛应用[1]。随着钻地武器的快速发展，弹体高速侵彻钢筋混凝土的毁伤特性已经成为学者们关注的热点问题[2]。由于实验研究周期长、成本高，近些年数值模拟方法已成为研究高速侵彻问题的重要手段。

目前描述混凝土性质的模型有很多，如土壤/混凝土模型、K&C模型、Winfrith模型、HJC模型、CSC模型、TCK模型和RHT模型等。焦志刚等[3]基于RHT模型研究了钢筋直径和钢筋排列方式对钢筋混凝土靶抗侵彻性能的影响。马爱娥等[4]基于HJC模型和TCK模型进行二次开发，用HJC模型描述混凝土的压缩损伤行为，用TCK模型描述混凝土的拉伸损伤行为，获得了合理的混凝土损伤演化行为。孙其然等[5]基于HJC模型研究弹体侵彻钢筋混凝土时不同着靶位置对弹体剩余速度的影响规律。文献中较少研究高速侵彻条件下混凝土模型的适用性。

混凝土是典型的拉压不对称半脆性材料，现有的模型都存在一定的局限性[6]，如K&C和HJC模型均能在高速侵彻条件下使用，但具体适用于计算高速侵彻问题中的哪些参数还不明确。因此有必要研究这些模型的适用性，从而在某特定条件下选择更合适的模型。本文基于LS_DYNA动力学软件进行弹体高速侵彻钢筋混凝土靶板的数值模拟，从混凝土损伤演化，靶板开坑、崩落和弹孔破坏尺寸以及弹体贯穿靶板后的剩余速度等角度探讨K&C和HJC模型的适用性。

1 混凝土损伤模型

1.1 K&C模型

K&C模型是塑性损伤模型，考虑静水压力对混凝土损伤的影响，定义损伤方程为[7]

η(λ)=2λ/(λ+λm)

(1)

式中：λm为损伤转折点；λ为混凝土的内部损伤变量，其表达式为

(2)

(3)

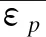
本文混凝土材料采用的K&C模型主要参数如表1所示[8]。表1中ρ为混凝土密度，v为泊松比，Rsize和UCF分别为长度单位和应力单位的换算系数，A0为单轴抗压强度，负号表示激活参数自动生成功能。

表1 K&C模型主要参数

1.2 HJC模型

HJC模型能较好地描述高应变率条件下混凝土材料的大变形问题，其损伤模型[9]通过混凝土损伤累计函数D表示为

(4)

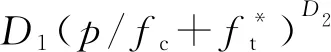
本文混凝土材料采用的HJC模型主要参数如表2所示[9]。表2中G为剪切模量，A为凝聚力强度标准值，B为压力硬化系数，C为应变率系数，N为硬化指数，ε0为参考应变率，εfmin为断裂最小塑性应变，Sfmax为最大无量纲等效应力，Pcrush为压碎应力，Ucrush为压碎体积应变，Plock为压实应力，Ulock为压实体积应变，K1、K2、K3为压力常数，Fs为失效参数。

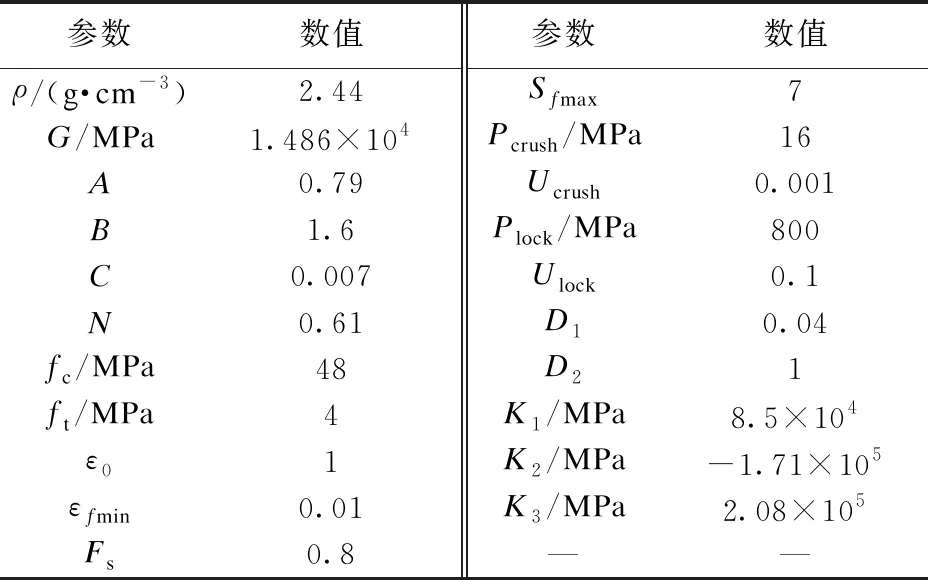
表2 HJC模型主要参数

2 弹靶侵彻数值模拟

2.1 计算模型

图1为试验中弹靶结构尺寸示意图，弹体采用4340钢，直径105mm，其他结构尺寸如图1a所示。钢筋混凝土靶板尺寸为2000mm×2000mm×180mm，钢筋网分上下两层布置，网格尺寸为200mm×200mm，钢筋层距离混凝土表面约20mm，钢筋直径为12mm，密度为7.85g/cm3，弹性模量为207GPa，屈服强度为400MPa。靶板浇筑完成后进行28天自然养护，测得混凝土抗压强度约48MPa。钢筋混凝土靶的详细结构如图1b所示。

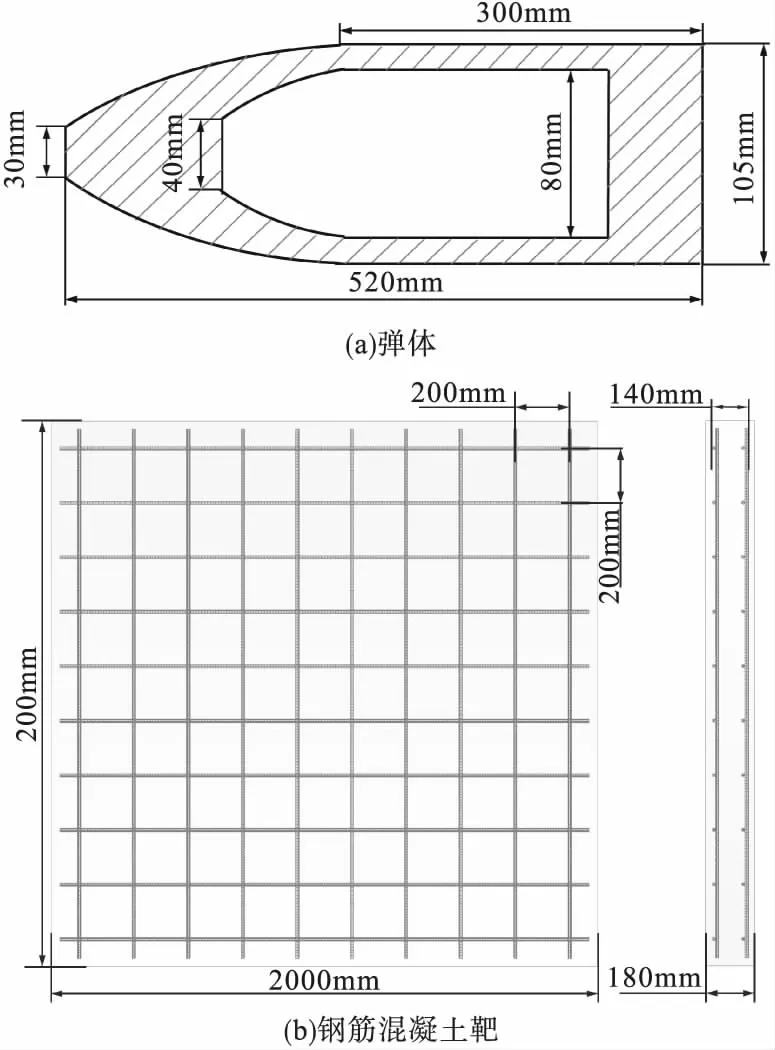
图1 弹靶结构尺寸

2.2 有限元模型

为更好地模拟靶板的动态响应、损伤行为及破坏形貌，需要考虑钢筋与混凝土的耦合作用关系，因此，本文数值模拟中建立钢筋混凝土的分离式模型。建模时，钢筋与混凝土采用不同的单元建模，混凝土采用solid 164体单元，钢筋采用梁单元，两者之间采用流固耦合关键字来设置耦合约束。

为了获得较准确的计算结果，对弹道附近的网格进行细化处理，既可提高数值模拟的求解精度，又可保证计算机的求解效率。计算模型中混凝土单元数为1166400，节点数为1212157，钢筋单元数为6596，节点数为7410，弹体单元数为9540，节点数为11963，弹靶有限元模型如图2所示。

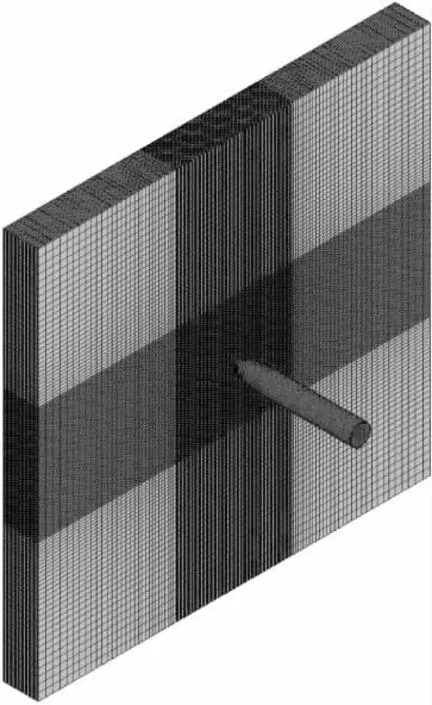
图2 弹靶有限元模型

根据靶场试验情况建立数值模型，弹体着靶速度为865m/s，且侵彻过程中弹体击中单根钢筋，着靶位置如图3所示。为防止弹体高速侵彻过程中出现单元畸变，在弹体与混凝土之间设置面面侵蚀接触，弹体与钢筋之间设置自动梁面接触，并在材料模型中考虑钢筋的失效，设定计算时间为2ms。

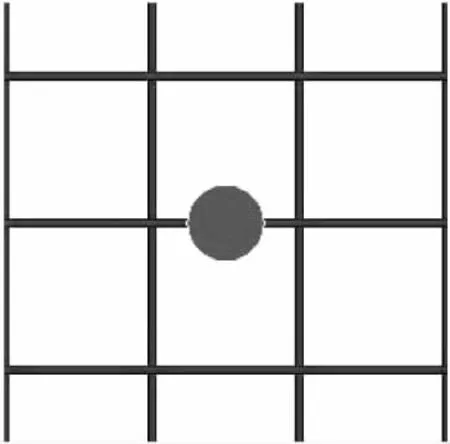
图3 着靶位置示意图

2.3 材料模型

试验中弹头部的侵蚀量非常小，可忽略不计，弹体表面仅出现轻微磨损，因此本文数值模拟不考虑弹体的侵蚀，数值模型中将弹体设为刚性材料，其参数如表3所示。钢筋采用理想弹塑性模型描述其材料行为，材料参数如表4所示。

表3 弹体材料的主要参数

表4 钢筋材料的主要参数

3 钢筋混凝土靶板毁伤特性分析

3.1 侵彻过程对比分析

为对比两种模型的侵彻过程，分别在K&C和HJC模型下，选取0.02、0.04、0.08、0.18、0.24和2ms时刻靶板的损伤云图，通过损伤演化的过程进行对比，损伤云图中由灰到黑表示混凝土的损伤程度(0～1)，颜色越深损伤越重。

3.1.1 K&C模型侵彻过程分析

基于K&C模型模拟得到不同时刻靶板的损伤变化如图4所示。

图4 K&C模型侵彻过程损伤云图

由图4可以看出，0.02ms时弹体高速撞击靶板迎弹面，混凝土材料在弹靶接触部位出现小范围的损伤，迎弹面上形成初始弹坑；0.04ms时，混凝土的损伤范围逐渐变大，弹坑进一步扩大；0.08ms时，弹体碰撞到第一层钢筋，损伤沿着第一层钢筋传播，由于在弹体的高速撞击下钢筋出现粘结滑移，钢筋滑移的同时破坏了钢筋与混凝土之间进行耦合作用的单元，对混凝土造成一定损伤，此时靶板背面也出现重度损伤，这是由于压缩波经背面自由边界反射形成了拉伸波，在拉伸波的作用下，背弹面对应位置出现损伤行为，这也间接反映了钢筋混凝土靶板背面的震塌破坏过程。随着弹体对钢筋混凝土靶的侵彻破坏，到0.18ms时，弹体撞击第二层钢筋网，此时靶板的损伤范围明显增多，背弹面呈现震塌破坏。在0.24ms时，弹体贯穿靶板形成穿孔，但靶内仍有未消散的应力波，因此应力波的后效作用依然能对靶板造成毁伤破坏。2ms时，可以看出后坑被进一步扩大，形成明显的“倒漏斗”形状，靶板四周也出现不同程度的损伤行为。

3.1.2 HJC模型侵彻过程分析

基于HJC模型模拟得到不同时刻靶板的损伤变化如图5所示。

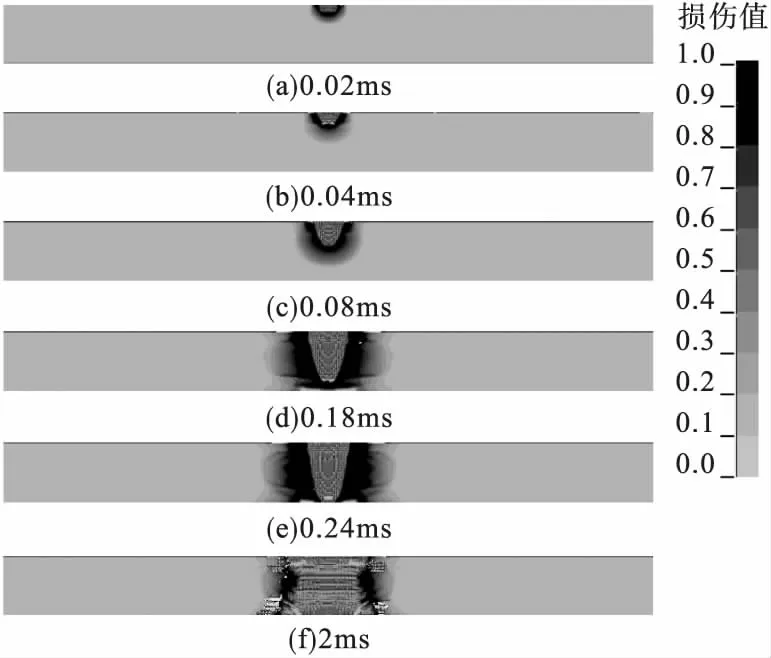
图5 HJC模型侵彻过程损伤云图

对比图5和图4可以看出，0.02ms到0.04ms时，两种模型描述的开坑损伤演化较为一致；0.08ms时，弹体击中第一层钢筋，相比K&C模型，HJC模型中既未体现钢筋处粘结破坏的损伤情况，也未出现靶板背面的拉伸损伤现象；0.18ms时，弹体击中第二层钢筋，靶板背面出现重度损伤，但仍未出现钢筋结构附近的损伤行为；2ms时，计算终止，前后坑的“漏斗”形状完全成型。HJC模型的损伤只聚集在弹孔附近，这是由于HJC模型未考虑偏应力第三不变量的影响，因此无法体现反射拉伸波对混凝土的损伤破坏。

3.2 靶板表面损伤结果对比分析

弹体高速侵彻钢筋混凝土靶板条件下，采用混凝土K&C模型模拟的迎弹面和背弹面的损伤结果如图6所示。

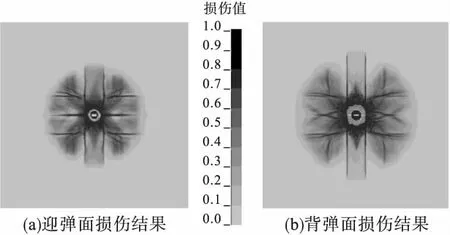
图6 K&C模型靶板表面损伤示意图

由图6可以看出，K&C模型的损伤结果近似圆形，从圆心向外由重度损伤向轻度损伤演化，其中还出现径向延伸的“线条状”重度损伤，表明该部位混凝土材料被破坏，已经失去承载能力，形成了弹坑周围径向发展的裂纹。

采用HJC模型模拟的迎弹面和背弹面的损伤结果如图7所示。

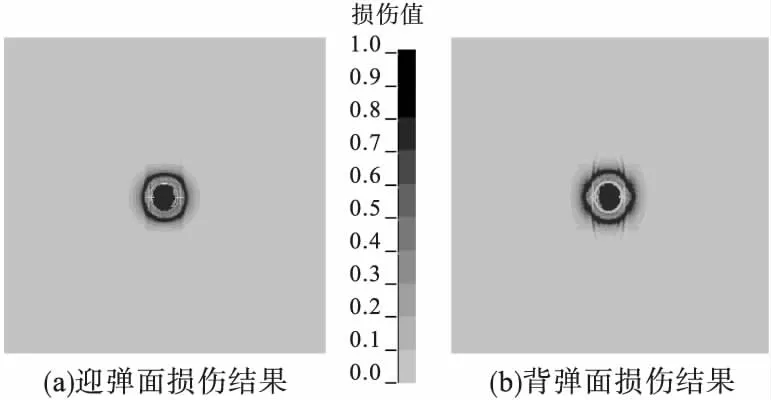
图7 HJC模型靶板表面损伤示意图

由图7可以看出，HJC模型的损伤集中在弹坑的周围，较好地体现出混凝土材料在弹体高速侵彻时的受压破坏。比较图7a和图7b，靶板表面呈现出圆形损伤，背弹面的损伤区域稍大于迎弹面，这与弹体高速侵彻钢筋混凝土靶板的试验结果相吻合。然而，HJC模型仅考虑了混凝土的压缩损伤，忽视了拉伸作用对混凝土材料的损伤行为，因此，该模型未能预测混凝土的裂纹扩展情况。

靶场试验中获得的靶板迎弹面和背弹面的破坏形貌如图8所示。试验时弹体垂直侵彻钢筋混凝土靶，着靶速度为865m/s，着靶位置为单根钢筋，靶场试验工况与数值模拟工况相同。

由图8可见，靶板的破坏不均匀，为便于比较，将开坑形状近似为圆形，测量破坏的最大和最小尺寸，并以两种尺寸的平均值作为靶板的破坏尺寸。通过试验与采用两种模型数值计算得到的靶板破坏尺寸如表5所示。

图8 试验中靶板的破坏形貌

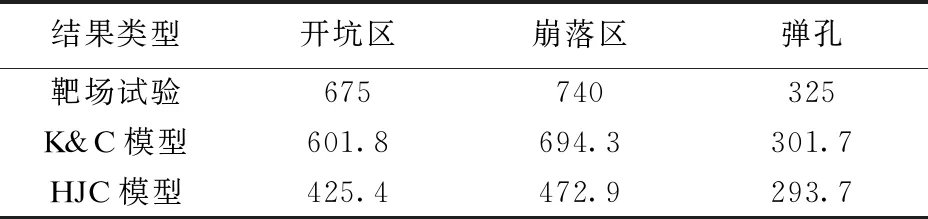
表5 试验结果与数值结果对比 mm

由表5可以看出，K&C模型模拟的开坑、崩落和弹孔尺寸较接近试验结果，而HJC模型预测的靶板开坑和崩落尺寸偏小。因此，混凝土K&C模型在模拟靶板的开坑、崩落和弹孔尺寸时更具优势。

3.3 弹体剩余速度对比分析

为对比弹体贯穿钢筋混凝土靶后的剩余速度，对文献[10]研究的不同着速条件下钢筋混凝土靶板的侵彻试验进行数值模拟，分析K&C和HJC模型模拟弹体剩余速度的适用性。

在弹体着靶速度为434、606、749和1058m/s时，分别采用K&C和HJC模型模拟得到弹体速度时程曲线如图9所示。

由图9可以看出，速度范围在434～1058m/s时，弹体的剩余速度均大于零，即该速度范围内数值模拟中的弹体均能贯穿钢筋混凝土靶板。两种模型计算得到的弹体速度变化趋势基本一致，仅在剩余速度上存在一定差别。

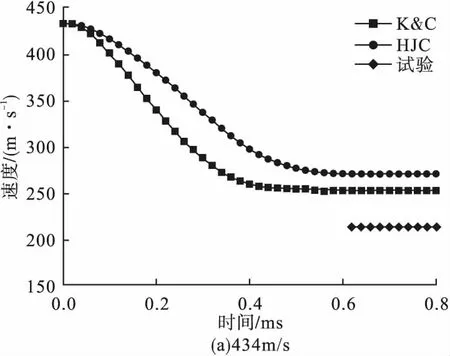
图9 不同着靶速度下弹体速度时程曲线

相同着靶速度下，通过数值模拟与试验得到的弹体剩余速度对比如表6所示。

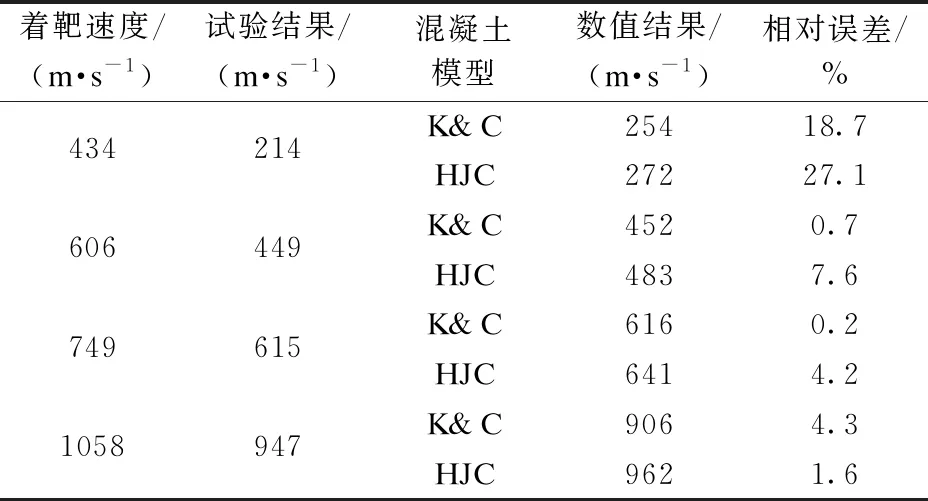
表6 弹体剩余速度对比

由表6可知，低着速时，两种模型预测的弹体剩余速度与试验结果相差较大，误差均超过10%；高着速时，弹体剩余速度的数值结果与试验结果较接近，吻合程度较高。结果表明K&C模型和HJC模型更适合在高着速条件下计算弹体剩余速度。

为研究两种模型在高着靶速度下的适用范围，绘制试验和数值计算得到的弹体着靶速度与剩余速度的关系图如图10所示。

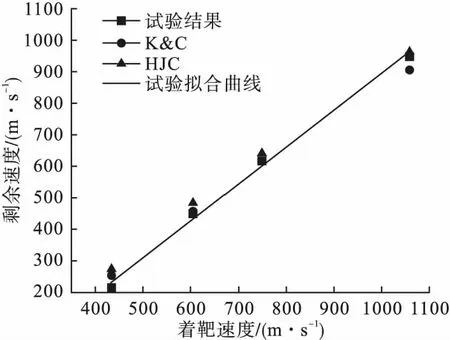
图10 弹体着靶速度与剩余速度关系

由图10可以看出：着靶速度在600～800m/s时，K&C模型计算的弹体剩余速度比HJC模型更接近试验结果；着靶速度高于800m/s时，HJC模型的计算结果更准确。

4 结论

(1)K&C模型能较好地反映混凝土的拉压损伤演化行为，且模拟的靶板开坑、崩落和弹孔尺寸比HJC模型更接近试验结果。

(2)K&C和HJC模型均可用于高着速条件下计算弹体剩余速度；HJC模型更适用于较高着速时的侵彻计算。