基于ANFIS算法的天然石材铣削加工条件下的切削载荷预测方法

2022-08-11 13:49赵德宏

沈阳建筑大学学报（自然科学版） 2022年3期

赵德宏，张帅

(沈阳建筑大学机械工程学院，辽宁沈阳 110168)

近些年研究发现，在天然大理石材料铣削加工过程中，CVD金刚石涂层刀具的使用可以明显提升加工质量。吴玉厚等[1]通过相应的铣削加工实验得出CVD金刚石涂层刀具相较于传统的未涂层硬质合金刀具具有更高的寿命和切削稳定性。闫广宇等[2]在此基础上更进一步研究，发现该刀具在切削时切削载荷相对较小，且具有更长时间的切削稳定期。赵德宏等[3]研究发现该刀具可以同时提高工艺特性和加工表面质量，并且得到相较于传统刀具，该刀具可以使切削载荷降低40%。天然石材属于硬脆材料，这就使得该石材对铣削加工中的载荷变化更加敏感。在铣削加工过程中，切削载荷与切削速度成正比，而与进给速度和背吃刀量成反比，并且在弧区范围内的影响更大。因此通过人工智能算法建立新的切削载荷预测模型，不仅可以避免这些因素对载荷的影响，而且使其硬脆性得到保护。

目前，很多学者经过实验研究，对铣削加工中的切削载荷的智能预测已经得到了众多研究成果。刘显波等[4]推导得出谐波残差的多元函数，并在此基础上得到频域多目标优化的铣削载荷预测方法。向国齐等[5]基于支持向量回归机和带精英策略的非支配排序遗传算法,通过仿真试验验证了钛合金材料Ti6Al4V的铣削加工切削载荷。杨吟飞等[6]利用传统的回归分析方法得出铣削载荷的预测模型,并通过有限元仿真进行了验证。李鑫等[7]使用神经网络算法预测铣削加工条件下的切削载荷。T.Benkedjouh等[8]以体素模型为理论基础，以有限单元法为研究方法实现了五轴铣削加工预测模型的建立。然而针对铣削加工条件下的切削载荷预测仍处于发展阶段。自适应神经模糊推理系统(ANFIS)[9]能同时发挥神经网络和模糊推理的优点，在非线性建模方面具有很好的性能，其预测的数据相较于前几种方法更具有准确性和稳定性，已经逐渐被人们接受。V.Jain等[10]使用ANFIS算法作为数学预测基础，以背吃刀量等三要素为特征输入值，可以准确预测出切削载荷数据。V.Nasir等[11]以声音信号提取特征作为补充输入值来优化ANFIS模型，使预测数据更加准确。但ANFIS模型在天然石材铣削载荷预测方面并没有过深的研究，且声音信号不能较好的表达天然石材铣削加工的特点。

鉴于上述分析,笔者在CVD金刚石涂层刀具铣削加工天然石材的工况条件下，监测出相应的振动信号，通过小波降噪方法来消除噪音等因素对振动信号的干扰，不同的特征在处理后的振动信号中被提取出来，用来优化传统的自适应神经模糊推理系统模型。研究表明：优化后的自适应神经模糊推理系统算法可以准确预测天然石材切削载荷，准确性较高。

1 实验材料与准备

选用直径8 mm的CVD金刚石涂层刀具铣削加工天然石材材料，并进行切削载荷方面的预测。在实验中，三个不同的转速(4 300、5 200和6 000 r/min)，进给速度(800、1 200和1 500 m / min)和三个级别的切削深度(6、8和10 mm)进行实验，设计27组不同的实验加工处理方式。使用EMX09测振仪测量出相对应的27组振动信号如图1所示，用于以后的实验分析与优化。使用9257B测力仪测量出相对应的27组切削载荷数据，如图2所示，用于以后的实验验证与数据对比。

图1 EMX09测振仪检测信号

图2 测力仪测量切削载荷数据

2 小波降噪处理及特征提取

图3所示为第1种方案(转速4 300 r/min，进给速度800 m/min，背吃刀量6 mm)的时域信号。一般情况下获得的振动时域信号通常被噪声干扰[18]，因此，信号去噪声处理过程是不可避免的。近几年来，该理论[20]在学术界得到了普遍认可，应用范围也越来越广泛。在去噪领域中也获得相似的认可，使用该方法进行去噪处理也越来越成为一种趋势。

图3 第1种方案的时域信号

函数逼近是该理论的核心问题和研究重点，即如何在由小波母函数伸缩和平移版本所展成的函数空间中，以衡量准则作为该理论的基础，找出与原信号最相近的信号，以完成原信号和噪声信号的区分。该理论的特点就在于其对频率区间的局部化分析，它通过伸缩平移运算对信号(函数)逐步进行多尺度细化，最后完成高频信号和低频信号的区分，以满足对时域信号自动适应的任务，从而实现噪声信号和实验所需的时域信号分别提取，来进行后续的快速傅里叶方法使用和频域信号转换。小波降噪理论的具体流程如图4所示。

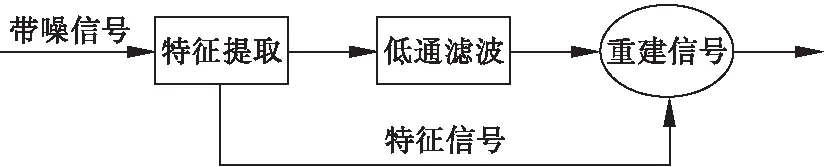
图4 小波降噪方法处理流程

该理论的处理流程：

(1)对输入信号进行小波分解，得到高频分量和低频分量；

(2)对高频分量进行阈值处理；

(3)重新构建进行阈值处理后的分量，得到去噪后的信号。

运用Matlab中的wavelet de-nosing method函数来实现小波降噪的方法，去噪后的时域信号函数如图5中的实线所示，大大降低了噪声对振动时域信号的影响，进而可以保证信号的稳定性和准确性。经过小波降噪处理后得到稳定的时域信号，再使用快速傅立叶变换算法将时域信号转换成实验所需的频域信号。再从频域信号中提取5个重要的特征[19](偏度、峰度、香农熵、标准差和均方根)用于代表电主轴振动信号，提取特征的具体数学表达方法如表1所示。

图5 第1种方案时域信号的小波降噪处理

表1 特征的数学公式

3 自适应神经模糊推理系统理论基础

自适应神经模糊推理系统算法(Adaptive Neuro-Fuzzy Inference System，ANFIS)是一种以人工智能方法(Takagi-Sugeno)为理论基础的推理模型，ANFIS使用传统的神经网络方法来实现，包括反模、模糊推理和反模糊化三个基本步骤[13]。

ANFIS算法在传统的神经网络算法的基础上添加了模糊处理，进而生成了自适应神经模糊推理器，通过机器学习方法和自学习系统来进行该推力器的控制和调整，实现了两种算法：神经网络和模糊推理的相辅相成[12]。从而实现模仿人脑系统进行研究数据的智能预测，最大程度上减小了预测误差，提高了预测精度。模糊推理的规则如以下两个公式，并在此基础上通过神经网络对实验数据进行模拟和训练。

ifXisX1 andYisY1

执行库存管理｜出库业务｜销售出库，单选择2018年1月5日信息，生成销售出库单，并完成审核。特别提示：如果同一批次销售不同仓库的商品，在生成销售出库单时，可以选择生单按钮下拉列表中的“销售生单（批量）”命令，这样可以一次生成不同仓库的多张出库单。

f1=p1X+q1Y+r1.

(1)

ifXisX2 andYisY2

f2=p2X+q2Y+r2.

(2)

其中，p、q和r是预测实验中特定的参数[15]，输入节点代表实验的训练数值。输出节点代表实验预测值。而隐含层中包括实验所需的隶属度函数(MFs)和相应的功能节点[17]。与模糊推理(FIS)的架构相似，ANFIS算法的架构中也包括输入函数的模糊化，模糊规则推理和火力计算(蕴含)，输出函数去模糊化的基本流程。ANFIS模型的模糊推理步骤如图6所示。

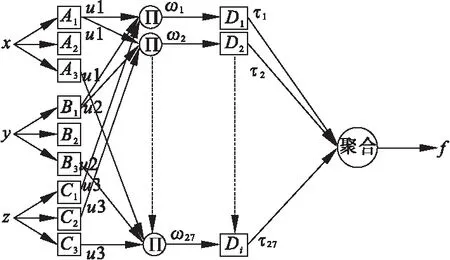
图6 自适应神经模糊推理系统基本框架

ANFIS算法的基本框架中，位于第一层的自适应节点被普遍命名为前提参数，来对输入函数MF进行处理。

Q1,i=μAi(x),i=1,2.

(3)

Q2,i=μBi(y),i=1,2.

(4)

式中：x和y是节点i的输入，Ai和Bi是预测模型的标签，而ua和ub则属于隶属函数[16]。ANFIS模型可以选取不同的隶属函数。高斯隶属度函数可以对生成时间和处理时间进行非线性处理，因而该隶属度函数应用范围较广，可以保证函数的稳定预测。高斯隶属度函数的具体数学表达方法如下:

(5)

(6)

式中：ai1,ai2,bi1和bi2是参数集[14]。

(7)

第三层和第四层的表达方法如下:

(8)

(9)

其中,第三层代表触发强度，第四层代表结果参数。

f1和f2符合下面公式中的模糊推理规则：

ifXisA1 andYisB1

f1=p1X+q1Y+r1.

(10)

ifXisA2 andYisB2

f2=p2X+q2Y+r2.

(11)

其中,wi代表该层的统一发射强度，[pi，qi，ri]仍然是参数集，并且也可以作为后续参数。

在第五层中，通过对模糊化处理过的函数进行输出求和，得到如下结构：

Q5,i=fout=∑wi×fi=overall output.

(12)

在该自适应神经模糊推理系统算法的框架中，第一层和第四层都具有不同的自适应节点。在第一层中，有两个可修改的前提参数，在第四层中，除了这两个前提参数之外，还具有一个可修改的后继参数[pi，qi，ri]。ANFIS模型预测切削载荷的具体步骤如图7所示。

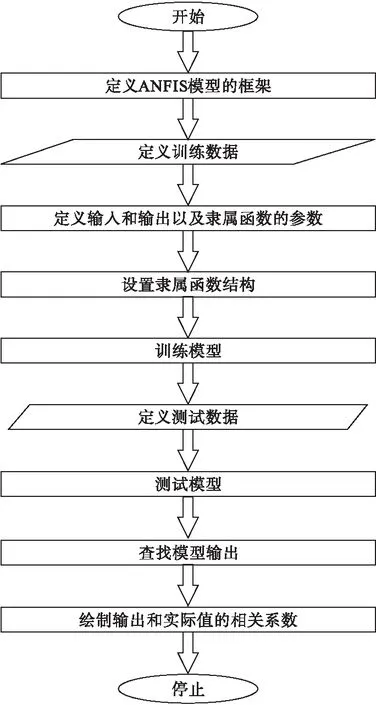
图7 自适应神经模糊推理系统操作步骤

从自适应神经模糊推理系统算法的框架中可以得出：一般情况下，如果输入值越多，那么该算法最终得到的预测数据精度也越高，不过伴随着太多的输入量，也会生成不必要的预测网络，不仅无法达到提高预测精度的效果，反而会使造成不必要的浪费，导致模型崩溃，使得预测精度不会有太大的提升。从理论层面，把从电主轴振动信号中提取的特征作为补充输入量，可以增加ANFIS模型预测数据的准确性，但应该合理地控制输入量，所以笔者主要提取了5个重要特征。

4 实验结果与讨论

笔者通过实验生成了2种ANFIS模型，第一个传统的预测模型是使用切削三要素(进给速度、旋转速度、背吃刀量)作为输入量，第二个ANFIS模型是同时使用切削要素和经过小波降噪处理后，从电主轴振动信号中提取的特征同时作为输入量的新的预测模型如图8所示。首先在Matlab中导入相应的大量训练数据，训练数据用于检测模型构建和评估模型的准确率。

图8 两种切削载荷预测模型

参数估计值与参数实际值在预测分析过程中具有重要地位。通过比较两种模型训练数据的相关系数MSE和均方误差R2来初步得到结论，如表2所示。

表2 ANFIS模型实验结果

从表2可以看出，两种模型都具有很好的预测性能，同时第二种模型也就是优化后的模型均方误差更小，使预测数据的准确性和稳定性越高，同时相关系数绝对值更接近于1，说明线性相关性越强，上下波动越小，通过训练数据的分析，可以初步得到结论，两种模型都具有很好的预测性能，并且优化后的模型具有更好的预测性能。最后导入本次实验中的实际测试数据，预测结果如表2所示，实际测试数据的模糊规则观察模块和输出曲面观察模块如图9所示，可以准确地得到输入量(切削速度、进给速度、背吃刀量)与输出量(切削载荷)之间的关系。

图9 测试数据的模糊规则观察和输出曲面观察

比较两组模型的切削载荷预测值与实际测量值之间的误差如表3所示。可以看出，两种模型都具有很好的预测性能，第二种模型的测试数据的均方误差更小，同时相关系数绝对值更接近于1，其具有更好的性能。该方法能够使切削载荷预测准确性达到92%，相对于传统模型具有更好的预测精度，达到了优化传统预测模型的效果。

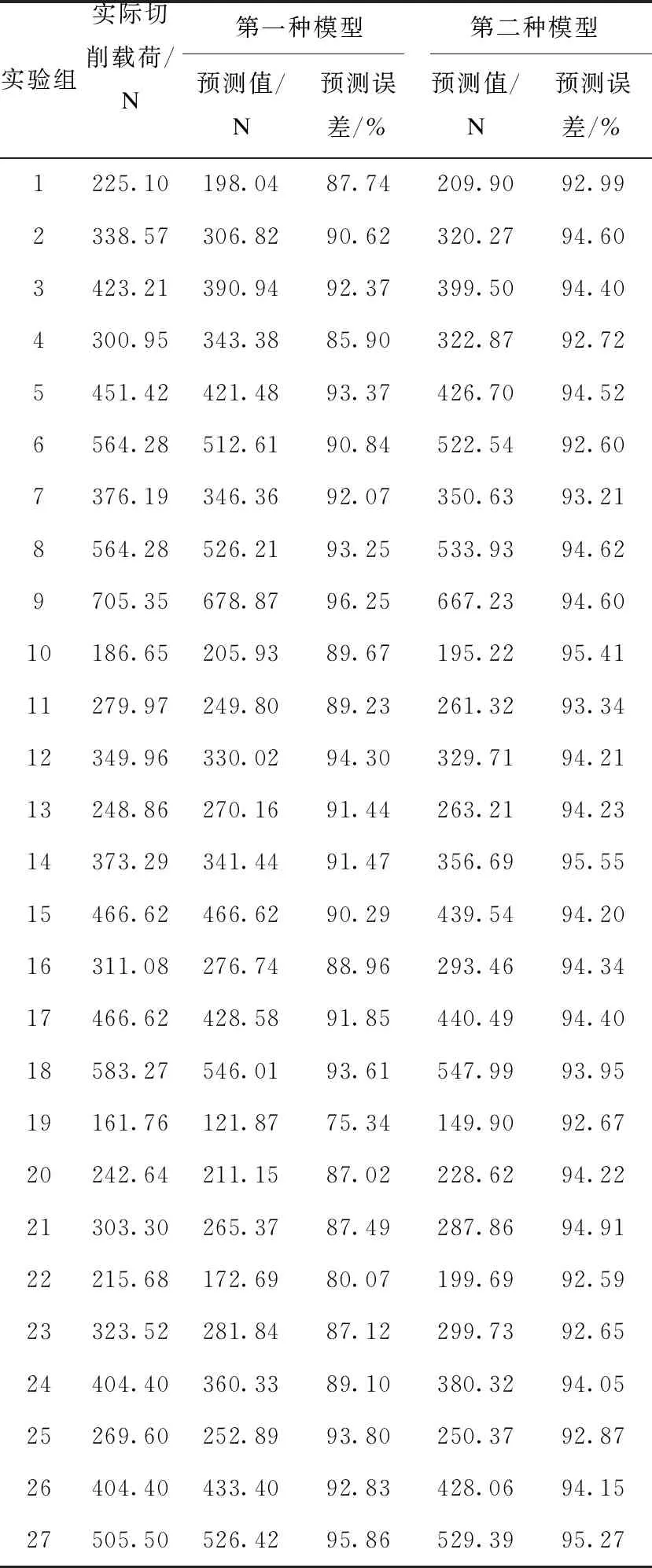
表3 铣削载荷预测结果

5 结论

(1)针对CVD金刚石涂层刀具铣削加工天然石材条件下的切削载荷预测问题，笔者建立了自适应神经模糊推理系统模型，并采用小波降噪的方法从处理后的振动信号中提取出了重要特征，优化了传统的ANFIS模型。

(2)优化后的ANFIS模型具有更好的预测性能，其充分运用了天然石材铣削工况下的加工特征，提高了预测模型的预测精度。