λ噬菌体阻抑物基因表达调控的随机稳态结构

黄婷,张宇欣,唐伟,游雄*

(1.南京农业大学园艺学院,江苏 南京 210095;2.南京农业大学理学院,江苏 南京 210095)

λ 噬菌体是一种感染大肠杆菌的病毒。λ噬菌体感染宿主大肠杆菌细胞后,进入2个不同的生命周期:裂解周期或溶原周期。裂解生长(lysis)的噬菌体,通过感染宿主复制自身的DNA,并合成外壳蛋白,产生大量的子代噬菌体,通过宿主细胞的裂解释放出来。溶原生长(lysogeny)的噬菌体,将自身的DNA熔合到宿主细胞的染色体中,通过细菌分裂实现复制。λ 噬菌体的基因组只有50 kb,包含50个基因,其中大部分编码裂解蛋白、外壳蛋白、重组蛋白和参与DNA复制。在这2个不同的生命周期中,调控基因cI有不同的表达模式。λ 噬菌体的基因组调控机制相对简单,成为应用数学模型方法分析基因调控网络动力学的典型案例之一[1-2]。

阻抑物CI蛋白的负反馈自调控在λ噬菌体发育周期中起着重要作用[3]。Ptashne等[4]和 Johnson等[5]确定了λ 噬菌体lysis-lysogeny通路中基因调控表达机制。λ噬菌体基因表达调控的DNA序列包括 2个主要基因cI和cro,3个启动子PR、PL(分别表示右向和左向启动子)和PRM(CI蛋白维持启动子)。cI基因编码 λ 阻抑物CI蛋白。在λ噬菌体内,CI蛋白与早期转录启动子PR和PL以分离或结合的动态平衡控制噬菌体的溶原或裂解途径[6]。大多数噬菌体基因的转录直接或间接受到PR和PL的调控。PRM是维持阻抑物CI蛋白的启动子,并且只转录cI基因。当PRM处于关闭状态且PR和PL处于开放状态时,细菌处于裂解生长周期;当PRM处于开放状态且PR和PL处于关闭状态时,细菌处于溶原生长周期。这些启动子的活性受6个操纵子的调控[7],其中左右控制区各分3个位点,两侧无论是作用位点序列还是结合模式都相似。右侧启动子PR有3个操纵子位点OR1、OR2和OR3,其中OR1与PR重叠,OR3与PRM重叠[8-9]。

Hasty等[10]建立了一个λ 噬菌体阻抑物基因表达的确定性微分方程模型,对微分方程的分支分析结果解释了被感染细菌的溶原生长和裂解生长。然而,由于转录、翻译和翻译后蛋白修饰过程所涉及的少数分子的离散特点,基因表达过程本质上具有随机性。这种随机性可能引起生物发生表型变化[11],也是导致细胞分化和机体发育的机制之一[12]。

本文研究 λ 噬菌体cI基因随机表达调控的动力学。按照阻抑物CI蛋白的线性降解和非线性降解 2种情形,分别建立化学主方程[13]。通过蒙特卡洛模拟[14-15],观察不同降解率常数下基因调控的稳态结构,探究 λ 噬菌体侵染的大肠杆菌不同生长状态及其切换的机制。

1 模型与方法

1.1 λ 阻抑物自调控模型

本文考虑λ 噬菌体的一种不含位点OR1的突变体[16]。基因cI编码阻抑物CI蛋白,阻抑物CI蛋白二聚化,然后结合到位点OR2或OR3上。当二聚体结合到OR2上时,基因表达增强,并且屏蔽位点OR3的作用;当OR3上有二聚体结合时,基因表达受到抑制(停止)。图1为λ 噬菌体阻抑物CI 蛋白反应通路模型。该通路的化学反应包括4类。

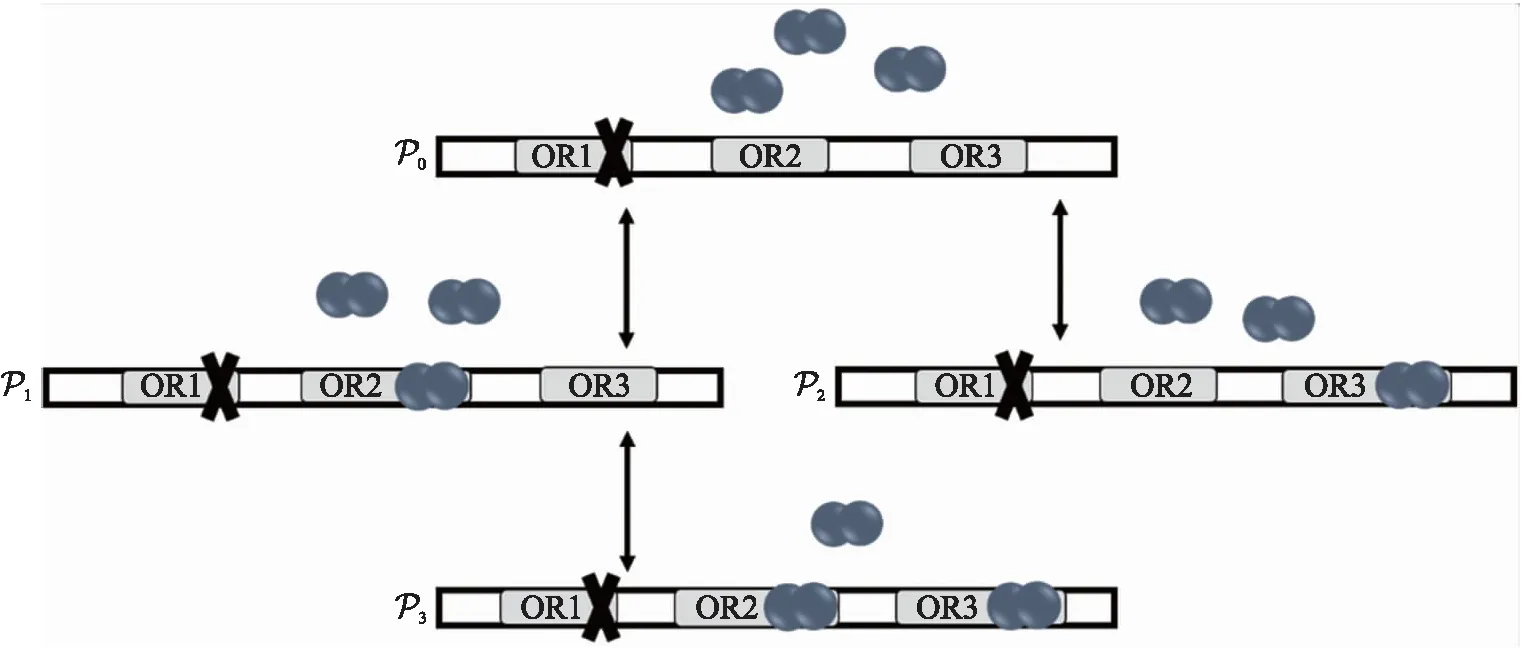
图1 λ 噬菌体cI基因自调控表达Fig.1 Self-regulated expression of the cI gene in λ phage表示启动子上未结合二聚体;表示位点OR2上有二聚体结合;表示二聚体结合到位点OR3上;表示位点OR2和OR3上都有二聚体结合。当二聚体结合到OR2上时,基因表达增强;当OR3上有二聚体结合时,基因表达停止。OR1、OR2、OR3分别为启动子PR的3个不同的操纵子位点。 indicates that the dimer is bound to the site indicates the sites OR2 and OR3 both have dimer binding. When only a dimer binds to OR2,gene expression is enhanced;when a dimer binds to OR3,gene expression stops. OR1,OR2 and OR3 are three operon sites of promoter PR,respectively.

1)阻抑物CI蛋白的二聚化和二聚体的分解

(1)

式中:Λ为蛋白单体二聚化的反应速率常数;θ为无量纲平衡解离常数。

2)操纵子状态的转换

(2)

(3)

(4)

式中:K1、K2、K3为二聚体与2个操纵子OR2、OR3结合的正向反应速率常数;β1、β2、β3分别是这3个反应的无量纲解离常数。

3)cI基因表达(CI蛋白的生成)

(5)

(6)

式中:蛋白生成速率α0、α1依赖于操纵子的化学状态。需要注意的是,这2个简单的反应式代表了大量的有效反应,包括cI基因的转录、mRNA 到多肽的翻译以及这些多肽向蛋白的折叠。

4)阻抑物 CI蛋白的降解

蛋白丰度的相对稳定对于被λ噬菌体侵染的大肠杆菌的正常运行至关重要。细胞通过平衡合成和降解的过程,让蛋白丰度维持在适当水平,使λ噬菌体处于相应的生长周期,同时通过打破这种平衡来实现不同生长周期的过渡。蛋白的降解是一个重要的调节机制。蛋白的降解速率对基因调控系统的动力学行为具有重要影响。蛋白的降解速率还与细胞的营养状况和激素水平有关。例如,在营养缺乏的条件下,细胞加速蛋白的降解,以便为必不可少的代谢过程提供重要的营养。

真核生物中,蛋白的降解有两种体系:一是由溶酶体负责的蛋白降解,二是依赖ATP的泛素-蛋白酶体系统(ubiquitin-proteasome system,UPS)。2008年Pearce 等[17]在结核分枝杆菌中发现了原核类泛素蛋白(prokaryotic ubiquitin-like protein,Pup)。Pup在辅助因子的作用下标记多种功能蛋白,并介导被标记蛋白通过蛋白酶体降解。研究表明,蛋白的降解速率与蛋白丰度存在依赖关系[18-19]。在数学模型中反映这种依赖性的方式有2种动力学:质量作用定律(线性降解)和Michaelis-Menten(MM)动力学(非线性降解)。MM动力学可以刻画蛋白经由“Pup-蛋白酶体”通路降解过程的复杂性。为简单起见,假设二聚体不降解,也就是,只有蛋白的单体形式是不稳定的。蛋白单体的线性降解的反应表示为:

(7)

式中:δ为降解速率常数;φ为蛋白的降解产物。

基于MM动力学的蛋白单体非线性降解的反应表示为:

(8)

式中:M为蛋白单体的数量;KI为蛋白单体半数最大有效丰度,称为MM常数。

阻抑物CI蛋白线性降解假设下的速率方程及其分支分析见文献[10]。CI蛋白非线性降解情形的无量纲化方程为:

(9)

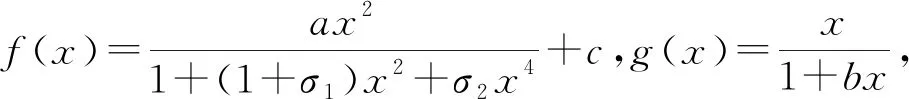
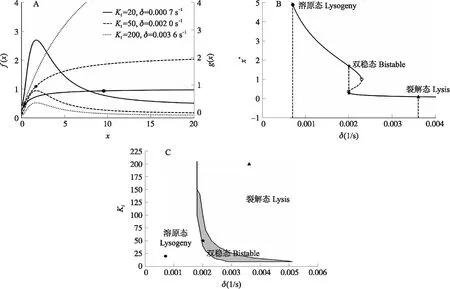
图2 λ阻抑物基因反应通路确定性模型的分支图Fig.2 Bifurcation analysis of a deterministic model of the repressor in λ phage a λ inhibitor gene A. 函数f(x)、g(x)和x的双纵坐标图像;B. 系统平衡态x*与降解速率δ的关系(KI=50)。实线表示平衡点是稳定的,虚线表示平衡点不稳定,圆点“o”对应鞍结点分支;C. δ-KI平面分支图。其他参数取自文献[10,20]。A. Bicoordinate diagram of functions f(x),g(x)against x;B. The relationship between the equilibrium x* of the system and the degradation rate δ(KI=50). The solid line indicates that the equilibrium is stable,the dotted line represents that the equilibrium is unstable,and the dot “o”corresponds to the bifurcation of the saddle node;C. Bifurcation diagram in the δ-KI plane. The other parameters are taken from references[10,20].

1.2 化学主方程

Hasty等[10]通过在方程(9)中引入加性噪声,得到Langevin方程。利用Langevin方程研究外噪声如何控制细菌的动力学行为。本文考虑基因的随机表达,探讨分子噪声诱导细菌选择生长周期。

1.2.1 阻抑物蛋白线性降解在任意给定时刻t,cI基因自调控网络的状态由单体蛋白的数量M(t)和启动子的化学状态S(t)确定。如果操纵子OR2和OR3未被占用,则S(t)=0;如果OR2与二聚体结合,则S(t)=1;如果OR3与二聚体结合,则S(t)=2;如果OR2和OR3都与二聚体结合,则S(t)=3。因此,系统的各种状态取值可以写成有序数对(m,s),其中m是非负整数,s取0、1、2、3。

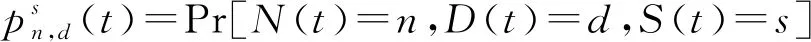
(10)

(11)

(12)

(13)

式(10)—(13)中每一个方程右端第1项表示由于单体蛋白生成使得系统状态变为(n,d,s)时的净概率流;第2项表示由于蛋白质单体降解使得系统状态变为(n,d,s)时的净概率流;第3项表示单体生成二聚体使得系统状态变为(n,d,s)时的净概率流;第4项表示由于二聚体分解为单体使得系统状态变为 (n,d,s)时的净概率流。含有Ki的项表示由于二聚体与启动子结合或解离使得系统状态变为(n,d,s)的净概率流。式(12)—(13)的右端没有蛋白生成的概率流。所有参数均表示随机反应速率常数。

主方程(10)—(13)也可以写成下列紧凑方程:

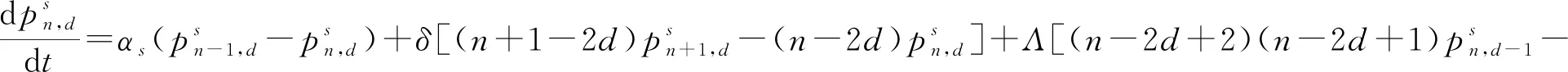
(14)

式中:n=0,1,…;d=0,1,…,[n/2]([n/2]表示n/2的整数部分);s=1,2,3,且当s=2,3 时,αs=0。

1.2.2 阻抑物蛋白非线性降解如果蛋白的降解服从MM动力学,那么cI基因网络的化学主方程为:

(15)

式中:n=0,1,…;d=0,1,…,[n/2]([n/2]表示n/2的整数部分);s=1,2,3,且当s=2,3时αs=0。

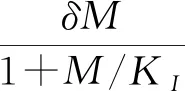
2 结果与分析

在感染了噬菌体的细菌中,CI蛋白的数量作为细菌状态的指示器。CI蛋白高表达,系统处于溶原生长周期;由于某种原因CI蛋白的拷贝数变得很少,则系统转向裂解周期[7,20]。酶的活性会受到温度、pH值以及细胞质中其他小分子的影响,公式(7)—(8)中的常数δ、KI会在一定的范围内变化。我们借助参数δ、KI,通过蒙特卡洛模拟观察CI蛋白的不同降解方式和降解速率对 λ 噬菌体基因调控系统稳态的影响,探索系统对2种生长周期的选择倾向性。

Cao等[20]研究发现,当CI蛋白的降解速率为0.000 7 s-1时,CI蛋白拷贝数高。当CI蛋白的降解速率从0.000 7 s-1增加到0.002 s-1时,即λ噬菌体被诱导到裂解态前,处于溶原态和裂解态的过渡阶段,CI蛋白数量呈现双峰稳态分布。当CI以较快的速率(δ=0.003 6 s-1)降解时,CI拷贝数接近0,对应于λ噬菌体的裂解态。

2.1 线性降解下λ噬菌体的状态实现

我们首先对线性降解方程(14)应用蒙特卡洛模拟。参照Cao等[20]研究结果,除了δ和KI外,其他参数取值为θ=2.364 6,Λ=0.422 9 s-1,α0=0.006 9 s-1,α1=0.066 s-1,K1=0.021 s-1,K2=0.021 s-1,K3=0.021 s-1,β1=0.08,β2=0.08,β3=5。

依次采取低降解速率δ=0.000 7 s-1,中等降解速率δ=0.002 s-1和高降解速率δ=0.003 6 s-1,对方程(14)应用蒙特卡洛模拟。从图3可知:对低降解速率δ=0.000 7 s-1,CI蛋白表达处于较高水平,呈单峰稳态分布,与溶原态基本一致(图3-A、B);对中等降解速率δ=0.002 s-1,CI蛋白数量在20～50无规则波动,没有呈现双峰分布,与试验中观察到的双稳态切换不符合(图3-C、D);而在高降解速率下δ=0.003 6 s-1,CI处于稳定的低表达状态,与裂解态基本一致(图3-E、F)。上述结果表明,线性降解模型(14)不能正确表现λ噬菌体的溶原态和裂解态之间的双稳态切换机制。

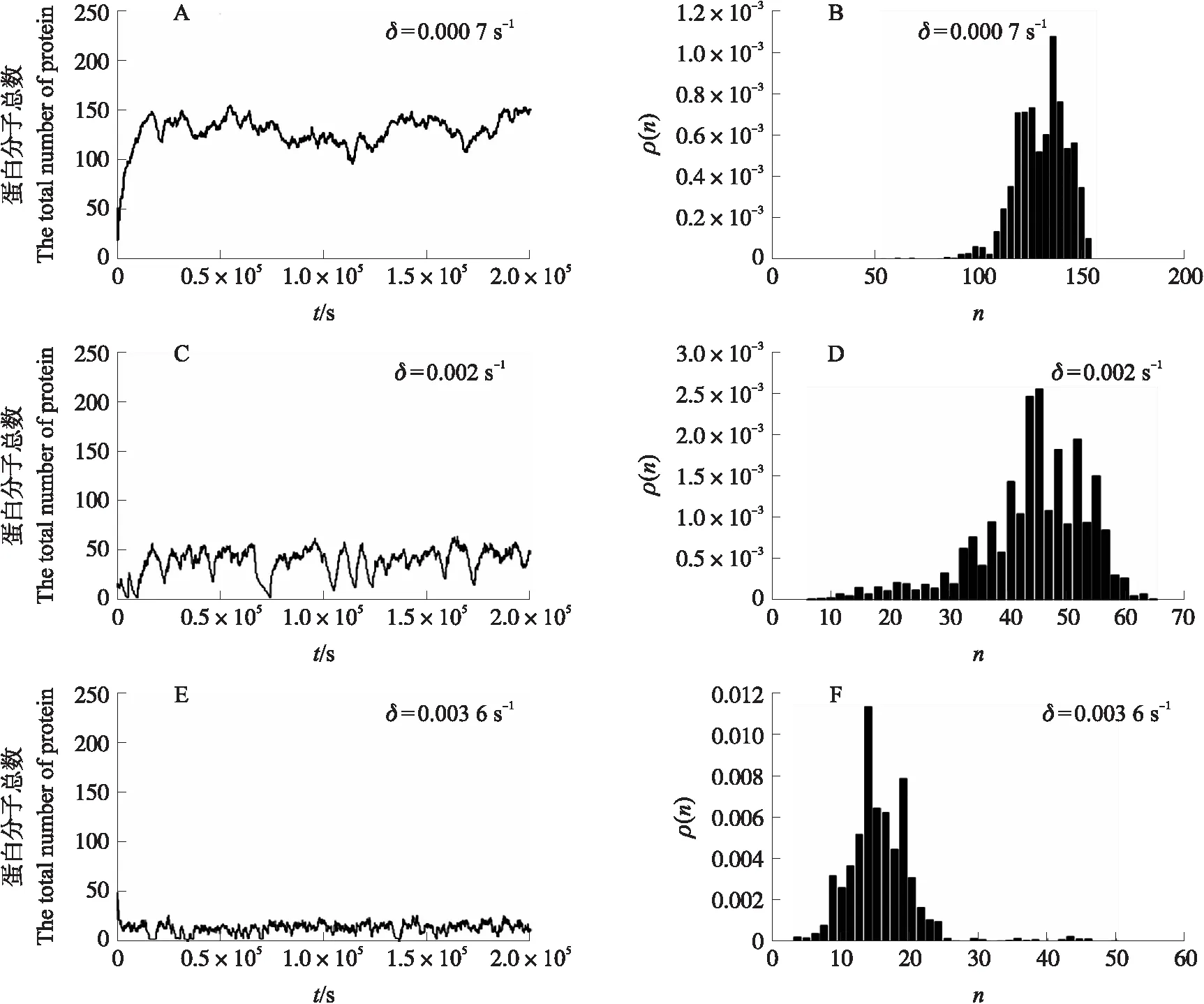
图3 线性降解下CI蛋白的样本路径和稳态分布Fig.3 Sample paths and steady-state distributions for CI protein with linear degradation

2.2 非线性降解下λ噬菌体的状态实现

除了δ和KI之外,其他参数与线性降解情况相同。为了实现λ噬菌体的溶原态、双稳态和裂解态,对降解率δ的3个不同取值(0.000 7、0.002和0.003 6 s-1)根据图2-C稳态区域划分,分别取半数最大有效丰度KI=20、50和200。从图4可知:当δ=0.000 7 s-1时,λ噬菌体内阻抑物CI蛋白持续保持较高丰度(>100),呈现单峰稳态分布,此时cI基因表达水平较高,细胞处于稳定的溶原周期(图4-A、B);当δ增加至 0.002 s-1时,CI蛋白的丰度在2个稳态水平上交替跳转,呈现双峰分布,细胞在溶原态和裂解态之间反复切换(图4-C、D);当δ增加至 0.003 6 s-1时,CI蛋白丰度急剧下降至极低水平,呈单峰稳态分布,细胞进入稳定的裂解生长周期(图4-E、F)。上述结果表明,非线性降解模型(15)完整正确地表现了λ噬菌体的随机稳态结构。

进一步的模拟显示,当蛋白降解速率继续增加(如δ>0.1),线性降解模型和非线性降解模拟的结果没有明显差别,CI蛋白数量非常稳定地处在极低水平,细胞长期处于稳定的裂解周期。这表明如果CI蛋白的降解速率超过一定的阈值,降解方式不影响系统状态。

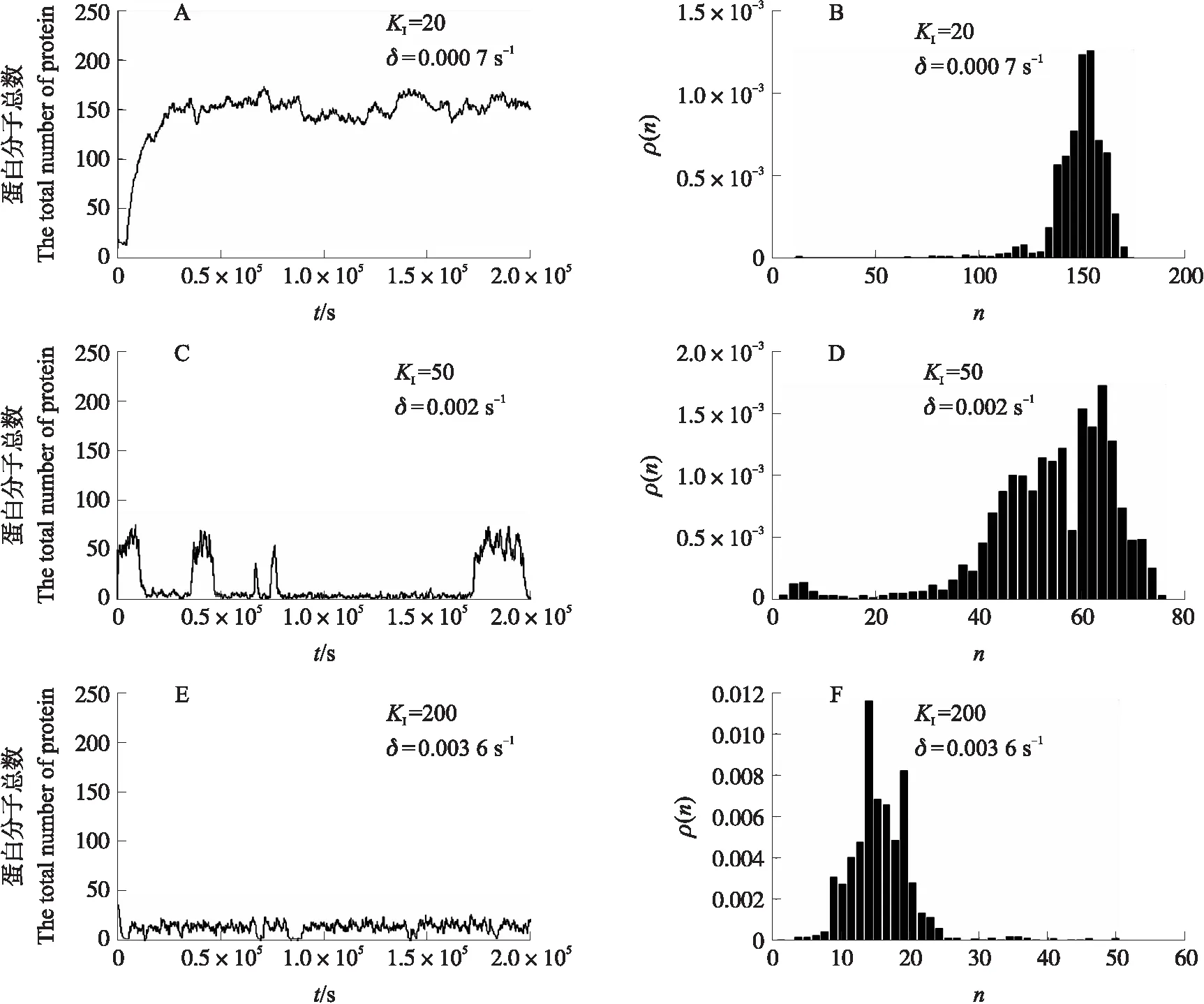
图4 非线性降解下CI蛋白的样本路径和稳态分布Fig.4 Sample paths and steady-state distributions for CI protein with nonlinear degradation

3 结论

本文研究 λ 噬菌体侵染大肠杆菌中自阻抑物CI蛋白的降解方式对基因表达稳态结构的影响,建立cI基因调控网络的化学主方程,其中考虑了蛋白线性降解和非线性降解两种情况。蒙特卡洛模拟结果表明,与线性降解模型相比,非线性降解模型更为准确地刻画λ噬菌体内分子噪声的随机动力学。

本文发现噬菌体命运决定的一种新机制:阻抑物蛋白CI的降解率及降解方式。λ 噬菌体为了决定溶原/裂解态,必须选择与降解率δ相匹配的半数最大有效丰度KI。降解率较高时,CI蛋白倾向于线性降解,细菌更容易进入裂解周期;降解率较低或很低时,CI蛋白倾向于非线性降解。降解率δ越小,半数最大有效丰度KI值也越小,降解的非线性越强,细菌更容易进入溶原周期。

本文数学模型与随机模拟方法也可以应用于真核细胞中通过其他转录因子或染色质-DNA相互作用调节基因表达的系统。