基于智能体的无人机集群弹性均衡度量与仿真评估方法

周国强，穆 琳，吴家仁，潘 翼，海星朔，高济禾

(1.航空工业 沈阳飞机设计研究所，沈阳 110035； 2. 北京航空航天大学 可靠性与系统工程学院，北京 100083)

0 引 言

随着智能化战争环境日趋复杂，无人机(Unmanned Aerial Vehicles, UAV)集群在任务执行过程中可能面临持续外部破坏，包括连续极端恶劣天气或敌方蓄意攻击等，将造成无人机集群部分功能失效、通讯中断甚至整机损毁等问题，严重影响整体任务执行。

为反映集群对破坏事件的承受和恢复能力，国内外学者将“弹性”概念应用到无人机集群的研究中。Bai等提出一种基于当前性能与标准性能差异的改进弹性度量，以反映无人机集群适应破坏性事件和恢复其预期性能的能力。Ordoukhanian等基于仿真方法建立动态效用函数，并对无人机集群任务执行期间的性能备选方案进行实时评估，以此建立无人机集群弹性。Feng等针对无人机编队在随机攻击下的快速重构问题，提出一种编队弹性度量与优化方法，并通过仿真实例验证了方法的有效性和快速性。

弹性来源于对系统设计中赋予其内部各要素的冗余能力。因此，相比于抗毁性、鲁棒性、可靠性等指标，弹性可对无人机集群抵御破坏能力进行全面评估。然而，面对集群可能遭受的持续性破坏，要求各飞行编队都应具备一定的冗余，也可以说具备一定“弹性”。当前，表征此类特征的相关度量方法研究较少，故本文重点在于提出一种能够反映集群各组成部分剩余能力均衡特征的度量指标。

智能体被定义为能够在某一环境中与其他个体进行互动、协调以实现特定目标的自治软件实体。基于智能体的建模(Agent-Based Modeling, ABM)方法可以在人工环境中对真实场景中的复杂实体关系进行模拟，因其具有典型的协作性、并行性、鲁棒性、易扩展性等特征，已被广泛应用于无人机集群建模。例如，Zou等提出一种基于ABM方法和多目标优化的多无人机冲突解决方法， 使用参数化的几何表示描述了三维空间中无人机碰撞行为。文献[13-14]等利用ABM方法分别对无人机集群的自主任务管理和任务规划进行设计。尽管国内外研究人员通过ABM方法对无人机集群进行了深入分析，但以上方法在实现任务执行、破坏以及重构建模方面还存在一定不足。

本文针对无人机集群遭受破坏后的剩余能力均衡问题，提出一种持续破坏下无人机集群弹性均衡度量与仿真评估方法，为集群持续破坏下的能力设计提供支撑。

1 面向任务的集群弹性均衡度量

1.1 基本定义

将任务空间∈内的无人机集群记为={,, …,}，其中，为集群规模，∈。对于集群中的每架无人机，∈{1, 2, …,}，均可通过配备具有识别和测距功能的侦察传感器执行侦察任务。因此，集群可在地面站集中指挥作用下，对部署于地面的多个任务目标进行侦察。将任务目标集合记为={,, …,}，其中，为任务目标数量，∈。

考虑到不同任务目标的执行需求存在一定差异，且多分散部署于任务空间中。因此，可划分若干任务区域，对其进行分块管理。

定义任务区域集合为={,, …,},∈，其中，≤为任务区域数量，且有={|,=1, 2, …,},∈{1, 2, …,}。

为提升任务执行效率，集群中的无人机Agent在任务执行过程中根据不同任务区域集结成(∈)支飞行编队{,, …,}，满足：∀∈{1, 2, …,},⊆,≠∅，即每支飞行编队均由有限数量的无人机Agent组成，并且规定同一无人机不能同时出现在两支不同编队中。

结合上述定义，给出无人机集群执行联合侦察任务过程示意图，如图1所示。

图1 无人机集群执行联合侦察任务过程示意图Fig.1 Diagram of UAV swarm joint reconnaissance mission

1.2 编队性能与任务需求

对于中任意一架无人机，若以地面为水平参考平面，其在任务空间中的位置坐标用(,,)表示。此外，用表示的侦察效率，其含义是无人机的单位任务执行量，即执行一次任务能够完成的工作量。对此，本文通过引入侦察半径(自身属性)对进行量化计算：记无人机的侦察半径为，则的侦察效率可等效为一个以为圆心、为半径的圆形，并通过圆形面积公式计算得到。

考虑任务载荷的计算资源、存储容量限制，每架无人机可执行的任务数量有限。因此，可通过任务资源存量表征的最大执行任务次数。基于此，可得到的侦察能力:

=·

(1)

对于集群中任意编队，假设其内部包含的无人机数量为，其联合侦察能力为

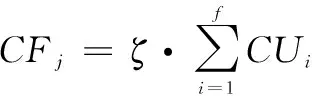
(2)

式中：为损耗因子，∈(0, 1]。

(3)

式中：为任务区域中的任务目标总数。

1.3 弹性均衡度量

在任务执行过程中，集群内各编队能力以及各区域任务需求均存在一定差异，为了确保集群能够应对持续性破坏，应充分考虑其分布式特征，避免因某一编队承担过多任务或遭受多次攻击导致编队剩余能力不足的情况，从而降低集群整体任务执行效率。因此，要求集群中各无人机编队均具备一定“弹性”，即适应并从破坏中恢复的能力。对此，本文提出一种新的度量——弹性均衡(Resilience Balance, RB)，并以此表征无人机集群在分布式任务执行过程中的均衡特性。

首先，计算无人机编队的剩余能力。对于由架无人机组成的编队, 其剩余能力计算公式为

(4)

随后，假设集群中编队数量为，由此，可基于编队的剩余能力计算无人机集群弹性均衡：

(5)

2 基于多智能体的无人机集群联合侦察任务模型

2.1 建模框架

ABM方法将无人机集群中的个体视为有决策与行为能力的Agent，通过对其属性、行为以及交互规则描述，构建自底向上的集群行为。

本文设计一种基于多智能体的建模框架，模型中各异质要素及运行过程被抽象为建模、任务、装备、环境、算法与评价等6类Agent，通过各类Agent的运行和交互描述各要素的时空动态行为。其中，建模类Agent通过顶层设计，对模型整体行为机制进行构建； 任务、装备类Agent是模型的主体部分，是对包含任务目标以及无人机、地面站和通讯的抽象； 环境类Agent对应外部环境条件及变化，一般为破坏输入； 算法类Agent则可根据环境变化，通过设计不同规则实现重构； 评估类Agent则主要结合模型输出对不同指标进行评估。

基于多智能体的建模框架如图2所示。

图2 基于多智能体的无人机集群联合侦察任务建模框架Fig.2 Multi agent-based modeling framework of UAV swarm joint reconnaissance mission

2.2 破坏行为建模方法

针对破坏行为，本文主要考虑因蓄意攻击导致的无人机整机损毁，并建立一种包含全局仿真时钟和整机故障时钟的双时钟设置机制，如图3所示。其中，全局仿真时钟以仿真模型运行为基础，随仿真推进记录集群任务执行实际时间； 整机故障时钟以集群中各无人机实际状态为基础，通过时钟跃迁清除方式模拟无人机由“可用状态”(正常)到“不可用状态”(损毁)的变化过程。

图3 面向破坏建模的双时钟设置机制示意图Fig.3 Schematic diagram of a dual-clock mechanism for damage modeling

在全局仿真时钟内，将仿真开始时刻记为，结束时刻记为，由此可得到第次仿真的总时长为

Δ=-

(6)

在整机故障时钟内，设集群中任意一架无人机的时钟存量为； 当状态为可用(正常)时，=1，当状态为不可用(损毁)时，=0。由此可知，设仿真开始时刻集群中各无人机均正常，即=1, ∀=1, 2, …,，当蓄意攻击发生在时刻并导致无人机损毁时，故障时钟直接跃迁至0，即

()=0, ∀∈{1, 2, …,}

(7)

随后，通过发生频率、发生位置以及影响范围对蓄意攻击行为进行模拟。考虑攻击发生为离散事件，可采用非齐次泊松过程表示，因此，若环境中存在次攻击事件，则其发生概率为

(8)

式中：()为一个实值常数，表示时间区间(0,]内攻击事件的平均发生次数。

对于攻击事件的发生位置，可将其抽象为任务区域中的一个质点，以的空间位置坐标(,,)为中心、为半径的球形表示攻击的影响范围。此时，记无人机的空间位置为(,,)，若满足：

(9)

则无人机损毁并退出任务，否则，不受攻击事件影响。

2.3 基于规则的重构行为建模

为避免任务中断，攻击事件发生后，集群将通过重构实现能力恢复。本文提出两种基于规则的重构方法：(1)内部协调，即确保集群中无人机数量不变，从剩余能力充足的编队抽调完好的无人机前往指定编队； (2)外部补充，即扩大当前集群规模，从前沿机场抽调完好的无人机补充至指定编队。

两种重构行为均建立在地面站Agent对其他装备Agent集中控制作用的基础上。

对于内部协调，其主要步骤包括：

Step1: 计算各编队剩余能力，将其值按照由大到小顺序排列，得到1≥2≥…≥；

Step3: 判断是否满足任务终止条件，若满足，停止重构； 若不满足，重复上一步骤。

对于外部补充重构方法，其主要步骤包括：

Step1: 计算各编队剩余能力，将其值按照由大到小顺序排列，得到1≥2≥…≥；

Step3: 判断是否满足重构结束条件，若满足，停止重构； 若不满足，重复上一步骤。

结合本文所构建的建模框架以及各类Agent功能，可将无人机集群任务执行以及破坏、重构行为分解为相对独立的Agent协同过程。其中，任务类Agent激活任务指令开始执行任务，该指令由地面站Agent传至无人机Agent并指导无人机组成特定编队，同时，无人机Agent可向地面站Agent反馈当前状态信息。此外，环境Agent负责生成破坏信息并将其发送至无人机Agent，无人机接收信息后向地面站Agent发送重构请求，并在收到重构指令后执行重构。

将以上协同过程通过图4所示的Agent行动图表示。

图4 Agent行动图Fig.4 Action diagram of Agent

3 基于仿真的弹性均衡评估方法

3.1 仿真评估流程

考虑在联合侦察任务中涉及多个无人机和任务目标，因此抽象对象是针对单次仿真试验。仿真评估过程包括: (1)建立无人机集群联合侦察任务仿真模型； (2)设置参数，初始化仿真模型； (3)统计单次仿真实验各编队剩余能力； (4)计算弹性均衡值。

图5为无人机集群弹性均衡仿真评估的流程图。

图5 无人机集群弹性均衡仿真评估流程Fig.5 Flow chart of resilience equilibrium simulation evaluation

3.2 评估算法

本文所提出的弹性均衡评估以集群中各编队剩余能力为主要依据，并根据各编队实际状态决定。其计算方法包含集群状态判定、剩余能力统计和弹性均衡计算三部分。

3.2.1 集群状态判定

根据任务执行判据，无人机集群状态可被判定为能执行任务(值为1)和无法执行任务(值为0)。具体判定规则如下：

(10)

式中：为集群的总侦察能力，即集群中所有无人机侦察能力之和；为任务空间内的任务工作总量。

3.2.2 剩余能力统计

在单次仿真中，以每支飞行编队为单位，根据式(4)对各编队在仿真时钟推进过程中各时刻的剩余能力进行统计，得到：

(11)

3.2.3 弹性均衡计算

依据式(5)和式(11)计算仿真过程中时刻的弹性均衡()：

(12)

4 案例验证

以案例验证本文所提出方法的有效性。仿真硬件为ThinkPad X1 Carbon笔记本电脑，处理器为Intel(R) Core(TM) i5-6200U CPU @2.30 GHz/2.40 GHz，内存为8 GB，基于NetLogo仿真环境实现模型运行。

4.1 仿真环境及参数设置

假设任务空间为500 km×500 km的平面地图，包含1个前沿机场和4个任务区域，每个任务区域内部随机分布不同数量的任务目标，任务目标总数为30。无人机集群规模为50架，按照任务区域组成4个飞行编队和1个备用机组(停靠在前沿机场内等待出动)，每架无人机的任务资源存量均为2。具体信息如表1～2所示。

表1 任务属性信息

4.2 仿真界面设计

为实现无人机集群弹性均衡仿真评估，建立了能够体现无人机集群联合侦察任务执行过程与破坏恢复过程的可视化仿真模型。针对模型中各类Agent行为和交互，设计了包括参数配置界面和任务执行界面的可视化场景，分别如图6～7所示。

图6 参数配置界面Fig.6 Parameter setting interface

参数配置界面中主要包括仿真实验运行、参数输入、输出等功能模块。

表2 无人机及编队属性信息

在任务执行界面中，彩色的多边形代表无人机，白色圆形代表任务目标，同一编队中的无人机通过直线相互连接表示。

图7 任务执行界面Fig.7 Task execution interface

4.3 结果分析

4.3.1 单次仿真弹性均衡评估

将策略模块参数置为1，运行仿真模型，此时，集群将在持续破坏过程中执行任务，无重构，由此得到各编队剩余能力随仿真时间变化情况，如图8所示。

图8 编队剩余能力随仿真时间变化过程Fig.8 The change curves of surplus capacity of each UAV formation with time

通过统计可知，破坏分别发生在2，5，8，11，14和17时刻，假设破坏发生后，弹性均衡变化的时间均为1个仿真步长。因此，进一步计算弹性均衡，得到如图9所示的弹性均衡变化曲线。

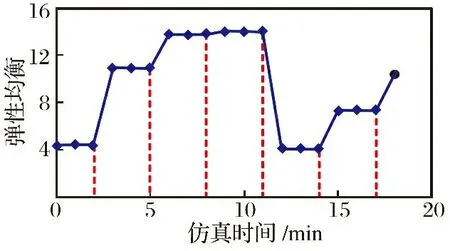
图9 弹性均衡随仿真时间变化Fig.9 The change curve of resilience equilibrium with time

显然，随着破坏的发生，集群弹性均衡值不断增加，这与编队剩余能力变化特征是一致的，即各编队剩余能力差异不断扩大； 当仿真进行到11 min时，编队剩余能力差异开始缩小，弹性均衡值出现下降； 随着破坏继续发生，剩余能力差异在14 min时开始扩大，弹性均衡也出现回升。当破坏发生在17 min时，编队无法执行任务，仿真结束。

4.3.2 内部协调重构下的仿真结果分析

考虑任务执行过程中面临的持续性破坏，集群中各编队遭受破坏的程度不尽相同，导致各编队剩余能力存在较大差异，影响任务执行。为使各编队剩余能力得到充分利用，确保集群整体任务执行，可通过一种内部协调的方法实现重构。

运行仿真模型，得到使用内部协调重构方法后，编队剩余能力随仿真时间的变化情况，如图10所示。

图10 使用内部协调重构方法时编队剩余能力随仿真时间变化Fig.10 The change curves of surplus capacity of each UAV formation with time after using the internal coordination reconfiguration method

通过进一步计算，可得到弹性均衡随仿真时间变化情况，如图11所示。已知蓄意攻击事件发生在4，7，8，10，12，14，21和31时刻，基于内部协调的重构指令依次在14，21和31发送。由图可知，随着破坏的持续，弹性均衡值不断上升； 当无人机Agent接收重构指令并进行重构后，弹性均衡值出现明显下降，且每次重构过程都使该值向更低水平变化。当仿真进行到38 min时，各编队无法通过内部协调实现重构，达到任务终止条件。

图11 使用内部协调重构方法时弹性均衡值随仿真时间变化Fig.11 The change curve of resilience equilibrium with time after using the internal coordination reconfiguration method

4.3.3 外部补充重构下的仿真结果分析

由于集群规模一定，随着破坏的持续，各编队剩余能力将出现不足。此时，需扩大集群规模，额外补充无人机Agent前往指定编队。

运行仿真模型，得到使用外部补充重构方法后，编队剩余能力随仿真时间的变化情况，如图12所示。

图12 使用外部补充重构方法时编队剩余能力随仿真时间变化Fig.12 The change curves of surplus capacity of each UAV formation with time after using the external supplementary reconfiguration method

进一步计算可得到弹性均衡随仿真时间变化情况，如图13所示。已知蓄意攻击事件发生在2, 4, 7, 11, 15, 18, 21和34时刻，重构在21和34时刻进行。由图可知，随着破坏的持续，弹性均衡仍呈上升趋势； 当重构开始后，弹性均衡值出现明显下降。第二次重构后，弹性均衡值有所回升，说明在此之前各编队剩余能力较为平均。本文将此时集群状态作为重构的终止条件。

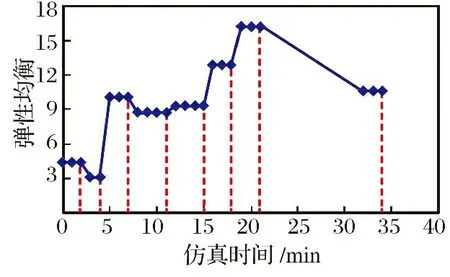
图13 使用外部补充重构方法时弹性均衡值随仿真时间变化Fig.13 The change carve of resilience equilibrium with time after using the external supplementary reconfiguration method

5 结 束 语

(1) 本文所提出的无人机集群弹性均衡度量方法，解决了无人机集群遭受破坏后剩余能力均衡的问题，为集群持续破坏下的能力设计提供支撑。

(2) 基于多智能体的建模方法，从建模框架、破坏行为以及重构行为三个方面模拟无人机集群执行联合侦察任务，为弹性均衡的仿真计算奠定基础。

(3) 所设计的可视化仿真模型从单次仿真以及包含破坏、重构行为的场景中对弹性均衡进行评估，进一步验证了该方法的有效性。