基于粒子滤波的三维转弯目标跟踪方法

冯亚强，宋 龙，张公平，2

(1. 中国空空导弹研究院，河南 洛阳 471009； 2. 航空制导武器航空科技重点实验室, 河南 洛阳 471009)

0 引 言

随着空中目标机动和突防能力的显著提升，出现了一系列复杂的机动形式，如蛇形机动、水平转弯等。为实现对机动目标的有效拦截，需要得到目标的准确运动信息，而导引头上的探测器往往只能提供有限的测量信息，且伴随着大量噪声，因此，机动目标跟踪的关键在于如何从观测信息中有效地估计出目标的状态信息。

机动目标模型的建立是机动目标跟踪的基础，一个好的模型可以有效提升目标跟踪的精度。目前有许多关于目标模型的研究成果，包括CV模型、CA模型、Singer模型、CS模型、jerk模型等。除了建立与机动目标运动情况尽可能吻合的模型外，选择与目标模型匹配的跟踪算法也是目标跟踪的关键。然而，目前提出的经典模型都是基于线性系统的模型，实际工程中往往会遇到一些非线性的机动目标跟踪问题，如果用现有的线性模型和跟踪算法进行估计，由于模型不匹配会导致滤波精度很差甚至发散。因此，针对目标做复杂机动时的非线性系统估计问题，建立准确的模型并选择与之匹配的滤波算法是机动目标跟踪的关键。

基于此，本文针对做HGB机动的目标提出了一种三维转弯模型，并建立了导弹在拦截过程中可信的动力学模型。然后，采用PF，EKF，UKF对基于三维转弯模型的系统进行估计，仿真表明，PF的估计性能优于EKF和UKF，可较好地实现对该模型的匹配。最后，基于所设计的仿真场景，采用基于粒子滤波的三维转弯模型对机动目标进行了成功的跟踪与拦截。

1 弹目运动模型的建立

1.1 目标三维转弯模型的建立

文献[5-7]提出了HGB机动形式，为战斗机提供了一种规避导弹追踪的合理方法，其机动模型可描述为

(1)

把上述模型写成状态方程的形式:

(2)

对做HGB机动的目标进行跟踪，首先要建立适合的机动目标跟踪模型，本文选取弹目相对距离及其速率和转弯角速率作为状态量，根据弹目之间的运动关系，可得到以下非线性模型：

(3)

式中：,,分别为,,方向上的弹目相对距离；为转弯速率；,分别为导弹在,方向上的位置；m,m,m分别为导弹在,,方向上的加速度；为系统噪声。

观测方程为

(4)

式中：和为视线倾角和视线偏角；和为观测噪声。

1.2 导弹动力学模型的建立

式(3)将导弹的运动信息作为确定性变量引入了状态方程中，因此，需要对导弹建立合理的、可信的运动模型。

导弹采用比例导引法拦截目标，分别计算俯仰和偏航两个方向上的过载指令：

(5)

(6)

设定导弹发动机在时刻熄火(取=5 s)，则导弹的推力可表示为

(7)

导弹飞行时的空气阻力为

(8)

综上，可建立发射后导弹的运动学模型如下：

(9)

式中：,,分别为导弹在,,方向上的位移；为导弹的速度；为弹道倾角；为方位角。

2 滤波算法的选择

2.1 不同非线性滤波方法的原理

对于式(3)～(4)所示的三维转弯模型所呈现出的强非线性特性，需要选择与之匹配的非线性滤波算法对目标状态进行有效估计。对于非线性滤波问题，比较通用的方法是利用线性化技术将非线性滤波问题转化为一个近似的线性滤波问题，再根据卡尔曼滤波理论求解，得到问题的次优解。这种利用线性化的思想得到的滤波方法即为扩展卡尔曼滤波。

无迹卡尔曼滤波同样采用了卡尔曼滤波框架，对于一步预测方程，使用UT变换来处理均值和协方差的非线性传递问题。UKF是用一系列确定样本来逼近状态的后验估计，不需要求解雅克比矩阵，对于非线性分布的统计量有较高的计算精度。

(10)

(11)

2.2 不同滤波方法的仿真对比分析

为了对比各滤波算法的跟踪性能，分别采用PF, EKF, UKF对三维转弯模型的状态进行估计。考虑到式(3)所示的模型状态量较多，因此在滤波算法仿真对比时将模型进行如下简化：

(12)

式中：为目标的位置；为转弯角速率(设定其真值为=8330+02)；为系统噪声。

仿真中，三种滤波算法采用同样的初值、系统噪声和观测噪声。为比较其估计性能，文中采用统计学中的均方根误差来衡量滤波偏差，其中，位置估计均方根误差和转弯角速率估计均方根误差分别为

(13)

(14)

(15)

(16)

三种滤波算法对目标位置及转弯角速率估计的均方根误差和CRLB下界的对比图，如图1～2所示。

图1 位置估计的均方根误差Fig.1 Root mean square error of position estimation

图2 角速率估计的均方根误差Fig.2 Root mean square error of angular velocity estimation

从图中可以看出，PF对目标位置和角速率估计的均方根误差明显低于EKF和UKF估计的均方根误差，并且PF的均方根误差更接近于各状态的CRLB下界，因此，PF对非线性模型的各状态量有更好的估计效果。

为了较全面地比较三种滤波算法的性能特点，利用各滤波算法连续仿真100次，各滤波算法的单次程序运行时间对比，如图3所示。从图中可以看出，PF的计算量最大，UKF次之，EKF的计算量最小。

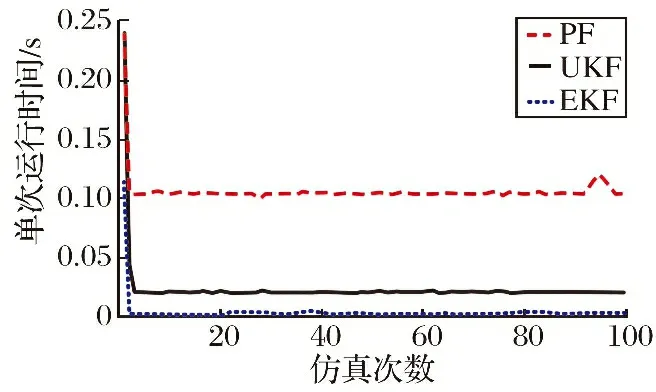
图3 各滤波算法计算量对比Fig.3 Comparison of calculation amount of each filtering algorithm

相较于EKF和UKF，虽然PF有较大的计算量，但PF对非线性模型的各状态量有更高的估计精度，因此，为了对机动目标进行准确、可靠的跟踪，本文选择用PF作为三维转弯模型的匹配滤波算法。

3 仿真验证与分析

3.1 三维转弯模型的仿真对比分析

为了验证三维转弯模型的跟踪性能，分别采用CA模型、三维转弯模型对做HGB机动的目标进行跟踪。仿真中，目标做转弯角速率固定的HGB机动，并采用同样的初值和噪声。文中采用均方根误差来衡量跟踪误差，两种目标模型对目标速度估计的均方根误差对比图，如 图4所示。

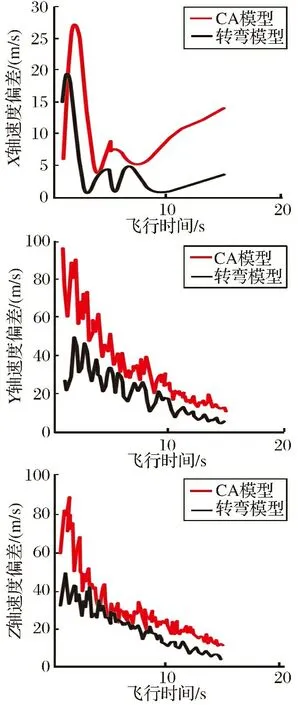
图4 不同模型的速度估计误差对比Fig.4 Comparison of velocity estimation error of each model

从图中可以看出，在对目标进行跟踪的过程中，三维转弯模型的跟踪误差低于CA模型的跟踪误差，因此，三维转弯模型有更高的跟踪精度，可以对HGB机动目标进行更有效的跟踪。

3.2 三维转弯目标跟踪仿真验证

为了验证基于粒子滤波的三维转弯模型对做HGB机动目标跟踪的有效性，设计了导弹拦截HGB机动目标的具体仿真场景，仿真参数如表1所示。

表1 仿真参数设置

仿真中采用易于实现的先验分布作为粒子滤波的重要性分布函数：

(17)

此时，各粒子对应的重要性权重可简化为

(18)

此外，除了选择合理的重要性分布函数，文中还采用了重采样技术，这在一定程度上避免了粒子滤波中的粒子退化问题，保持了粒子的多样性，从而使粒子滤波对目标的状态能够进行有效估计。

采用式(5)～(6)所示的比例导引律进行仿真，可得，导弹成功拦截目标的仿真时间为16.3 s，脱靶量为2.36 m，具有较高的拦截精度。仿真结果验证了基于粒子滤波的三维转弯模型对机动目标跟踪的有效性。

HGB机动的各状态量估计，如图5所示。从图5中

图5 HGB机动的各状态量估计Fig.5 HGB maneuver state estimation

可以看出，粒子滤波能对各个状态量进行较为理想的估计。在制导末端，有些状态量估计精度变差，这是因为由比例导引法得到的过载指令在弹道末端会有明显的抖动，而系统状态方程是以导弹的运动信息作为确定性变量，因此对估计精度具有一定的影响。

当目标在空间中以复杂的形式进行机动时，导弹依然能成功拦截目标，拦截过程中导弹和目标各运动状态的对比图，如图6～7所示。在制导末端，指令过载会急剧增大，很容易会超过导弹的过载限幅，这反映了末制导阶段的特点，对制导算法的优化具有一定的参考意义。

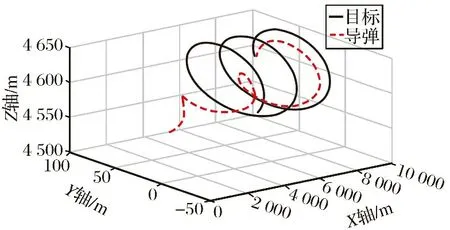
图6 弹目三维交战轨迹Fig.6 Missile-target 3D engagement trajectory

图7 弹目各运动状态对比Fig.7 Comparison of missile-target motion states

4 结 论

针对目标发生转弯的运动模式，提出了三维转弯模型，然后对三维转弯模型的跟踪性能进行了对比验证，并基于此模型对不同滤波算法的性能进行了仿真对比，最后选择用粒子滤波对基于三维转弯模型的机动目标进行跟踪。从仿真结果可以得出以下结论：

(1) 本文提出了三维转弯模型，仿真结果表明，对于一些机动形式复杂的目标，相较于CA模型，三维转弯模型有更高的跟踪精度。

(2) 文中设计了一种基于粒子滤波的三维转弯模型，仿真结果表明，粒子滤波对三维转弯模型的各状态量具有更高的估计精度，这种机动目标跟踪方法对做HGB机动的目标具有良好的跟踪效果。

(3) 建立了导弹在拦截过程中较为合理、可信的动力学模型，得到了相对真实的导弹运动过程。