CDI二维浓度传质模型的建立以及实验验证
黄陆月,刘畅,许勇毅,邢浩若,王峰,马双忱
(1华北电力大学环境科学与工程系,河北 保定 071003;2中电华创电力技术研究有限公司,江苏 苏州 215123)
引 言
电容去离子技术(CDI)是一种将盐水淡化的水处理技术。因其能耗低、操作方便、维护简单、去除效果好等优点,引起了学者们的广泛关注[1-3]。CDI的基本原理是通过电场力的作用,在电极表面形成双电层,利用带电电极表面的电化学特性来实现对水中的带电离子的捕集[4]。影响CDI 脱盐性能的关键因素有很多,例如:结构[5-6]、电极材料[7]、流速、电压、浓度以及运行方式[8]等。因此,厘清CDI 除盐机制以及建立传质预测模型对CDI今后的设计与发展显得重要。
CDI 传质过程以及存储特性的理论概念,已经被广泛研究[9]。Helmholtz-Perrin 模型(简称H-P 模型)是最早的固液相界面双电层电荷分布模型[10]。该模型认为在固液界面中可能存在电荷分离,即假设所有表面电荷都是通过吸附在表面的反电荷直接补偿的。这两种电荷之和为零,也就是说,作为一个整体,EDL 是不带电的。但是,Helmholtz-Perrin 模型不能充分描述多孔CDI 电极中的EDL结构,这是因为离子不会在紧挨着表面的平面上凝聚,而是在接近表面的一层上扩散分布。到了20 世纪,分散层Gouy-Chapman 模型被提出[11],该模型离子并没有像H-P 模型所考虑的那样在凝聚层中表面吸附,而是由于它们的热运动而留在溶液中。Gouy-Chapman 模型对扩散层的关键假设是,为了补偿表面电荷,存在两种路径:第一种是相反的离子在扩散层被吸附,而第二种是共价离子脱附,这意味着在无电荷的情况下靠近表面的离子会被释放出来[12]。而在之后的研究中,Gouy-Chapman-Stern 模 型(简 称G-C-S 模 型)被 提 出[13-14]。该模型认为在扩散层与电极内层之间还存在着Stern 层。Stern 层内的电荷分布遵循H-P 模型的规律分布,在Stern 层外面的电荷遵循Gouy-Chapman模型的规律特点。该模型假定在孔壁上形成的扩散层可以自由延伸。但实际上,在吸附材料的孔隙中很难实现脱盐[15]。为了模拟离子在EDL中的吸收,需探究离子在CDI中的传质过程。Biesheuvel等[16]对多孔电极模型开展研究,分析了多孔碳材料中的离子吸附情况及其相关性质,得出了电极的离子容量取决于双电层容量、施加的外电压以及可用的表面积的结论。该模型假设处于一维空间下,可以预测超级电容器充电时的动力学过程。但这个模型可能不适用于描述具有纳米尺度孔隙的多孔介质中的充电。基于此,修正的Donnan 模型很好地解决了这个问题,该模型认为盐储存在微孔(孔径<2 nm)体积内,而不是在微孔表面。修正的Donnan 模型[17]不仅对CDI 传质过程有着更加确切的模拟,而且克服了在高浓度条件下,使用Gouy-Chapman-Stern 模型进行数值模拟脱盐和盐浓度梯度 变 化 的 困 难[18]。2011 年,Biesheuvel 等[19]提 出 了修正的道南模型(mD 模型)。该模型考虑了盐分的存储发生在小于2 nm 的微孔体积内,而不是在孔表面(如Helmholtz 或GCS 双电层结构模型建立的模型所假定的)。综上,双电层模型有向更加复杂、微观且细致方向发展的趋势。以下介绍几种具有代表性的传质模型。
(1)Biesheuvel等的动态吸附解吸模型 Biesheuvel等[20]根据Newman 等[21]在多孔电极上的模型研究和经典的G-C-S 双电层模型[22],设计了一种针对CDI的吸附解吸模型。该模型通过假设在电极前面存在一个限制离子传输的传质层(扩散层或薄膜层)来描述从本体溶液到界面的电荷传输。在这种方法中,忽略了离子浓度梯度作为运输的动力(扩散传输),只考虑电场的影响。传质层的电荷传输速率由溶液离子浓度、传质系数和静电驱动力的乘积而得:
Jcharge=kcΔφmtl(1)
式中,k为传质系数;c为溶液离子浓度;Δφmtl为静电驱动力。
从模型的效果来看,理论模型的预测与吸附实验的结果一致性很高,但与解吸实验结果不太吻合,需要通过减小流动室的体积来对模型进行改良。而离子解吸步骤与吸附步骤的内部体积不会相差较多,需要更详细的模型来计算CDI 中液体的流动状况以及溶液进出电极的离子传输过程。
(2)Suss等的模型 在大多数CDI系统中,溶液流动的方向通常与电场方向垂直(FB-CDI)。而Suss 等[10]发现与FTE-CDI(进料流向直接穿过电极本身并平行于施加的电场方向的CDI)相比,传统的FB-CDI 脱盐所需的时间较长[23]。在液体流动方向与电场方向一致的情况下,Suss 等以宏观多孔电极(MPE)理论为基础,假定CDI 中溶液是静止的,建立如下模型:

式中,jads-i为离子i的净摩尔通量,mol/(cm2·s);cbulk-i为离子i的浓度,mol/cm3;w为装置宽度,cm;Q为 溶 液 流 速,cm3/s;H为 极 板 间 距,cm;t为 时间,s。
等式右边第一项表示离子在电中性体溶液中的传输(x方向上),表明该模型考虑了沿CDI 液体流动的变化。在该模型中,对传质最重要的区域称为对流-扩散层,对流-扩散层有完全态和进行中两种状态。在完全态的对流-扩散层中[18],溶液中离子在传输的过程中均匀分布,当主体溶液边缘的离子被电吸附到电极上时,电极之间的离子会迅速重新排列,降低沿流动方向的浓度梯度,其净平均摩尔通量可以表示为:
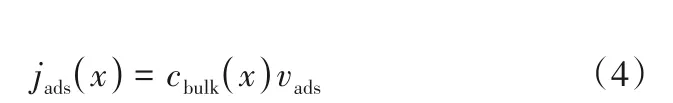
式中,jads为离子从本体溶液中被吸附的净摩尔通量,mol/(cm2·s);vads为净吸附速度,cm/s。
而在进行中的对流-扩散层中的流速很大,主体溶液中的离子未能向双电层迁移,只有电极附近的一小部分的离子会被吸附,传质效应仅发生在电极-溶液界面附近处,可以按Nernst 层进行处理得到:
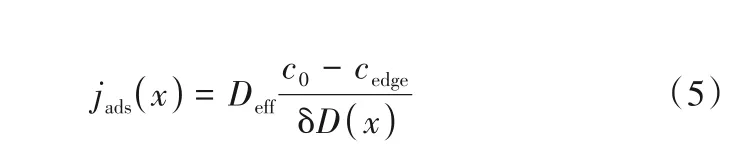
式中,jads为离子从本体溶液中被吸附的净摩尔通量,mol/(cm2·s);Deff为有效扩散系数,m2/s;cedge为界面处的浓度,mol/m3;c0为入口溶液的浓度,mol/m3;δD为Nernst层厚度,m。
Perez 等的模型很好地预测了低流速和高流速下溶液的脱盐效果。在低速时,完全态的对流-扩散模型预测更准确,高速时进行中的对流-扩散模型预测更准确。该模型可以评估现有CDI系统性能以及设计和扩展新模型。不足之处在于该模型只适用于低浓度的溶液,且按Nernst 层进行处理会存在一定的误差。

通过最小化实验和模型预测结果之间的误差来确定参数值,独立参数pm则通过动态测量出口水中盐浓度的时间分布确定。最后得到的模型参数与实际值有较好的一致性[28]。由于该模型是模块化,故可以很容易地用更精确的EDL 模型进行修改,为后续的研究提供了便利[29]。该模型不足之处在于:首先,在模型中假设恒定的微孔电容不够精确(可以通过将微孔电容与微孔电荷状态相关来改良模型);其次,CDI 中常用的模型标定方法主要是在平衡时测量,忽略了系统是动态变化的。表1 为这几种模型的优缺点对比。

表1 传质模型优缺点对比Table 1 Comparison of pros and cons of CDI mass transfer model
综上可以看出,目前CDI 传质模型大多数为一维模型,具有简单和易于实现的优点。然而,CDI系统内部之间的实际流动通常涉及两个重要的方向:一个是电极间水流的方向,另一个是外加电场的方向(垂直于流动方向)。因此,二维模型的模拟结果更贴近实际情况。此外,探究CDI 在除盐过程中的扩散过程以及内部浓度分布情况,对于理解CDI 除盐的微观机制具有重要帮助。为此,本文提出了一种新型CDI 浓度传质模型,该模型考虑了沿流向方向和垂直流向方向上的浓度变化情况,通过实际实验参数进行了实验验证,并对模型参数予以修正。之后,为了更加直观地观测浓度分布情况,利用COMSOL 软件对该二维模型进行模拟。根据模拟结果,综合分析了CDI 在传质过程中的主要影响因素,并对装置结构提出合理化建议。
1 模型的建立与验证
1.1 模型的推导与建立
根据前述,运输的离子在CDI 装置中的传质有电迁移、扩散和对流三种形式,为了计算方便,现忽略对流的影响。
1.1.1 电迁移传质过程 在主体溶液中,电迁移的传质公式为[30]:


式中,R为摩尔液体常量,Pa;T为温度,K。

由此建立了流向上和垂直流向上的预测模型,该模型可以预测出随着CDI 除盐的进行,时间与液体浓度的变化关系,并可以利用CDI 除盐实验结果对其预测效果加以验证。
1.2 模型的验证
根据实验可设定初始参数,见表2。

表2 参数设置Table 2 The parameters setting in 2D mass transfer model
(1)在流向方向上,取t=1 s,将参数输入MATLAB 2014b,利用该软件进行模拟,得到在氯化钠浓度为100 mg/L 时,其浓度随距离变化的曲线见图1。

图1 浓度随距离的变化Fig.1 The predicted curve of concentration vs distance by model
x=0.09 m 的出口处,浓度随时间的变化见图2。图2 的曲线与实际不符,浓度应随时间的增长呈下降趋势,这是由于建立的式(20)中,距离x的系数为正,因此与浓度c呈正比关系。故该模型不能反映浓度随时间的变化。尝试建立新的沿流向的模型:
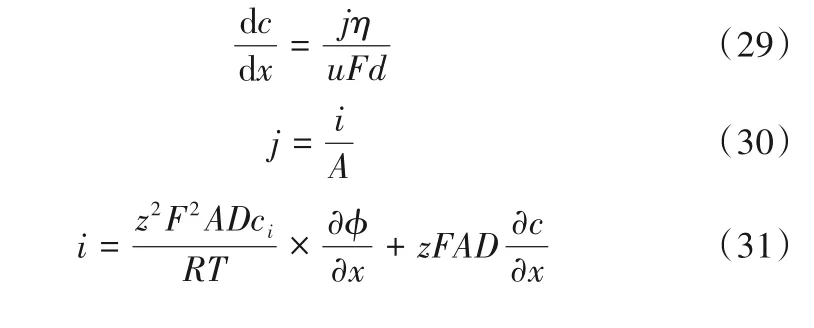

图2 浓度随时间的变化Fig.2 The predicted curve of concentration vs time by model
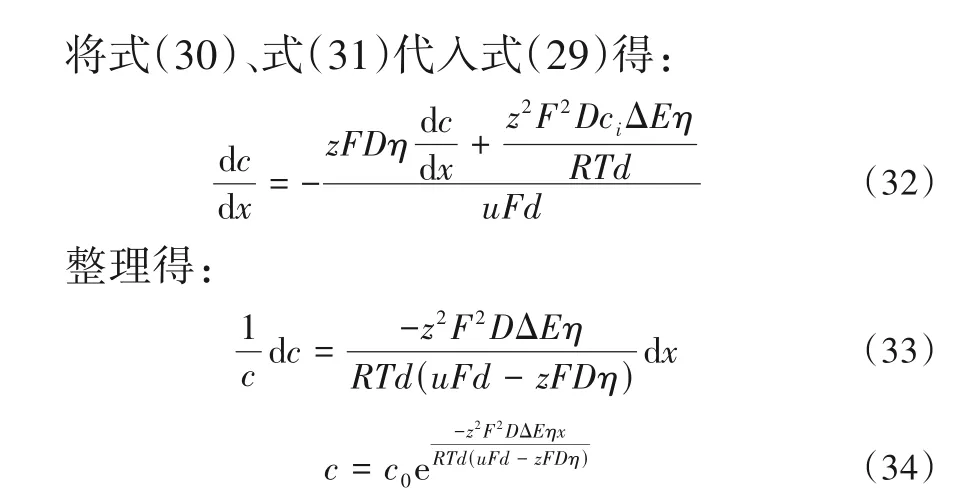
拟合得到图3。从图3的曲线可以看出,浓度随着距离的增大而降低,相较于原模型,该模型中浓度下降的趋势更加合理。但该模型中没有时间变量,因而无法得到浓度随时间变化的关系,故尝试用垂直流向的数学模型对实验数据进行处理。
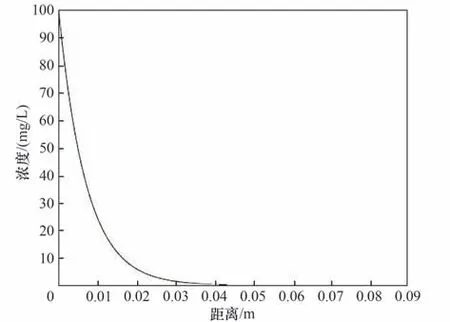
图3 修正模型浓度随距离的变化关系Fig.3 The predicted curve of concentration vs distance by modified model
(2)在垂直流向的方向上,将y=0.00001 m 处的浓度作为出水浓度,先用MATLAB 2014b 软件进行拟合,得到浓度随时间变化的曲线,见图4。

图4 垂直方向浓度变化拟合曲线Fig.4 The fitting curve of concentration change in vertical direction
将实验得到的不同初始浓度下的实验数据与之进行对比,得到图5。
由图5可见,二者趋势大致相同,模型有一定的合理性,尤其是在100 mg/L 时模型与实验数据拟合度最高。此外可以看出,浓度越低该模型的拟合效果越好。这可能是由于在建立模型时未能考虑流速对于电吸附效果的影响,存在实验过程中离子未能与吸附材料充分接触的情况,因而实验测得的离子浓度高于理论计算值。

图5 模型与实验的对比Fig.5 Comparison of 2D model and dynamic experiment results
2 COMSOL仿真模拟
COMSOL软件可以用来模拟适用于诸多工程应用领域的专业模型[31]。为模拟出前文所述的浓度传质过程,利用COMSOL Multiphysicstip 5.5仿真软件,将X轴方向上的式(34)以及Y轴方向上的式(28)代入,建立了电迁移与流动耦合的二维仿真模型。根据模型的特点,在X轴、Y轴方向以及X轴与Y轴联立的三种情况下,分别模拟分析了电压、流速一定的状态下,CDI 内部空间上的传质过程以及浓度分布情况。根据实验所采用的CDI 装置结构特点,建立了如图6 所示的模型结构。模型为5 cm×5 cm 的正方形结构,左下角的圆代表入水口,右上角的圆代表出水口,蓝色的线为电场施加位置,由上向下施加。

图6 COMSOL模型结构Fig.6 COMSOL model structure
根据上述的模型结构,模拟出了在施加电压后的电场强度分布情况,如图7 所示。由于实验中的直流电源施加的电压为1.2 V,所以将模型中的额定电压设置为1.2 V。观察图中电场强度变化,可以发现在施加电压附近的电场强度最高,随着距离的增加,电场强度逐渐下降。甚至在最后的底端,电压几乎为0。由此可以看出,在单一方位施加电压会造成电场强度分布不均的情况。

图7 电场强度分布COMSOL模拟图Fig.7 Electric field intensity distribution by COMSOL simulation
CDI 模型结构在X轴和Y轴的流线分布如图8所示。可以看出,由于入口到出口的位置处于45°倾斜摆放,所以X轴和Y轴方向速度场所呈现的流线大致相同。值得注意的是,在X轴和Y轴方向的流线分布图中,左上角和右下角部分都会呈现出不同程度的死区(即涡流),这会导致流线分布不均匀的情况发生,体现出了这种CDI 结构在设计上的局限性。
CDI 的浓度分布模型是本文的重点研究对象。浓度传质模型以500 mg/L 的初始浓度为研究条件,探究了X方向、Y方向以及XY方向上的浓度分布情况。图9 为X方向上的浓度分布模拟图。观察图可以发现,浓度从左下角至右上角呈递减分布。结合图8 分析,即说明顺着水流流动的方向浓度逐渐降低。因此可以得出,随着距离的增加,浓度随之降低。这一规律也与之前MATLAB 模拟计算得出的趋势一致。
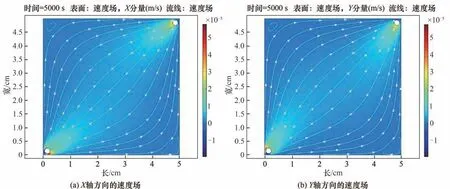
图8 流线分布COMSOL模拟图Fig.8 Streamline distribution by COMSOL simulation

图9 X方向的浓度分布COMSOL模拟图Fig.9 Concentration distribution in the X direction by COMSOL simulation
图10 为Y方向、不同时间点的浓度分布模拟图。与X方向不同,可以看到,随着时间的推移,Y方向的高浓度区域在逐渐靠近入口(即图底部),这说明起到吸附作用的位置主要集中在中下部。图11为X方向与Y方向联立(简称XY方向)的浓度分布 模 拟 图。可 以 发 现,在t=0 s 时,图10(a)与图11(a)无明显变化。而随着时间的增加,在图11中左侧部分明显浓度有所升高,这是考虑X方向上浓度分布的缘故。

图10 Y方向浓度分布的COMSOL模拟图Fig.10 Concentration distribution in the Y direction by COMSOL simulation
通过之前介绍的理论了解到,CDI 离子吸附过程主要包括离子的扩散传输过程和双电层对离子的内扩散吸附。因此,该吸附过程是一种离子扩散以及电场迁移综合作用的动力学过程。观察模拟图中浓度随时间的变化可以发现,当CDI 被施加电压开始除盐工作时,离子通过电迁移和扩散在装置内部累积,并且在其内部形成一个“下低上高”的浓度梯度。在考虑了X方向上的离子分布后可以看出,装置左侧部分的浓度略高于右侧。当时间到10 s 时,底部浓度已经达到初始浓度的5 倍。在此阶段中,离子通过电迁移和扩散传输到达吸附材料内部。此时的CDI 是在电场迁移、扩散传质以及离子吸附三种机制的共同作用下进行的。并且,随着离子吸附过程的进行,这个高浓度区域在逐渐减小。此外还可以看出,随着时间的推移,浓度聚集区域在逐渐下移。值得注意的是,CDI 通电后靠近界面的吸附材料微孔迅速带电,而远离通电界面的微孔则保持部分带电。但是浓度富集区域却向电场较小的方向移动,由此推断装置内部是以扩散传输为主的物理吸附。对比50 s和5000 s 的模拟图[图11(c)、(d)],可以看到浓度聚集区域下移并不明显。这是由于此时的传质主要是由扩散传质机制起作用,通过扩散传输的方式向CDI 提供新的离子。离子从本体溶液扩散迁移至吸附材料内部,再加上一部分离子被吸附到带电的微孔中,导致电极内微孔浓度变化明显。盐离子沿流向方向的传输和持续的局部吸附,使离子以类似于冲击波的形式运动[32]。此过程与平流和扩散之间的平衡有关,并且涉及快速和慢速两种动力学过程。综合分析得出:与离子的电迁移相比,离子的扩散传输是脱盐速率提升的主要因素。

图11 XY方向浓度分布的COMSOL模拟图Fig.11 Concentration distribution in the XY direction by COMSOL simulation
综上可以看出,COMSOL 软件可以很好地模拟出该二维CDI 浓度传质模型,从模拟出的结果不难看出,这种CDI 结构存在着一些设计上的缺陷。首先,电场分布不均。单一方向施加电场会造成离电场强度近的区域电吸附效果较好,而离电场强度远的区域电吸附效果较差,甚至会出现仅有物理吸附的情况。解决此问题的方法是可以从多方向施加电场,尽可能地使电场均匀分布在电极表面。其次,在流场分布图中可以看到,有部分角落会出现死区的情况。解决此问题的方法是在CDI 装置底部的两个底角都设置进液口,而在装置顶部的两个角均设置出液口,这样就可以有效地减少死区范围。
3 结 论
本文对现有的理论传质模型进行了详细论述,并总结出这些模型各自的优缺点。基于已有传质模型的经验,建立了一种新型的二维浓度传质模型。该二维模型考虑了流向方向和与流向垂直方向两种情况,并且兼顾了电场迁移以及传质扩散等因素。之后,利用实验数据对此二维模型加以验证和修改。此外,通过COMSOL 软件对该模型进行预测分析。根据模拟结果,详细讨论了CDI 在除盐过程中内部离子的迁移情形以及浓度分布情况,指出CDI 装置在结构上的设计缺陷,并给予合理化建议。新型二维浓度传质模型能够为CDI 装置结构的设计优化以及浓度传质研究提供理论依据。

