计及网络谐振结构的双馈风电场次同步振荡问题分析及抑制

邢法财，武 诚，蒋 哲，张 冰，杨 冬，周 宁

（1. 国网山东省电力公司电力科学研究院，山东济南 250000；2. 国网山东省电力公司电力调度控制中心，山东济南 250000）

0 引言

双馈感应风力发电机（DFIWG）（简称为“双馈风机”）［1］的重量较轻、尺寸较小、成本较低，且其能够适应较为广泛的风能状况，是目前风电场普遍采用的风机类型。但当双馈风电场通过串联补偿线路送出时，系统频繁出现一些振荡问题［2⁃3］。为此，本文致力于从电力网络谐振的角度深入探究双馈风电场的振荡机理，并提出相应的抑制措施。

双馈风电场经串补送出时发生的振荡现象，其振荡频率多在次／超同步频段，学术界一般将其归属为次同步振荡的研究范畴［4⁃6］。但鉴于风机轴系的自然扭振频率较低，故风电场的振荡不属于扭振相互作用、暂态扭矩放大等［7］传统的涉及发电机轴系的次同步振荡形式。现有文献大多从感应发电机效应或次同步控制相互作用等角度对其进行分析，多采用单机串补无穷大系统。文献［8］采用频率扫描法和时域仿真法分析发现，受串补度、风速、控制器参数等影响，感应发电机效应和次同步控制相互作用这2 种形式的次同步振荡均有可能发生在双馈风机经串补送出系统中；文献［9］基于双馈风机经串补送出系统的等效电路，指出风电场振荡的感应发电机效应是一种双馈风机控制器参与的感应发电机效应；文献［10］基于详细的双馈风机经串补送出系统的状态空间模型，分析发现风电场振荡的次同步控制相互作用是由串补和风机换流器相互作用所引起的，受串补度和控制器参数共同影响；文献［11］根据现场数据确定了风电场的振荡不涉及风机轴系，其属于电气谐振，且串补度和运行转速分别是影响稳定性和振荡频率的关键因素；文献［12］基于状态空间模型对比了单机等值模型与多机模型对双馈风机次同步振荡分析的影响。由于双馈风机含有背靠背换流器，一些专家学者从电力电子装置稳定性的角度出发对双馈风机引起的振荡问题进行分析，如文献［13⁃14］基于双馈风机阻抗模型的奈奎斯特稳定判据，分析发现电力网络和换流器控制器相互作用是引起双馈风电场经串补送出时发生振荡现象的主要原因。

由现有研究可知，双馈风电场经串补送出时的振荡问题属于电气谐振的研究范畴，所以该问题也可以从电力网络谐振的角度出发进行分析。相较于已有的研究，从电力网络谐振角度进行分析可以充分考虑电力网络的拓扑结构，能够涵盖更多的电力系统元件，对于宽频段谐振模式的分析更为全面。s域节点导纳矩阵法［15⁃16］建立在传统阻抗建模的基础上，是一种可以充分计及电力网络拓扑结构的网络谐振分析方法，本文采用该方法从电力网络谐振角度分析了运行工况对双馈风电场振荡问题的影响，并提出了基于旁路阻尼滤波器的振荡抑制措施。

首先，本文对双馈风机的基本结构进行了介绍，并对其交流侧受扰动时的响应特性进行了分析，建立其端口阻抗模型。在此基础上，基于s域节点导纳矩阵法，分析了不同串补度和运行转速下双馈风电场经串补送出系统的网络谐振结构，以确定运行工况对风电场振荡问题的影响。最后，针对最不稳定的谐振模式，提出了基于旁路阻尼滤波器（BDF）的谐振抑制措施，并通过电磁暂态仿真对其有效性进行了验证。

1 双馈风机的基本结构

目前部分文献对双馈风机进行阻抗建模［13⁃14］，但均对双馈风机的基本结构进行了不同程度的简化处理，建模所考虑的环节尚不完善。为此，本文从双馈风机的基本结构入手，采用传递函数分析其扰动响应特性，建立其端口阻抗模型，并进行仿真验证。

双馈风机的“双馈”源自于其发电机定子和转子均可向电网馈入功率，定子直接与电网相连，转子通过背靠背换流器与电网相连，其基本结构［1］见附录A 图A1。双馈风机的背靠背换流器可分为转子侧换流器（RSC）和电网侧换流器（GSC）两部分，二者均为两电平电压源型换流器。转子侧换流器一般用于控制发电机的转矩，以捕获更多的风能；而电网侧换流器一般用于控制换流器的直流侧电压和输出无功功率，以支撑换流器的稳定运行和调节无功补偿，它们的控制系统结构见附录A 图A2，控制系统中的变量参数定义见附录A表A1。

双馈风机转子侧换流器和电网侧换流器的控制系统结构与常规两电平电压源型换流器［17⁃18］相类似，均为内外环控制结构。外环为功率控制环，响应速度较慢，在分析中高频段（［5，1000］Hz）的扰动响应特性时，一般可忽略其影响；内环为电流控制环，跟踪外环输出的电流参考，以实现外环的控制要求，对双馈风机的宽频段扰动响应特性影响较大，在阻抗建模过程中需详细考虑。另外，锁相环也是影响双馈风机宽频段扰动响应特性的重要环节，需详细考虑。电网侧换流器通过锁相环与电网保持同步，即坐标变换采用锁相环的输出相位；而转子侧换流器坐标变换所采用的相位为锁相环输出相位与发电机转子相位的差值，现有文献对此少有阐述。

2 双馈风机的端口阻抗模型

基于双馈风机的基本结构，设背靠背换流器的直流侧电压恒定，采用传递函数对双馈风机的交流侧扰动响应特性进行分析，建立其端口阻抗模型。

2.1 阻抗建模

首先，本文对扰动分量在双馈风机内部的流动情况进行了定量计算，推导出扰动分量在背靠背换流器内部的传递函数，详细推导过程见附录B 式（B1）—（B27），最终推导结果见式（1）—（3）。

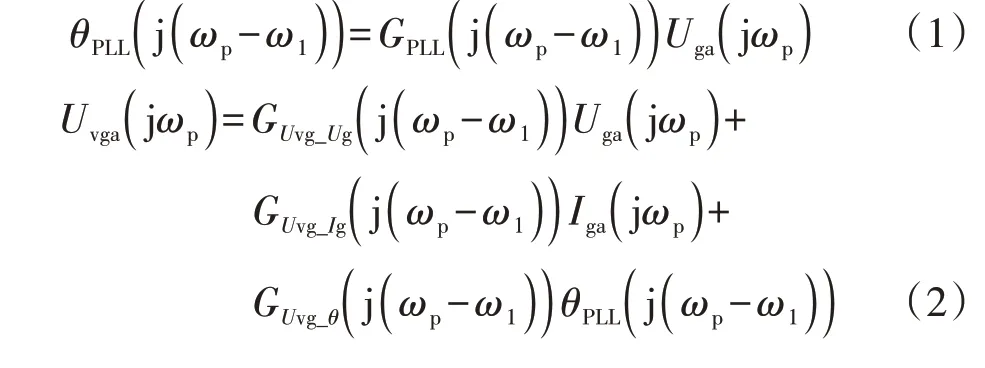
进而，本文分析了背靠背换流器的外部电路：电网侧换流器外部为平波电抗器，可用电阻和电感的串联电路进行模拟；转子侧换流器外部为异步发电机，其等效电路见附录C 图C1。结合扰动分量在背靠背换流器内部的传递函数以及背靠背换流器的外部电路，可建立双馈风机的端口阻抗模型，如式（4）、（5）所示。

2.2 模型验证

为验证所建立端口阻抗模型的准确性，本文搭建了双馈风机的电磁暂态仿真测试环境。在仿真过程中，通过测试信号法获得双馈风机的端口阻抗频率特性，即在双馈风机交流侧电压中叠加不同频率的扰动信号，测量其交流侧电流中相对应的扰动分量，以计算端口阻抗频率特性。需要说明的是，扰动信号的施加不能对系统的稳态运行点产生影响。

在［1，100］Hz 的频率范围内，双馈风机端口阻抗频率特性的仿真结果与解析结果如图1 所示。图1 表明，双馈风机电网侧换流器端口阻抗以及发电机定子侧端口阻抗的仿真结果均与解析结果相吻合，验证了端口阻抗模型的准确性。另外，由图1（b）可知，在［10，60］Hz的频率范围内发电机定子侧端口阻抗实部为负值，即存在一定的负电阻效应。由负电阻效应理论可知，若系统的谐振点恰好位于负电阻效应频段，且正电阻不足以抵消负电阻时，则系统便会存在谐振风险。因此，双馈风机的异步发电机及其转子侧换流器是引起双馈风电场振荡问题的重要原因。

图1 双馈风机端口阻抗的频率特性Fig.1 Frequency characteristics of port-impedance of DFIWG

3 双馈风电场的次同步振荡问题研究

IEEE 9节点标准测试系统是电力系统领域常用的标准测试算例，本文将其改造为双馈风电场经串补送出的测试系统，以便从电力网络谐振的角度研究双馈风机经串补送出时的振荡问题。

测试系统的拓扑结构如图2 所示，双馈风电场的并网参数如附录C 表C1 所示。s域节点导纳矩阵的建立依赖于电力网络的拓扑结构，首先将电力网络中各节点依次进行编号，建立节点导纳矩阵的维度；然后依次遍历所有节点，根据电力网络的拓扑结构，在节点导纳矩阵的对角元及非对角元填入节点的自导纳及互导纳。

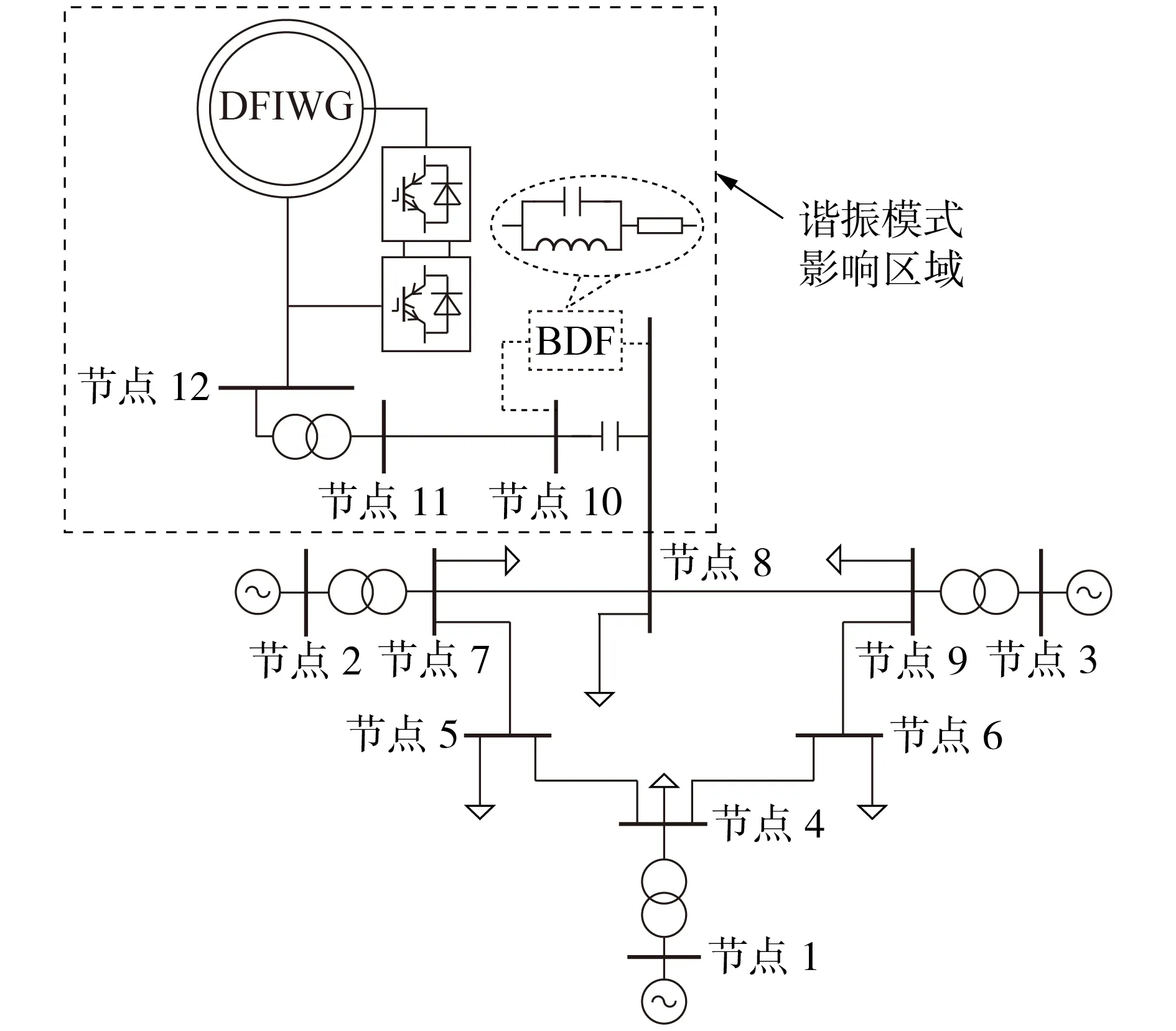
图2 双馈风电场经串补送出系统Fig.2 DFIWG-based series-compensated transmission system

需要说明的是，在双馈风机单机端口阻抗的基础上，双馈风电场的阻抗主要通过双馈风机阻抗的并联获得，即双馈风机单机阻抗除以双馈风机台数。双馈风电场阻抗作为其并网节点的自导纳填入节点导纳矩阵的对角元。s域节点导纳矩阵的形式如式（6）所示。

3.1 网络谐振结构分析

针对该测试系统，本文采用s域节点导纳矩阵法［15⁃16］对其在不同线路串补度和转子运行转速下的谐振结构进行了分析。所关注频段为次／超同步频段，分析结果如表1 所示。表中：Kc为并网线路串补度；σres为衰减因子；fres为谐振频率。

表1 测试系统的谐振结构分析结果Table 1 Analysis results of resonance structure about test system

从表1 可以看出，在不同线路串补度和转子运行转速下，测试系统在次／超同步频段内均仅存在1 种谐振模式，其谐振频率在［14，25］Hz 的频率范围内变化，而其衰减因子在线路串补度为50%、转子运行转速为0.8 p.u.以及线路串补度为70%、转子运行转速为0.8 p.u.和0.9 p.u.的运行条件下为负值，即为不稳定谐振模式，这表明测试系统在这些运行条件下会存在一定的谐振风险，需要加以抑制。

另外，通过对比可以发现：在同一线路串补度下，双馈风机的转子运行转速越小，则系统谐振模式的衰减因子越小，即谐振模式越不稳定；而在同一转子运行转速下，系统谐振模式的衰减因子也会随线路串补度的变化而发生较大变化，但变化规律不明显。总体而言，线路串补度越高，系统发生谐振的风险越大。

3.2 仿真验证

为验证上述谐振结构分析结果的准确性，本文在PSCAD／EMTDC 电磁暂态仿真软件中搭建了测试系统的仿真模型，对不同运行条件下测试系统的运行情况进行了仿真测试，测试结果如图3 所示。图中区间1—4 分别对应ωm的值为1.2、1.1、0.9、0.8 p.u.。进一步地，本文对双馈风电场输送功率中的振荡分量进行了分析，其频谱如图4 所示。图中工况1—3 分别对应Kc=50%、ωm=0.8 p.u.，Kc=70%、ωm=0.9 p.u.，Kc=70%、ωm=0.8 p.u.。

图3 双馈风电场输送功率的仿真波形Fig.3 Simulative waveforms of output power of DFIWG-based wind farm

图4 双馈风电场输送功率的频谱图Fig.4 Frequency spectrum of output power of DFIWG-based wind farm

图3和图4表明，当测试系统处于线路串补度为50%、转子运行转速为0.8 p.u.以及线路串补度为70%、转子运行转速为0.8 p.u.和0.9 p.u.的运行条件下时，系统会出现振荡失稳现象，且振荡频率与表1中的分析结果基本一致，验证了谐振结构分析结果的准确性。值得注意的是，图4 中所标注的频率38 Hz（22 Hz）表示双馈风电场输送功率中振荡分量的频率为38 Hz，其工频互补频率为22 Hz，即对应表1中谐振频率为21.4 Hz。谐振模式的谐振频率描述的是电压、电流量中振荡分量的频率，与功率量中振荡分量的频率呈工频互补关系，即两者之和为工频频率，算例中系统工频为60 Hz。

4 基于旁路阻尼滤波器的谐振抑制措施

为保证双馈风电场并网系统的安全稳定运行，上述运行条件下所存在的不稳定谐振模式必须加以抑制，本文通过对不稳定谐振模式的影响区域进行定位，提出了一种基于旁路阻尼滤波器［19⁃20］的谐振抑制措施。

4.1 不稳定谐振模式的影响区域分析

对表1 中最不稳定的谐振模式（σres≈-18.22 s-1，fres=24.0 Hz）（简称“24.0 Hz 谐振模式”），本文分析其节点电压振型向量和参与因子矩阵，分析结果如图5和表2所示，表中幅值为标幺值。

图5 24.0 Hz谐振模式下的节点电压振型向量图Fig.5 Diagram of nodal voltage oscillation type vector under 24.0 Hz resonance mode

表2 24.0 Hz谐振模式下的参与因子矩阵元素Table 2 Elements of participation factor matrix under 24.0 Hz resonance mode

图5 表明，24.0 Hz 谐振模式下的节点电压振型向量中存在2 组振型相位相反的节点群，故该谐振模式为电网断面谐振模式，表现为2 组节点群之间的谐振，即节点10—12对节点7—9的谐振。另外，从表2 也可以看出，节点8、10—12 等为该谐振模式的主要参与节点，故该谐振模式主要由双馈风电场及其并网线路、串补电容所引起，其主要影响区域为双馈风电场的并网区域，如图2中虚线框所示。

4.2 加装旁路阻尼滤波器的抑制策略

鉴于24.0 Hz 谐振模式为次同步频段的谐振模式，且其涉及双馈风电场并网线路的串补电容，所以本文采用旁路阻尼滤波器对其进行抑制。

旁路阻尼滤波器与串补电容相并联，其安装位置及其结构如图2 中虚线框所示。系统工频下，旁路阻尼滤波器的电感和电容发生并联谐振，该支路表现为断路状态，对系统的稳态运行点无影响；而在次同步频率下，旁路阻尼滤波器整体呈现阻感特性，可以为扰动电流提供一条流通路径；进而，可以通过合理设计滤波器参数耗散扰动能量，对谐振模式加以抑制。

鉴于系统工频下旁路阻尼滤波器的电容必须与电感发生并联谐振，所以其只剩下电阻和电感2 个参数可以自由设计［20］。首先对滤波器电感进行设计，其设计思路为使旁路阻尼滤波器和串补电容在谐振频率附近发生并联谐振以阻隔次同步电流流通，其计算公式如式（7）所示。然后可以通过选定值校验的方式确定滤波器电阻。

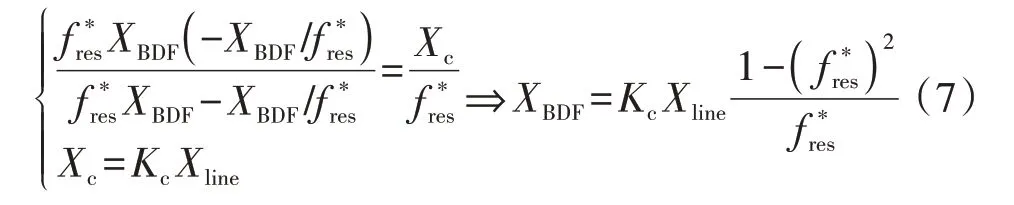
式中：XBDF为旁路阻尼滤波器的电抗；Xc为串补电容的电抗；Xline为并网线路的电抗；f*res为谐振频率的标幺值。

针对24.0 Hz 谐振模式，根据式（7）计算可得旁路阻尼滤波器电抗XBDF=0.514 5 p.u.，而旁路阻尼滤波器电阻RBDF则可以选定为0.05 p.u.、0.10 p.u.和0.20 p.u.，本文对安装旁路阻尼滤波器后系统的谐振结构重新进行了分析，以校验滤波器参数设计的有效性，分析结果如表3 所示。由表可知：当安装旁路阻尼滤波器后，测试系统在RBDF为0.10 p.u.和0.20 p.u.的情况下双馈风机运行于不同转速时基本没有谐振风险；但在RBDF为0.05 p.u.的情况下双馈风机运行于1.1 p.u.和1.2 p.u.的转子转速时会存在谐振风险。因此，经过校验RBDF可以选定为0.10 p.u.和0.20 p.u.。

表3 安装旁路阻尼滤波器后测试系统的谐振结构Table 3 Resonance structure of test system with BDF installed

另外，通过对比可以发现，在同一转子运行转速下，旁路阻尼滤波器电阻的选定值越大，则系统谐振模式的衰减因子越大，即谐振模式的稳定性越强，这表明滤波器电阻确实可以起到耗散扰动能量的效果。关于旁路阻尼滤波器电阻的取值，技术上来看其数值越大，则正电阻的补偿效果会越好，谐振风险越小，但如果电阻取值过大，对旁路阻尼滤波器和串补电容所形成的并联谐振频率点计算会存在影响。另外，鉴于旁路阻尼滤波器制造工艺，稳态运行下旁路阻尼滤波器也会存在一定的功率消耗，其工程应用取值需统筹经济方面来考虑。

4.3 仿真验证

为了验证旁路阻尼滤波器的谐振抑制效果，本文基于测试系统的仿真模型，对安装旁路阻尼滤波器后系统的运行情况进行了仿真测试，测试结果如图6 所示。图中区间1—4 分别对应ωm取值为1.2、1.1、0.9、0.8 p.u.。图6 表明，安装旁路阻尼滤波器后，测试系统仅在旁路阻尼滤波器电阻为0.05 p.u.且双馈风机运行于1.10 p.u.和1.20 p.u.的转子转速时会出现振荡现象，而在其他运行条件均可以稳定运行，验证了基于旁路阻尼滤波器谐振抑制措施的有效性。

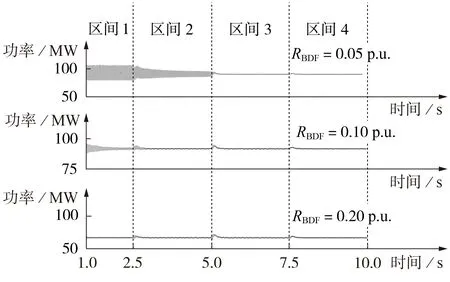
图6 安装旁路阻尼滤波器后双馈风电场输送功率的仿真波形Fig.6 Simulative waveforms of output power of DFIWG-based wind farm with BDF

需要说明的是，上述旁路阻尼滤波器主要针对单个不稳定的谐振模式设计，并不能保证适用于抑制其他振荡模态，存在一定的局限性。但对于双馈风电场的次同步振荡问题，其主要由双馈风机的负电阻效应所引起，本文所选取的不稳定谐振模式为算例分析结果中最不稳定的谐振模式，即此时双馈风机的负电阻效应最为显著，为此所设计的旁路阻尼滤波器对其他负电阻效应较弱情况下的谐振模式也具有一定的抑制效果。

5 结论

本文通过建立双馈风机的端口阻抗模型，并基于s域节点导纳矩阵法分析不同串补度和运行转速下双馈风电场经串补送出系统的网络谐振结构，提出了基于旁路阻尼滤波器的谐振抑制措施，最后，得出了以下几点结论。

1）通过电力网络谐振结构分析表明，在未安装旁路阻尼滤波器时，双馈风电场经串补送出系统确实存在一定的谐振风险。在同一线路串补度下，双馈风机的转子运行转速越小，系统谐振模式的衰减因子越小，系统的谐振风险越大；而在同一运行转速下，线路的串补度越高，系统的谐振风险越大。

2）通过电力网络谐振结构分析表明，在安装旁路阻尼滤波器后，双馈风电场经串补送出系统的谐振风险可以得到有效抑制；另外，旁路阻尼滤波器电阻的选定值越大，系统谐振模式的衰减因子越大，系统的谐振风险越小。

附录见本刊网络版（http：//www.epae.cn）。